
У р о к 16 (53).
Решение систем неравенств второй степени
с двумя переменными
Цель: формировать умение решать системы неравенств второй степени с двумя переменными.
Ход урока
I. Организационный момент.
II. Устная работа.
Является
ли решением системы неравенств 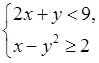 пара чисел:
пара чисел:
а) (5; –3); б) (3; 1); в) (–1; 2)?
III. Объяснение нового материала.
Сначала необходимо актуализировать знания учащихся о решении систем линейных неравенств с двумя переменными, а затем разобрать пример 1 из учебника.
IV. Формирование умений и навыков.
Упражнения:
1. Изобразите на координатной плоскости множество решений системы:
а)
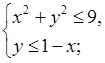 в)
в)
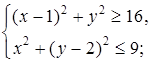
б)
 г)
г)
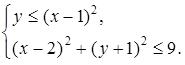
Р е ш е н и е
а)  б)
б)
в) 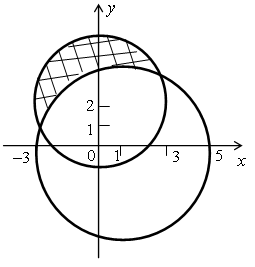 г)
г) 
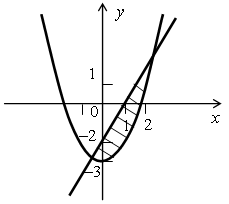
2. № 501 (а).
Р е ш е н и е
|
Изобразим на координатной плоскости множество решений этой системы, предварительно преобразовав ее:
|
|
Таким образом, множество решений этой системы неравенств задает треугольник ОАВ. Для нахождения его площади нужно знать высоту ВН, то есть абсциссу точки В. Точка В является точкой пересечения прямых у = х и у = 5 – х. Решим уравнение:
х = 5 – х;
2х = 5;
х = 2,5.
Значит, в треугольнике ОАВ АО = 5 и ВН = 2,5.
S = ![]() ∙ AO
∙ BH;
∙ AO
∙ BH;
S = ![]() ∙ 5
∙ 2,5 = 6,25.
∙ 5
∙ 2,5 = 6,25.
О т в е т: 6,25 ед2.
3. № 502 (б).
4. № 503.
Р е ш е н и е
Построим искомый угол:
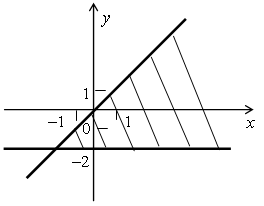
Получим
систему неравенств: 
Сильным в учебе учащимся можно предложить дополнительно выполнить несколько номеров.
1. № 577 (а).
Р е ш е н и е
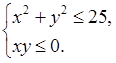
|
Неравенство х2 + у2 ≤ 25 задает круг с центром в начале координат и радиусом 5. Неравенство ху ≤ 0 задает вторую и четвертую координатные четверти. На рисунке показано множество решений этой системы неравенств: |
|
2. № 559 (б).
Р е ш е н и е
х (х2 – у) ≤ 0.
Произведение двух выражений будет отрицательным, если эти выражения имеют разные знаки. То есть это неравенство равносильно совокупности двух систем:

Изобразим на координатной плоскости множества решений каждой из систем:

V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется решением неравенства с двумя переменными?
– Что называется решением системы неравенств с двумя переменными?
– Как решаются неравенства с двумя переменными?
– Как решаются системы неравенств с двумя переменными?
Домашнее задание: № 500 (б, г), № 501 (б), № 502 (а).
Д о п о л н и т е л ь н о: № 557 (б).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.