Поделиться
43. Самостоятельная работа по теме Выполнение макетов геометрических тел.doc
Самостоятельная работа 1.2
Выполнение макетов геометрических тел
Цели выполнения:
- развитие графического представления пространственных образов;
- приобретение навыков выполнения и компоновки чертежа;
- освоение правильного выполнения линий чертежа по ГОСТ 2.303-68.
Время выполнения: 3 часа
Содержание:
На листе формата А3 или А2 без рамки и основной надписи выполнить развертку геометрического тела в соответствии с вариантом задания. Вырезать развертку и склеивать макет не обязательно.
Таблица 1 - Варианты выполнения самостоятельной работы 2.1
|
№ варианта |
Геометрическое тело, развертку которого необходимо выполнить |
Размеры: H — высота тела, D — диаметр основания. |
|
1 |
Конус |
H – 150 мм, D – 80 мм. |
|
2 |
Цилиндр |
H – 150 мм, D – 80 мм. |
|
3 |
Правильная прямая трехгранная пирамида |
H – 150 мм, D – 80 мм. |
|
4 |
Правильная прямая трехгранная пирамида |
H – 150 мм, D – 80 мм. |
|
5 |
Правильная прямая четырехгранная пирамида |
H – 150 мм, D – 80 мм. |
|
6 |
Правильная прямая пятигранная пирамида |
H – 150 мм, D – 80 мм. |
|
7 |
Правильная прямая шестигранная пирамида |
H – 150 мм, D – 80 мм. |
|
8 |
Правильная прямая трехгранная призма |
H – 150 мм, D – 80 мм. |
|
9 |
Правильная прямая пятигранная призма |
H – 150 мм, D – 80 мм. |
|
10 |
Правильная прямая шестигранная призма |
H – 150 мм, D – 80 мм. |
Рекомендации по выполнению:
- по учебнику проработать разделы «Развертка поверхностей геометрических тел» и «Многогранники, тела вращения», изучить теоретическую часть работы, данную ниже;
- скомпоновать чертеж по примеру выполнения работы (см. рисунки 1 - 5), проставить размеры;
- выполнить обводку линиями, установленными ГОСТ 2.303-68.
При проведении центровых линий внутри окружности необходимо помнить, что они должны обязательно пересекаться штрихами, а не точками. Штрихи должны выходить за пределы окружности на 3-4 мм. Штрихпунктирная линия должна заканчиваться штрихом, а не точкой.
Развертки поверхностей геометрических тел
Разверткой поверхности геометрического тела называется плоская фигура, которая получается в результате совмещения всех граней или всех поверхностей, ограничивающих тело, с одной плоскостью. Поверхности некоторых геометрических тел криволинейной формы, например шара и других поверхностей вращения, нельзя развернуть в одну плоскость. Для развертки таких поверхностей используют способы приближенной развертки.
Развертка призмы
На рисунке 1, а изображена правильная прямая трехгранная призма. Боковая поверхность призмы состоит из трех равных прямоугольников, ширина и высота которых известны. Основания призмы проецируются на горизонтальную плоскость проекций в истинную величину.
Построим развертку боковой поверхности
призмы (рисунок 1, б). Для этого вдоль горизонтальной прямой отложим три
отрезка, равных стороне основания призмы
.
Из точек 
проведем вертикальные прямые,
равные высоте призмы. Через полученные точки проведем горизонтальную прямую.
Полученная фигура — прямоугольник, состоящий из трех прямоугольников, которые
равны граням призмы, будет разверткой ее боковой поверхности. Совместим два
основания призмы — равносторонние треугольники с разверткой боковой поверхности
призмы. Пользуясь размером l, взятым с горизонтальной проекции призмы, и
линией связи, построим на развертке точку Е, принадлежащую грани 
.
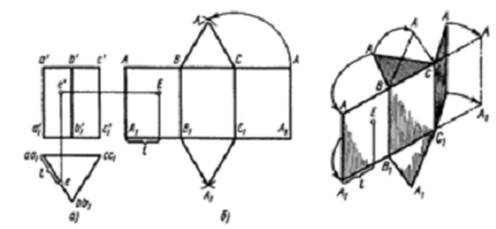
Рисунок 1 – Развертка поверхности призмы:
а) чертеж; б) полная развертка поверхности
Развертка пирамиды
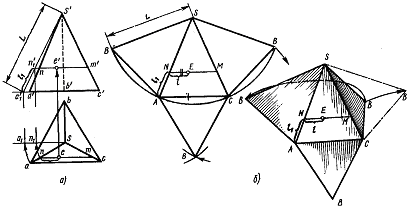
Рисунок 2 – Развертка поверхности пирамиды:
а) чертеж; б) полная развертка поверхности
Развертка цилиндра
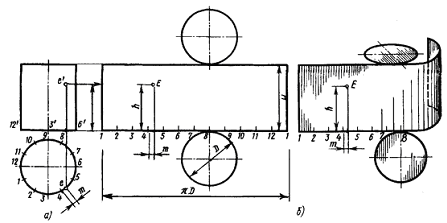
Рисунок 3 – Развертка поверхности цилиндра:
а) чертеж; б) полная развертка поверхности
Развертка конуса
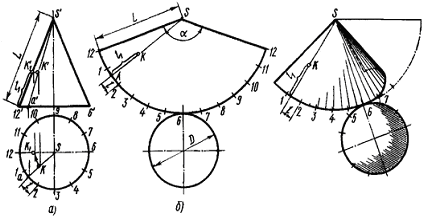
Рисунок 4 – Развертка поверхности конуса:
а) чертеж; б) полная развертка поверхности
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
