Сатья на тему: " Об одном нелинейном уравнении, которое сводится к уравнению Даламбера"

об одном нелинейном уравнении, которое сводится к уравнению даламбера

Гаджимирзаев М.М.,

учитель математики РЦДОДИ.

E-mail: [email protected]

Аннотация. В работе рассматривается уравнение, возникающее при описании различных процессов, связанных с передачей тепла. Это уравнение путем соответствующей замены удалось свести к хорошо изученному уравнению Даламбера. Кроме того, рассмотрена задача Коши для упомянутого выше уравнения.

Ключевые слова: уравнение Даламбера, задача Коши.

1.     Введение

Дифференциальные уравнения в частных производных являются математическими моделями задач, описывающих физические процессы. Именно поэтому они получили название уравнений математической физики (см., например, [1,2]).

  Моделирование колебательных процессов приводит к уравнениям гиперболического типа, простейшим из которых является уравнение колебания струны или, как часто принято говорить, уравнение Даламбера [1]

В настоящей работе рассматривается уравнение, возникающее при описании различных процессов, связанных с передачей тепла. Это уравнение путем соответствующей замены удалось свести к хорошо изученному уравнению Даламбера. Кроме того, рассмотрена задачи Коши для упомянутого выше уравнения.

2.     Уравнение, сводимое к уравнению Даламбера

Математическое описание многочисленных явлений и процессов естественных наук, так или иначе связанных с передачей тепла, дает уравнение

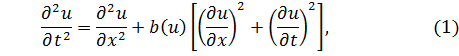
где   заданная функция.

          Отметим, что уравнения  нелинейное. Будем считать его уравнением нелинейной теплопроводности.  Задача состоит в его исследовании. С этой целью для заданной интегрируемой функции  рассмотрим отличную от нуля функцию

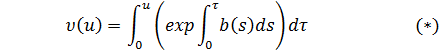
Имеем

,       (2)

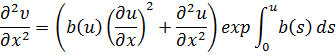
                                                (3)

Умножая обе части равенства (1) на функцию 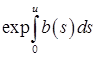, получим:

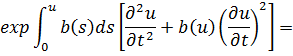
                    .           (4)

В силу (2), (3) не трудно заметить, что (4) можно переписать в виде:

                                                                            (5)

Последнее означает, что уравнение (1) посредством замены (*) сводится к уравнению Даламбера (5).

3.     Задача Коши

В этом пункте рассмотрим задачу Коши для уравнения (1), которое состоит в нахождении решения  уравнения (1), удовлетворяющее начальным условиям

 ,          (6)

(при она решена в главе 1 §1).

Подставляя в равенство (*) условие (6), получим:

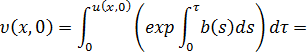
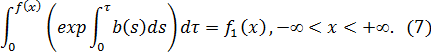
Из (*) имеем

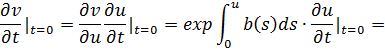
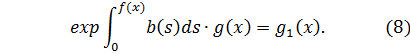
Таким образом, мы получили, что задача (1), (6) эквивалентно задаче (5), (7), (8). А задача (5), (7), (8) имеет следующее решение

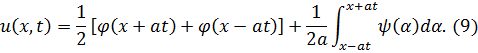
Заменяя левую часть (8) согласно (*), и подставляя правую часть, вместо получим решение задачи Коши (1), (6) в неявном виде:     

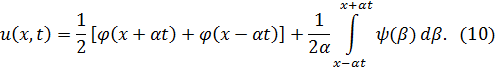
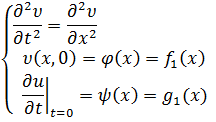
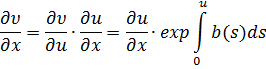
Заметим, что если левая часть (9) разрешима относительно ,  то эта формула дает явное решение задачи (1), (6).

Рассмотрим пример. Пусть , тогда взяв в (9) вместо нуля в нижнем пределе интегрирования внутреннего интеграла  степени единицу, и осуществив интегрирование, будем иметь: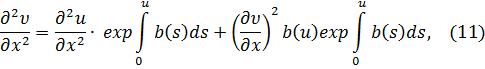      

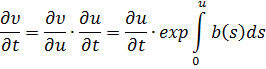
или

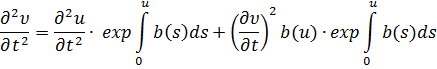
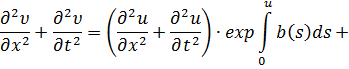
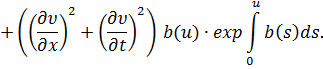
Извлекая корень от обеих части (11) и взяв его арифметическое значение, получим положительное решение задачи Коши в явном виде:

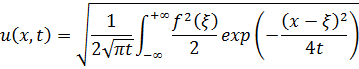
Рассмотрим случай, когда . Очевидно, что можно считать. При этом вместо (10) получим

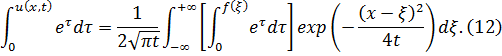
В результате интегрирование вместо (12) будем иметь

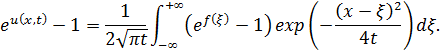
Откуда снова получаем явной выражение решения задачи Коши (1), (6):

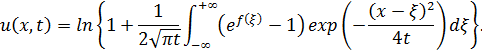
Библиографический список.

1.     Тихонов А. Н., Самарский А. А. Уравнения математической физики. 7-е изд. - М.: Изд-во МГУ: Наука, 2004. - 798 с.

2.     Мизохата C. Теория уравнений с частными производными. - М.: Мир, 1977. - 504 с.