Сатья на тему: "Умножение вектора на число"

УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО. СВОЙСТВА

 

Произведением ненулевого вектора  и  на число k называется такой вектор , длина которого равна , причем векторы  и  соноправлены при k>=0 и противоположно направлены при k<0. Произведением ненулевого вектора на любое число считается ненулевой вектор.

Произведение вектора  на число k обозначается так: k*.

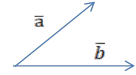
На рисунке изображены вектор  и векторы 3*,  -1,5*.

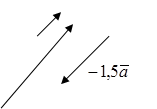     Из определения произведения вектора на число непосредственно следует, что:

произведение любого вектора на нуль есть нулевой вектор;

для любого числа k и любого вектора векторы  и k* коллинеарны

Умножение вектора на число обладает следующими основными свойствами (для любых чисел k, l и любых векторов , ) :

1)     

2) Для любых чисел α и β и для любого вектора :

3) Для любого числа α и для любых векторов  и : 

4) Для любых чисел α и β и для любого : (α+β)= α+β 

Теорема: Для того, чтобы  был каллениарен ненулевому вектору необходимо и достаточно, чтобы существовало такое число α, что   

Доказательство. (Необходимость).

Дано, что . Требуется доказать, что существует α, что  

а) допустим, что  .

Рассмотрим следующие векторы и

Эти векторы равны между собой т.к.

,   ,

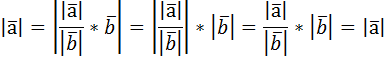
 , тогда ,,

Достаточность.

Для векторов выполняется . Требуется доказать, что они  .

Теорема. Доказательство достаточности следует из определения умножения вектора на число.

Данная теорема является основной теоремой для изучения аналитической геометрии.

   Данная теорема является основной теоремой для изучения аналитической геометрии.

 

     Линейная зависимость векторов.

Определение 1. Всякое множество (конечное или бесконечное) векторов называется система векторов

₁,₂,₃,₄,…_n –система векторов.

 Определение 2. Вектор  определенный  ₁* ₁ + ₂*₂+ ₃*₃ + ₄*₄+… + _n*+_n

Где  ₁,  ₂,  ₃,  ₄,…,  _n – действительные числа называется линейной комбинацией векторов ₁,₂,₃,₄,…_n

Пример:  5* ₁ -3 *₂+*₃ +0*₄ – линейная комбинация векторов.

Линейная комбинация векторов ₁,₂,₃,₄,…_n называется тривиальным, если все лямбда равны нулю  ₁= ₂= ₃= ₄=… = _n=0, то есть

0* ₁ +0*₂+0*₃ +0*₄+… +0*+_n называется тривиальной комбинацией.

Определение 3. Система векторов  ₁,₂,₃,₄,…_n называется линейно зависимой, если существует действительные числа  ₁,  ₂,  ₃,  ₄,…,  _n не равные одновременно нулю, что выполняется равенство

 ₁* ₁ + ₂*₂+ ₃*₃ + ₄*₄+… + _n*+_n=0

в противном случае система векторов  ₁,₂,₃,₄,…_n называется линейно независимой, т.е. равенство

 ₁* ₁ + ₂*₂+ ₃*₃ + ₄*₄+… + _n*+_n=0 выполняется лишь тогда, когда все лямбда равны нулю.

Пример:

рассмотрим, умножим  –линейно зависима.

  –линейно независима

Если α* ₁ +β*₂ то в этом случае говорят, что  линейно выражается через векторы ₁ и ₂. Таким образом, если задано равенство

  ₁* ₁ + ₂*₂+ ₃*₃ + ₄*₄+… + _n*+_n т.е. линейную комбинацию векторов ₁,₂,₃,₄,…_n  то вектор   линейно выражается через векторы ₁,₂,₃,₄,…_n .

Примеры:

 3* ₁ +4*₂

0* ₁ +0*₂.

 * ₁ + *₂+*₃

Теорема1.  Если система а линейно зависима, то хотя бы один из векторов линейно выражается через остальные.

Доказательство:  пусть ₁,₂,₃,₄,…_n –линейно зависима,

 ₁* ₁ + ₂*₂+ ₃*₃ + ₄*₄+… + _n*+_n=0               _i≠0

 ₁* ₁ + ₂*₂+ ₃*₃ + ₄*₄+… + _n*+_n=- _i* _i.       _i=-.

Последнее равенство означает, что _i  линейно выражается через остальные.

Теорема2: если система векторов ₁,₂,₃,₄,…_n содержит  вектор, то эта система линейна зависима.

Теорема3: если часть системы векторов линейно зависима, то вся система линейно зависима.

 

 

 

Векторное пространство.

I.Одномерное векторное пространство.

Множество всех векторов принадлежащих одной ко второй можно назвать одномерным векторным пространством.

V₁ –векторная одномерность.

 

 

, α÷(-∞;+∞).

Пусть  ненулевой произвольный вектор. Тогда множество векторов вида, где α –пробегает значение на (-∞;+∞) есть одномерное векторное подпространство, натянутое на .

Пусть V₁ –одномерное векторное подпространство. Любой  вектор из этого пространства называется базисом этого подпространства.

 

Любой  принадлежащий  коллениарен вектору , поэтому  .

В этом случае  линейно выражается через  и при этом число α –называется координатой вектора  относительно вектора .

 

           II. Двумерное векторное подпространство.

Множество всех векторов, лежащих, на обеих плоскостях можно называть двумерным вектором подпространства, обозначается  через .

 

Определение. Упорядоченную пару неколлениарных векторов называют базисом двумерного векторного подпространства.  Эта пара неколлениарны, и можно

 назвать их  базисом.

     

Обычно базис в   обозначают другим образом. , –базис.

В общем этот базис называется аффинным.

Если . , и если ., то базис называется прямоугольным, декантами. В геометрии такой базис обозначают через  .

Теорема. Пусть , –базис двумерного векторного пространства, тогда любой вектор двумерного подпространства единственным образом линейно выражается через базисные векторы (,).

Доказательство.

 

 

 

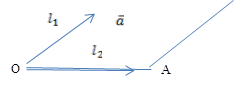
  –коллениарен.  –коллениарен .

Таким образом каждый вектор из линейно выражается через и .

 

Докажем единственность.

Пусть имеет еще одно разложение

.

Тогда 0. Из того, что  и  линейно независимы, следует

  -это единственность.

Если  линейно выражается ,  –называются координатами вектора  относительно  и .

В таком случае  называются координатами вектора относительно базиса  и .

 –первая координата вектора

– вторая координата вектора

В дальнейшем координаты вектора  будем обозначать таким образом: .

 

 

 

 

 

                                               

 

Пример.

 

 

 

 

 

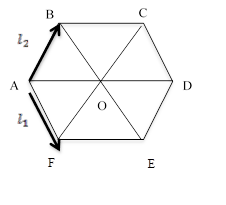
Выразить   и .

. 

. 

.  

      4..  

 

         Длина вектора

Определим длину вектора, зная координаты вектора. Рассмотрим декартово-прямоугольный базис.  

 

 

 

 

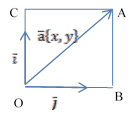
∆AOB –прямоугольный

 

Пример:

  

           Координаты.

Пусть V₂ двумерное векторное подпространство.  и  –базис V₂.

 

Найти координаты вектора

 

 

  

 

Если векторы складываются по соотношению координаты этих векторов складываются.

Пример:

  

 

 

Теорема: Пусть   относительно  и

 

      Доказательство.

 Необходимость.

Пусть требуется доказать

 на основе единственно или , то ,

 

 

 

Достаточность:

 

Требуется доказать .

 

 

 

Требуется найти координаты вектора.

 

Таким образом координаты комбинации векторов равно линейной комбинации соотносящих координатой векторов

Ориентация плоскости. Угол между ними.

 

 

 

 

 

 

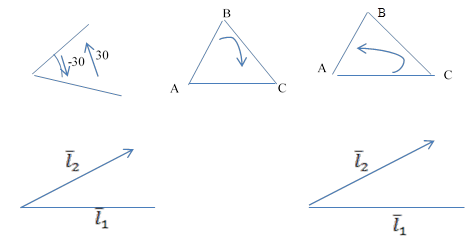Таким образом обход плоскости (двумерного вентерного подпространства) можно проделать либо по часовой стрелке, либо против часовой стрелки.

Других обходов нет.

Ели принять обход против часовой стрелки, то такой подход будет считать положительным, а по часовой стрелке считаться отрицательным.

Таким образом называется ориентировочной  если в ней указано направление обхода за положительным.

Ориентация плоскости можно задать либо треугольником, либо окружностью.

 

 

 

 

 

 

 

 

 

 

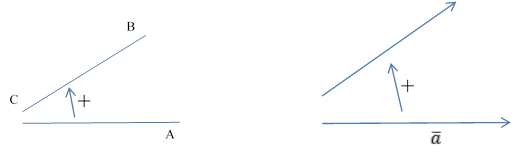Если заданы векторы  (- первый вектор,  –второй вектор) в случае ориентации против часовой стрелки считается угол поворота вектора , до совпадения с направлением вектора , при этом этот угол считается положительным.

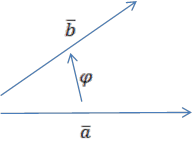
Угол между векторами будем обозначать

 

 

 

Поскольку угол, между  бесконечное множество в дальнейшем мы будем считать угол между векторами

 

 

 

 

 

 

 

 

Учитель математики ГКОУ РД «РЦДОДИ»     Гаджимирзаев М.М.