Сборник дилактических игр по математике для учащихся 5 классов

Система дидактических игр для учащихся 5-х классов.

Игра №1

Кроссворд

Тема: Повторение пройденного в начальной школе

Цель: повторить материал начальной школы, выявить пробелы в знаниях.

Содержание игры:

Учащимся предлагается разгадать числовой кроссворд, ответы которого являются решения данных заданий.

По вертикали:

1. 1260-120:2    (1200)

2. 4000000+70000+8000+600+5  (4078605)

3. 6000+7000+300+50+9  (67359)

4. 8000+600+1  (8601)

8. 624+367  (1021)

10. Один комбайнер намолотил 231 т зерна, а второй на 46 т меньше. Сколько зефира намолотили оба комбайнера?  (416 т)

По горизонтали:

1. Число, следующее за числом 99  (100)

5. 900000+3000+700+20  (903720)

6. Число, предшествующее числу 1200  (1199)

7. Число на один больше числа 8999 (9000)

9. 258·8  (2064)

11. Масса яблока 140 г, а масса груши на 60 г больше. Какова масса трех таких яблок и груши. (620)

Игра №2

Наша математическая игра

Тема: «Натуральные числа»

Цель: закрепить знания по теме

Содержание игры:

Ученики делятся на три команды. Им раздаются листы с заданиями. Все работают в команде, помогая и подсказывая друг другу. Кто первый решает, поднимает руку, и этой команде начисляется два балла, остальным по одному.

Всё решение один человек из команды записывает подробно и аккуратно на двойном листе, затем в конце игры сдает учителю. Все задания решаются последовательно, нельзя перескакивать задания не решив предыдущее.

В конце игры учитель проверяет работы учащихся и за неаккуратность и ошибки может снизить баллы команде. За подглядывание к другой команде и плохую дисциплину баллы снижаются.

Выигравшая команда получает медальки. После поздравлений учитель анализирует работы и говорит оценки.

Варианты заданий.

Каждой команде раздается свой вариант, но задания аналогичны друг другу.

Вариант 1

1.     Запишите цифрами числа

1)    Шесть тысяч восемьдесят пять

2)    Одиннадцать миллионов двадцать четыре тысячи девять

2.     Запишите все  трехзначные числа, для записи которых употребляются только цифры 5 и 3

3.     Нарисуйте шестиугольник, обозначите его, запишите  вершины и стороны измерьте отрезки, соединяющие противоположные вершины.

4.     Выразите

1)    9 дм 6 см в сантиметрах

2)    4567 м в километрах

3)    3т100 кг в килограммах

4)    7560 кг в тоннах, центнерах килограммах

5.     Нарисуйте 4 пересекающихся прямых и обозначите их, а так же точку их пересечения. От точки пересечения отложите отрезки на лучах по 3 см и обозначите их. Соедините полученные точки, какую фигуру вы получили?

6.     Обозначьте прямые и с помощью линейки найдите на рисунке точки пересечения прямых

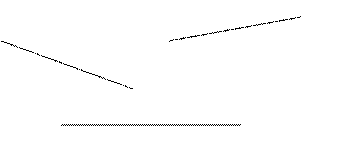
7.     Начертите координатный луч с единичным отрезком равным 20 мм, отметьте на нем А(3), В(5), С(6). Измерьте отрезки АВ, ВС, АС и расположите их в порядке возрастания.

8.     Запишите с помощью двойного неравенства

Число 10 больше, чем 5, и меньше, чем 15

9.     Сравните числа

1)    50107 и 50004

2)    6582185 и 6582184

Вариант 2

1.     Запишите цифрами числа

1)    Восемьдесят тысяч четыреста

2)    Три миллиарда сто тринадцать тысяч сорок

2.     Запишите все  трехзначные числа, для записи которых употребляются только цифры 6 и 7

3.     Нарисуйте пятиугольник, обозначите его, запишите  вершины и стороны измерьте отрезки, соединяющие противоположные вершины

4.     Выразите

1)    5 дм 1 см сантиметрах

2)    5070 м в километрах

3)    4т 20 кг в килограммах

4)    9564 кг в тоннах, центнерах и килограммах

5.     Нарисуйте 3 пересекающихся прямых и обозначите их, а так же точку их пересечения. От точки пересечения отложите отрезки на лучах по 4 см и обозначите их. Соедините полученные точки, какую фигуру вы получили?

6.     Обозначьте прямые и с помощью линейки найдите на рисунке точки пересечения прямых

7.     Начертите координатный луч с единичным отрезком равным 15 мм, отметьте на нем А(4), В(6), С(8). Измерьте отрезки АВ, ВС, АС и расположите их в порядке возрастания.

8.     Запишите с помощью двойного неравенства

Число 21 меньше, чем 28, а число 28 меньше, чем 45

9.     Сравните числа

1)    63001 и 63002

2)    3056809 и 3056810

Вариант 3

1.     Запишите цифрами числа

1)    Семьдесят семь тысяч сто восемь

2)    Сорок пять миллиардов три миллиона пять

2.     Запишите все  трехзначные числа, для записи которых употребляются только цифры 8 и 2

3.     Нарисуйте семиугольник, обозначите его, запишите  вершины и стороны, измерьте отрезки, соединяющие противоположные вершины

4.     Выразите

1)    11 дм 3 см сантиметрах

2)    15500 м в километрах

3)    1 т 3 ц в килограммах

4)    8745 кг в тоннах, центнерах и килограммах

5.     Обозначьте прямые и с помощью линейки найдите на рисунке точки пересечения прямых

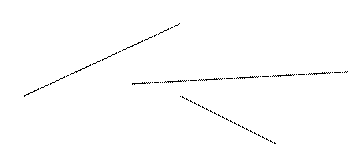
6.     Нарисуйте 5 пересекающихся прямых и обозначите их, а так же точку их пересечения. От точки пересечения отложите отрезки на лучах по 2 см и обозначите их. Соедините полученные точки, какую фигуру вы получили?

7.     Начертите координатный луч с единичным отрезком равным 10 мм, отметьте на нем А(5), В(7), С(9). Измерьте отрезки АВ, ВС, АС и расположите их в порядке возрастания.

8.     Запишите с помощью двойного неравенства

Число 21 меньше, чем 28, а число 28 меньше, чем 45

9.     Сравните числа

1)    41527 и 41638

2)    2085003 и 2086003

Игра №3

Путешествие в галактику Арифметики

Тема: Сложение и вычитание натуральных чисел

Цель: обобщить и систематизировать знания и умения по теме

Содержание игры:

Каждый ученик вешает себе на грудь бейдж с именем известного космонавта, которые дает им учитель. На доске нарисованы четыре планеты: Земля, Сложение, Вычитание, Геометрические фигуры. Чтобы попасть на планету, ученикам нужно ответить на теоретические вопросы, а на самой планете решить задачи.

После прохождения заданий планета дает свой символ и дарит ученикам свои знания. Получив все символы и знания, дети будут готовы к контрольной работе.

Итак, мы отправляемся в путешествие. Наш космический корабль улетает с планеты Земля и держит курс на планету Сложение.

Вот мы и на первой планете – Сложение. Её жители говорят, что впустят нас если мы скажем, что такое сложение и расскажем его свойства.

(Ученики отвечают определение сложения и его свойства.)

Молодцы, нас впустили на планету. Здесь на равнинах живет народ Слагаемое, а в море народ Сумма. Мы приземляемся и нас встречает народ Слагаемое, они и предлагают нам решить следующие задания.

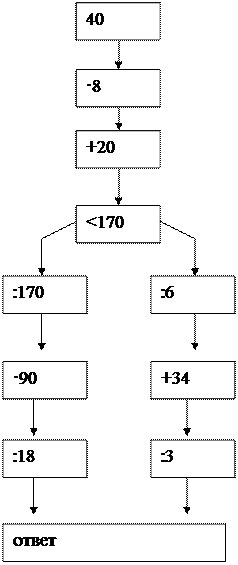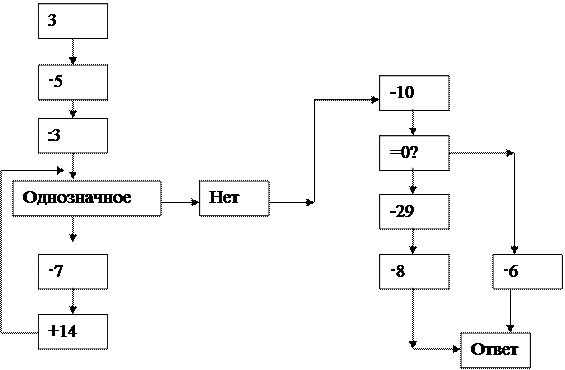
1. Вычислите устно:

а)                                                                          б)

 Да                                      Нет

    +50                                 ·8                                          Нет                                    Да

    :4                              +440

 -29                                 :10

Ответ 100

 в)                                                                                                                   

                                                                                                           Ответ 10

                                                                                                                         Да

                                                                                          нет

             Да

                                           Ответ 160          

Молодцы, теперь мы отправляемся к народу Сумма. Этот народ предлагает нам решить следующие примеры.

Вычислите:

а) 981453762+60241783   (1041695545)

б) 90446764+956324  (91403088)

в) 526 кг 790 г+37 кг56г   (633 кг 846 г)

Мы ответили на все вопросы и народы этой планеты дарят нам символ «+». Но нам необходимо найти другие символы.

Отправляемся на другую планету Вычитание. Планета Вычитание состоит из гор с народом Вычитаемое, из океана Разности и на суше проживает народ Уменьшаемое.

Итак, чтобы попасть на планету необходимо ответить что такое вычитание, а также его свойства.

(Отвечают теорию)

Направляемся к горам Вычитаемое. Решаем задание.

Даны числа 382, 238, 283,832

а) расположите в порядке убывания

б) на сколько большее из этих чисел больше наименьшего

Отправляемся в океан Разности.

Вычислите

а) 684409674-56345609   (628064065)

б) 7000780-6789774   (211006)

в) 28м 35см-14 м3 см  (14м 32см)

Молодцы, вы верно ответили на все вопросы и нам дают символ «-».

Осталась последняя планета. В путь!

Жители планеты «Геометрические фигуры» Периметр хотят, чтобы мы рассказали, что такое периметр и предлагают нам решить следующие геометрические задачи

Задача №1

В треугольнике АВС, сторона АВ равна 54 см, ВС на 27 см больше АВ, Ас на 14 см больше ВС. Найдите периметр треугольника.

Задача №2

В четырехугольнике АВСD, сторона АВ равна ВС, сторона AD равна CD, сторона ВС равна 34 см. СD больше АВ на 12 см. найдите периметр четырехугольника.

Теперь планета нам дарит символ «шестиугольник». Собрав все три символа, мы можем сказать, что готовы к контрольной работе.

Игра №4

Страна чисел и букв

Тема: упрощение выражений Уравнение

Цель: закрепить знания по теме

Содержание игры:

Жили-были числа 1, 2, 3 и т.д. и звали их как? Натуральные.

Ни одно число не было похоже на другое: кто-то был худеньким, кто-то толстеньким, кто-то высоким, кто-то низким. Когда числа радовались и дружили, то складывались, а когда ссорились – отнимались, но всегда старались жить дружной семьей, по определенным правилам – свойствам. А каким? (Ученики отвечают свойства сложения и вычитания)

Как-то раз число 5 пошло гулять в сады скобок и плюсов и встретил там букву А. она была не похожа на его народ и сидела у реки и плакала.

- Почему ты плачешь? – спросил 5

- Я заблудилась и не могу найти свою семью

- Пойдем со мной, мы тебя приютим.

5 и А отправились в город натуральных чисел. Там её накормили, согрели, а на следующий день взрослые числа 26,34,46 отправились на поиски её семьи. Им нужно будет пройти болото, зыбучие пески и вулкан. Помогите им дойти до города букв.

Посчитайте удобным способом

638+375+272

Упростите выражение к+527+293

Найдите значение выражение, предварительно упростив его.

49-(14+с)  при с=13

И вот наконец они дошли до города букв. Жители его были очень расстроены, ведь потеряли свою принцессу букву А. Тогда числа рассказали, что их принц число 5, нашел её и они приглашают букв в свой город и буквы с радостью согласились.

На обратном пути им пришлось проходить те же препятствия

Посчитайте удобным способом

623-(15+343)

Упростите выражение 456-(146+с)

Найдите значение выражение, предварительно упростив его.

43+(х+18) при х=19

Дойдя до города натуральных чисел, принцесса А кинулась к родителям, но она не хотела уходить из этого города, ведь принц и принцесса А полюбили друг друга. Числа и буквы, поговорив, решили сыграть свадьбу. Так появились буквенная запись свойств сложения и вычитания. Напишите их на доске.

На свадьбе все веселились и решали уравнения

а) 18+у=41

б) х-23=41

в) (24-х)+37=49

г) 44+(а-85)=105

д) 69+(87-к)=103

Задача№1

На отрезке АВ равным 36 см отметим точку М, что АМ=14 см, и точку К, что ВК= 12см. найти МК

Вот и сказке конец.

Игра №5

Математический марафон

Тема: Арифметические действия и их свойства

Цель: обобщить и систематизировать знания и умения по теме.

Содержание игры:

Класс делится на три равные команды: Сложение, Вычитание, Умножение.

Учитель – ведущий в роли делении. Выбирается жюри, которое будет следить за подсчетом баллов, дисциплиной, оценивать команды. Выбираются капитаны команд, которые будут участвовать в отдельном конкурсе.

1 конкурс.             

Чтобы решить, кто начинает первым, нужно ответить на вопросы:

1) Сформировать сочетательное свойство умножения

Решаем, какая команда будет второй.

2) Сформулировать переместительное свойство умножения.

Решаем кроссворд «Птичка»

Команды отвечают по очереди, если ответа нет или он неверен, то ход переходит другой команде. За угаданное слово начисляется по баллу.

По горизонтали.

2. Результат деления

5. Прибавление к числу 5 три раза 1

6. действие, с помощью которого по произведению и одному множителю, находят другой множитель.

8. число при сложении

11. числа, которые складывают

По вертикали

1. действие, с помощью которого по сумме и одному слагаемому находят другое слагаемое.

3.что значит найти сумму n слагаемых каждое их которых равно m

4.число, получившееся при делении с остатком

7.числа, которые перемножают

9.число, из которого вычитают

10. результат вычитания

12. число, которое делят

13. число, на которое делят.

Подводим итоги конкурса.

2 конкурс.

Командам раздаются листочки с алфавитом и его нумерацией. Необходимо будет найти корни уравнений и по ним найти в таблице букву и составить слово. Корень уравнения соответствует номеру в таблице, а номер букве.

Задание на скорость, кто первый -3 балла, второй - 2 балла

А

Б

В

Г

Д

Е

Ё

Ж

З

И

Й

1           2            3        4           5           6         7            8         9           10        11

К

Л

М

Н

О

П

Р

С

Т

У

Ф

 12        13        14        15         16        17        18         19        20        21       22

Х

Ц

Ч

Ш

Щ

Ъ

Ы

Ь

Э

Ю

Я

23         24        25         26        27         28       29         30         31       32         33

1-я команда

15·а=15:а

у-6=8

у:7=3

17+7=31

28-у=9

2-я команда

(z+z)-z=z·z

х:4=3

14+х=30

Х-9=7

36-х=10

3-я команда

к·к+3=к+15

к·5=5

19+к=38

40-к=28

к:13=1

Подводим итоги конкурса и оцениваем.

Что же мы вспомнили в данных упражнениях? Как решают уравнение? Как узнать, верно ли мы решили уравнение?

3 конкурс

Конкурс капитанов. Пока капитаны решают, остальные участники выполняют другое задание.

Задание для капитанов

Найти значение выражения

к:19-95 если к=5719.

Является ли число 5749 корнем уравнения к:19-95=206

Задание для остальных участников игры.

Составить интересную задачу по уравнению 120-х=45.

Жюри оценивает. Максимум 3 балла.

Подводим итоги конкурса капитанов и команд

 4 конкурс.

Угадать слово на скорость. 2 балла

Задания

1)    Выполнить деление 139169 на 45

2)    Найти делимое, если неполное частное 25, делитель 8, остаток 5.

3)    Вычислить периметр прямоугольника, если длина его 50 см, ширина 6 дм.

4)    Расположите в порядке убывания3+17; 39-9; 11+5

5)    Найдите закономерность и продолжите 1,3,5……

Подводим итоги конкурса.

5 конкурс.

Решить задачу. 3 балла

1 команда

Велосипедист ехал 2 часа с некоторой скоростью, после того как он пройдет еще 4 км, его путь будет равен 30 км. Найти его скорость.

2 команда

Велосипедист ехал 4 часа с некоторой скоростью, после того как он пройдет еще 10 км, его путь будет равен 90 км. Найти его скорость.

3 команда

Велосипедист ехал 3 часа с некоторой скоростью, после того как он пройдет еще 12 км, его путь будет равен 132 км. Найти его скорость.

Подводим итоги конкурса. Подведение итогов всей игры. Если команды набирают одинаковое количество баллов, то им предлагается придумать свой девиз или еще какое-нибудь творческое задание, которое оценивается жюри. В конце игры награждение победителей грамотами.

Игра №6

Отгадай стихотворение

Тема: Упрощение выражений

Цель: закрепить знания по теме

Содержание игры:

Как нету на свете

Без ножек столов,

Как нету на свете без рожек козлов,

Котов без усов

И без панцирей раков,

Так нет в арифметике

Действий без знаков.

1. Мы изучали упрощенье

И был закон такой простой

С ним делали перемещенье

И радовались игрой.

а) 618·24+618·76

б) 618·34-518·34

в) (250+71)·4

2. Мы по порядку выполняли

В примерах действия не раз

Их правила мы узнавали

И возводили в степень. Класс!

а) 56+(111-505:5)·3+42:3

б) (3·6)²:9-2·4²

в) упростить выражение

31а+127+48а, при а=10

3. Как интересны уравненья,

И как их корень находить,

Используя ль распределенье,

Или возможно, упростить

а) 17х-4х=195, 5х+23х=168

б) в двух бригадах 87 человек. В первой бригаде в два раза меньше людей, чем во второй. Сколько человек в каждой бригаде?

в) Задача очень не проста

Найти не каждый сможет,

Чему равняется звезда,

Велосипед и ёжик

 **7

 **4

 6**

___

1*03

г) Чему равняется ракета,

сказать ты можешь или нет?

Билет на Марс, но у билета

Есть свой космический секрет

 14**

 *6*1

 **46

 484*

1*25*

4. а)

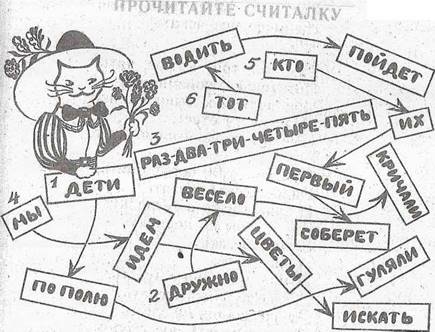
(Дети по полю, гуляли,

Дружно, весело кричали:

«Раз, два, три, четыре, пять!

Мы идем цветы искать:

Кто их первый соберет,

Тот водить пойдет)

б) Как записать число 10 четырьмя различными цифрами, соединив их знаками действий?

в) Найди в таблице числа по порядку от 26 до 50

г) Из разных цифр, я сделала бусы,

А в тех кружках, где чисел нет,

Р ассавье минусы и плюсы,

Чтоб данный получить ответ.

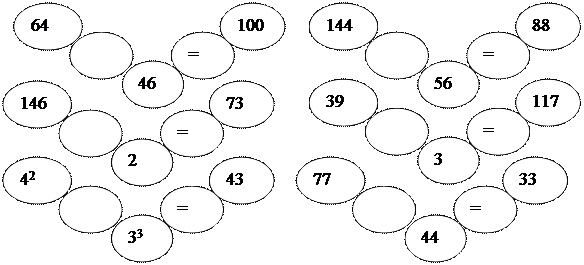
В конце получается стих:

Упрощать мы научились,

Икс умеем находить,

В степень мы навозводились,

Знаем, можем мы учить!

Игра №7

Наш дом

Тема: Площади, Объемы

Цель: закрепить полученные знания, откорректировать знания по теме

Содержание игры:

Сегодня мы с вами поедем за город и будем там строить дом.

И прежде чем мы поедем, нужно посчитать, сколько мы потратим денег.

Итак цены:

Участок стоит 10³ руб.

Пол  5² руб

Стены 4·36 руб

Потолок 8²-38

Крыша 120:4 руб

Окна 85 руб

Дверь 16 руб

Составим выражение и найдем его значение.

10³+5²+4·36+(8²-38)+120:4 +85+16

По скольку мы должны скинуться? Нас 25, и я 26

1326:26=51 руб

Кто первым посчитает выражение, тот будет хранителем денег.

Теперь найдем нам шофёра, который нас всех повезет.

Нам нужно проехать 240 км, со скоростью 80 км/ч.сколько времени нам понадобиться чтобы доехать до нужного места?

Кто быстрее посчитает, тот и будет шофером..

Ну, поехали!

Вот мы и на месте. Перед нами пустой участок земли. Что же хочется сделать с самого начала?

Поставить забор.

Итак длина нашего участка 30 м, а ширина 20 м. Какова же будет длина забора?

А какова же площадь нашего участка? Для чего нам её нужно найти?

Чтобы нечайно не построить дом больше, чем участок.

Сколько же у нас соток? 6 соток. Кто первым посчитал периметр, и площадь?

Теперь можно строить дом. Дом состоит из 6 плит в виде прямоугольников. В виде какой фигуры мы получили наш дом?

 В виде прямоугольного параллелепипеда.

Построим домик длиной 5 м, шириной 6 м и пусть будет 2 этажа высотой по 2 м каждая.

Какую площадь будет занимать наш дом? Кто первый ответит, отвечает за корпус дома.

А крыша нам нужна?

Она состоит из четырех одинаковых прямоугольных треугольников со стороной 4 см.

Какую площадь будет занимать крыша?

А окна нам нужны?

У нас 4 окна, квадратные. Их общая площадь 400 см², найдите сторону окна.

Кто первый посчитает – ответственный за окна.

А чего же нам еще не хватает? Двери.

Её измерения равны 1м. 2 м. найдите площадь двери и переведите её в см².

И вот мы и построили дом и теперь умеем находить площади и объемы.

Игра № 8

Холодное сердце принцессы

Тема: Обыкновенные дроби

Цель: закрепить полученные знания, откорректировать знания по теме

Содержание игры:

В одном красивом замке жила прекрасная принцесса, но она была заколдована злой колдуньей, и её сердце стало наполовину холодным. Принцесса ждала принца, который не приходил. Проходили года, дни, недели, а она все сидела у окна и ждала его. Тем временем её сердце становилось все холоднее и превратилось в лед.

Принцесса стала жестокой и злой и всех, кто приближался к замку превращала в лед. Но у неё было слабое место: она не могла превратить в лед умных и добрых людей.

Спустя три дня приехал принц, но принцесса не узнала его и не открыла ворота замка и чуть не погубила его.

Принц хоть и был очень добрым, но он был не очень умен, поэтому он написал в наш класс письмо, с просьбой помочь ему.

Вот мы подходим к воротам замка. Чтобы открыть их нужно 10 человек. Сила принца равна 2/5 этого количества, сколько еще ему нужно человек?

Ворота открылись и принц вошел в замок. Охрана не пропускает его, и просит отгадать загадку

Найдите значение выражения:

12/17-3/17-к при к=4/17

Охрану мы преодолели, но принцессы закрыла все двери, которые ведут в её комнату. Помогите принцу отгадать нужную дверь.

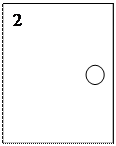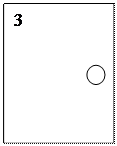Х+3/11-7/11=6/11                11+2/5-3-1/5=2+4/5           вот наша дверь

Принц вошел в комнату и увидел принцессу, она была очень хмурой и злой. Её лицо было белым, как снег, а глаза и губы прозрачными как лед.

Нужно растопить сердечко принцессы. Помогите принцу.

1. сердце красавица состоит из 45 льдинок, а 5/9 мы можем растопить нашей добрым сердцем. Сколько же льдинок мы сможем растопить?

2. осталось растопить 30 льдинок, 5/6 можно растопить добрым словом, а остальное само растает. Сколько льдинок сами растают?

Принцесса ожила. Её щеки порозовели, глаза снова стали голубыми. Она улыбнулась и обняла принца.

Принц не забывает о своих обещаниях и дарует мальчикам титул рыцаря, а девочкам – почетных дам королевства.

Игра № 9

Эстафета

Тема: Десятичные дроби

Цель: обобщить знания по теме десятичные дроби, устранить пробелы в знаниях.

Содержание игры:

Ученики делятся на три команды так, чтобы в каждой из них были и сильные и слабые ученики. Заранее командам предлагается придумать свое математическое название, связанное с десятичными дробями, а также свой девиз. Жюри оценивает творческую работу учащихся. Парты расположены так, чтобы во время эстафеты ученикам было легко выбегать к доске, а также чтобы они не столкнулись друг с другом. Учащиеся могут поддерживать своих друзей, но не кричать, за плохую дисциплину с команд снимаются баллы. Те, кто решает все первым получает два дополнительных балла к заданию. Как только одна из команд заканчивает конкурс, эстафета прекращается.

1 конкурс.

Перевести обыкновенные дроби в десятичные дроби.

1 команда

2 команда

3 команда

2 конкурс.

Заполнить пропуски. Задание выполняется всей командой на скорость.

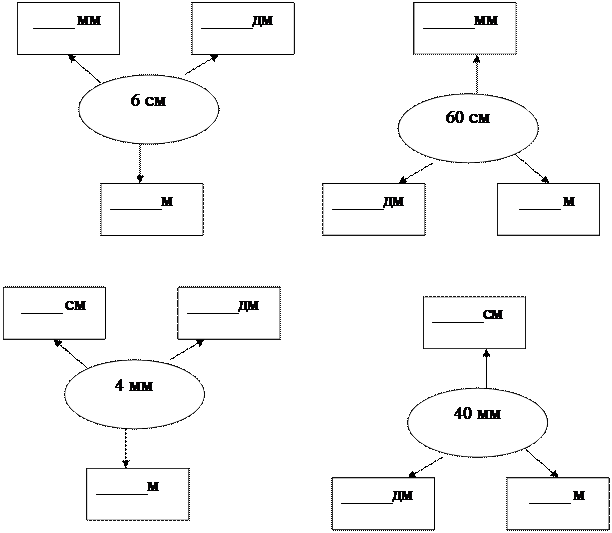
3 конкурс.

Сравнить дроби. Ученики выходят решать по очереди, соревнуясь с другими командами

1 команда

5,089 и 5,1

3,57 и 3,58

8,61 и 8,034

2 команда

0,64 и 6,35

7,25 и 7,3

3,29 и 3,3

3 команда

8,1 и 8,097

6,50 и 6,5

4,85 и 0,1

4 конкурс

Ученикам необходимо отгадать слово. Вывешивается плакат с буквами и числами, учитель диктует десятичную дробь, а ученики находят необходимое число и смотрят соответствующую букву и составляют слово.

Задание выполняется командами на скорость.

5 конкурс

Сложить дроби. Ученики выходят по очереди, соревнуясь.

1 команда

5,9+1,6

8,9+4

5,7+3,28

4,7-2,8

12,1-8,7

3-2,41

2 команда

8,3+0,8

13+4,2

2,58+1,4

5,1-4,7

45,6-1,9

17-0,87

3 команда

2,8+1,9

8+2,6

1,27+2,4

6,5-2,7

11,2-9,6

21-3,5

6 конкурс

Решить примеры и зачеркнуть буквы, которым соответствует ответ, из не зачеркнутых букв получится слово.

7,4+3,2

18,6+4,2

7,5-0,7

5,9+0,3

50,2-20,2

3-0,4

9,5-4,3

4,2+2,06

7 конкурс

Решить задачи на скорость у доски, выбирается один человек из команды.

1 команда

Найти скорость катера по течению и против течения, если его собственная скорость 18,6 км/ч, а скорость течения равна 2,4 км/ч.

2 команда

Найти скорость катера по течению и против течения, если его собственная скорость 30,5 км/ч, а скорость течения равна 2,8 км/ч.

3 команда

Найти скорость катера по течению и против течения, если его собственная скорость 40,9 км/ч, а скорость течения равна 3,15 км/ч.

8 конкурс.

Команде необходимо округлить десятичные дроби на скорость.

До десятых: 0,85; 4,78; 95,39

До сотых: 0,455; 9,326; 86,391

До целых: 354.854; 38,539; 1,16

Игра № 10

Скачки

Тема: Умножение и деление десятичных дробей на натуральные числа.

Цель: обобщить знания по теме десятичные дроби, устранить пробелы в знаниях.

Содержание игры:

Учитель выбирает из класса несколько групп по три человека в каждой, где необходимо учесть, что группа должна быть одного уровня знаний.

Начинается урок со слов «Сегодня у нас скачки! Прошу делать ставки!». Учитель раздает ученикам листочки:

После этого учитель объявляет участников первого заезда и каждый ученик напротив заезда ставит ту фамилию из этих трех, которую он считает выйгрышной. Далее аналогично с остальными заездами.

После этого учитель собирает листочки и говорит что приз достанется тому, кто правильно определит всех победителей и будет очень близок к этому.

1 заезд

На старт приглашаются участники первого заезда.

Найти значение выражения: 53,3:26+3,85·24

Кто первый решит из участников поднимает руку. Остальные в классе тоже решают пример для самопроверки.

2 заезд

Решить уравнение

(2,8-х):0,3=5

Остальные ученики тоже решают задание.

3 заезд.

Задача.

Пять машин песка и три машины щебня имеют массу 22,8 т. Найдите массу одной машины щебня, если масса одной машины песка равна 2,7 т.

Задача для зрителей.

4 пакета картофеля и три пакета моркови имеет массу 15,8 кг. Найдите массу одного пакета моркови, если масса пакета картофеля равна 2,6 кг.

4 заезд

Задача.

Найдите периметр квадрата со стороной 3,4 см.

Задача для зрителей.

Найдите сторону квадрата, если его периметр равен 34,1 см.

5 заезд

Решить уравнение.

124,2:(98-(8х+76,52))

Уравнение для зрителей.

166,4:(89-(17х+76,66))

Игра № 11

Экскурсия в Санкт-Петербург

Тема: Умножение и деление десятичных дробей, среднее арифметическое.

Цель: обобщить знания по теме десятичные дроби, устранить пробелы в знаниях.

Содержание игры:

Ребята сегодня мы отправляемся на экскурсию по нашей северной столице Санкт-Петербургу.

Когда мы отправляемся ехать куда-либо, то в первую очередь нам что необходимо купить?

Билеты.

Итак, едем на вокзал покупать билеты. Билет в Санкт-Петербург стоит 1534,86 руб. нас 25 человек и я сопровождающий, значит нас 26. Сколько же денег на понадобиться чтобы заплатить за все билеты?

1534,86·26=39906,36 руб.

Учитель раздает каждому ученику по билету.

Не забудьте сохранить билеты, иначе нам не будет скидки на обратный путь.

Мы садимся в поезд и он отправляется.

Задача №1

Первый участок пути поезд ехал 3,6 ч со скоростью 80 км/ч, а второй участок 7,9 ч со скоростью 95 км/ч. Найдите среднюю скорость, с которой ехал наш поезд.

(3,6·80+7,9·95):11,5=90,3 км/ч.

В пути учитель рассказывает о городе.

Санкт-Петербург - самый северный из числа крупнейших городов мира. Его географические координаты - 59°57' северной широты и 30°19' восточной долготы. Площадь города составляет 606 кв. км, а с пригородами -1439 кв. км.
Высокоширотным положением города объясняется явление белых ночей. Белые ночи наступают 25-26 мая, когда солнце опускается за горизонт не более чем на 9°, и вечерние сумерки практически сливаются с утренними. Наибольшая продолжительность дня приходится на 21-22 июня (18 ч. 53 мин.); заканчиваются белые ночи 16-17 июля. Продолжительность белых ночей в общей сложности более 50 дней.
Главная водная артерия города - река Нева. Свое название она получила от озера Нево (так в древности называлось Ладожское озеро), из которого берет начало. Длина Невы - 74 км (в городе - 32 км), средняя ширина реки в черте города около 600 м, глубина - до 24 м. Поверхность воды составляет десятую часть площади города.
Кроме Невы значительное влияние на формирование города оказывают многочисленные реки, протоки и каналы (их 53). Через них перекинуто 308 мостов (с учетом пригородных - мостов более 534). Среди них - 22 разводных. Общая длина всех мостов города - около 16 км. Самый длинный мост на Неве - мост Александра Невского (909 м, с учетом пандусов), самый широкий - Синий мост на реке Мойке (99, 5 м).
Город расположен на 47 островах Невской дельты. Самые большие из них - Васильевский и Петроградский.
Город нередко подвергается наводнениям. Чаще всего они бывают осенью, при ураганных западных ветрах. За все существование города Нева более 300 paз поднималась выше своего обычного уровня. Самое крупное наводнение случилось 7 ноября 1824 года, когда вода поднялась на 4, 1 м выше ординара. Последнее наводнение которое поставило в тупик всех гидрометеорологов и прогнозистов произошло 9 января 2005 года, вода зимой при ставшем льде Невы поднялась на 2,5 метра и подтопила город. Но это зрезвычайно редкое явление для зимнего периода.
Население Санкт-Петербурга составляет около 5 млн. человек.

Наконец мы приехали в город, разместились в гостинице и решили отдохнуть. Каждый из нас отдыхает в номере по 5 человек. Учитель говорит, кто в каком номер отдыхает. Ученики делятся на группы и рассаживаются по группам. Каждой группе будет предложено измерить площадь и объем своего номера.

1. а=4,1 м

b=2,8 м

c= 1,8 м

2. а= 3,4 м

b= 3,4 м

c= 1,8 м

3. а= 3,6 м

b= 4,2 м

c= 1,8 м

4. а= 5,2 м

b= 2,9 м

c=1,8 м

5. а= 4,8 м

b= 2,6

c=1,8 м

Ночью мы все хорошо поспали и отправились на завтрак. Посчитайте сумму, затраченную нами на каждого человека, найдя значение данного выражения.

(22-18,3)·6,6+3:0,6  (ответ 22,82 руб)

После завтрака мы отправляемся  на экскурсию по городу.

Чтобы узнать, куда мы отправляемся ученикам необходимо отгадать загадку.

Найдите среднее арифметическое чисел

35 и 6,5

5,2 и 4,8

4,6 и 9,23 и 2,1

4,12 и 7,95

46,3 и 95,8

756,4 и 12

Получили слово ОРЕШЕК, так называется одна из крепостей этого города.

Сначала мы приезжаем в Шлиссельбургскую крепость

Крепость была построена новгородцами в 14 веке. В 17 веке крепость в ходе длительной осады взяли шведы. Обратно крепость была отбита Петром в ходе Серверной войны. Взяв Нотебург ("орешек"), Петр повелел переименовать ее в Шлиссельбург ("город-ключ") - ключ, открывающий путь к дальнейшим победам в Северной войне и к Балтийскому морю. В дальнейшем в крепости содержали множество знаменитых политических преступников и террористов. Здесь сидели декабристы, народовольцы, а во дворе крепости вместе с другими террористами был казнен А.И. Ульянов (брат Ленина). Во время Великой Отечественной войны Шлиссельбургская крепость в течение почти 500 дней героически оборонялась и устояла, не допустив замыкания кольца блокады вокруг Ленинграда. Гарнизон крепости внес вклад и в освобождение города Шлиссельбурга, который в 1944 году был переименован в Петрокрепость. С 1966 года Шлиссельбургская крепость (Орешек) снова стала музеем.

Отправляемся в крепость Ивангород

Ивангородская крепость была построена в 1492 г. Иваном III для защиты от ливонских и шведских войск. Поэтому и место для ее возведения было выбрано не случайно: на берегу реки Наровы, прямо напротив рыцарского замка Нарвы. Вначале крепость была маленькая. Существует даже легенда о том, что была она построена на территории, опоясанной разрезанной на ленты лошадиной шкурой. Далее крепость расширялась и перестраивалась. Несколько раз и Нарва, и Ивангород переходили от нас к шведам и обратно. Только Петру I в ходе Северной войны - в 1704 г. - удалось вернуть России и Нарву и Ивангород. Во время Великой Отечественной войны крепость сильно пострадала от фашистов, взорвавших ее при отступлении, и от многочисленных обстрелов в ходе боев. Однако в данный момент крепость выглядит весьма величественно. Жаль только, что Нарвский замок уже так просто не посмотреть - нужна виза в Эстонию.

В обед мы заходим в магазин, чтобы купить что-нибудь перекусить. Продавец попросила нас посчитать среднее количество яблок в одном ящике и тогда она даст нам их бесплатно.

Задача №2

В магазин привезли 10 ящиков по 3,6 кг в одном и 40 ящиков яблок по 3,2 кг в одном. Сколько в среднем кг яблок в одном ящике?

(10·3,6+40·3,2):50     (ответ 3,28 кг)

Ближе к вечеру мы отправляемся на экскурсию в Александровский дворец.

На территории архитектурного ансамбля Царского Села, в северной части Александровского парка, среди живописных пейзажей стоит замечательный дворец с двухвековой историей. Это Александровский, или Новый, Царскосельский дворец. Он был заложен в 1792 году по распоряжению императрицы Екатерины II и приподнесен в дар к бракосочетанию её первого и любимого внука, великого князя Александра Павловича (будущего императора Александра I) с великой княжной Елизаветой Алексеевной (1779-1826). После революции 1905 года, Александровский дворец становится постоянной резиденцией императора Николая II , родившегося в Царском Селе. Именно в этом дворце прошли 22 года царствования последнего российского императора. Утром 1 августа 1917 года отсюда царская семья была отправлена в ссылку, в Тобольск.

Но вот пришло время уезжать. Мы прощаемся с городом и на вокзале покупаем билеты. За то что мы очень хорошо отвечали на вопросы экскурсоводов, нам делают скидку на обратные билеты. Итак, мальчикам скидка 20 %, а девочкам 21 %. Посчитайте, сколько всего мы потратим на обратные билеты.

Игра № 12

Математическое лото

Тема: Угол. Чертежный треугольник. Транспортир.

Цель: обобщить знания по теме десятичные дроби, устранить пробелы в знаниях.

Содержание игры:

На доске плакат с 20-ю номерами, под каждым номером написано имя ученика.

Учитель в коробку помещает листочки с номерами. Любой ученик вытаскивает листочек и читает написанный номер, а учитель снимает этот номер с плаката и читает имя ученика, который будет отвечать на вопрос. Ученик, который отвечает, после своего выступления, достает бумажку из коробки и говорит номер и т.д. в листочках может быть переход хода, а также номер-сюрприз, например в нашей игре ученик, который вытаскивает №20 получает оценку 5.

Задания к каждому номеру.

1)    Что такое угол? Что называют сторонами и вершиной угла. Выйти к доске, начертить и обозначить угол.

2)    Как определить, равны ли углы?

3)    Что такое развернутый угол, скольким градусам он равен?

4)    Что такое прямой угол, скольким градусам он равен?

5)    Постройте прямой угол с помощью чертежного треугольника.

6)    Для чего необходим транспортир? Как измерить угол с помощью транспортира.

7)    Что такое градус?

8)    Как построить угол с помощью транспортира?

9)    Что такое острый, тупой углы?

10)    Чему равна сумма углов в треугольнике?

11)    Что такое биссектриса? Начертить её на примере любого угла.

12)    Что такое круговая диаграмма?

13)    Постройте угол в 35⁰.

14)    Постройте угол в 184⁰.

15)    Начертите треугольник АВС, у которого угол А равен 100⁰. Измерьте остальные углы.

16)    Луч ОК делит прямой угол АОР на два угла. Угол АОК составляет 0,6 угла АОР. Найдите градусную меру угла КОР.

17)    Найти каждый их этих углов.

                       4х                     х

18)                                 С

                                               Р

              А

                                                 К

САК=40⁰. Найти углы АСР и рак, если АР – биссектриса

19)    Угол DKP – развернутый, КВ – биссектриса. Просели луч КМ так, что угол ВКМ равен 38⁰. Какой может быть градусная мера угла DKM?

20)    Оценка 5

Игра № 13

Лотерея

Тема: Действия с натуральными числами.

Цель: закрепить знания по теме

Содержание игры:

Ученики делятся на три команды (каждая команда садится на свой ряд). По два человека от команды должны разыграть лотерею: вытащить билет и ответить на него. Билет включает в себя теоретический материал по данной теме. В билете три вопроса. Если ученик отвечает на них правильно, то команда получает три балла, если затрудняется ответить, то просит помощи у своей команды, или же ход переходить другой команде.

1 конкурс.

Билеты к лотерее.

Билет №1.

а) Какие числа называются натуральными? Сколько цифр используют для написания чисел? Назовите эти цифры.

б) Как называются числа при умножении?

в) В каком порядке выполняются действия в выражении без скобок, если в нем встречаются только сложение и деление?

Билет №2.

а) Как называются числа при сложении? Может ли сумма быть равной одному из слагаемых?

б) Свойства умножения

в) Записать число 365057000606 на доске, почитать его и назвать классы.

Билет №3.

а) Как называются числа при вычитании?

Найти число а:  а+а=а-а

б) Что показывает частное? Всегда ли можно выполнить деление?

в) Назвать действия первой и второй ступени.

Билет №4.

а) Как называются числа при делении?

б) Что показывает разноть двух чисел?

в) Вычислить: 15²

Билет №5.

а) Как из суммы вычесть число? Привести пример

б) Как называются числа при делении с остатком?

в) Вычислить: 4³

Билет №6.

а) Как сравнить четырехзначное и трехзначное числа? Два шестизначных числа?

б) Как вычесть сумму из числа?

в) Как найди делимое при делении с остатком? Пример.

2 конкурс.

Вывешивается объявление : «Цены повышены на 2%» и их ценники.

Старая цена

Новая цена

Ученикам необходимо на скорость посчитать новую цену.

3 конкурс.

1)    В карманах денег поровну. Из одного в другой карман положили 1 рубль. На сколько больше там стало?

2)    Подсчитай, какое стадо обслужить ребятам надо.

Индюшат, их 240, водит Катя на пригорок.

Машет прутиком Илья, напевая:

«8 уток, один я, куда утки, туда и я».

Что-то громко чересчур раскричались курицы,

Сотен пять их было, и они как развоюются!

А на речке уток 200, как закрякали все вместе.

3)    Сумма двух чисел больше одного из них на 17 и больше другого на 13. Чему равны эти числа?

4)    Назовите число, если половина – треть его.

5)    В саду 33 сучка, на каждом по 33 яблока. Сколько яблок всего?

6)    Из спичек составлено равенство. Оно неверное. Как переложить одну спичку, чтобы получилось верное равенство?

Игра № 14

Геометрическое поле чудес

Тема: Геометрические фигуры.

Цель: закрепить знания по теме

Содержание игры:

Учитель говорит, что сегодня все будут играть в геометрическое поле чудес.

Учитель повторяет с учениками:

·        Что такое геометрическая фигура;

·        Вспомнить изученные фигуры, найти их на плакате;

·        Дать определение фигур на плакате;

·        Какая наука изучает свойства геометрических фигур

Загаданные слова будут из учебников для старших классов и учитель показывает эти учебники..

Далее необходимо выбрать тройки игроков, выбор осуществляется после правильного ответа на вопрос по поднятой руке. Учитель показывает барабан и говорит, что обозначает каждый сектор.

х – открыть первую букву;

0 – назвать букву;

 - открыть последнюю букву;

∆ - переход хода;

ے – совет друга;

1. Выбор первой тройки.

а) Сосчитать, сколько углов, меньших 180⁰, изображено на рисунке.

Ответ : 10 углов

б) На рисунке изображены 4 угла. Величина одного из них известна. Найти градусные меры остальных трех углов.

          А                                                                             С

                                               O

                                                              30⁰

           В                                                                         D

в) Как убедиться, что площадь треугольника ACD больше площади треугольника DCE в 2 раза?

         B                                                                            C

        A                                                                             D

Задание.

Как называется фигура, которая получается от вращения прямоугольного треугольника вокруг катета (принадлежность клоуна).

2. Выбор второй тройки.

а) Сколько здесь треугольников?

Ответ: 18

б) Сколько прямоугольников?

Ответ: 18

в) Проведите два отрезка так, чтобы получилось 5 квадратов

Задание.

Как назвать четырехугольник, у которого две стороны параллельны, а две другие непараллельны? (Это слово часто употребляется в цирке)

3. Выбор третьей тройки.

а) Два прямоугольника имеют одну и ту же площадь. Длина первого прямоугольника равна 4 дм, а ширина 0,9 м. чему равна длина второго прямоугольника, если его ширина 3 дм.

б) Найдите объем прямоугольного параллелепипеда, если длина его равна 1,2 м, ширина 0,5 м, а высота 0,3м.

в) Из деревянного бруска, длина которого 8 см, ширина 0,6 дм и высота 4 см, вырезали куб с ребром 0,04 м. чему равен объем оставшейся части бруска?

Задание.

Как называется прямая, которая с окружностью имеет одну общую точку.

4. Игра со зрителями.

Вычислить площадь фигуры.

                      30 см

  15 см

                  35 см

                                 15 см

5. Финал

Как называется одна из сторон прямоугольного треугольника?

6. Супер-игра.

Как называли куб или шестигранник в Древней Греции?

Игра № 15

Запятая

Тема: Умножение десятичных дробей на 10, 100, 1000 и т.д.

Цель: научить умножать десятичную дробь на натуральное число 10, 100, 1000 и т.д.

Содержание игры:

Шесть учеников примерно одинакового роста надевают колпаки с написанными на них цифрами, а ученик поменьше одевает колпак с запятой. Учитель говорит ученику с запятой, что он может перебегать на различные места, в ряду учеников-цифр, но только в право и не очень быстро.

 Учитель  объясняет ученикам, что происходит с запятой при умножении на 10, когда ученик с запятой перебежал на одну цифру вправо. Когда же ученик перебегает на две цифры вправо, ученикам предлагается самим понять, на какое число была умножена десятичная дробь.

После этого учитель предлагает ученикам самим попробовать сформулировать правило умножения десятичной дроби на 10, 100, 1000 и т.д. Выслушав все предложения, учитель говорит четкое правило, и с помощью плаката еще раз показывает, как умножать десятичные дроби на 10, 100, 1000.

Дальше учитель вызывает других учеников и дает им другие колпаки.

Теперь ученик с колпаком перебегает право, а ученики говорят, на сколько была умножена десятичная дробь. А затем ученики говорят десятичную дробь, а ученик с запятой перебегает на необходимое место.

Игра № 16

Составь фигуру

Тема: Прямоугольный параллелепипед

Цель: познакомить детей с новой фигурой – прямоугольный параллелепипед, ввести понятие ребер, граней и вершин

Содержание игры:

На столе у каждого ученика развертка прямоугольного параллелепипеда, ученикам предлагается сложить фигуру. Главное – не рвать развертку, а последовательно складывать. Первым пяти участникам быстрее всех сложившим фигуру начисляется по баллу.

Далее учитель дает название новой фигуры: прямоугольный параллелепипед, говорит, что стороны прямоугольного параллелепипеда – это грани, а также показывает, что стороны граней называются ребрами прямоугольного параллелепипеда. Также учитель указывает на то, что в прямоугольном параллелепипеде три измерения: длина, ширина и высота.

Учитель просит посчитать количество граней, вершин и сторон прямоугольного параллелепипеда. Каждый ученик, кто быстрее всех и верно посчитает необходимое количество, получает по баллу.

Так как фигура у учеников перед глазами, то учитель предлагает им раскрасить противоположные грани одним цветом и сказать что-нибудь о противоположных гранях. За верный ответ начисляется по два балла.

После этого ученикам можно дать другую развертку и предложить им составить иную фигуру.

Затем ученики предлагается сравнить две полученные фигуры.

Теперь учитель может сказать название данной фигуры – куб, и что это прямоугольный параллелепипед, у которого все измерения одинаковы, и, смотря на полученную фигуру, ученики убеждаются в этом.

Последним же этапом изучения нового материала является работа с еще одной разверткой. Ученикам дается развертка куба, а на доске нарисованы три различных куба. необходимо узнать, какие из изображенных кубиков можно склеить из этой развертки.

В конце игры учитель подсчитывает количество баллов, набранных учащимися, и объявляет трех победителей.

Игра № 17

Письмо от сказочного героя

Тема: Проценты

Цель: познакомить учащихся с понятием проценты

Содержание игры:

Учитель говорит ученикам, что получил сегодня письмо от героини сказки «Золушка», в котором она хочет поделиться своими знаниями о процентах. Учитель зачитывает письмо.

7:2=

6,4:4=

1:4=

3:2=

4,3:4,3=

0,2·2-0,2²=

80:100=

После прочтения начала письма, учитель предлагает записать тему урока и дальше продолжает читать письмо и параллельно объяснять тему урока от лица Золушки. Объяснение материала можно проводить методом беседы с учениками.

В конце урока ученикам, которые активно работали на уроке, учитель от имени Золушки может подарить нарисованную хрустальную туфельку девочкам, а мальчикам нарисованную шпагу.

Игра № 18

Дерево

Тема: Умножения десятичных дробей на натуральное число

Цель: закрепить правило умножения десятичных дробей на натуральное число

Содержание игры:

Перед учениками плакат с изображением дерева и висящих на нем плодов, в которых написаны буква и число. Рядом с плакатом на доске выписаны примеры, соответствующие данной теме. Ученикам необходимо вписать в кружки буквы соответствующие найденным ответам на дереве. Ученики по-очереди выходят, поговаривают правило умножения десятичной дроби на натуральное число и вписывают правильные ответы, остальные ученики следят за правильным выполнением того или иного примера. Если ученик решил неправильно, то они поправляют его или сами выходят к доске. Затем читают получившееся слово.

Учитель может пояснить значение получившегося слова или попросить учеников найти его в словаре.

В данной игре учитель поясняет значение получившегося слова.

«Полученное слово «КИГАЛИЯ» является названием дерева, которое растет в Африке и называется «колбасным» деревом. Его зрелые плоды похожи на вареные колбаски длиной до 60 см. этими колбасками охотно питаются животные, но для человека они не съедобны. Их используют для производства некоторых лекарств и красок».

3,6·3=   

0,25·4=

0,05·4=

0,004·6=

2,6·5=

0,125·8=

0,02·15=

Игра № 19

Бабочка

Тема: Деление десятичных дробей на натуральное число

Цель: закрепить правило деления десятичных дробей на натуральное число

Содержание игры:

Перед учениками плакат с изображением дерева , а вокруг дерева бабочки, в которые вписаны буква и число. Рядом с плакатом на доске выписаны примеры, соответствующие данной теме. Ученикам необходимо вписать в кружки ответы, и по ответу найти бабочку и посадить её на дерево. Учитель может сделать небольшое предисловие к игре:

«Некоторые бабочки, как и птицы, улетают на зимовку. Узнайте название бабочки, которая из Северной Америки летит в Южную, преодолевая расстояние более трех тысяч километров».

3,6·3=   

0,25·4=

0,05·4=

0,004·6=

2,6·5=

0,125·8=

0,02·15=

Полученное слова МОНАРХ. Сотни тысяч этих бабочек, разместившись на ветках деревьев, создают впечатление пестрой листвы и цветов.

Игра № 20

Встреча со знаменитым ученым.

Тема: Микрокалькулятор

Цель: закрепить знания учащихся по теме

Содержание игры:

На уроке учитель предстает перед учениками в виде немецкого физика, изобретателя и математика Готфрильда Вильгельма Лейбница, который изобрел первый калькулятор – арифмометр. Он рассказывает о своем изобретении, что калькулятор был создан им в 1673 году и выполнял все четыре арифметических действия. Идея создания машины, выполняющей вычисления, появилась у него после его знакомства с голландским математиком и астрономом Христианом Гюйгенсом. Огромное количество вычислений, которое приходилось делать астроному, навело его на мысль о создании механического устройства, которое могло бы облегчить такие расчёты.

Далее учитель показывает свой калькулятор.

Также он говорит, что слышал, что современные люди пользуются новыми видами калькуляторов и просит их показать. Ученики показывают свой калькулятор.

Далее учитель просит рассказать учеников о функциях такого нового калькулятора и показать его в применении решения различных примерах.

Учитель спрашивает:

1)    Какие арифметические действия можно выполнять с помощью микрокалькулятора?

2)    С чего начинается работа на микрокалькуляторе?

3)    Как ввести в микрокалькулятор натуральное число? Десятичную дробь?

4)    Как сбросить число с индикатора?

5)    Как сложить на микрокалькуляторе два числа?

6)    Как вычесть на микрокалькуляторе два числа?

7)    Как умножить на микрокалькуляторе два числа?

8)    Как поделить на микрокалькуляторе два числа?

9)    А кто вспомнит, от какого слова произошло слово микрокалькулятор?

Далее можно предложить решить любые примеры на микрокалькуляторе.

Учеников, которые много отвечали, Лейбниц поощряет оценкой  и званием ученого в области микрокалькулятора.

Скачано с www.znanio.ru