Сборник нестандартных задач, направленных на развитие логического мышления младших школьников

 

 

 

 

 

 

 

Сборник нестандартных задач, направленных на развитие логического мышления младших школьников

 

            Сборник нестандартных задач, призванный внести яркие краски в мир логики младших школьников. Обучение должно быть не только познавательным, но и увлекательным, а развитие логического мышления - залогом успешного будущего.

         В этом сборнике вы найдете задачи, которые нестандартны по форме и содержанию. Они не требуют заучивания формул или правил, а направлены на развитие логического мышления, способности анализировать, находить закономерности, делать выводы и приходить к решению нестандартным путём.

         Мы надеемся, что этот сборник поможет вам сделать уроки увлекательными и эффективными, а также повысить интерес обучения к математике, развить у детей логические навыки, повысить уровень логического мышления.

 

1.       Логические задачи.

1.1.          Задачи на переливание.

      1. Имеются двухлитровая и пятилитровая банки. Как сделать так, чтобы, в одной из них оказался ровно один литр воды?

      2. Для марш-броска солдату необходимо иметь 4 литра воды. Больше он взять не может. На базе, где имеется источник воды, есть только 5-литровые фляги и 3-литровые банки. Как с помощью одной фляги и одной банки набрать 4 литра во флягу?
      3. Как, имея 5-литровое ведро и 9-литровую банку, набрать из реки ровно три литра воды?

      4. Из полного восьмилитрового ведра отлейте 4 л с помощью пустых 3-литровой банки и 5-литрового бидона. (Пользоваться другими емкостями и выливать воду на землю нельзя).

      5. Отлейте из цистерны 13 л молока, пользуясь бидонами емкостью 17 л и 5 л.

      6. Винни Пуху нужно покрасить забор. Он имеет 12 л краски и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 л. У него 2 сосуда: один – вместимостью в 8 л, а другой – вместимостью в 5 л. Каким образом налить 6 л краски в сосуд на 8 л? Какое наименьшее число переливаний необходимо при этом сделать?

      7. Имеются два полных десятилитровых бидона молока и пустые кастрюли емкостью четыре литра и пять литров. Отлейте по 2 л молока в каждую кастрюлю.

 

1.2.          Задачи на взвешивание.

    1. Из 27 монет одна фальшивая - она легче остальных. За какое наименьшее число взвешиваний на чашечных весах без гирь можно определить фальшивую монету?

    2. На весах, которые находятся в равновесии, на одной чаше лежат 3 груши и гиря массой 20 г. На другой чаше – банан и две гири по 20 г. Какова масса одного банана, если масса одной груши 60 г.?

    3. Золотоискатель Джек добыл 9 кг песка. Сможет ли он за три взвешивания отмерить 2 кг песка с помощью двухчашечных весов с двумя гирями – 200 г и 50 г?

    4. На одной чашке весов лежат 6 одинаковых яблок и 3 одинаковые груши, на другой чашке – 3 таких же яблоке и 5 таких же груш. Весы находятся в равновесии. Что легче: яблоко или груша?

    5. Геологи нашли 7 камней, массы которых 1 кг, 2 кг, 3 кг, 4 кг, 5 кг, 6 кг, 7 кг. Они разложили их в рюкзаки так, что в каждом из рюкзаков масса камней была одинакова. Как это сделали?

    6. У хозяйки есть рычажные весы и гиря в 100г. Как за три взвешивания она может отвесить 700 г. крупы?

    7. Дыня весит столько же, сколько 5 яблок, а одно яблоко - как 2 огурца. Сколько понадобится огурцов, чтобы уравновесить одну дыню? А сколько огурцов понадобится, чтобы уравновесить дыню и яблоко?

 

1.3.          Задачи на переправы.

    1. Крестьянин с волком, козой и мешком капусты подошел к реке. Ему надо переправиться на другой берег, однако в лодке вместе с ним может поместиться либо волк, либо коза, либо капуста. Оставшись на берегу без крестьянина, волк съест козу, а коза – капусту. Как крестьянину переправиться без потерь?

    2. К левому берегу реки подошла мама с пятью сыновьями 6, 7, 8, 9 и 10 лет. Есть трехместная лодка. Грести может только мама. Если на берегу без неё останутся дети с разницей в возрасте 1 год, они подерутся. Как маме переправить всех на правый берег так, чтобы никто не подрался?

    3. Два человека одновременно подошли к реке. У берега была одноместная лодка. На ней оба сумели переправиться на противоположный берег. Как такое могло быть?

    4. Трое туристов должны перебраться с одного берега реки на другой. В их распоряжении старая лодка, которая может выдержать нагрузку всего в 100 кг. Вес одного из туристов 45 кг, второго — 50 кг, третьего — 80 кг. Как должны они действовать, чтобы перебраться на другой берег?

    5. Семья (папа, мама, сын и бабушка) ночью подошла к мосту, способному выдержать только двух человек одновременно. По мосту можно двигаться только с фонариком. Известно, что папа может перейти мост в одну сторону за минуту, мама – за две, сын – за пять и бабушка – за десять минут. Если по мосту движутся двое, время перехода определяется более медленным из двоих. Как семье переправиться менее чем за 18 минут?

    6. К берегу подходит мальчик Леня с кошкой, собакой и петухом. Эти трое терпеть не могут друг друга, хотя уважают и слушаются Леню. Поэтому никаких двух их них нельзя оставить на берегу одних. Леня нашел у берега лодку, в которую, кроме него, поместится 2 животных. Как переправиться?

    7. После долгого путешествия на левом берегу реки остановились пять гномов, которые тащат с собой большой мешок с золотом. В их распоряжении имеется одна лодка грузоподъёмностью 70 кг, которая проплывает от одного берега до другого за 6 минут (вне зависимости от нагрузки). Известно, что каждый из гномов весит 20 кг, а мешок с золотом – 50 кг. Золото нельзя оставлять на берегу без присмотра, кто-то из гномов должен всегда быть рядом с мешком. Помогите гномам переправиться через реку за 30 минут.

 

1.4.          Задачи на разъезды.

    1. Пробка в переулке. В узком переулке, заставленном машинами, 3 синих машины хотят проехать направо, 3 белых - налево. Сбоку есть только одно свободное место.

Как им разъехаться?

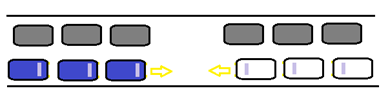
    2. На одноколейной железной дороге встретились два поезда по 5 вагонов каждый. Поблизости есть небольшое тупиковое ответвление, но в него помещается только тепловоз с двумя вагонами или 3 вагона. Как поездам разъехаться?

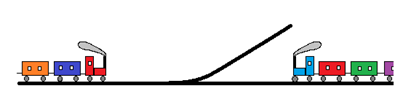
    3. Поезд Б приближается к станции железной дороги, но его нагоняет быстрее идущий поезд А, который необходимо пропустить вперёд. У станции от главного пути отходит боковая ветка, куда можно отвести на время вагоны с главного пути, но ветка эта настолько короткая, что на ней не помещается весь поезд Б. Спрашивается, как всё-таки пропустить поезд А вперёд?

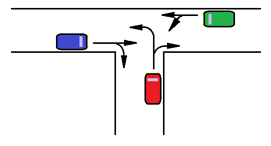
    4. На Т-образный перекресток со всех сторон приезжает примерно поровну машин, и машины с каждого направления делятся примерно поровну, выбирая одно из двух направлений дальнейшего движения. Как составить расписание работы светофора на этом перекрестке?

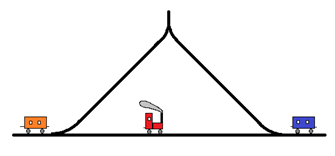
    5. Два вагона стоят с двух сторон от железнодорожного путевого треугольника. Между ними – маневровый паровоз. Как ему действовать, чтобы поменять вагоны местами? В тупик на конце треугольника (на рисунке – вверху) помещается только один вагон или один паровоз. Маневровый паровоз может прицепляться к вагону любой стороной, и ехать может в любую сторону – хоть тянуть, хоть толкать. В конце он должен оказаться на том же месте, на котором был вначале.

 

1.5.          Задачи на дележи

    1. Как разделить 7 яблок между 12 мальчиками, если ни одно яблоко нельзя разрезать более, чем на пять частей?

    2. Для изготовления поделки на уроке труда разрезали шнурок в 7 местах. Сколько частей шнурка получилось?

    3. Три купца должны поделить между собой 21 бочонок, из которых 7 бочонков полных кваса, 7 полных наполовину и 7 пустых. Спрашивается, как они могут поделиться так, чтобы каждый имел одинаковое количество кваса и одинаковое количество бочонков, причём переливать квас из бочонка в бочонок нельзя.

    4. У Максима и Никиты вместе 240 фишек. Максим подарил Никите 40 фишек. У них стало фишек поровну. Сколько фишек было у каждого мальчика до этого?

    5. 3 курицы - несушки за 3 дня снесли 3 яйца. Сколько яиц снесут 6 кур за 9 дней при тех же условиях?

    6. Старик, имевший трех сыновей, распорядился, чтобы oни после его смерти поделили принадлежащее ему стадо лошадей так, чтобы старший взял половину всех лошадей, средний - треть и младший - девятую часть всех лошадей. Старик умер и оставил 17 лошадей. Сыновья начали делить, но оказалось, что число 17 не делится ни на 2, ни на 3, ни на 9. В недоумении, как им быть, братья обратились к мудрецу. Тот приехал к ним на собственной лошади и разделил все по завещанию. Как он сделал?

 

1.6.          Задачи на соответствие и порядок.

    1. Жили три друга: учитель, врач и рабочий. Их фамилии Борисов, Иванов и Семенов. У учителя нет ни братьев, ни сестер, он самый младший из друзей. Семенов старше врача и женат на сестре Борисова. Назовите фамилии учителя, врача и рабочего.

    2. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. В какой сосуд налита каждая из жидкостей?

    3. В очереди за билетами в кино стоят Юра, Миша, Володя, Саша и Олег. Известно, что: Юра купит билет раньше, чем Миша, но позже Олега; Володя и Олег не стоят рядом; Саша не находится рядом ни с Олегом, ни с Юрой, ни с Володей. Кто за кем стоит?

    4. Три подруги вышли в белом, зеленом и синем платьях и в туфлях таких же цветов. Известно, что только у Ани цвет платья и цвет туфель совпадают. Ни туфли, ни платье Вали не были белыми. Наташа была в зеленых туфлях. Определите цвет платья и туфель на каждой из подруг.

    5. Меня зовут Иваном Сергеевичем, моего деда – Петром Николаевичем. Назвать имя и отчество моего отца.

    6. Встретились Андрей, Боря, Ваня и Гриша. Боря не самый высокий, но выше Андрея и Гриши, а Андрей не выше Гриши. Построй ребят по росту.

    7. Отца одного мужчины зовут Николай Петрович, а сына этого мужчины – Алексей Владимирович. Каковы имя и отчество этого мужчины?

 

1.7.          Истинностные задачи.

    1. На необитаемом острове растут три дерева - дуб, береза и сосна. Под одним из них пираты зарыли клад, а на деревья повесили таблички. На дуб: клад зарыт под сосной; на березу: клад зарыт не здесь; на сосну: клад зарыт под березой. Узнайте, под каким деревом зарыт пиратский клад, если из трех надписей две истинные, а одна ложная.

    2. Украли у Ивана Царевича Василису Прекрасную. Поехал он выручать ее. Поймал Змея Горыныча, Бабу Ягу, Кощея Бессмертного и Лешего - Иван Царевич знал, что один из них украл ее. И спрашивает: «Кто украл Василису?» Змей Горыныч, Баба Яга и Кощей Бессмертный ответили: «Не я», а Леший - «Не знаю». Потом оказалось, что двое из них сказали правду, а двое - неправду. Знает ли Леший, кто украл Василису?

    3. Перед Полиной стоят три знакомых друг с другом человека. Один из них рыцарь (говорит всегда правду), другой лжец (всегда лжет), а третий плут (может сказать правду, а может ложь). Человек, стоящий слева сказал, что рядом с ним стоит рыцарь. Человек, стоящий в центре, назвал себя плутом. А человек справа сказал, что рядом с ним стоит лжец. Кто же стоит слева, кто справа, кто в центре?

    4. В гонках участвуют 5 яхт. Капитан Врунгель сказал, что яхта "Беда" лидирует - идёт на первом месте. Лом сказал, что "Беда" в первой тройке, а Фукс сказал, что "Беда" не первая и не вторая. Двое из них ошибаются. На каком месте сейчас яхта "Беда№, если у "Беды" на самом деле нечётное место.

    5. Собрались 4 котёнка. Первый сказал:" Я не лжец!" Второй подтвердил:" Ты не лжец" Третий обобщил:" Да вы оба не лжецы!" И четвёртый заключил: «Мы все не лжецы!" Хотя бы кто-то из них врёт, но не все. Сколько из них лжецов?

    6. Петр, Андрей и Ерофей рассматривают календарь. «Сегодня понедельник», — сказал Петр. «Завтра вторник», — сказал Андрей. «А вчера была суббота», — сказал Ерофей. Могут ли все трое быть правы?

    7. Сегодня у Паши день рождения. Его друг Коля говорит, что Паше больше 11 лет, а его друг Толя — что Паше больше 10 лет. Сколько лет исполнилось Паше, если известно, что ровно один из его друзей ошибся?

 

1.8.          Задачи на распиливание, разрезание.

1. На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, то получится - 5 кусков, если по жёлтым – 7 кусков, а если по зелёным – 11 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?

2. Взяли несколько досок и распилили их. Всего сделали 11 поперечных распилов, в итоге получилось 16 кусков. Сколько досок взяли?

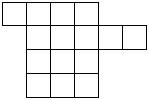
3. Попробуйте разрезать изображенную на рисунке фигуру на 3 равные по форме части:

4. Вова распилил бревно на 6 частей. Сколько для этого он сделал распилов?

5. Имеются бревна длиной 4 м и 5 м одинаковой толщины. Бревно перепиливается за 1 минуту. Надо напилить 20 бревен длиной 1 м. можно пилить только 4-метровые или только 5-метровые бревна. Какие бревна надо пилить? Почему?

6. Разрежьте данную фигуру на 5 равных по форме частей:

7. Разрежьте эту фигуру на 5 фигур из четырех клеток разной формы таким образом, чтобы в каждой их них была закрашена только одна черная клетка.

 

1.9.          Задачи на принцип Дирихле. (Данные виды заданий идут для обучающихся 6-7 классов и старше).

    1. В первенстве по футболу участвует 18 команд. Первенство разыгрывается в один круг, любые две команды встречаются только один раз. Известно, что каждая команда сыграла какое-то число игр. Докажите, что найдутся две команды, сыгравшие одинаковое число игр.

    2. В городе живет 200 тыс. жителей. Докажите, что в городе найдутся хотя бы 2 человека с одинаковым числом волос на голове. Считайте, что у человека на голове не больше 150 тыс. волос.

 

1.10.      Задачи на поиск инвариантного свойства. (Данные виды заданий идут для обучающихся 6-7 классов).

    1. На шахматной доске стоит черный слон и белая ладья. Белые, как водится, ходят первыми. Доказать, что при правильной игре черные никогда не выиграют.

    2. Мише учитель математики поставил в дневник отметку «2». Миша, желая скрыть от мамы данный факт, порвал свой дневник на 4 части. Этого ему показалось мало, поэтому некоторые из этих частей (может быть и не все) он порвал на 4 части и так далее. Мама нашла 20 «кусочков» дневника. Все ли куски нашла мама?

 

2.       Геометрические задачи.

1.      На одной плоскости размещены 11 шестерёнок, которые соединены по цепочке. Как вы думаете, смогут ли все шестерёнки вращаться одновременно?

2.     Как вы думаете, сколько квадратов изображено на рисунке?

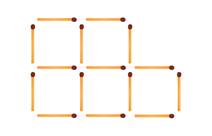
3.     Уберите три спички так, чтобы осталось три квадрата.

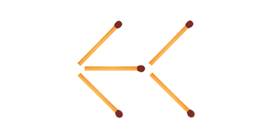
4.     Переложите три спички так, чтобы стрелка показывала в противоположном направлении.

5.     Переложите одну спичку, чтобы равенство стало верным.

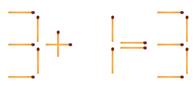
6.     Графический диктант. Отступить 1 клетку вниз. 3 право; 1 верх; 1 право; 8 низ; 1 право; 1низ; 4 право; 8 низ; 1 лево; 5 верх; 1 лево; 5 низ; 1 лево; 5 верх; 2 лево; 5 низ; 1 лево; 5 верх; 1 лево; 5 низ; 1 лево; 8 верх; 1 право; 6 верх; 2 лево; 2 верх.

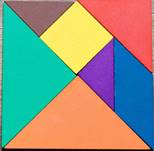
7.     Собери танграм.

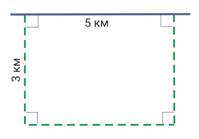
8.     На дороге произошла авария, поэтому водителям приходится объезжать этот участок по другому пути. Он отмечен на картинке пунктирной линией. На сколько этот новый путь длиннее обычной дороги?

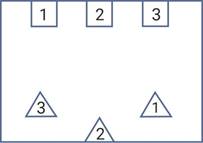
9.     Перед вами шесть фигур. Ваша задача ─ соединить их попарно непроизвольными и непрерывными линиями так, чтобы они не пересекались.

10. К вам в гости пришли 8 гостей и вы хотите их напоить чаем с вкуснейшим тортом! Как поделить плоский круглый торт на 8 равных частей за три прямолинейных надреза ножа? При это перекладывать куски нельзя!

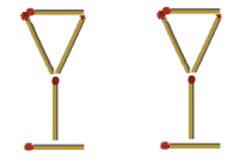
11. На рисунке из 10 спичек выложено 2 бокала. Переложите 6 спичек так, чтобы получился домик.

12. Решётка из спичек образует 9 одинаковых квадратов. Уберите 4 спички так, чтобы осталось ровно 5 квадратов.

 

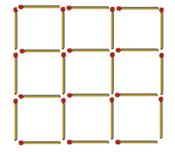
3.       Нестандартные арифметические задачи.

1.     Сколько существует трехзначных чисел, все цифры которых – 1, 2 или 3?

2.     Петя нашел один гриб, Коля – два, а Паша – три. Мама дала им 18 орехов и велела разделить их по заслугам. Сколько орехов получил каждый?

3.     В гараже стоят 750 автомобилей. Грузовые автомобили имеют по 6 колес, а легковые по 4 колеса. Сколько каких автомобилей в гараже, если колес всего 3024?

4.     Путь, который прошли туристы за понедельник, изображается на карте отрезком в 3 см, а путь, пройденный во вторник, – отрезком в 15 мм. В какой день они прошли больше и во сколько раз?

5.     Постоялец гостиницы, не имея денег, договорился с хозяином, что будет расплачиваться, отдавая ему каждый день одно из семи звеньев своей золотой цепочки. И они, поразмыслив, смогли устроить так, что у хозяина каждый день прибавлялось по одному звену цепи. Как они это сделали?

6.     1 февраля 1996 г. был четверг. Каким днем недели было 1 марта 1996 г.?

7.     Коля считает, что если сумма первых трех цифр номера автобусного билета равна сумме последних трех цифр, то билет – счастливый. Билет с номером 198675 – счастливый. Какие два ближайших к нему билета тоже счастливые?

8.     Попытайся понять, как составлена эта последовательность: 720, 360, 120, 30. Напиши еще два ее члена.

9.     Илья стоит в хороводе. Пятый слева от Ильи тот же, что и шестой справа. Сколько людей в хороводе?

10. Три брата пришли на постоялый двор, заказали пельмени и улеглись спать. Когда старший брат проснулся, он увидел на столе пельмени, пересчитал их и съел свою долю. После этого он снова уснул. Проснулся средний брат, пересчитал пельмени на столе и съел одну треть, не зная, что старший брат уже поел. После этого средний брат тоже уснул. Наконец, проснулся младший брат. Он съел третью часть имевшихся на столе пельменей. После этого он разбудил старшего и среднего брата и предложил им съесть оставшиеся 24 пельменя. Как должны братья разделить эти пельмени между собой?

11. Какое число в задаче на вычисление пропущено: 51: ... – 12?

12. Змей Горыныч вызвал на бой трех богатырей. Сколько голов должен отсечь каждый богатырь, если у змея их 12, а богатыри поделили его головы поровну?

 

4.       Комбинаторные задачи.

1.     4 парусника готовились к соревнованиям. У каждого спортсмена был свой белый корабль. Судьи решили, что надо раскрасить паруса, чтобы парусники были видны издалека, и было ясно, кто из спортсменов идет впереди, кто запаздывает. Покажите, кА по-разному раскрасили паруса, если были всего 2 краски.

2.     Помоги расставить 5 чашек на 3 полки разными способами так, чтобы на каждой полке стояли чашки.

3.     Запиши значения выражений 2+1, 3-1, 3-2. Какие цифры использованы для записи чисел? Запиши все возможные перестановки этих цифр, без повторов. Подчеркни ту запись, которая обозначает отрезок чисел, стоящих по порядку, в обратном порядке.

4.     Три поросенка Ниф-Ниф, Нуф-Нуф и Наф-Наф решили построить себе домики. Выбрали три прекрасных места: у реки, на озере и на горе. Найди все возможные варианты их размещения с помощью таблицы.

5.     У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?

6.     Какие трехзначные числа можно составить из цифр 0, 2, 4?

7.     Как можно рассадить на скамейке Аню (А), Мишу (М), Колю (К) и Риту (Р), чтобы девочки с мальчиками не чередовались? Построй дерево возможных вариантов. Какие варианты у тебя получились?

8.     При встрече каждый из друзей пожал другому руку. Сколько всего было рукопожатий, если встретились 7 друзей?

9.     На прием в больницу отправились Алексей, Даша, Маша, Саша, Карина, Катя, Лилия. Сколькими разными способами они могут встать в очередь у медицинского кабинета?

10. Сколько различных трёхзначных чисел можно составить при помощи цифр 4, 7, 9, так чтобы цифры в записи не повторялись?

11. В пятницу в пятом классе 5 уроков: музыка, математика, русский язык, литература и английский. Сколько различных способов составления расписания на пятницу существует?

12. Одна обезьяна съела 8 бананов, вторая - 24, третья 16, а четвертая - 9. Сколько бананов съели две обезьяны?

5.   Простейшие задачи, имеющие вероятностное содержание. (Данный вид заданий решается в среднем звене)

5.1. Определение вида события.

1. Бросают кубик. Какое из событий достоверное:

1) выпадение числа не больше, чем 5;

2) выпадение чётного числа;

3) выпадение числа меньше, чем 7;

4) выпадение числа больше, чем 4?

2. В коробке лежат шарики: 4 белых, 5 красных и 3 чёрных. Наугад вынимается один шарик. Какое событие наиболее вероятно:

1) вынутый шарик не белый;

2) вынутый шарик красный;

3) вынутый шарик не чёрный;

4) вынутый шарик белый?

5.2. Подсчет количества возможных исходов и исходов благоприятных для данного события.

1. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?

2. Петя, Вика, Катя, Игорь, Антон, Полина бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.

5.3.    Выявление более вероятных и менее вероятных событий.

1. В коробке лежат черные и белые шары. Из нее наугад вытягивают один шар. Используя выражение «более вероятное», «менее вероятное», «равновероятные события», сравните возможность наступления случайных событий А и В, где:

А: вытянутый шар будет белым;

В: вытянутый шар будет черным.

2. На экзамене 25 билетов. Сергей выучил 20 из них. Найдите вероятность того, что Сергею попадется выученный билет.

5.4. Нахождение вероятности событий с использованием классического определения вероятности.

1. Монету бросают дважды. Найдите вероятность того, что «орёл» выпадет один или два раза.

2. Аня, Боря, Витя, Гуля и Дима пошли в поход. Им нужно назначить двух дежурных. Они написали свои имена на одинаковых бумажках, сложили их в пустой рюкзак и вынули наугад две бумажки. Какова вероятность того, что дежурить будут два мальчика? Две девочки? Мальчик и девочка?