
2.
|
A |
B |
A^B |
A v B |
¬A |
¬B |
A→B |
A≡B |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
В питоне |
and |
or |
not(A) |
not(B) |
<= |
== |
|
2. 1) (x ∨ y) → (z ≡ x)
|
Переменная 1 |
Переменная 2 |
Переменная 3 |
Функция |
|
??? |
??? |
??? |
F |
|
0 |
0 |
0 |
|
|
0 |
0 |
Решение
При F=0, после if надо писать not
print("x y z")
for x in range(0, 2):
for y in range(0, 2):
for z in range(0, 2):
if not((x or y) <= (z == x)):
print(x, y, z)
Вывод Питон
x y z
0 1 1
1 0 0
1 1 0
Сопоставляем и находим ответ xzy
2. 2) ((x → y) ≡ (y → z)) ∧ (y ∨ w)
|
Перем 1 |
Перем 2 |
Перем 3 |
Перем 4 |
Функция |
|
??? |
??? |
??? |
??? |
F |
|
0 |
0 |
1 |
||
|
0 |
0 |
0 |
1 |
|
|
0 |
1 |
Решение
При F=1, после if not писать не нужно
print("x y z w")
for x in range(0, 2):
for y in range(0, 2):
for z in range(0, 2):
for w in range(0, 2):
if ((x <= y) == (y <= z)) and (y or w):
print(x, y, z, w)
Вывод Питон
x y z w
0 0 0 1
0 0 1 1
0 1 1 0
0 1 1 1
1 1 1 0
1 1 1 1
Сопоставляем и находим ответ xzwy
6. 1) Повтори 4 [Вперёд 8 Направо 90]
Повтори 3 [Вперёд 12 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом: Повтори 4 [Вперёд 8 Направо 90]
и находиться вне области, ограниченной линией, заданной данным алгоритмом: Повтори 3 [Вперёд 12 Направо 120]. Точки на линии учитывать не следует.
Решение
 В
кумире набираем код, не забываем масштаб 1 к 1 использовать Черепаха
В
кумире набираем код, не забываем масштаб 1 к 1 использовать Черепаха
алг
нач
. опустить хвост
. нц 4 раз
. . вперед(8)
. . вправо(90)
. кц
. нц 3 раз
. . вперед(12)
. . вправо(120)
. кц
кон
Скрин скидываем в Paint и там считаем точки внутри квадрата, но вне треугольника.
Ответ 13
6. 2) Повтори 5 [Вперёд 9 Направо 90 Вперёд 3 Направо 90]
Определите количество точек с целочисленными координатами, лежащих внутри или на границе области, которую ограничивает заданная алгоритмом линия.
 Решение
Решение
В данном задании считаем кол-во точек и НА ЛИНИИ использовать Черепаха
алг
нач
. опустить хвост
. нц 5 раз
. . вперед(9)
. . вправо(90)
. . вперед(3)
. . вправо(90)
. кц
кон
Скрин скидываем в Paint и там считаем точки на прямоугольнике (в том числе и на линии)
Ответ 40
6. 3) Исполнитель Кузнечик перемещается на координатной
плоскости и может выполнять две команды: Вперед(х) и Вправо. По
команде Вперед(х) Кузнечик перемещается вперед на расстояние х, по
команде Вправо – поворачивается вправо на 90 градусов.
Повтори 13 раз [
Вперед(10)
Вправо
Вперед(4)
Повтори 3 раз [Вправо Вперед (3)]
]
Необходимо написать такой алгоритм, который содержит минимальное количество команд Вперед(х) и не содержит циклов, после выполнения которого исполнитель приходит в ту же точку, что и после выполнения алгоритма из задания. В качестве ответа запишите сумму значений х в командах Вперед(х) в полученном алгоритме.
Решение.
Прописываем код в Кумире и видим, какая фигура у нас получается (для начала без масштаба 1 к 1, чтобы видеть всю фигуру целиком). Кузнечика заменим на Черепаху
![]() использовать Черепаха
использовать Черепаха
алг
нач
. опустить хвост
. нц 13 раз
. . вперед(10)
. . вправо(90)
. . вперед(4)
. . нц 3 раз
. . . вправо(90)
. . . вперед(3)
. . кц
![]() . кц
. кц
кон
Видно, что фигура повторяется 13 раз
Увеличиваем масштаб 1к1 и вычисляем высоту одной из фигур.

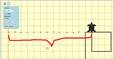
Высота вышла 10 клеток. Умножаем на 13 (кол-во фигур) и находим общую высоту всей фигуры: 10*13=130 точек.
Далее определяем, на сколько нужно передвинутся черепахе направо, чтобы дойти до точки: 13
В итоге, просуммировав получим ответ 130+13=143 точки
Ответ 143
6. 4) Направо 198
Повтори 5 [Вперёд 10 Налево 144]
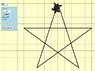
Определите, сколько различных треугольников содержит фигура, нарисованная Черепахой.
 Решение
Решение
использовать Черепаха
алг
нач
. опустить хвост
. вправо (198)
. нц 5 раз
. . вперед(10)
. . влево(144)
. кц
кон
При подсчете кол-ва фигур, масштаб не имеет значения. Подсчитаем треугольники, их получится 10
Ответ 10
6. 5) Повтори 13 [ Направо 135 Вперед 5 ]
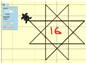
Найдите количество точек фигуры, образованных пересечением отрезков, без учета концов самих отрезков.
 Решение
Решение
использовать Черепаха
алг
нач
. опустить хвост
. нц 13 раз
. . вправо(135)
. . вперед(5)
. кц
кон
Масштаб в этом номере не обязателен. Подсчитаем кол-во пересекающихся точек. Их получилось 16
Ответ 16
6. 6) Повтори 5 [
Повтори 2 [ Вперед 3 Налево 45 Вперед 3 Направо 90 ]
Направо 180 ]
Найдите минимальную длину линии, которой можно нарисовать эту фигуру.
Решение
использовать Черепаха
 алг
алг
нач
. опустить хвост
. нц 5 раз
. . нц 2 раз
. . . вперед(3)
. . . влево(45)
. . . вперед(3)
. . . вправо(90)
. . кц
. . вправо(180)
. кц
кон
По сути, это нахождение периметра. Определяем, что длина одной линии 3. А таких линий 16, в итоге 3*16=48.
Ответ 48
6. 7) Повтори 5 [ Повтори 3 [ Вперед 2 Направо 270] Вперед 4]
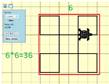
Найдите минимальную площадь выпуклого многоугольника, включающего фигуру.
 Решение
Решение
использовать Черепаха
алг
нач
. опустить хвост
. нц 5 раз
. . нц 3 раз
. . . вперед(2)
. . . вправо(270)
. . кц
. . вперед(4)
. кц
кон
В выпуклый многоугольник должна полностью входить фигура, нарисованная Черепахой. В данном случае, это квадрат со стороной 6. В итоге площадь 6*6=36
Ответ 36
6. 8) Повтори k [
Повтори 4 [ Вперед 30 Направо 90 ] Поднять хвост
Вперед 5 Направо 90 Вперед 5 Опустить хвост
Направо 270 ]
При каком значении параметра k нарисованная на поле траектория Черепахи пройдет несколько раз ровно через 20 точек?
Решение
В начале напишем код, записав вместо к единицу, чтобы посмотреть, какая фигура получается.
 использовать
Черепаха
использовать
Черепаха
алг
нач
. нц 1 раз
.опустить хвост
. . нц 4 раз
. . . вперед(30)
. . . вправо(90)
. . кц
. . поднять хвост
. . вперед(5)
. . вправо(90)
. . вперед(5)
. . вправо(270)
. кц
кон
Получается квадрат и при этом Черепаха перемещается в другую точку. Будем менять значение к до тех пор, пока пересечений не будет ровно 20 штук. Их будет 20 при к=5.
использовать Черепаха
алг
 нач
нач
. нц 5 раз
. . опустить хвост
. . нц 4 раз
. . . вперед(30)
. . . вправо(90)
. . кц
. . поднять хвост
. . вперед(5)
. . вправо(90)
. . вперед(5)
. . вправо(270)
. кц
кон
![]() 6. 9) В
начальный момент Черепаха находится в начале координат, её голова
направлена вдоль положительного направления оси абсцисс, хвост опущен.
6. 9) В
начальный момент Черепаха находится в начале координат, её голова
направлена вдоль положительного направления оси абсцисс, хвост опущен.
Повтори 40 [Налево 45 Вперёд 400 Направо 90]
Определите, сколько точек с целыми положительными координатами (x, y) будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
Решение
Не забываем, что в данной задаче голова Черепахи повернута по оси х, поэтому, в начале, поворачиваем направо 90.
 использовать Черепаха
использовать Черепаха
алг
нач
. вправо(90)
. опустить хвост
. нц 40 раз
. . влево(45)
. . вперед(400)
. . вправо(90)
. кц
 кон
кон
Рисунок очень большой, в масштабе подсчитать не реально. Поэтому определим площадь трапеции в той зоне, где х и у положительны.
По теореме Пифагора определяем один из катетов выделенного треугольника. Получается число больше 282, но меньше 283. Это означает, что 282 точки влезает в фигуру, а 283-ая нет. Следовательно, нижнее основание трапеции 282+400+282 точки. Верхняя 400 точек, а высота 282 точки. Находим площадь трапеции s=(400+282+400+282)/2 * 282 = 192324
Ответ 192324
6. 9) Чертёжнику был дан для исполнения следующий
алгоритм:
сместиться на (0, 12)
сместиться на (5, -12)
сместиться на (-10, 0)
сместиться на (5, 12)
сместиться на (0, 4)
сместиться на (3, -4)
сместиться на (-6, 0)
сместиться на (3, 4)
Найдите разность между максимальным и минимальным периметром нарисованных треугольников.
Решение
Чертежник тоже можно делать в Кумире
 использовать Чертежник
использовать Чертежник
алг
нач
. опустить перо
. сместиться на вектор (0,12)
. сместиться на вектор (5,-12)
. сместиться на вектор (-10,0)
. сместиться на вектор (5,12)
. сместиться на вектор (0,4)
. сместиться на вектор (3,-4)
. сместиться на вектор (-6,0)
. сместиться на вектор (3,4)
кон
Минимальный треугольник это abc. a=3, b=4 и т.к. он египетский, то с=5. Периметр будет Р1=3+4+5=12.
Максимальный треугольник это eeff. d=12, f=5. По теореме Пифагора находим e=13. Периметр его будет Р2=13+13+5+5=36
Разница 36-12=24
Ответ 24
6. 10) Повтори 2 [Вперёд 7 Направо 90 Вперёд 8 Направо 90]
Поднять хвост
Вперёд 2 Направо 90 Вперёд 3 Налево 90
Опустить хвост
Повтори 2 [Вперёд 4 Направо 90 Вперёд 2 Направо 90]
Выполняя этот алгоритм, Черепаха рисует одну за другой две фигуры. Определите, сколько точек с целочисленными координатами будут находиться внутри второй нарисованной фигуры, но не внутри первой. Точки на границах указанной области учитывать не следует.
Решение
использовать Черепаха
 алг
алг
нач
. опустить хвост
. нц 2 раз
. . вперед(7)
. . вправо (90)
. . вперед(8)
. . вправо(90)
. кц
. поднять хвост
. вперед(2)
. вправо(90)
. вперед(3)
. влево(90)
. опустить хвост
. выбрать чернила (красный)
. нц 2 раз
. . вперед(4)
. . вправо (90)
. . вперед(2)
. . вправо(90)
. кц
кон
Вторую фигуру обозначим красным цветом, чтобы не путать. Внутри красной (второй) фигуры 3 точки, но все они находятся внутри черной (первой) фигуры, а это противоречит условию. В итоге ответ 0.
Ответ 0
8. 1) Оля составляет слова перестановкой букв слова СПОРТЛОТО, оставляя только слова с двумя буквами Т рядом. Сколько различных слов может составить Оля?
Решение
from itertools import permutations
words = set()
s = 'спортлото'
for p in permutations(s):
w = ''.join(p)
if w.count('тт') == 1:
words.add(w)
print(len(words))
Ответ 6720
8. 2) Оля составляет слова перестановкой букв слова СПОРТЛОТО, оставляя только слова с различными буквами в начале и в конце. Сколько различных слов может составить Оля?
Решение
from itertools import permutations
words = set()
s = 'спортлото'
for p in permutations(s):
w = ''.join(p)
if w[0]!= w[8]:
words.add(w)
print(len(words))
Ответ 26880
8. 3) Оля составляет слова перестановкой букв слова СПОРТЛОТО, оставляя только слова с гласной в начале и/или в конце слова. Сколько различных слов может составить Оля?
Решение
from itertools import permutations
words = set()
s = 'спортлото'
for p in permutations(s):
w = ''.join(p)
![]() if w[0]== 'о' or
w[8]=='о':
if w[0]== 'о' or
w[8]=='о':
words.add(w)
print(len(words))
Ответ 17640
8. 4) Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Вот начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
Запишите слово, которое стоит на 210-м месте от начала списка.
Решение.
Заменим буквы А, О, У на 0, 1, 2(для них порядок очевиден – по возрастанию)
Выпишем начало списка, заменив буквы на цифры:
1. ААААА 1. 00000 1. 0
2. ААААО 2. 00001 2. 1
3. ААААУ 3. 00002 3. 2
4. АААОА 4. 00010 4. 3
Полученная запись есть числа, записанные в троичной системе счисления в порядке возрастания. Т.е. число 3 (третий столбец) находится в строчке 4, тогда на 210 месте будет стоять число 209 (т. к. первое число 0). Переведём число 209 в троичную систему: 2093 = 2120210. В троичной системе 209 запишется как 21202. Произведём обратную замену и получим УОУАУ.
Ответ: УОУАУ
8. 5) Все 5-буквенные слова, составленные из букв Л, Н, Р, Т, записаны в алфавитном порядке. Вот начало списка:
1. ЛЛЛЛЛ
2. ЛЛЛЛН
3. ЛЛЛЛР
4. ЛЛЛЛТ
5. ЛЛЛНЛ
Запишите слово, которое стоит на 150-м месте от начала списка.
Решение.
Заменим буквы Л, Н, Р, Т на 0, 1, 2, 3 соответственно.
Выпишем начало списка, заменив буквы на цифры:
1. ЛЛЛЛЛ 1. 00000 1. 0
2. ЛЛЛЛН 2. 00001 2. 1
3. ЛЛЛЛР 3. 00002 3. 2
4. ЛЛЛЛТ 4. 00003 4. 3
5. ЛЛЛНЛ 5.00010 5. 4
...
Полученная запись есть числа, записанные в четверичной системе счисления в порядке возрастания. Тогда на 150-м месте будет стоять число 149 (т. к. первое число 0). Переведём число 149 в четверичную систему: 14910=21114. В четверичной системе 149 запишется как 2111. Поскольку слова 5-буквенные, добавим в начале числа незначащий нуль, получим 02111. Произведём обратную замену и получим ЛРННН.
Ответ: ЛРННН.
8. 6) Все пятибуквенные слова, в составе которых могут быть только буквы Б, А, Т, Ы, Р, записаны в алфавитном порядке и пронумерованы начиная с 1.
Ниже приведено начало списка.
1. ААААА
2. ААААБ
3. ААААР
4. ААААТ
5. ААААЫ
6. АААБА
Под каким номером в списке идёт первое слово, которое не содержит ни одной буквы Ы и не содержит букв А, стоящих рядом?
Решение.
Заменим буквы на цифры следующим образом: А — 0, Б — 1, Р — 2, Т — 3, Ы — 4. Получаем список:
1. ААААА 1. 00000 1. 0
2. ААААБ 2. 00001 2. 1
3. ААААР 3. 00002 3. 2
4. ААААТ 4. 00003 4. 3
5. ААААЫ 5. 00004 5. 4
Заметим, что первое слово, не содержащее букв Ы и стоящих рядом букв А можно записать как АБАБА — это и будет первое такое слово. Используется пятибуквенный алфавит, значит, чтобы найти номер слова АБАБА, нужно найти значение числа 010105 в десятичном виде. Им является число 13010, но поскольку номер в списке на единицу больше самого числа, то остаётся добавить к получившемуся числу единицу. Получаем 131.
Ответ: 131.
8. 7) Валерия составляет 3-буквенные коды из букв В, А, Л, Е, Р, И, Я, причём буква В должна входить в код ровно один раз. Все полученные коды Валерия записала в алфавитном порядке и пронумеровала. Начало списка выглядит так:
1. ААВ
2. АВА
3. АВЕ
…
На каком месте будет записан первый код, не содержащий ни одной буквы А?
Решение.
Запишем каждую букву и соответствующую ей цифру: А — 0, В — 1, Е — 2, И — 3, Л — 4, Р — 5, Я — 6. Продолжим список кодов, пока не встретим код, не содержащий цифры 0. Будем учитывать, что в коде должна встречаться ровно одна цифра 1. Получим:
1 — 001 5 — 014 9 — 031 13 — 100 17 — 105
2 — 010 6 — 015 10 — 041 14 — 102 18 — 106
3 — 012 7 — 016 11 — 051 15 — 103 19 — 120
4 — 013 8 — 021 12 — 061 16 — 104 20 — 122
Таким образом, первый код, не содержащий ни одной буквы А, будет записан под номером 20.
Ответ: 20.
8. 8) Виктор составляет коды из букв, входящих в слово ВИКТОР. Каждая буква должна входить в код ровно один раз. Все возможные коды Виктор записывает в алфавитном порядке и нумерует. Начало списка выглядит так:
1. ВИКОРТ
2. ВИКОТР
3. ВИКРОТ
Какой код будет записан под номером 266?
Решение:
from itertools import permutations
k=0
for j in permutations ('ВИКОРТ'):
k=k+1
print(k,j)
Вывод Питона:
264 ('К', 'В', 'Т', 'Р', 'О', 'И')
265 ('К', 'И', 'В', 'О', 'Р', 'Т')
266 ('К', 'И', 'В', 'О', 'Т', 'Р')
267 ('К', 'И', 'В', 'Р', 'О', 'Т')
268 ('К', 'И', 'В', 'Р', 'Т', 'О')
Ответ: КИВОТР
12. Нахождение простых чисел
a=[2]
n=1000
for i in range(3,n+1,2):
k=0
q=int(n**0.5)+2
for j in a:
if j>q:
break
if i%j==0:
k=1
break
if k==0:
a.append(i)
print(a)
print(len(a))
8. 9) Сколько существует различных трёхзначных чисел, записанных в шестиричной системе счисления, в записи которых цифры следуют слева направо в невозрастающем порядке?
Решение
n = 0
for i in range(1,6):
for j in range(0,6):
for k in range(0,6):
if i >= j and j >= k:
n=n+1
![]() print(n)
print(n)
Ответ: 55
8. 10) Полина составляет коды из букв слова ПОЛИНА. Код должен состоять из 8 букв, любую букву можно использовать произвольное число раз или не использовать вовсе. Полина хочет, чтобы согласных в каждом коде было больше, чем гласных. Сколько кодов, удовлетворяющих этому условию, она сможет составить?
Решение
from itertools import product
count = 0
for p in product("ПОЛИНА", repeat=8):
gl = p.count('О') + p.count('И') + p.count('А')
sog = p.count('П') + p.count('Л') + p.count('Н')
if sog > gl:
count+=1
print(count)
Ответ 610173
8. 11) Определите количество шестизначных чисел, записанных в девятеричной системе счисления, в записи которых ровно одна цифра 4 и ровно две нечётные цифры.
Решение
from itertools import product
count = 0
for p in product("012345678", repeat=6):
if p.count("4") == 1 and p[0]!="0" and(p.count("1")+p.count("3") + p.count("5") + p.count("7"))==2:
count+=1
print(count)
Ответ: 53760
8. 12) Сколько существует 9-значных девятеричных чисел, в записи которых не встречается цифра 0, любые две соседние цифры имеют разную чётность, и никакая цифра не повторяется больше 3 раз?
Решение
from itertools import *
c1 = '1357'
c2 = '2468'
count = 0
for i in product(c1,c2,c1,c2,c1,c2,c1,c2,c1):
s = ''.join(i)
if s.count('1') < 4 and s.count('2') < 4 and s.count('3') < 4 and s.count('4') < 4 and s.count('5') < 4 and s.count('6') < 4 and s.count('7') < 4 and s.count('8') < 4:
count += 1
print(count * 2)
Ответ 483840
8. 13)

Решение (другой способ)
from itertools import *
c1 = '357'
c2 = '246'
c3= '0246'
count = 0
k=0
for i in product(c2,c1,c3,c1,c3):
s = ''.join(i)
if s.count('2') <= 1 and s.count('3') <= 1\
and s.count('4') <= 1 and s.count('5') <= 1\
and s.count('6') <= 1 and s.count('7') <= 1 and s.count('0')<=1:
count += 1
for i in product(c1,c3,c1,c3,c1):
s = ''.join(i)
if s.count('2') <= 1 and s.count('3') <= 1\
and s.count('4') <= 1 and s.count('5') <= 1\
and s.count('6') <= 1 and s.count('7') <= 1 and s.count('0')<=1:
k += 1
print(count+k)
Ответ 180
12. 1) Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>0)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 22>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>0)
ТО заменить (>0, 1>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой выше программе поступает строка, начинающаяся с символа «>», а затем содержащая 39 цифр «0», n цифр «1» и 39 цифр «2», расположенных в произвольном порядке.
Определите наименьшее значение n, при котором сумма числовых значений цифр строки, получившейся в результате выполнения программы, является простым числом.
Решение
n=5
s='>'+'0'*39+'1'*n+'2'*39
while '>1' in s or '>2' in s or '>0' in s:
if '>1' in s:
s=s.replace('>1','22>',1)
if '>2' in s:
s=s.replace('>2','2>',1)
if '>0' in s:
s=s.replace('>0','1>',1)
print('строка-',s)
print('n-',n)
print('сумма-',s.count('1')+s.count('2')*2)
Вывод Питон
строка- 1111111111111111111111111111111111111112222222222222222222222222222222222222222222222222>
n- 5
сумма- 137
Ответ 137
12. 2) Дана программа для редактора:
НАЧАЛО
ПОКА НЕ нашлось (00)
заменить (01, 210)
заменить (02, 3101)
заменить (03, 2012)
КОНЕЦ ПОКА
КОНЕЦ
Известно, что исходная строка начиналась с нуля и заканчивалась нулём, а между ними содержала только единицы, двойки и тройки. После выполнения данной программы получилась строка, содержащая 61 единицу, 50 двоек и 18 троек. Сколько цифр было в исходной строке?
Решение
for k1 in range(61):
![]() for k2 in range(50):
for k2 in range(50):
for k3 in range(18):
s='0' + k1*'1' + k2*'2' + k3*'3' + '0'
while '01' in s or '02' in s or '03' in s:
s = s.replace('01', '210', 1)
s = s.replace('02', '3101', 1)
s = s.replace('03', '2012', 1)
if s.count('1')==61 and s.count('2') == 50 and s.count('3') == 18:
print (k1 + k2 + k3 + 2)
Ответ: 38
Другой способ
x-01→210, y-02→3101→31210, z-03→2012→22102→22131210
![]()
Решая систему уравнений, находим x=18, y=11, z=7.
Значит, всего в исходной строке, учитывая два нуля, 18 + 11 + 7 + 2 = 38 цифр
Ответ 38
12. Дана программа для редактора:
НАЧАЛО
ПОКА нашлось (01) ИЛИ нашлось (02) ИЛИ нашлось (03)
заменить (01, 30)
заменить (02, 101)
заменить (03, 202)
КОНЕЦ ПОКА
КОНЕЦ
Известно, что исходная строка начиналась с нуля, а далее содержала только единицы, двойки и тройки. После выполнения данной программы получилась строка, содержащая 20 единиц, 10 двоек и 70 троек. Сколько единиц было в исходной строке?
Решение
for x in range(60):
for y in range(60):
for z in range(60):
s='0'+x*'1'+y*'2'+z*'3'
while '01' in s or '02' in s or '03' in s:
s=s.replace('01','30',1)
s=s.replace('02','101',1)
s=s.replace('03','202',1)
if s.count('1')==20 and s.count('2')==10 and s.count('3')==70:
print(x)
Ответ 50
12. 4) Дана программа для редактора:
НАЧАЛО
ПОКА нашлось (1111)
заменить (1111, 22)
заменить (222, 1)
КОНЕЦ ПОКА
КОНЕЦ
Известно, что исходная строка содержала больше 200 единиц и не содержала других цифр. При какой наименьшей длине исходной строки результат работы данной программы будет содержать наименьшее возможное число единиц?
Решение
Поочередно вместо n подставляем числа от 201, пока не обнаружим минимальное кол-во единиц в ответе. При 201 их 4, при 202 – 2, при 203 – 3, а при 204 – 0. Это минимум.
n=204
s='1'*n
while '1111' in s:
s=s.replace('1111','22',1)
s=s.replace('222','1',1)
print('n - ',n)
print('строка - ',s)
print('кол-во единиц - ',s.count('1'))
Вывод Питон
n - 204
строка - 22
кол-во единиц - 0
Ответ 204
14. 1) Операнды арифметического выражения записаны в системах счисления с основаниями 9 и 11: 88x4y9 + 7x44y11
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите значения x и y, при которых значение данного арифметического выражения будет наименьшим и кратно 61. Для найденных значений x и y вычислите частное от деления значения арифметического выражения на 61 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Решение
for x in range(0,9):
for y in range(0,9):
a = y*9**0 + 4*9**1 + x*9**2 + 8*9**3 + 8*9**4
g = y*11**0 + 4*11**1 + 4*11**2 + x*11**3 + 7*11**4
d = a + g
if d%61==0:
print(d//61,'x=',x,'y=',y)
Вывод Питон: 2715 x= 3 y= 4
Ответ: 2715
14. 2) Операнды арифметического выражения записаны в системе счисления с основаниями 15 и 13: 4Cx415 + x62A13
В записи чисел переменной x обозначена неизвестная цифра из алфавита десятичной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 121. Для найденного значения x вычислите частное от деления значения арифметического выражения на 121 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Решение
for x in range(0,10):
a= 4*15**0 + x*15**1 + 12*15**2 + 4*15**3
b= 10*13**0 + 2*13**1 + 6*13**2 + x*13**3
c=a+b
if c%121==0:
print (c//121,'x=',x)
Вывод Питон 234 x= 5
Ответ: 234
14. 3) Числа M и N записаны в системе счисления с основанием 9 соответственно. M = 842x59, N = 8x7259
В записи чисел переменной x обозначена неизвестная цифра из алфавита девятеричной системы счисления. Определите наименьшее значение натурального числа A, при котором существует такой x, что M + A кратно N.
Решение
for A in range (0,1001):
for x in range(0,9):
M = 8*9**4 + 4*9**3 + 2*9**2 + x*9**1 + 5*9**0
N = 8*9**4 + x*9**3 + 7*9**2 + 2*9**1 + 5*9**0
if (M+A)%N==0:
print('A=',A,'X=',x)
Вывод в Питон A= 387 X= 4
Ответ: 387
14. 4) В системе счисления с основанием p выполняется равенство
87x6 + x5x8 = y7y92
Буквами x и y обозначены некоторые цифры из алфавита системы счисления с основанием p. Определите значение числа yxxyp и запишите это значение в десятичной системе счисления.
Решение:
for p in range(10,101):
for x in range(p):
for y in range(p):
a=8*p**3 + 7*p**2 + x*p**1 + 6*p**0
![]() b=x*p**3 + 5*p**2 + x*p**1 + 8*p**0
b=x*p**3 + 5*p**2 + x*p**1 + 8*p**0
c=y*p**4+ 7*p**3 + y*p**2 + 9*p**1 + 2*p**0
if a+b==c:
d=y*p**3 + x*p**2 + x*p**1 + y*p**0
print('при p=',p,', d=',d)
Вывод Питон: при p= 12 , d= 3289
Ответ: 3289
14. 5) Дано арифметическое выражение: 4xB526 · 2x3x+1
В записи чисел переменной x обозначена неизвестная десятичная цифра. При каком значении переменной х, данное выражение, записанное в 5-ричной системе счисления, имеет сумму цифр равную 19? Если таких значений х несколько, найдите то, при котором 5-ричная запись выражения имеет наибольшее количество цифр 4. В ответе для найденного значения x укажите значение выражения в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Решение
Диапазон для х от 3 до 9 включительно, т.к. основание у второго множителя х+1 не может быть меньше 4.
for x in range(3,10):
a = 4*26**3 + x*26**2 + 11*26**1 + 5*26**0
b = 2*(x+1)**2 + x*(x+1)**1 + 3*(x+1)**0
c= a*b
p=c
k=0
while c!=0:
k=k+c%5
c=c//5
if k==19:
print('число=',p,'сумма=',k)
t=0
while p!=0:
if p%5==4:
t=t+1
p=p//5
print('кол-во 4-',t)
Вывод Питон
число= 926523 сумма= 19
кол-во 4- 2
число= 5350827 сумма= 19
кол-во 4- 0
число= 7767375 сумма= 19
кол-во 4- 3
число= 18012711 сумма= 19
кол-во 4- 2
Ответ: 7767375
Другой способ
for x in range(3, 10):
a = 4*26**3 + x*26**2 + 11*26 + 5
b = 2*(x+1)**2 + x*(x+1) + 3
c = a*b
m = []
n = c
while n != 0:
m.append(n%5)
n//=5
if sum(m) == 19:
print(m, c)
Вывод Питон
[2, 0, 3, 1, 1, 2, 2, 3, 3, 2] 5350827
[0, 0, 0, 4, 2, 0, 2, 4, 4, 3] 7767375
[1, 2, 3, 1, 0, 4, 2, 0, 1, 4, 1] 18012711
Во второй строке четверок три, поэтому это и будет ответ
Ответ: 7767375
14. 6) Дано арифметическое выражение: 3B8x117 + 2x9x317
В записи чисел переменной x обозначена неизвестная цифра из алфавита 17-ричной системы счисления. Найдите наименьшее значение переменной x, при котором запись значения этого выражения в 6-ричной системе счисления содержит ровно три цифры «5». В ответе для найденного значения x укажите значение выражения в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Решение:
for x in range(0, 17):
a = 1*17**0 + x*17**1 + 8*17**2 + 11*17**3 + 3*17**4
b = 3*17**0 + x*17**1 + 9*17**2 + x*17**3 + 2*17**4
c = a+b
n = c
k=0
while n != 0:
if n%6==5:
k=k+1
n=n//6
if k==3:
print('число-',c,'кол-во пятерок-', k)
Вывод Питон.
число- 535929 кол-во пятерок- 3
число- 535929 кол-во пятерок- 3
число- 550770 кол-во пятерок- 3
число- 550770 кол-во пятерок- 3
Минимальный среди них 535929.
Ответ: 535929
14. 7) Дано арифметическое выражение: MFx7237 + Tx7Y237
В записи чисел переменной x обозначена неизвестная цифра из алфавита 37-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 536. Для найденного значения x вычислите частное от деления значения арифметического выражения на 536 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Решение:
В этом задании заглавные буквы M, F, T, Y являются цифрами в 37-ной системе счисления. Для определения этих цифр воспользуемся Excel. В A1 и B1 числа 10 и 11, это соответствует тому, что A – 10, B – 11. Копируем числа до Y включительно.
14. 8) Операнды арифметического выражения записаны в системе счисления с основанием 16: 8569x16 + 12x4816
В записи чисел переменной x обозначена неизвестная цифра из алфавита 16-ричной системы счисления. Определите наибольшее значение x, при котором у значения данного арифметического выражения, записанного в 8-ричной системе счисления, встречается не более двух чётных цифр. Для найденного значения x запишите значение выражения в восьмеричной системе счисления. Основание системы счисления указывать не нужно.
Решение:
При команде oct(c) питон выводит ответ с символами 0о в начале, что означает 8-ная система. Поэтому нужно их отсечь [2:]. В 8-нойсистеме четными являются 0,2,4,6.
for x in range(0,16):
a = x*16**0 + 9*16**1 + 6*16**2 + 5*16**3 + 8*16**4
b = 8*16**0 + 4*16**1 + x*16**2 + 2*16**3 + 1*16**4
c = a+b
g=oct(c)
f=g[2:]
d=f.count('0')+f.count('2')+f.count('4')+f.count('6')
if d<3:
print(f,'при х=',x,'число четных=',d )
Вывод Питон
2273731 при х= 1 число четных= 2
2275735 при х= 5 число четных= 2
Максимальный 2275735
Ответ: 2275735
14. 9) Дано арифметическое выражение: 3x15x15 + 1233x51 + xx + 1x31x3 + 1x2x+1
В записи чисел переменной x обозначена неизвестная цифра. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 13. Для найденного значения x вычислите значение арифметического выражения и укажите его в ответе в системе счисления с основанием 13. Основание системы счисления в ответе указывать не нужно.
Решение:
По последнему слагаемому понятно, что нижняя граница для х это 2.
3х51 (основание второго слагаемого) нужно представить в виде k.
for x in range(2,10):
m= x*15**0 + 5*15**1 + 1*15**2 + x*15**3 + 3*15**4
k= 1*10**0 + 5*10**1 + x*10**2 + 3*10**3
n= 3*k**0 + 2*k**1 + 1*k**2
h= x**x
r= 3*10**0 + x*10**1 + 1*10**2
p= 3*r**0 + x*r**1 + 1*r**2
![]() j=
2*(x+1)**0 + x*(x+1)**1 + 1*(x+1)**2
j=
2*(x+1)**0 + x*(x+1)**1 + 1*(x+1)**2
t= m+n+h+p+j
if t%13 == 0:
print(t, 'при х=',x)
Вывод Питон 12103312 при х= 4
Это число нужно перевести в 13 вид. Можно и стандартным образом. Получится
Ответ 267A030
14. 10) Операнды арифметического выражения записаны в системе счисления с некоторым частично заданным основанием: 13132x4 – 13x4222
В записи чисел переменной x обозначена неизвестная цифра. Определите наибольшее значение x, при котором абсолютное значение данного арифметического выражения при делении на 100 даёт остаток 53. Для найденного значения x вычислите целое частное от деления абсолютного значения арифметического выражения на 100 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Решение:
for x in range(0,10):
f = 4*10**0 + x*10**1 + 2*10**2 + 3*10**3 + 1*10**4
a = 3*f**0 + 1*f**1
b = 2*22**0 + 4*22**1 + x*22**2 + 3*22**3 + 1*22**4
c = abs(a-b)
if c%100==53:
print(c//100,'при х=',x)
Вывод Питон: 2554 при х= 5
Ответ: 2554
14. 11) Значение выражения 3*3438 + 5*4912 + 715 - 49 записали в системе счисления с основанием 7 без незначащих нулей. Какая цифра чаще всего встречается в этой записи?
Решение:
for p in range(0,7):
x=3*343**8 + 5*49**12 + 7**15 - 49
k=0
while x != 0:
if x % 7 == p:
k += 1
x= x // 7
print('cc-',p,'кол-во чисел=',k)
Вывод Питон
cc- 0 кол-во чисел= 11 cc- 4 кол-во чисел= 0
cc- 1 кол-во чисел= 2 cc- 5 кол-во чисел= 0
cc- 2 кол-во чисел= 0 cc- 6 кол-во чисел= 13
cc- 3 кол-во чисел= 0 «6» встречается 13 раз.
Ответ: 6
14. 12) Значение арифметического выражения
7 · 5121912 + 6 · 641954 − 5 · 81991 − 4 · 81980 − 2022
записали в системе счисления с основанием 8. Определите количество цифр 7 в записи этого числа.
Решение:
x= 7*512**1912 + 6*64**1954 - 5*8**1991 - 4*8**1980 - 2022
d=oct(x)
d=d[2:]
print(d.count('7'))
Ответ: 3903
14. 13) Значение выражения 2 · 2168 + 4 · 3612 + 615 − 1296 записали в системе счисления с основанием 6. Сколько значащих нулей содержится в этой записи?
Решение:
s=2*216**8 + 4*36**12 + 6**15 - 1296
k=0
while s!=0:
if s%6==0:
k=k+1
s=s//6
print(k)
Ответ: 14
14. 14) Значение выражения 434 + 5 · 422 + 413 + 2 · 49 + 82 записали в системе счисления с основанием 16. Сколько разных цифр встречается в этой записи?
Решение
for p in range(0,16):
x= 4**34 + 5*4**22 + 4**13 + 2*4**9 + 82
k= 0
while x != 0:
if x % 16 == p:
k = k + 1
x= x // 16
print('кол-во=',k,'система сч.=',p)
Вывод Питон
кол-во= 12 система сч.= 0 кол-во= 1 система сч.= 8
кол-во= 1 система сч.= 1 кол-во= 0 система сч.= 9
кол-во= 1 система сч.= 2 кол-во= 0 система сч.= 10
кол-во= 0 система сч.= 3 кол-во= 0 система сч.= 11
кол-во= 1 система сч.= 4 кол-во= 0 система сч.= 12
кол-во= 2 система сч.= 5 кол-во= 0 система сч.= 13
кол-во= 0 система сч.= 6 кол-во= 0 система сч.= 14
кол-во= 0 система сч.= 7 кол-во= 0 система сч.= 15
Видно, что «0» - 12, «1» - 1, «2» - 1, «4» - 1, «5» - 2, «8» - 1. Других чисел нет. Следовательно, встречаются 0,1,2,4,5,8, т.е. 6 различных цифр.
Ответ: 6
14. 14) Операнды арифметического выражения записаны в системе счисления с основанием 158. 273x2158 + 1x390158
В записи чисел переменной x обозначена неизвестная цифра из алфавита 158-ричной системы счисления. Определите все значения x, при которых значение данного арифметического выражения кратно 73. Для каждого найденного значения x вычислите частное от деления значения арифметического выражения на 73 и укажите их сумму в ответе в десятичной системе счисления.
Решение:
k=0
for x in range(0,158):
a = 2*158**0 + x*158**1 + 3*158**2 + 7*158**3 + 2*158**4
b = 0*158**0 + 9*158**1 + 3*158**2 + x*158**3 + 1*158**4
c = a + b
if c%73==0:
k=k+c//73
print(k)
Ответ: 61978870
14. 15) Операнды арифметического выражения записаны в системе счисления с основанием 55. ZaYX55 – 2XaY55
В записи чисел переменной a обозначена неизвестная цифра из алфавита 55-ричной системы счисления. Определите наибольшее и наименьшее значение a, при котором значение данного арифметического выражения кратно 29. Для найденных значений a найдите модуль разности значений соответствующих выражений.
Решение: В Excele определяем цифровые значения для Z, Y, X.
for a in range(0,55):
n = 33*55**0 + 34*55**1 + a*55**2 + 35*55**3
m = 34*55**0 + a*55**1 + 33*55**2 + 2*55**3
r = n-m
if r%29==0:
print(r)
t=5546859-5460729
print(t)
Ответ: 86130
14. 16) Два числа
записаны в системах счисления с основаниями x и 80.
55113x, 7xx580
В записи чисел переменной x обозначены основание системы счисления первого операнда и неизвестная цифра из алфавита 80-ричной системы счисления второго операнда. Определите, сколько существует значений x, при которых указанные два числа отличаются не более, чем на 1 000 000. В ответе укажите это количество в десятичной системе счисления.
Решение:
k=0
for x in range(6,80):
a = 3*x**0 + 1*x**1 + 1*x**2 + 5*x**3 + 5*x**4
b = 5*80**0 + x*80**1 + x*80**2 + 7*80**3
c=abs(a-b)
if c<=1000000:
k=k+1
print(c,k)
Вывод Питон:
![]() 581590 1
581590 1
112702 2
407528 3
982670 4
Таких чисел 4
Ответ: 4
15. 17) Операнды арифметического выражения записаны в системах счисления с основаниями 22 и 13. x23x522 – 67y9y13
В записи чисел переменными x и y обозначены неизвестные значащие цифры из алфавитов 22-ричной и 13-ричной систем счисления соответственно. Определите значения x, y, при которых значение данного арифметического выражения кратно 57. Для найденных значений x, y вычислите частное от деления значения арифметического выражения на 57 и укажите его в ответе в десятичной системе счисления. Если можно выбрать x, y не единственным образом, возьмите ту пару, в которой сумма значений x и y меньше. Основание системы счисления в ответе указывать не нужно.
Решение:
for x in range(1,22):
for y in range(0,13):
a = 5*22**0 + x*22**1 + 3*22**2 + 2*22**3 + x*22**4
b = y*13**0 + 9*13**1 + y*13**2 + 7*13**3 + 6*13**4
c = a - b
if c%57==0:
print(c//57,'x+y=',x+y)
Вывод Питон:
25871 x+y= 14
54639 x+y= 22
58773 x+y= 15
83407 x+y= 30
Минимальная сумма х и у это 14.
Ответ: 25871
14. 18) Операнды арифметического выражения записаны в системах счисления с основаниями 15 и 17. 123x515 + 67y917
В записи чисел переменными x и y обозначены неизвестные цифры из алфавитов 15-ричной и 17-ричной систем счисления соответственно. Определите значения x, y, при которых значение данного арифметического выражения кратно 131. Для найденных значений x, y вычислите частное от деления значения арифметического выражения на 131 и укажите его в ответе в десятичной системе счисления. Если можно выбрать x, y не единственным образом, возьмите ту пару, в которой значение y меньше. Основание системы счисления в ответе указывать не нужно.
Решение:
for x in range (0,15):
for y in range(0,17):
a = 5*15**0 + x*15**1 + 3*15**2 + 2*15**3 + 1*15**4
b = 9*17**0 + y*17**1 + 7*17**2 + 6*17**3
c = a + b
if c%131==0 and y<x:
print(c//131, 'x=',x,'y=',y)
Вывод Питон: 686 x= 11 y= 8
Ответ: 686
14. 19) Операнды арифметического уравнения записаны в разных системах счисления. 19x61₁₂ + 3393x₁₇ = 60x05₁₅
В записи чисел переменной x обозначена неизвестная цифра. Определите наименьшее значение x, при котором данное уравнение верно. В ответе укажите значение правой части уравнения в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Решение:
for x in range (0,12):
a = 1*12**0 + 6*12**1 + x*12**2 + 9*12**3 + 1*12**4
b = x*17**0 + 3*17**1 + 9*17**2 + 3*17**3 + 3*17**4
c = 5*15**0 + 0*15**1 + x*15**2 + 0*15**3 + 6*15**4
if a+b==c:
print(c, 'x=',x)
Вывод Питон: 305330 x= 7
Ответ: 305330
14. 20) Значение выражения 52026 + 7·51013 + 107 – X записали в системе счисления с основанием 6. Определите минимальное натуральное значение X, при котором цифр 5 в такой записи на 28 больше, чем цифр 0.
Решение:
for x in range (1,10):
s = 5**2026 + 7*5**1013 + 107 - x
k=0
j=0
while s!=0:
if s%6==5:
k=k+1
if s%6==0:
j=j+1
s=s//6
if k-j==28:
print('k=',k,'j=',j,'k-j=',k-j,'x=',x)
break
Вывод Питон: k= 296 j= 268 k-j= 28 x= 5
Ответ: 5
14. 21) Значение выражения 4·83032 + 3·161956 + 870 записали в системе счисления с основанием 7. Определите разность между суммой цифр "3" и суммой цифр "1" в записи этого числа.
Решение:
s = 4*8**3032 + 3*16**1956 + 870
k=0
j=0
while s!=0:
if s%7==3:
k=k+1
if s%7==1:
j=j+1
s=s//7
print('сумма 3=',3*k,'сумма 1=',j,'разница=',3*k-j)
Вывод Питон: сумма 3= 1362 сумма 1= 447 разница= 915
Ответ: 915
14. 22) Значение выражения 981 + 27729 – 4 записали в системе счисления с основанием 9. Затем все нули заменили на максимальную цифру в этой записи. Определите, сколько раз встречается максимальная цифра в этой записи после преобразования.
Решение:
for x in range(0,9):
s = 9**81 + 27**729 - 4
k=0
while s!=0:
if s%9==x:
k=k+1
s=s//9
print('цифра=',x, 'кол-во=',k)
Вывод Питон:
цифра= 0 кол-во= 1012 цифра= 3 кол-во= 1 цифра= 6 кол-во= 0
цифра= 1 кол-во= 0 цифра= 4 кол-во= 0 цифра= 7 кол-во= 0
цифра= 2 кол-во= 0 цифра= 5 кол-во= 1 цифра= 8 кол-во= 80
«0» - 1012, максимальная цифра, т.е. «8» - 80 раз встречается. Следовательно, 1012 ноликов заменились на восьмерки. В итоге, 1012+80=1092 максимальных цифр.
Ответ: 1092
14. 23) Значение выражения 1981 + 23709 – 4 записали в системе счисления с основанием 9. Определите количество комбинаций цифр 8# в этой записи, где # – любая цифра от 1 до 7.
Решение:
s = 19**81 + 23**709 - 4
n=''
while s!=0:
n = str(s%9) + n
s=s//9 d=n.count('81')+n.count('82')+n.count('83')+n.count('84')+n.count('85')+n.count('86')+n.count('87')
print(d)
Ответ: 73
14. 24) Значение выражения (6425 + 410) – (1620 + 323) записали в системе счисления с основанием 4. В каком разряде четверичной записи числа при просмотре справа налево впервые встречается цифра 2?
Решение:
s = (64**25 + 4**10)-(16**20 + 32**3)
n=''
while s!=0:
![]() n=str(s%4)+n
n=str(s%4)+n
s=s//4
print(n)
Вывод Питон:
333333333333333333333333333333333330000000000000000000000000000003320000000
Двойка справа встречается впервые 8, а это 7 разряд (т.е., самая крайняя цифра, это нулевой разряд, предпоследняя – это первый и т.д.)
Ответ: 7
14. 25) Переведите выражение 1644*1630 – (325 *(840 - 832)*(1614 - 324)) в 15-ную систему и определите 7 цифру слева направо.
Решение
Если переведем предыдущим способом, мы будем путать, где подобные цифры: 10 это подразумевается А или 1 и 0. Поэтому в строке для определения n внесем еще пустоту ‘’.
s = 16**44*16**30-(32**5*(8**40-8**32)*(16**14-32**4))
n=''
while s!=0:
n=str(s%15)+' '+n
s=s//15
n=n.replace('10','a',1)
n=n.replace('11','b',1)
n=n.replace('12','c',1)
n=n.replace('13','d',1)
n=n.replace('14','e',1)
print(n)
Вывод Питона: 7 d 9 2 7 9 d 3 1 2 3 d 0 e 0 9 1 4 2 8 1 8 b e 5 0 0 d 9 a c e 6 c b 0 6 4 4 2 6 b 6 b e b 8 8 7 8 0 8 2 8 b 9 7 8 9 a d a c 0 a 1 a c b 9 e 2 5 2 e 1
Ответ: d
14. 26) Значение выражения (5300 • 15100) – (2550 + 125100) записали в системе счисления с основанием 5. Запишите в ответ сумму всех цифр пятеричной записи числа, исключая четверки.
Решение:
s = (5**300*15**100)-(25**50+125**100)
k=0
while s!=0:
if s%5!=4:
k=k+s%5
s=s//5
print(k)
Ответ: 83
14. 27) Значение выражения 8118 – (818 – 1)∙((8 + 1)8 + 1) / 8 – 8 записали в системе счисления с основанием 3. Найдите количество единиц в этой записи.
Решение:
В задании есть деление. Нужно делить цело, т.е. //
s = 81**18 - (81**8-1)*((8+1)**8+1)//8-8
k=0
while s!=0:
if s%3==1:
k=k+1
s=s//3
print(k)
Ответ: 15
14. 28) Значение выражения 41103 + 3∙41444 – 2∙4144 + 66 записали в системе счисления с основанием 4. Найдите сумму цифр получившегося числа и запишите её в ответе в десятичной системе счисления.
Решение:
s = 4**1103 + 3*4**1444 - 2*4**144 + 66
k=0
while s!=0:
k=k+s%4
s=s//4
print(k)
Ответ: 2882
14. 29) Чему равно наименьшее основание позиционной системы счисления x, при котором 225x = 405y? Ответ записать в виде целого числа.
Решение:
for x in range(6,11):
for y in range(6,11):
a = 5*x**0 + 2*x**1 + 2*x**2
b = 5*y**0 + 0*y**1 + 4*y**2
if a==b:
print(x)
break
Ответ: 8
15.1) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наибольшего натурального числа А формула
(A < 50) ∧ (¬ДЕЛ(x, А) → (ДЕЛ(x, 10) → ¬ДЕЛ(x, 12)))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
Решение:
Т.к. нужно найти наибольшее значение, то в range для a берем обратный отсчет с шагом -1. break покажет только первое число, оно и будет наибольшим. В строке for x in range(1,1001): значений х ровно 1000 штук, от 1 до 1000, без 1001, поэтому k равняется 1000.
for a in range(1000, 0, -1):
k = 0
for x in range(1,1001):
if (a < 50) and ((x%a!=0)<=((x%10==0)<=(x%12!=0))):
k = k + 1
if k == 1000:
print(a)
break
Ответ: 30
15. 2) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наименьшего натурального числа А формула
ДЕЛ(A, 45) ∧ (ДЕЛ(750, x) → (¬ДЕЛ(A, x) → ¬ДЕЛ(120, x)))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
Решение:
Т.к. нужно найти наименьшее значение, то в range для a берем прямой отсчет с шагом 1 (по умолчанию шаг 1 не пишут). break покажет только первое число, оно и будет наименьшим. В строке for x in range(1,1001): значений х ровно 1000 штук, от 1 до 1000, без 1001, поэтому k равняется 1000.
for a in range(1,1001):
k = 0
for x in range(1,1001):
if (a%45==0) and ((750%x==0) <= ((a%x!=0) <= (120%x!=0))):
k = k + 1
if k == 1000:
print(a)
break
Ответ: 90
15. 3) Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула
x & 29 ≠ 0 → (x & 17 = 0 → x & А ≠ 0)
тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?
Решение:
for a in range(0, 1000):
k = 0
for x in range(0, 1000):
if (x & 29 != 0) <= ((x & 17 == 0) <= (x & a != 0)):
k =k+ 1
if k == 1000:
print(a)
break
Ответ: 12
15. 4) Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 12&6 = 11002&01102 = 01002 = 4.
Для какого наибольшего целого числа А формула
х&А ≠ 0→ (x&10 = 0 → х&3≠ 0)
тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?
Решение:
for a in range(1000,0,-1):
k = 0
for x in range(0, 1000):
if (x&a!=0)<=((x&10==0)<=(x&3!=0)):
k =k+ 1
![]() if k == 1000:
if k == 1000:
print(a)
break
Ответ: 11
15. 5) Для какого наибольшего целого числа А формула
((x ≤ 9) →(x ⋅ x ≤ A)) ⋀ ((y ⋅ y ≤ A) → (y ≤ 9))
тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?
Решение:
for a in range(300, 1, -1):
k = 0
for x in range(0, 300):
for y in range(0, 300):
if ((x <= 9) <= (x * x <= a)) and ((y*y <= a) <= (y <= 9)):
k += 1
if k == 90_000:
print(a)
break
Ответ: 99
15. 6) На числовой прямой задан отрезок A. Известно, что формула
((x ∈ A) → (x2 ≤ 81)) ∧ ((y2 ≤ 36) → (y ∈ A))
тождественно истинна при любых вещественных x и y. Какую наименьшую длину может иметь отрезок A?
Решение:
a = set()
def f(x,a):
return ((x in a) <= (x**2 <= 81)) and ((x**2 <= 36) <= (x in a))
for x in range(-1000,1000):
if not f(x,a):
a.add(x)
print(len(a) - 1)
Ответ: 12
15. 7) Для какого наибольшего целого неотрицательного числа A выражение
(x > A) ∨ (y > A) ∨ (2y + x < 110)
тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y?
Решение:
for A in range(300, -1, -1):
k = 0
for x in range(300):
for y in range(300):
if (x > A) or (y > A) or (2 * y + x < 110):
k += 1
if k == 90_000:
print(A)
break
Ответ: 36
15. 8) На числовой прямой даны два отрезка: P = [10, 29] и Q = [13, 18].
Укажите наибольшую возможную длину отрезка A, для которого выражение
((x ∈ A) → (x ∈ P)) ∨ (x ∈ Q)
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
Решение:
p=[int(i) for i in range(10,30)]
q=[int(i) for i in range(13,19)]
a=[int(i) for i in range(10,30)]
for x in range(1,100):
if not(((x in a)<=(x in p)) or(x in q)):
a.remove(x)
print(len(a)-1)
Ответ: 19
15. 9) Обозначим через ТРЕУГ(n, m, k) утверждение «существует невырожденный треугольник с длинами сторон n, m, k».
Для какого наибольшего натурального числа A формула
((ТРЕУГ(x, 10, 20) → (¬(МАКС(x, 8) > 24))) = ¬(ТРЕУГ( 3, A, x)))
Решение:
def t(n,m,k):
return max(n,m,k) < n + m + k - max(n,m,k)
def f(A,x):
return t(x,10,20) <= (not((max(x,8) > 24)) == (not t(3,A,x)))
for A in range(1000):
if all (f(A,x) for x in range(1000)):
print(A)
Ответ: 27
16. 1) Алгоритм вычисления значения функции F(n), где n — целое число, задан следующими соотношениями:
F(n) = n, если n<9
F(n)=F(n mod 9) + F(n div 9), если n>=9.
Определите количество значений n на отрезке [4 · 620; 5 · 620], для которых F(n)=121
Решение:
from functools import *
def f(n, b):
# граничное значение в b-ичной сс
a = []
while n > 0:
a = [n % b] + a
n //= b
@cache
def g(s, l, fl):
# если последовательность нужной длины, проверяем, что сумма нам подходит,
# и выходим из рекурсии.
if l == 0: return s == 121
# проверяем ограниченные подпоследовательности большей длины
return sum(g(s+x, l-1, fl and (x == a[-l])) for x in range([b, a[-l]+1][fl]))
return g(0, len(a), 1)
# ответ - разность между количеством подходящих чисел на отрезке [1; 5*6^20] и полуинтервале [1; 4*6^20).
print(f(5*6**20, 9) - f(4*6**20-1, 9))
Ответ: 194257368
16. 2) Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(n) = n при n > 2024;
F(n) = n · F(n + 1), если n ≤ 2024.
Чему равно значение выражения F(2022) / F(2024)?
Решение:
Найдем значение F(2022): F(2022) = 2022 · F(2023) = 2022 · 2023 · F(2024).
То есть значение выражения равно:
![]()
Ответ: 4090506
23. 1) Исполнитель преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья — умножает на 3.
Программа для исполнителя — это последовательность команд. Сколько существует программ, которые преобразуют исходное число 1 в число 15, и при этом траектория вычислений содержит число 10?
Решение:
def f(x, y):
if x > y:
return 0
if x == y:
![]() return 1
return 1
else:
return f(x + 1, y) + f(x + 2, y) + f(x * 3, y)
print(f(1, 10) * f(10, 15))
Ответ: 672
23. 2) Исполнитель Увеличитель преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Вычти 1;
2. Найди целую часть от деления на 2.
Первая из них число на экране уменьшает на 1, вторая заменяет число на экране на целую часть от деления числа на 2.
Программа для исполнителя — это последовательность команд.
Сколько существует программ, для которых при исходном числе 78 результатом является число 4, и при этом траектория вычислений содержит число 16?
Решение:
def f(x, y):
if x < y:
return 0
if x == y:
return 1
else:
return f(x - 1, y) + f(x // 2, y)
print(f(78, 16) * f(16, 4))
Ответ: 1232
23. 3) Исполнитель НечетМ преобразует число на экране. У исполнителя НечетМ две команды, которым присвоены номера:
1. прибавь 1
2. сделай нечётное
Первая из этих команд увеличивает число x на экране на 1, вторая переводит число x в число 2x+1. Например, вторая команда переводит число 10 в число 21. Программа для исполнителя НечетМ – это последовательность команд. Сколько существует таких программ, которые число 1 преобразуют в число 27, причём траектория вычислений не содержит число 26?
Решение:
def f(x, y):
if x > y or x == 26:
return 0
if x == y:
return 1
else:
return f(x + 1, y) + f(x * 2 + 1, y)
print(f(1,27))
Ответ: 13
23. 4) Исполнитель Фибо преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2.
Программа для исполнителя Фибо — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 3 в число 20 и при этом траектория вычислений содержит число 9 и не содержит числа 15?
Решение:
def f(x, y):
if x > y or x == 15:
return 0
if x == y:
return 1
else:
return f(x + 1, y) + f(x + 2, y)
print(f(3, 9) * f(9, 20))
Ответ: 520
23. 5) Исполнитель М17 преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 3
Первая из них увеличивает число на экране на 1, вторая увеличивает его на 2, третья умножает на 3. Программа для исполнителя М17 – это последовательность команд. Сколько существует таких программ, которые преобразуют исходное число 2 в число 12 и при этом траектория вычислений программы содержит числа 8 и 10? Траектория должна содержать оба указанных числа.
Решение:
def f(x, y):
if x > y:
return 0
if x == y:
return 1
else:
return f(x + 1, y) + f(x + 2, y) + f(x * 3, y)
print(f(2, 8) * f(8, 10) * f(10, 12))
Ответ: 60
25. 1) Маска числа — это последовательность цифр, в которой могут встречаться специальные символы «?» и «*». Символ «?» означает ровно одну произвольную цифру, символ «*» означает произвольную (в том числе пустую) последовательность цифр.
Пример. Маске 123*4?5 соответствуют числа 123405 и 12376415. Найдите все натуральные числа, не превышающие 1010, которые соответствуют маске 3?2258*4 и при этом без остатка делятся на 2024.
В ответе запишите все найденные числа в порядке возрастания.
Решение
from fnmatch import *
for x in range(0, 10**10, 2024):
if fnmatch(str(x), '3?2258*4'):
print(x)
Ответ:
3422584
352258984
3022582904
3122588744
3222584464
3322580184
3422586024
3522581744
3622587584
3722583304
3822589144
3922584864
25. 2) Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы:
— символ «?» означает ровно одну произвольную цифру;
— символ «*» означает любую последовательность цифр произвольной длины; в том числе «*» может задавать и пустую последовательность.
Например, маске 123*4?5 соответствуют числа 123405 и 12300405.
Найдите все натуральные числа, не превосходящие 109, для которых выполнены все условия:
— соответствуют маске *31*65?;
— делятся на 31 и 2031 без остатка;
— количество делителей числа является результатом любой степени двойки.
В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, справа от каждого числа их частное от деления на 2031.
Решение:
from fnmatch import *
for x in range(0,10**9, 31):
if fnmatch(str(x), '*31*65?') and x%2031==0:
k=0
for y in range(1,x+1):
if x%y==0:
k=k+1
print(k,x,x//2031)
Вывод Питон
60 31228656 15376
64 53831655 26505
96 265317654 130634
96 310523652 152892
64 333126651 164021
48 431597655 212505
32 512313657 252247
32 647931651 319021
32 831966654 409634
Среди выводов нас устраивают такие, у которых первое число к равняется 32, 64, т.е. 2 в какой-то степени.
Ответ:
53831655 26505
333126651 164021
512313657 252247
![]() 647931651 319021
647931651 319021
831966654 409634
25. 3) Среди натуральных чисел, не превышающих 109, найдите все числа, соответствующие маске 12345?7?8, делящиеся на число 23 без остатка.
В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце — соответствующие им результаты деления этих чисел на 23.
Решение:
from fnmatch import *
for x in range(0,10**9,23):
if fnmatch(str(x), '12345?7?8'):
print(x, x//23)
Ответ:
123450798 5367426
123451718 5367466
123453788 5367556
123454708 5367596
123456778 5367686
123459768 5367816
25. 4) Пусть M — сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей у числа нет, то значение M считается равным нулю.
Напишите программу, которая перебирает целые числа, бо́льшие 700 000, в порядке возрастания и ищет среди них такие, для которых значение M оканчивается на 8. Выведите первые пять найденных чисел и соответствующие им значения M.
Формат вывода: для каждого из пяти таких найденных чисел в отдельной строке сначала выводится само число, затем — значение М.
Строки выводятся в порядке возрастания найденных чисел.
Количество строк в таблице для ответа избыточно.
Решение:
for x in range(700001,700040):
for y in range(2,x):
if x%y==0:
print(x,x//y)
print('')
Вывод Питон:
Питон группами выводит пары чисел: x и x//y. Первое – само число, второе – его целый делитель. К примеру, когда число 700002, максимальный делитель – это 350001. А минимальный – это 2. Их сумма, М=350003, заканчивается на 3, а не на 8, не подходит. Рассматривая и проверяя числа по группам, суммируя максимальное и минимальное, находим
Ответ:
700005 233338
700007 100008
700012 350008
700015 140008
700031 24168
25. 5) Пусть M — сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей у числа нет, то считаем значение M равным нулю.
Напишите программу, которая перебирает целые числа, большие 452 021, в порядке возрастания и ищет среди них такие, для которых значение M при делении на 7 даёт в остатке 3. Вывести первые 5 найденных чисел и соответствующие им значения M.
Формат вывода: для каждого из 5 таких найденных чисел в отдельной строке сначала выводится само число, затем — значение М. Строки выводятся в порядке возрастания найденных чисел.
Например, для числа 20 М = 2 + 10 = 12, остаток при делении на 7 не равен 3; для числа 21 М = 3 + 7 = 10, остаток при делении на 7 равен 3.
Количество строк в таблице для ответа избыточно.
Решение:
for x in range(452022,452070):
for y in range(2,x):
if x%y==0:
s=x//y
print('x=',x,'s=',s)
print('')
Вывод Питон:
Питон группами выводит пары чисел: x и s=x//y. Первое – само число, второе – его целый делитель. К примеру, когда число 452022, максимальный делитель – это 226011. А минимальный – это 2. Их сумма, М=452024. Это число при делении на 7 должен давать остаток 3. Проверим эти пары в новом коде питона.
max=226011
min=2
if (max+min)%7==3:
print(max+min)
Первая пара не подошла. Так проверяем последующие пары, пока не получим 5 значений.
Другой способ:
def div(x):
d = set()
for i in range(2,int(x**0.5)+1):
if x%i==0:
d.add(i)
d.add(x//i)
return sorted(d)
for x in range(452022,452121):
d = div(x)
if len(d)>1:
m = d[0]+d[-1]
if m%7==3:
print(x,m)
Ответ:
452025 150678
452029 23810
452034 226019
452048 226026
452062 226033
25. 6) Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [185 311; 185 330], числа, имеющие ровно четыре различных натуральных делителя. Для каждого найденного числа запишите эти четыре делителя в четыре соседних столбца на экране с новой строки. Делители в строке должны следовать в порядке возрастания.
Например, в диапазоне [12; 14] ровно четыре различных натуральных делителя имеет число 14, поэтому для этого диапазона вывод на экране должна содержать следующие значения: 1 2 7 14
Решение:
for x in range (185311,185331):
for y in range(1,x+1):
if x%y==0:
print(x,x//y)
print('')
Вывод Питон:
Программа выводит все натуральные делители чисел группами. Среди них ищем группу, состоящую их 4 пар.
Ответ:
1 2 92657 185314
1 47 3943 185321
1 241 769 185329
25. 7) Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [210 235; 210 300], числа, имеющие ровно четыре различных натуральных делителя, не считая единицы и самого числа. Для каждого найденного числа запишите эти четыре делителя в четыре соседних столбца на экране с новой строки. Делители в строке должны следовать в порядке возрастания.
Например, в диапазоне [10; 16] ровно четыре различных натуральных делителя имеет число 12, поэтому для этого диапазона вывод на экране должна содержать следующие значения: 2 3 4 6
Решение:
Т.к. здесь 1 и само число считать нельзя, то для у range будет немного другим
for x in range (210235,210301):
for y in range(2,x):
if x%y==0:
print(x,x//y)
print('')
Вывод Питон:
Программа выводит все натуральные делители чисел группами. Среди них ищем группу, состоящую их 4 пар.
Ответ:
2 4 52561 105122
2 4 52564 105134
2 4 52571 105142
25. 8) Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [245 690; 245 756] простые числа. Выведите на экран все найденные простые числа в порядке возрастания, слева от каждого числа выведите его порядковый номер в последовательности. Каждая пара чисел должна быть выведена в отдельной строке.
Например, в диапазоне [5; 9] ровно два различных натуральных простых числа — это числа 5 и 7, поэтому для этого диапазона вывод на экране должна содержать следующие значения: 1 5 3 7
Примечание. Простое число — натуральное число, имеющее ровно два различных натуральных делителя — единицу и самого себя.
Решение:
Выведем у каждого числа все натуральные делители. Простые числа, у которых всего лишь 2 делителя, само число и 1, и будут ответом на вопрос. При этом будем указывать их порядковый номер.
k=0
for x in range(245690,245757):
k=k+1
for y in range(1,x+1):
if x % y == 0:
print(k,x,x//y)
print('')
Ответ:
22 245711
30 245719
34 245723
52 245741
58 245747
64 245753
25. 9) Пусть M(N) — пятый по величине делитель натурального числа N без учёта самого числа и единицы. Например, M(1000) = 100.
Если у числа N меньше 5 различных делителей, не считая единицы и самого числа, считаем, что M(N) = 0.
Найдите 5 наименьших натуральных чисел, превышающих 300 000 000, для которых M(N) > 0. В ответе запишите найденные значения M(N) в порядке возрастания соответствующих им чисел N.
Примечание. Пятый по величине делитель — пятый делитель из пяти наибольших делителей числа. Т. е. для числа 1000 пять наибольших делителей, не считая единицы и самого числа — 500, 250, 200, 125, 100, пятый по величине — 100.
Решение:
Будем искать все делители у первых чисел, превышающих 300 000 000. Если их будет пять или больше, запишем в ответ пятый по счету.
for x in range (300000001,300000010):
for y in range(2,x):
if x%y==0:
print(x,x//y)
print('')
Первое и второе число, меньше пяти делителей. А вот третье, пять уже есть. Пятое число 17. В четвертом числе пятый делитель 1119403. В пятом числе, пятый делитель – 151. В шестом числе пятый делитель 16666667. В седьмом числе пятый делитель 27272728
Ответ:
17
1119403
151
16666667
27272728
25. 10) Пусть M(N) — сумма двух наибольших различных натуральных делителей натурального числа N, не считая самого числа и единицы. Если у числа N меньше двух таких делителей, то M(N) считается равным 0.
Найдите 5 наименьших натуральных чисел, превышающих 11 000 000, для которых 0 < M(N) < 10 000. В ответе запишите найденные значения M(N) в порядке возрастания соответствующих им чисел N.
Решение:
Судя по логике, чтобы два наибольших делителя в сумме дали число меньше 10000, оно не должно быть четным. К примеру, 11000002 при делении на два, даст число 5500001, т.е. явно больше, чем 10000. Поэтому, чтобы, меньше было переборов, четные числа рассматривать не будем. В range укажем шаг 2.
for x in range (10999999,11000350,2):
for y in range(2,x):
if x%y==0:
print(x,x//y)
print('')
Вывод питона:
Первое число, у которых максимальные делители в сумме дают меньше, чем 10000, это 11000047, 7129+1543=8672. Следующее число 11000147, 6761+1627=8388, далее 11000267, 6949+1583=8532, далее 11000317, 4703+2339=7042, далее 11000323, 5281+2083=7364.
Ответ:
8672
8388
8532
7042
7364
25. 11) Пусть M(N) — произведение 5 наименьших различных натуральных делителей натурального числа N, не считая единицы. Если у числа N меньше 5 таких делителей, то M(N) считается равным нулю.
Найдите 5 наименьших натуральных чисел, превышающих 500 000 000, для которых 0 < M(N) < N. В ответе запишите найденные значения M(N) в порядке возрастания соответствующих им чисел N.
Решение:
Будем находить все делители чисел, кроме 1 и самого числа. Наименьшие 5 из них перемножим. Если это число меньше N, то его в ответ.
for x in range (500000001,500000020):
for y in range(2,x):
if x%y==0:
print(x,x//y)
print('')
Вывод Питона:
Перемножим последние пять делителей первого числа на калькуляторе.
2949*983*1129*43*3=48 240 045 747, т.е. намного больше 500 000 001. Таким образом будем искать те, которые меньше N. Первое число, которое удовлетворяет условию, это 500 000 004. Минимальные делители 7*6*4*3*2=1008, это меньше 500 000 004. Дальше, 500 000 006, делители 79*47*22*11*2=1 797 092, меньше 500 000 006. Далее 500 000 007, делители 309*103*39*13*3=48 408 867, меньше 500 000 007. Далее, 500 000 010, делители 10*6*5*3*2=1800, меньше 500 000 010, далее 500 000 013, делители 69*27*23*9*3=1 156 923, меньше 500 000 013.
Ответ:
1008
1797092
48408867
1800
1156923
25. 12) Рассмотрим произвольное натуральное число, представим его всеми возможными способами в виде произведения двух натуральных чисел и найдём для каждого такого произведения разность сомножителей. Например, для числа 16 получим: 16 = 16*1 = 8*2 = 4*4, множество разностей содержит числа 15, 6 и 0. Найдите все натуральные числа, принадлежащие отрезку [2 000 000; 3 000 000], у которых составленное описанным способом множество разностей будет содержать не меньше трёх элементов, не превышающих 115. В ответе перечислите найденные числа в порядке возрастания.
Решение:
for x in range(2000000,3000001):
k=0
h=x**0.5
for y in range (2,round(h)):
if x%y==0:
if(abs(x/y)-y)<=115:
k=k+1
if k>2:
print(x)
25. 13) Найдите все натуральные числа, принадлежащие отрезку [45 000 000; 50 000 000], у которых ровно пять различных нечётных делителей (количество чётных делителей может быть любым). В ответе перечислите найденные числа в порядке возрастания.
Решение:
primes = set()
def prime(n):
for i in range(2, int(n**0.5) + 1):
if n % i == 0:
return False
return True
for i in range(3, int(50000000**0.25) + 1):
if prime(i):
primes.add(i)
for i in range(45000000, 50000001):
p = i
while p % 2 == 0:
p //= 2
if int(p**0.25) in primes and (int(p**0.25))**4 == p:
print(i)
Ответ:
45212176
45265984
47458321
48469444
5. 1) Алгоритм получает на вход натуральное число N и строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. В конец двоичной записи добавляется двоичный код остатка от деления числа N на 4.
3. Результатом работы алгоритма становится десятичная запись полученного числа R.
Пример 1. Дано число N = 13. Алгоритм работает следующим образом.
1. Строим двоичную запись: 1310 = 11012.
2. Остаток от деления 13 на 4 равен 1, добавляем к двоичной записи цифру 1, получаем 110112 = 2710.
3. Результат работы алгоритма R = 27.
Пример 2. Дано число N = 14. Алгоритм работает следующим образом.
1. Строим двоичную запись: 1410 = 11102.
2. Остаток от деления 14 на 4 равен 2, добавляем к двоичной записи цифры 10 (102 = 210), получаем 1110102 = 5810.
3. Результат работы алгоритма R = 58.
Назовём доступными числа, которые могут получиться в результате работы этого алгоритма. Например, числа 27 и 58 — доступные. Определите количество доступных чисел, принадлежащих отрезку [1 100 000 000; 1 987 653 210].
Решение.
Возможные остатки от деления числа на 4 это: 0,1,2,3.
Рассмотрим какие цифры будут на конце чисел, при делении на 4 дающие остаток 0,1,2 или 3.
Остаток 0 при делении на 4 дадут числа, двоичная запись которых заканчивается на 00, добавляем остаток 0. В результате автомата доступное число будет оканчиваться на 000. Следовании при делении на 8 должен быть остаток 0.
Остаток 1 при делении на 4 дадут числа, двоичная запись которых заканчивается на 01, добавляем остаток 1. В результате автомата доступное число будет оканчиваться на 011. Следовании при делении на 8 должен быть остаток 3.
Остаток 2 при делении на 4 дадут числа, двоичная запись которых заканчивается на 10, добавляем остаток 2 (10 в в двоичной записи). В результате автомата доступное число будет оканчиваться на 1010. Следовании при делении на 16 должен быть остаток 10.
Остаток 3 при делении на 4 дадут числа, двоичная запись которых заканчивается на 11, добавляем остаток 3 (11 в двоичной записи). В результате автомата доступное число будет оканчиваться на 1111. Следовании при делении на 16 должен быть остаток 15
Посчитаем доступные числа.
КОД
count = 0
for x in range(1_100_000_000, 1_987_653_210+1):
if x%16==10 or x%16==15 or x%8==0 or x%8==3:
count += 1
print(count)
Вывод Питона:
332869954
5. 2) Алгоритм получает на вход натуральное число N и строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. В конец двоичной записи добавляется двоичный код остатка от деления числа N на 4.
3. Результатом работы алгоритма становится десятичная запись полученного числа R.
Назовем доступными числа, которые могут получиться в результате работы этого алгоритма.
Какое наибольшее количество доступных чисел может быть на отрезке, содержащем 49 натуральных чисел?
Решение:
k=0
for x in range(0,49):
if x%8==0 or x%8==3 or x%16==10 or x%16==15:
k=k+1
print(k)
Ответ: 19
Если в range укажем другой диапазон, к примеру (1,50), то ответ получится 18, а это не максимальное число
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.