1-мысал. З-ке есе.тйк барлык eki тацбалы сандардыц косындысын ЕСЕПТЕР табу керек.

Ш е ш у i. ат —12 жене а =99 болатыны 6e.wiJIi. Онда п-дј аныктау

Арифметикалык прогрессияныц алгашкы 1 О MYLueciHiH косын25

керек. а (+3) формуласы бойынша

1

99=12+(n—1)3 п=ЗО. ОсыдагО

5.2. Геометрияльщ прогрессияныц алгашкы п мушесћбц косындысы

EHlIi геометриялык прогрессиянын алгашкы п косындысыныц формуласын корытып шыгарамыз. Айтальщ, Щ, Ф, а геометриялык прогрессияныц алгашкы п мушесђ ал оныц eceJIiI'i болсын. Егер геометриялык прогрессияныц алгашкы п мушесй}йц КОСЫНДЫСьпО аркылы белгћесек, онда,9 =а + а +...+а +а тещй-

дысын табьщдар:

252.   Геометрияльщ прогрессияныц алгашкы 5 MYIIIeciHiH косындысын табьщдар:

                   1                            1

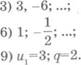   1) (61=8, q=j;    2) Ьт=5ОО, q=;;

       4) 54; 36; ...;             5) -32; 16; ...;

       —4; q=3;          

йнен,           ф- ¹ формуласын ескере отырып,

тендћћ аламыз. (4) тещјктен (5) тецјйктй азайту аркылы Sn—qS =

—ајф немесе

(6) формуласын аламыз. Мунда (7+1 болуы керек.

2-мысал. Геометрияльщ прогрессия упйн S3=9, ал болса, онда * о-ды табу керек.

Ш е ш у i. (6) формула бойынша

              ¹         =-63

1—q

Осыдан тары да (6) формула бойынша

                                                   10   3(1-20)

-1023.

                                 1-(-2)         з

[П 1. Арифметикальщ прогрессияньщ алгашкы п мушес41бц косындысыньщ  «формулаёын эка.зып, делелдецдер. 2. Геометриялык прогрессиянын алгашкы п косындысыныц формуласын жазып, далелдецдер.

253.   {ап} арифметика.лык прогрессиясыньщ алгашкы 15 мушесћйц косындысын табьщдар:

          1) (15=27, (127=60;                               

254.   {bn} геометриялык прогрессиясыныц алгашкы 6 мушесй-йц косындысын табьщдар:

                            2) ьв='25, 68=9;

       3) 61=125, ьз=5•,                         4) 66-1,        -100.

255.   Жалпы формуласымен бер[лген тйзбект1ц арифметикалык прогрессия болатынын корсетйп, s10-lLbI табыцдар:

       1) а =5п+З;                               2

256.   Жалпы »aweciHi1i формуласымен берћген геометриялык прогрессия болатынын корсетћ1, 'о-ды табьщдар:

з

                                                     2)bn =

257.   1) 100-ге №fTiHI'i барлык натурал сандардыц; 2) 16-дан 160-ка дейћтй барлык натурал сандардыц косындысын табыцдар.

в

258.1) 2+4+6+...+2п; 2) 1+3+5+...+(2n—1) косындысын табьщдар.

259.   Егер Щ —2, d=2 болса, онда {an} арифметикалык прогрессиясыньщ 20-муше(йнен бастап 25-муше(јне дећнй муше.лф1бц косындысын табьщдар.

260.   1) 200-ден аспайтын, З-ке есејйк натурал сандардыц; 2) 250-ден аспайтын, 9-га есе.тйк натурал сандардьщ косындысын табыцдар.

261.   Геометриялык прогрессияньщ алгашкы 8 MYIIIeciHi}l косындысы

85

— 64-ке, ал eceJIiTi q=— —-ге тец. Оныц 6ipiHIIIi мушесйн табыцдар.

262.   Егер геометрияльщ прогрессия упйн жене S3=1 З болса, 'I'i табьщдар.

263.   Егер арифметикалык прогрессия уп-йн — 28, S6=58 болса, S16ны табьщдар.

264.   Егер арифметикальщ прогрессия упйна6+а9+а1 +45=20 тецдйј орындалатын болса, куо-ны табьщдар.

265.   1) 1, з, 3²,         2) 2, 2², 2³

1

4) 1, х^а, х^и, ...; 6) 1, —r³, ...; геометриялык прогрессияларыньщ п мушес4}йц косындысын табыцдар.

266.   1) а =зп+1; 2) а =п+4; 3) а 4) Ь -0,2-53 5) Ь 6) Ь формулаларымен берћген Ti36ek'I'i1( бес

КОСЫНДЫСЫН аныктацдар.

с

267.   Арифметикалык прогрессия курайтын уш санныц косындысы 15-ке тец. Егер осы сандарга сайкес 1, 4 жене 19 сандарын коссак, онда геометрия.льщ прогрессияньщ алгашкы уш Mymeci шыгады. Осы уш санды табьщдар.

268.   Айырмасы нолден езгеше арифметикальщ прогрессияньщ ekiHIIIi, 6ipiHILIi жене упйнпй мушелејј осы тортћшен алганда геометриялык прогрессияньщ алгапщы уш мушесћ берејј. Геометрияльщ прогрессияныц ece.rriI'iH табьщдар.

269.   х; у; г сандары геометрияльщ прогрессия, ал х; 2у; Зг сандары арифметикальщ прогрессия курайды. Геометрияльщ прогрессияныц 1 -ден озгеше еселТн табыцдар.

270.   муше(й а-га, ал eceJIiI'i (1-ге тец геометрияльщ прогрессияныц п мушесћйц квадраттарыньщ косындысын аньщтацдар. 271. Геометрияльщ прогрессияньщ алгапщы п муше(йгбц ke6eiiTiHJLiciH ат жене а -мушелејј аркылы ернектендер.

56

272.{un} геометриялык прогрессиясы упйн ит + и5=51 жене + ив—102 тендйктегй орындалады. n-HiH кандай мэтйнде S —3069 болады?

273.

дар.

274.   Егер {ап} арифметикалык прогрессиясы          2ат болса, онда Sn—Sk тендйй орындалатынын долелдендер. sn+k

275.   Cyiiip бурышка 6ip-6ipiH сырттай жанайтын бфнеше шецбер ћптей сызылган. Шенберлердбн радиустары геометрияльгк прогрессия курайтынын далелдендер.

276.   а    Ti36eI'iHi}i алгашкы п rvrweciHiH косындысын табьщдар.

КАЙТА.ЛАУГА АРНАЛГАН ЭКАТГЫГУЛАР

277.   Ti36ek'I'i}i жалпы мушесйн жазындар:

1  2 з 4 5

1) 1; 4; 9; 25; 36•

9-43 9+445

278.                          +             орней1йц мегй буйн сан болатьшьш корсейндер.

279.                          х^а— х— 2=0 тецдеф график'йк тасћмен шепйцдер.

Еже.лб замандардан бастап адамзат арифметикалык жене геометриялык прогрессиялардыц зацдылыктарын колдана б№тген. Моселен, бКзхЙц заманымызга ежелй вавилондыктардьщ сына жазу (клинопись) kec'IPJIepiHJ(e, ежелй мысырлыктар мен гректердђц папирустарында арифметикалык жене геометрияльщ прогрессияларра кептеген мысалдар кездеседй. Ежелй грек галымдары прогрессиялардыц кейбф касиетчфн жене олардьщ косындысьш таба б)п-ен. Архимед (б. з. б. Ш р.) фигуралардын аудандары мен денелердйц келемдфн есептеуде сан Ti36eT'iHiH бђзнеше косындысын таба 6iJIIPH. Маселен, ол

1²+2²+3²+...+п²= корытып шыгарган. Ежелй замандардан геометриялык прогрессия ece.11iI'i 1-ден улкен болранда 1) ете экылдам каркынмен oceTiHJLiTi жекйнде мынадай аныз сакталган. Мэселен, ежелй унјј ПТГШаСЫ Шерам шахмат ойынын ойлап тапкан онертапкышты (оньщ аты Сета) марапатгау максатьшда оран калаганын алуды усынады. Сонда Сета шахмат тактасындагы 64 шар57