Районная научно - практическая конференция учащихся и педагогов

 

 

 

 

Предмет    «математика»

Номинация    «реферат проблемно – поискового характера»

 

 

Симметрия в жизни

 

 

 

 

 

 

 

 

 

Автор: Переплётов Алексей

учащийся 7 класса

МОБУ «Рыбкинская средняя общеобразовательная школа»

Научный руководитель: Окшина Л.А. (учитель математики)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

с. Рыбкино

Оглавление

Введение. 3

Раздел I. «Что такое симметрия». 4

Глава 1. Симметрия. 4

Глава 2. История симметрии. 5

Глава 3. Учёные, которые изучали симметрию.. 6

Раздел II.  Симметрия в предметах. 7

Глава 1. Симметрия в математике. 7

Глава 2. Симметрия в архитектуре. 9

Глава 3. Симметрия в биологии. 11

Глава 4. Симметрия в литературе. 14

Заключение. 16

Приложения. 17

Литература. 20

 

 

Введение.

    Актуальность.

      "Легко отыскать примеры прекрасного, но так трудно объяснить, почему они прекрасны".

Платон.

«Глядя на мир, нельзя не удивляться»

Козьма Прутков

«Красота тесно связана с симметрией»

Г.Вейль 

 

Понятие «симметрия» идёт из истоков человеческого понятия. Люди всегда пытались объяснить, почему одни вещи их привлекают, а другие отталкивают. Попытки понять это предпринимались с древнейших времён: математические законы Пифагора в музыке, система пропорций в скульптуре и архитектуре, геометрические законы в живописи.

Гуляя по лесу, по селу мне захотелось понять, почему цветы, насекомые завораживают, а дома в селе выглядят скучно и обыденно.

 

    Цель:

увидеть и понять тонкую нить, которая соединяет геометрию с красотой в жизни.

     Задачи:

1.   раскрытие особенностей видов симметрии;

2.   показ  всей привлекательности математики как науки и её взаимосвязь с природой в целом.

3.   сбор материала по теме реферата и его обработка;

4.   обобщение обработанного материала;

5.   выводы о проделанной работе;

6.   оформление обобщенного материала. 

 

 

Раздел I. «Что такое симметрия»

Глава 1. Симметрия.

Понятие симметрии встречается как во многих областях человеческой жизни, культуры и искусства, так и в сфере научных знаний. Но что такое симметрия? В переводе с древнегреческого языка это – соразмерность, неизменность, соответствие. Говоря о симметрии, мы часто имеем в виду пропорциональность, упорядоченность, гармоничную красоту в расположении элементов некоей группы или составляющих какого-то предмета.

В математике симметрию и ее свойства описывает теория групп. Симметрией в геометрии является способность фигур к отображению, при сохранении свойств и формы. В широком смысле фигура F обладает симметрией, если существует линейное преобразование, которое переводит эту фигуру в саму себя. В более узком смысле симметрией в математике называется зеркальное отражение относительно прямой с на плоскости или относительно плоскости с в пространстве.

Значение слова «Симметрия»

 по Ефремовой:

Симметрия - соразмерное, пропорциональное расположение частей чего-л. по отношению к центру, середине.

по Ожегову:

Симметрия - соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости

в Энциклопедическом словаре:

Симметрия - (от греч. symmetria - соразмерность) - в широком смысле -инвариантность (неизменность) структуры, свойств, формы материального объекта относительно его преобразований (т. е. изменений ряда физических условий). Симметрия лежит в основе законов сохранения.

по словарю Ушакова:

Симметрии, мн. нет, ж. (греч. symmetria). Пропорциональность, соразмерность в расположении частей целого в пространстве, полное соответствие (по расположению, величине) одной половины целого другой половине. Симметрия в планировке зданий на площади. Соблюдать симметрию.

по словарю Даля:

Симметрия ж. греч, соразмер, соразмерность, равно (или разно)подобие, равномерие, равнообразие, соответствие, сходность; одинаковость, либо соразмерное подобие расположенья частей целого, двух половин; сообразие, сообразность; противоравенство, противоподобие. Симметрическое расположенье дома, фасада, равнообразное на обе половины. Полная симметрия докучает, а изящное разнообразие красит и тешит вкус.

 

Глава 2. История симметрии

 

Представители первой научной школы в истории человечества, последователи Пифагора Самосского, пытались связать симметрию с числом. Каждой вещи, учили пифагорейцы, соответствует определенное отношение чисел, которое они называли логосом. Пифагорейцы предпочитали вместо слова «симметрии» пользоваться словом «гармония». Широко используя идею гармонии и симметрии, ученые древности любили обращаться не только к сферическим формам, но и к правильным многогранникам. У правильных многогранников грани – правильные многоугольники одного вида, а углы между гранями равны. Древние греки установили, что существует всего пять правильных выпуклых многогранников, название которых связаны с числом граней, - тетраэдр, октаэдр, икосаэдр, куб, додекаэдр. Все правильные многогранники обладают зеркальной симметрией.

Познавательную силу симметрии оценили философы Древней Греции, используя ее в своих натурфилософских теориях. Так, например, Анаксимандр из Милета, живший в первой половине VI в. до н. э., использовал симметрию в своей космологической теории, где в центре мира поместил Землю — главное, по его мнению, тело мира. Она должна была иметь совершенную, симметричную форму, форму цилиндра. Земля расположена точно в центре, и здесь симметрия имеет смысл равновесия.

Весы известны человеку с III в. до н. э. В состоянии равновесия массы грузов на разных концах коромысла одинаковы — положение коромысла симметрично относительно центра тяжести. Симметрия — это не только равновесие, но и покой: стоит добавить на одну из чашек весов дополнительный груз, как они придут в движение. Нарушено равновесие, исчезла симметрия — появилось движение.

Гармония (симметрия) состоит из противоположностей. В пространственной симметрии противоположности явно видны. Например, правая и левая кисти рук человека.

И Леонардо да Винчи не обошел своим вниманием симметрию. Он рассмотрел равновесие шара, имеющего опору в центре тяжести: две симметричные половины шара уравновешивают друг друга и шар не падает. Как художник он главное внимание уделял изучению законов перспективы и пропорций, с помощью которых выявляются художественные достоинства произведений искусства.

В науку симметрия вошла в 30-х гг. XIX в. в связи с открытием Гесселем 32 кристаллографических классов и появлением теории групп как области чистой математики. Кристаллы наделены наибольшей величиной симметрии из всех реальных объектов. Симметричной в кристаллографии считается фигура, которая делится без остатка на равные и одинаково расположенные части.

 

Глава 3. Учёные, которые изучали симметрию

 

Как говорил академик А.В. Шубников, посвятивший изучению симметрии всю свою долгую жизнь: «Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло её в рисунке и в предметах быта. Надо полагать, что применение симметрии в первобытном производстве определялось не только эстетическими мотивами, но в известной мере и уверенностью человека в большей пригодности для практики правильных форм».

С древних времен люди стремились найти (возможно, это было заблуждением?) те совершенные формы, идеальные движения и небесные гармонии, которые лежат в глубине беспорядочных и бесстрастных явлений окружающего мира. Пифагор, стремившийся упорядочить физические явления на основе гармоничных соотношений между целыми числами, пытался также объяснить движения планет, помещая последние на сферы, совершающие равномерные круговые движения; эту тему развивали потом Платон и многие астрономы вплоть до Кеплера. Сейчас круговые движения небесных сфер уже не в моде, однако, те виды симметрии, которые пришли на смену этим движениям, еще более привлекательны.

Именно благодаря исследованиям Пифагора мы знаем, что такое симметрия.

Но были и другие учёные, которые делали научные открытия именно на основе симметрии. Например: теорема Эйлера показывает, что  при наличии двух пересекающихся осей симметрии, через точку их пересечения проходит ось симметрии равнодействующая первым двум.

 

Раздел II.  Симметрия в предметах

 

Глава 1. Симметрия в математике

 

1. Центральная симметрия

Центра́льной симметри́ей относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. 

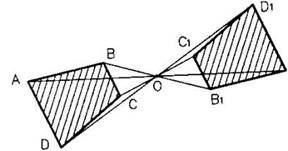          Понятие центральной симметрии следующее: «Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры». Поэтому говорят, что фигура обладает центральной симметрией.

Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма – точка пересечения его диагоналей. Любая прямая также обладает центральной симметрией. Однако, в отличие от окружности и параллелограмма, которые имеют только один центр симметрии, у прямой их бесконечно много – любая точка прямой является её центром симметрии.

 

 

                               

 

 

 

 

     2. Осевая симметрия

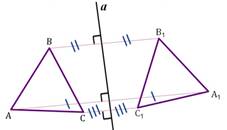    Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М₁ относительно оси а    

 Понятие осевой симметрии представлено следующим образом: «Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая a называется осью симметрии фигуры». Тогда говорят, что фигура обладает осевой симметрией.

Примеры фигур, обладающих осевой симметрией: равнобедренный (но не равносторонний) треугольник имеет одну ось симметрии, а равносторонний треугольник— три оси симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют по две оси симметрии, а квадрат— четыре оси симметрии. У окружности их бесконечно много — любая прямая, проходящая через её центр, является осью симметрии.

 

 

 

   

 

 

 

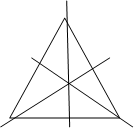
 3. Зеркальная симметрия

          Зеркальная симметрия хорошо знакома каждому человеку из повседневного наблюдения. Как показывает само название, зеркальная симметрия связывает любой предмет и его отражение в плоском зеркале. Говорят, что одна фигура (или тело) зеркально симметрично другой, если вместе они образуют зеркально симметричную фигуру (или тело).

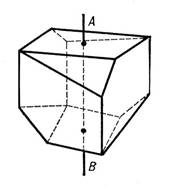
4. Поворотная симметрия

· Знакомое понятие  параллельного переноса используются при определении так называемой переносной симметрии. Этот вид симметрии состоит в том, что части целой формы организованы таким образом, что каждая следующая повторяет предыдущую и отстоит от нее на определенный интервал в определенном направлении. Этот интервал называют шагом симметрии.

 

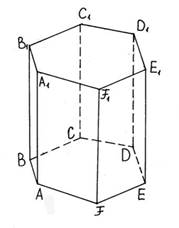
Многоугольник АВСDEF переходит

 в многоугольник А₁ В₁С₁D₁E₁F₁ 

с шагом симметрии F F_1.

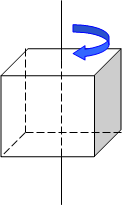Понятие поворота  даёт представление о поворотной симметрии. В этом случае переход частей в новое положение и образование исходной фигуры происходит при повороте этой фигуры на определенный угол  вокруг точки, которая обычно называется центром поворота. Отсюда и приведенное выше названия указанного вида симметрии. Поворот куба на 90 градусов относительно оси симметрии  переводит его в самого себя.

 

Глава 2. Симметрия в архитектуре

 

         Человеческое творчество во всех своих проявлениях тяготеет к  симметрии. На этот счёт хорошо высказался известный французский архитектор Ле Корбюзье, в своей книге «Архитектура XX века» он писал: «Человеку необходим порядок: без него все его действия теряют согласованность, логическую взаимность. Чем совершеннее порядок, тем спокойнее и увереннее чувствует себя человек. Он делает умозрительные построения, основываясь на порядок, который продиктован ему потребностями его психики, это творческий процесс. Творчество есть акт упорядочения».

    Нагляднее всего видна симметрия в архитектуре.

Осевая симметрия применена в красивых воротах

 

    Классические здания XIX – начала XX века в основном выдержаны в рамках зеркальной симметрии.  (Здания Адмиралтейства и Кунсткамеры в С-Петербурге) 

 

 

   Исключения составляют церкви. Часто причудливая композиция состоит из нескольких храмов, каждый из которых обладает различными видами симметрии. Маковки соборов обладают центральной симметрией. Каждое из строений тоже симметрично, но плоскость симметрии расположена по-разному. Соединенные вместе, симметричные архитектурные детали соборов «кружатся» в своём асимметричном «танце», создавая впечатление радости и праздника.

    Примером удивительного сочетания симметрии и асимметрии является Покровский собор в г. Оренбурге.

 

Центральной симметрией обладает Дом Памяти

 

Изредка в архитектуре встречается винтовая симметрия.

Винтовая (спиральная) симметрия — это симметрия объекта относительно группы преобразований, являющихся композицией преобразования поворота объекта вокруг оси и переноса его вдоль этой оси.

Спиральная симметрия в искусстве встречается в чистом виде мало, в основном она присутствует в узорах, изредка – в архитектуре (винтовые лестницы, витые колонны), графическом дизайне. Её изобразительная особенность состоит в поступательном движении точки, линии, плоскости, формы с постоянной угловой скоростью вдоль неподвижной осевой линии. Этот тип симметрии с успехом может применяться в разработке фирменных знаков.

 

 

 

Глава 3. Симметрия в биологии

 

       Законы природы являются симметричными, но при ближайшем их рассмотрении, в каждом из них можно найти хоть небольшой изъян. Оказывается, что природа не терпит точной симметрии. Природа почти, но не абсолютно, симметрична. Примером этому являются догадки Пифагора, который считал, что орбиты, по которым движутся планеты, являются совершенными окружностями, на самом же деле это не так.   

Объекты и явления живой природы обладают  симметрией. Она не только радует глаз и вдохновляет поэтов всех времен и народов,  а позволяет живым организмам лучше приспособиться к среде обитания и просто выжить.

В живой природе огромное большинство живых организмов обнаруживает различные виды симметрии (формы, подобия, относительного расположения). Причем организмы разного анатомического строения могут иметь один и тот же тип внешней симметрии.

 

Симметрия растений (Приложение. Таблица 1)

          Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля.

Среди цветов наблюдаются поворотные симметрии разных порядков. Многие цветы обладают характерным свойством: цветок можно повернуть так, что каждый лепесток займёт положение соседнего, цветок же совместится с самим собой. Такой цветок обладает осью симметрии. Минимальный угол, на который нужно повернуть цветок вокруг оси симметрии, чтобы он совместился с самим собой, называется элементарным углом поворота оси. Этот угол для различных цветов не одинаков. Для ириса он равен 120⁰, для колокольчика – 72⁰, для нарцисса – 60⁰ .

          

 

 

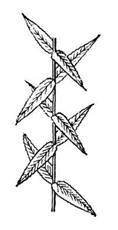     В пространстве существуют тела, обладающие винтовой симметрией, т. е. совмещающиеся со своим первоначальным положением после поворота на угол вокруг оси, дополненного сдвигом вдоль той же оси.

     Винтовая симметрия наблюдается в расположении листьев на стеблях большинства растений. Располагаясь винтом по стеблю, листья как бы раскидываются во все стороны и не заслоняют друг друга от света, крайне необходимого для жизни растений. Это интересное ботаническое явление носит название филлотаксиса, что буквально означает строение листа. Другим проявлением филлотаксиса оказывается устройство соцветия подсолнечника или чешуи еловой шишки, в которой чешуйки располагаются в виде спиралей и винтовых линий. Такое расположение особенно четко видно у ананаса, имеющего более или менее шестиугольные ячейки, которые образуют ряды, идущие в различных направлениях.

  

   

 Симметрия животных (Приложение. Таблица 2)

          Внимательное наблюдение обнаруживает, что основу красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды – от простейших до самых сложных. Симметрия в строение животных – почти общее явление, хотя почти всегда встречаются исключения из общего правила.

     Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. Строение тела многих многоклеточных организмов отражает определённые формы симметрии.

 

Осевой симметрией обладает хвост павлина, крылья бабочки

 

 

 

Также в животном мире встречается винтовая симметрия

 

 

 

 

Глава 4. Симметрия в литературе

 

Под симметрией в искусстве подразумевается гармоничная композиция. Поэзия отличается от прозы более высоким и гармоничным уровнем организации художественной формы. Четкий ритм, закономерное чередование ударных и безударных слогов, упорядоченная размерность стихотворений, их эмоциональная насыщенность.

Осевая симметрия может встретиться в стихотворениях. Например:

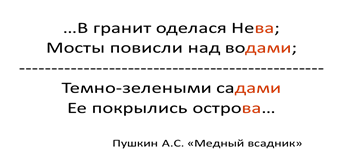
Все мы читали сказку А.Толстого «Золотой ключик» и смотрели фильм или мультфильм. Там Мальвина диктовала Буратино всем известную «волшебную» фразу: «А роза упала на лапу Азора». Она читается и слева направо и справа налево одинаково. Автором этой фразы считается русский поэт XIX века А.А.Фет.

Это и есть так называемый «палиндром». Палиндромом (от гр. Palindromos – бегущий обратно) можно назвать некоторый объект, имеющий линейную или циклическую форму организации, в которой задана симметрия составляющих от начала к концу и от конца к началу

В зависимости от числа и вариации места словоразделов, а также меры совпадения прямого и обратного чтения палиндромы классифицируются по степени сложности и точности. Прямой текст палиндрома, читающийся в соответствии с нормальным направлением чтения в данной письменности (во всех видах кириллической и латинской письменности – слева направо), называется прямоходом, обратный – ракоходом или реверсом (справа налево). Классический пример палиндрома:

Я – арка края (В.Брюсов).

Существует несколько разновидностей палиндромов: буквопалиндромы – читаются туда и обратно точно по буквам; словодромы (читаются уже не по буквам, а по словам и в ту, и в другую сторону); слогодромы и др. Также распространены и оборотни, читаемые справа налево иначе, чем слева направо. Причем, при их обратном прочтении текст, обычно имеет противоположный, замаскированный смысл. Например, на Ритке снег (С.Федин). А обратно получается нечто оригинальное: Генсек - тиран.

Примеры некоторых палиндромов:

 

А Вера – рева

А к порту тропка

Аргентина манит негра

Бел хлеб

Вор в лесу сел в ров

Голод долог

Диван нежен на вид

Ешь немытого ты меньше!

Ишаку казак сено нес, казаку – каши

Кит на море – романтик

Колька нес сена клок

Конус и рисунок

Лепил и пел

Леша на полке клопа нашел

Мокнет Оксана с котенком

Мороз узором

Тропа налево повела, на порт

Туши рано фонари, шут!

 

 

 

     Заключение

 

  С симметрией мы встречаемся везде: в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии. Существует множество видов симметрии как в растительном, так и в животном мире, но при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира.

  1)    Симметрией обладают объекты архитектуры  и явления живой природы.

2)    Существует несколько основных типов симметрии, которые могут сочетаться друг с другом, так как живой мир многообразен и неповторим.

3)    В живой природе огромное большинство живых организмов обнаруживает  сочетание различных видов симметрии.

Вид симметрии	Предмет
Центральная симметрия	Математика, архитектура, биология, литература
Осевая симметрия	Математика, архитектура, биология, литература
Зеркальная симметрия	Математика, архитектура
Винтовая симметрия	Математика, архитектура, биология
Поворотная симметрия	Математика, архитектура

 

 Помимо симметрии встречается и асимметрия.

Симметрия и асимметрия - это два важных компонента, которые объединяют красоту, совершенство, идеал. Симметрия противостоит хаосу, беспорядку. Она присутствует в нашей жизни буквально во всём, но мы настолько к ней привыкли, что не замечаем этого. Но как бы мы к ней не относились, она есть в нашей жизни, добавляя в неё мир, спокойствие и состояние чего-то нечуждого глазу.

 Асимметрия наоборот вдыхает в мир необычные формы, замысловатые фигуры, но от этого мир становится только ярче и интересней.

Сведение красоты только к симметрии ограничивало  богатство её внутреннего содержания, лишало красоту жизни. Истинную красоту можно постичь только в  единстве противоположностей. Вот почему единство симметрии и асимметрии определяет сегодня внутреннее содержание прекрасного в искусстве. Симметрия воспринимается нами как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность.

А вместе они являются основой прекрасного.

Про асимметрию будет моя следующая работа.

 

Приложения

Таблица 1

Геометрия	Описание симметрии	Примеры
Центральная симметрия (лучевая симметрия)	Целый веер или пучок пересекающихся плоскостей симметрии.	Цветы растений, Мутовчатое расположение листьев на стебле (хвощ).
Поворотная симметрия	Говорят, что объект обладает поворотной симметрией, если он совмещается сам с собой при повороте на угол 20/n, где n может равняться 2, 3, 4 и т.д. до бесконечности. Ось симметрии называется ось осью n-го порядка. Цветок можно повернуть так, что каждый лепесток займет положение соседнего, цветок совместится с самим собой.	Цветки колокольчика, вишни,  груши, незабудки, герани, рябины, боярышника и др.
Винтовая симметрия.	Листья на стебле расположены не по прямой, а окружают ветку по спирали. Сумма всех предыдущих шагов спирали, начиная с вершины, равна величине последующего шага	Расположении листьев на стеблях большинства растений.
Переносная симметрия	О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние а либо расстояние, кратное этой величине, она совмещается сама с собой.	Шишки хвойных растений.
Зеркальная симметрия, осевая симметрия.	Листок как бы склеен из двух более или менее одинаковых половинок. Одна из этих половинок расположена зеркально относительно другой, совсем так, как располагаются друг относительно друга отражение какого-либо предмета в зеркале и сам предмет. Плоскость, разделяющая листок на две зеркально равные части называется «плоскостью симметрии».	Листья растений

 

Таблица 2

Тип симметрии	Описание симметрии	Примеры
Вращательная (радиальная).	Характеризуется тем, что одинаковые части тела и органы располагаются по радиусам от срединной продольной оси животного. Тело с радиальной симметрией может быть разделено на равные части несколькими плоскостями, проходящими через эту ось.	Радиальная симметрия тела свойственна преимущественно животным, ведущим сидячий или малоподвижный образ жизни или пассивно плавающим в воде. Примером подобных животных могут служить гидры, медузы, морские звезды.
Вращательно-поступательная.	Симметрия характерна тем, что при повороте на определённый угол часть тела немного проступает вперед и её размеры   каждый следующий логарифмически увеличивает на определённую величину. Таким образом, происходит совмещение актов вращения и поступательного движения.	Спиральные камерные раковины фораминифер,  также спиральные  раковины некоторых моллюсков.
Двусторонняя симметрия (билатеральная, поступательная).	Тело животного отличается тем, что только одна плоскость может разделить его на две равные половины. У двустороннесимметричных животных можно различить левую и правую половины, передний и задний концы тела.	Данная симметрия присуща преимущественно животным, способным к самостоятельным передвижениям. Как правило, она бывает неполной, относительной. Обычно организм двустороннесимметричного животного снаружи более или менее правильно симметричен (левая и правая половина его почти одинаковы), но в расположении многих внутренних органов наблюдается явная асимметрия. Так, например, у человека сердце лежит в левой части грудной клетки, у птиц яичник расположен в левой части таза и т. д. Примеры: человек, бабочка, рак и др.
Метамерия (разновидность поступательной симметрии).	Части тела расположены не зеркально друг против друга, а последовательно друг за другом вдоль главной оси тела.	Ярко выражена у кольчатых червей.

 

Литература

 

1.   А.И. Азевич «Двадцать уроков гармонии» библиотека журнала «Математика в школе», выпуск 7. Москва «Школа-Пресс», 1998 год

2.   «Большая энциклопедия Кирилла и Мефодия. 2007г.»

3.   «Большая энциклопедия школьника»

4.   А.В. Волошинов «Математика и искусство», Москва, «Просвещение», 1992 год.

5.   Тарасов Л. «Этот удивительно симметричный мир: пособие для учащихся», Москва, «Просвещение», 1982 год.

6.   Wikipedia.ru

7.   Geometry-and-art.ru

8.   Spravochnik.ru

9.   Infourok.ru

 

 

 

Скачано с www.znanio.ru