Система скремблер дескремблер со сменным секретным ключом.docx

Система скремблер/дескремблер со сменным секретным ключом.

Сигнал речи, оцифрованный, например, δ-модулятором (рис. 2 и 3, раздел 2.2.), можно рассматривать как непрерывный поток бит.

Аппаратно и программно простыми и дешёвыми способами являются:

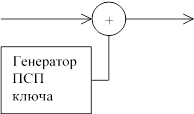
1)      Метод гаммирования (рис.1) с помощью сумматоров по модулю два и двух одинаковых на приёмной и передающей стороне генераторов ПСП в качестве ключей шифрования и дешифрования. Поток бит ключа называют гаммой.

2)      Устройства скремблер/дескремблер на базе регистра сдвига с обратными связями на сумматорах па модулю два, рассмотренных в разделах 2.4. и 2.5.

Кодек (устройство кодирования/декодирования) оцифрованного сигнала речи на базе схемы с рис.1 требует, чтобы в реальном времени начало кодирования и начало декодирования   строго   совпадали   по   фазе,   с   точностью   до   бита   после   каждой

«микропаузы» речи. Сдвиг ключа K относительно шифрограммы C_i всего на один бит приводит к полному нарушению процесса декодирования на приёмной стороне, так как генераторы ПСП приёма и передачи не синхронизированы. Эту задачу решают с помощью сложного и дорогого, как программного, так и аппаратного обеспечения. Однако кодек работающий по  схеме  с  рис.1 имеет несомненное достоинство: наличие секретного ключа.

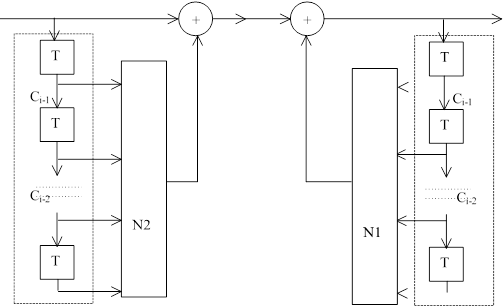
Кодек на базе регистра сдвига прост и дёшев и обладает свойством самосинхронизации, заключающемся в том, что через несколько тактов (не больше числа разрядов регистра сдвига) состояния регистров шифратора и дешифратора выходят на режим совпадения, после чего устанавливается нормальная работа кодека, когда y_i = x_i.

Однако различных схем обратных связей регистра сдвига не так много.  Поэтому, перехватив шифрограмму C_i на линии связи, можно вскрыть конфигурацию скремблера.

Количество различных ключей, которые можно записать в ПЗУ с p-разрядными адресами одноразрядных ячеек памяти, равно

M = 2 2p

Например, для p = 8 получим: длина ключа M = 2²⁵⁶ = 1.15*10⁷⁷.

В разделе 2.3 доказано, что для скремблера/дескремблера с ключом на ПЗУ выполняется равенство y_i = x_i.

Докажем теперь, что выполняется также и свойство самосинхронизации. Возьмём возможный алгоритм функционирования модели нашей системы.

1    ввод N1

2    ввод N2

3    ввод x

4  K1 := f(N1)

5  K2 := f(N2)

6    C := x XOR K1

7    y := C XOR K2

8    печать x, N1, C, N2, y

9    N1 := сдвиг RG1

10    N2 := сдвиг RG2

11    GO TO 3

Система возбуждается тактовыми импульсами, генератор которых на передающей стороне и устройство выделения их из полученного сигнала на приёмной стороне на рисунке не показаны.

Система обладает свойством самосинхронизации, состоящем в том, что через некоторое количество тактов состояние регистров становится одинаковым:

N1_i = N2_i = N_i.

Для последующих тактов наступает равенство y_i = x_i для любых ключей, одинаковых для приёмника и передатчика:

f(N1_i) = f(N2_i) (1)

Докажем это. Действительно из (1) вытекает, что начнут совпадать и биты ключей: K1_i = K2_i = K_i.

Согласно 6-7 строк алгоритма будем иметь:

y_i = C_i ⊕ K_i = x_i ⊕ K_i ⊕ K_i.

Но так как K_i ⊕ K_i = 0, то то получаем при самосинхронизации y_i = x_i.

Количество тактов необходимых для выхода на самосинхронизацию определяется разницей в начальных состояниях регистров и количеством разрядов в них.

Пусть RG имеют p разрядов. Рассмотрим множество подгрупп младших бит двоичного числа N состояния регистра, то есть следующие подгруппы младших бит:

(a₀), (a₁, a₀), (a₂, a₁, a₀), (a₃, a₂, a₁, a₀) и так далее, где a∈{0, 1}.

Обозначим биты регистра RG1 символами ‘a’, биты регистра RG2 - символами ‘b’.

Так как при операции сдвига в регистрах в их младший бит записывается одинаковая информация C_i ∈{0, 1}, то возможны следующие случаи:

1)      Если m младших бит, как начальных, так и очередных состояний регистров, совпадают:

am-1am-2…a1a0 = bm-1bm-2…b1b0,

то какая бы информация C_i (либо 0, либо 1) ни записывалась бы в младший разряд регистров, после этого такта будут совпадать уже m+1 младших разрядов.

Например:

N1 = …x101,

N1 = …x101, где х∈{0, 1} – безразлично какой бит; После сдвига при C_i = 1 получим:

N1 = …x1011,

N1 = …x1011 – совпадают четыре младших бита, После сдвига при C_i = 1:

N1 = …x1010,

N1 = …x1010 – совпадают четыре младших бита.

Следовательно через (p – m) начнётся полное совпадение состояний регистров и в каждом последующем такте будет N1 = N2, независимо от очередного значения C_i.

2)      Если в начальных состояниях регистров нет совпадений для каждой подгруппы младших бит, то есть m = 0, то самосинхронизация устанавливается через p тактов. Например, пусть p = 4, и пусть в RG1 находится число N1, а в  RG2  -  число  N2.тогда при очередных сдвигах с произвольным C_i получим:

Совпадения начинаются на 4-ом такте. Здесь в исходном состоянии N2 есть инверсия N1: m = 0.

Совпадения начинаются на 4-ом такте. Здесь все подгруппы младших бит не совпадают: m

= 0.

Итак, при самых неблагоприятных начальных состояниях регистров самосинхронизация наступает через p тактов.

Как видно из вышеизложенного, выход на самосинхронизацию не зависит от ключевой последовательности нулей и единиц, записанных в ПЗУ, если таблицы f(N1) и f(N2) содержимого обеих ПЗУ одинаковы.