Системный контроль и учет знаний учащихся .

           Система контроля и оценки позволяет установить персональную ответственность учителя и школы в целом за качество процесса обучения. Результат деятельности учительского коллектива определяется прежде всего, по глубине прочности и систематизации знаний учащихся, уровню их воспитанности и развития.

          Проверка и оценка достижений младших школьников является весьма существенной составляющей процесса обучения одной из важных задач педагогической деятельности учителя. Этот компонент, наряду с другими компонентами, учебно-воспитательного процесса должен соответствовать современным требованиям общества, педагогической и методической наукам, основным приоритетам и целям образования в первом звене школы.

          Система контроля и учета знаний не может ограничиваться целью – проверкой усвоения знаний и выработки умений и навыков по конкретному учебному предмету. Она ставит более важную социальную задачу: развить у школьников умение проверять и контролировать себя, критически  оценивать свою деятельность, находить ошибки и пути их устранения.

          В настоящее время интенсивно развиваются школьные педагогические технологии, и появилось много направлений. Я придерживаюсь различных видов контроля и учета знаний. Цель этой технологии заключается в проверке знаний и умений не только на этапе итогового контроля, но и текущего. Эта технология развивает интерес к предмету, позволяет провести устный или письменный опрос учащихся всего класса. Дети правильно формулируют ответы на вопросы, развивается логическое мышление, улучшает подготовку к обязательной контрольной работе.

          Для формирования инициативности позитивной «Я – концепции» желательно делегировать учащимся некоторые полномочия учителя.  Очень хорошо зарекомендовала себя на практике инсценировка «ученик – учитель». Если у учителя есть система в опросе и закрепление знаний, то запуск этой технологии не составляет труда. Учитель на уроке как «капитан на мостике», только наблюдает и направляет. Достижение целей обучения развития и воспитания будет более успешным. При такой педагогической технологии обучения развивается мотивация учащихся за счет позиции ученика с пассивной на активную, у детей снимается уровень тревожности, страх перед контрольными работами. Они ориентируются на самостоятельность, активность, самоконтроль, формулируются целевые установки, ликвидируются пробелы в знаниях.

         Проблема счета остается актуальной для современного уровня развития науки. Не смотря на то, что во многих семьях появляются калькуляторы, компьютеры, учащиеся должны хорошо научиться читать, считать, научиться видеть силу цифр. Вычислительные навыки являются стратегическими при обучении.

Эта система отвечает современным запросам, открывает возможности постоянного совершенства, приносит лучшие,  результаты по сравнению с массовой практикой. Что здесь нового? То, что дети сами задают вопросы и сами отвечают на них («Домино»). Идет постепенное накопление теоретического материала и осмысленное применение на практике.  То, что после каждого нового материала учитель видит, как поняли дети новую тему. Кто не понял, сразу  этот пробел решается, и ребенок переступает на другую ступеньку знаний. При такой педагогической деятельности происходит увеличение объема информации.   

Методика позволяет целесообразно и грамотно доводить формируемую познавательную деятельность до оптимальных результатов (осознанность, прочность, автоматизм вычисления). Тот ребенок, который пропустил по болезни несколько дней, быстро успевает усвоить пропущенный материал и он не остается без внимания учителя. Учитель сразу дает ему карточки по пропущенной теме, может индивидуально объяснить, прикрепить «учителя-ученика». Какой фактор успешности в этой системе? Эффективно формируется у школьников положительное отношение к учебе, направленное на снятие страха. При такой системе в классе присутствует дух соревнования: а кто быстрее  решит карточки с заданием; у кого будет первый флажок; кто будет учителем?

            Актуальность и перспективность опыта заключается в том, что повышается качество знаний учащихся в классе, нацеленность на получение прочных знаний и умений в будущем. Хорошая творческая преемственность для других учителей. Необходимость создания данной методики в том, что дети плохо воспринимают изложение нового материала, не могут самостоятельно сделать домашнее задание, т.к. плохая память, не развита речь, страх перед непонятным.

Основная идея методики – это сотрудничество педагога и школьника на основе взаимного уважения и доверия. Идея максимальной помощи ученику в познании и самоутверждении. В чем трудность методики? Все трудности были на ранней стадии ее возникновения. Большие временные затраты ушли на создание  «Домино», системных зачетных карточек, созданных по типу от «простого к сложному», ведение строго учета знаний учащихся. Учителю, желающему использовать мою методику, уже будет просто. Учитывая современную компьютерную технику, не составит большого труда и времени все это использовать в учебном процессе.

Основным принципом обучения является доступность, учет основных и индивидуальных возможностей, повышение уровня знаний.

Приемы обучения – это разъяснение, осмысление учебного материала, применение теории на практике. Одобрение, похвала, внушение – приемы воспитания.

Основными средствами обучения является учебник математики и русского языка, опоры малые и большие, карточки с заданием. «Домино» - карточки с теоретическим материалом.

Средством воспитания является выдвижение лидера в классе, воспитание коллективизма, взаимовыручки, переживание за конечный результат. Основной формой педагогической деятельности является урок, индивидуально-групповое занятие, группа продленного дня, викторина, неделя математики, неделя русского языка.

            При такой системе педагог использует сразу несколько целей: образовательные, воспитательные, развивающие, индивидуальные, фронтальные.

            Использование педагогического комплекса позволяет достичь хороших результатов. Если изобразить схематически, то получится такая педагогическая концепция.

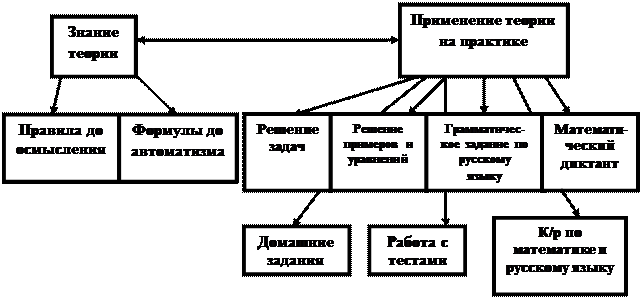
В настоящее время, когда в учебном процессе весьма редко применяются технические системы контроля и самоконтроля, необходимо шире и активнее использовать традиционные, индивидуальные раздаточные материалы и наглядные пособия в качестве средств обратной связи:    

Сигнальные карточки, знаки, сигнальные блокноты. Все эти простейшие средства обучения позволяют добиваться значительных положительных результатов.

            При организации итогового контроля необходимо ориентироваться, прежде всего, на основные требования программы, строя уроки так, чтобы на каждом из них проверялось усвоение пройденного материала. На уроках повторения важно организовать повседневную проверку и учет их усвоения каждым учеником класса. В этих целях могут использоваться такие приемы, как взаимная проверка знаний таблиц учащимися, арифметические диктанты. Важно также продолжать интенсивную тренировку в устных и письменных вычислениях,  решать задачи всех рассмотренных видов.    

Я поставила перед собой цель – ребенок должен хорошо знать, во-первых, теоретический материал, а во-вторых, применять его на практике. Были составлены  вопросы и ответы по русскому языку и по математике. Ребята сами задавали вопросы и сами на них отвечали. Учитель поощрял тех учащихся, которые отвечали на вопрос правила, не глядя в карточку, т.е. наизусть. В конце года все дети очень хорошо усвоили теоретический материал, уверенно отвечали на вопросы учителя, хорошо справлялись с тестами.

 «Домино» по математике позволяет ученикам запоминать и правильно применять на практике правила сложения, вычитания, решения задач и т.д. Каждая карточка «Домино» состоит из вопроса и ответа, который не соответствует вопросу. На первой карточке ответа нет. Это сделано специально, когда такая карточка попадает кому-то из детей, ученик знает, что он начинает игру, то есть первый задает вопрос. Остальные дети должны внимательно слушать и искать ответ в своих карточках. Тот, кто ответит на поставленный вопрос, задаст свой, сказав громко: «Вопрос»,  а потом только прочитает в карточке вопрос.

ИГРА «ДОМИНО»

(теоретический материал).

1. Как найти делитель, делимое

    и частное?

                   Вопрос           

2. Как найти уменьшаемое,                       Чтобы найти делитель, надо делимое разделить

    вычитаемое и разность?                        на частное.

                                                                     Чтобы найти делимое, надо частное умножить

                                                                     на делитель.

                                                                     Чтобы найти частное, надо делимое разделить

                                                                     на делитель.

                   Вопрос

3. Как найти первый и второй                 Чтобы найти уменьшаемое, надо к разности         

    множители?                                           прибавить вычитаемое.

                                                                    Чтобы найти вычитаемое, надо от уменьшаемого

                                                                    вычесть разность.

                                                                    Чтобы найти разность, надо от уменьшаемого                                                                                       вычесть вычитаемое.

  4. Как найти произведение?                    Чтобы найти первый множитель, надо                                                                                                     произведение разделить на второй  множитель.

                                                                      Чтобы найти второй множитель, надо

                                                                      произведение разделить на первый множитель.

  5. Как найти первое и второе                  Чтобы найти произведение, надо первый                                                                                      слагаемые?                                            множитель       умножить на второй множитель.

                                                                    От перестановки множителей произведение не                                                                                меняется.

 6. Как найти сумму чисел?                      Чтобы найти первое слагаемое, надо из суммы

                                                                     вычесть второе слагаемое.

                                                                     Чтобы найти второе слагаемое, надо из суммы

                                                                     вычесть первое слагаемое.

7. Когда сумма равна одному                   Чтобы найти сумму чисел, надо первое и второе

    из слагаемых?                                         слагаемые сложить. От перестановки слагаемых

                                                                     сумма не изменяется.

8. Когда разность равна нулю?                 Сумма равна одному из слагаемых, если другое

                                                                       слагаемое равно нулю.       

                                                                       Пример: 456 + 0 = 456

                                                                                       а + 0 = а

9. Как увеличить число в                           Разность равна нулю, если уменьшаемое

    несколько раз или увеличить                равно вычитаемому.

    на несколько единиц?                            Пример: 456 – 456 = 0

                                                                                       а – а = 0

10. Когда  произведение равно                  Увеличить число в несколько раз, значит

      нулю.                                                       умножить.

                                                                       Увеличить число на несколько единиц, значит

                                                                       прибавить.

11. Когда произведение равно                    Произведение равно нулю, если один из

      одному из множителей?                       множителей равен нулю.

                                                                       Пример: 456 × 0 = 0

                                                                                       а × 0 = 0   

12. Как уменьшить число на                       Произведение равно одному из множителей,

      несколько единиц или в                        если один из множителей равен 1.

      несколько раз?                                        Пример: 456 × 1 = 456

                                                                                        а × 1 = а              

13. Когда частное равно 1 и                       Уменьшить число на несколько единиц, значит

      нулю?                                                      вычесть.

                                                                       Уменьшить число в несколько раз, значит                                                                                            разделить.

14. Можно ли делить на нуль и                 Частное равно 1, если делимое равно делителю.

      когда делимое равно частному?           Пример: 125 : 125 = 1

                                                                                       а : а = 1

                                                                       Частное равно нулю, если делимое равно нулю.

                                                                       Пример: 0 : 8 = 0

                                                                                      0 : а = 0

15. Как найти цену, если                              На нуль делить нельзя:  а : 0 !

      известны количество и                           Делимое равно частному, если делитель равен 1.

      стоимость.                                                Пример:    75 : 1 = 75

                                                                                            а : 1 = а                                           

16. Как найти количество, если                  Чтобы найти цену, надо стоимость разделить на

      известны стоимость и цена?                 количество:                  Ц = Ст. : К.

17. Как найти стоимость, если                    Чтобы найти количество, надо стоимость                                                                   известны количество и цена?                разделить  на цену:     К = Ст : Ц

18. Из чего состоит класс                           Чтобы найти стоимость, надо цену умножить

      единиц?                                                  на количество:            Ст = Ц × К.

19. Из чего состоит класс                           Класс единиц состоит из единиц, десятков и

      тысяч?                                                     сотен.            

20. Назовите  единицы длины.                   Класс тысяч состоит из единиц тысяч, десятков

                                                                       тысяч, сотен тысяч.

21. Назовите единицы массы.                     Единицы длины:

                                                                        в 1 см = 10 мм

                                                                        в 1 дм = 10 см

                                                                        в 1 дм = 100 мм

                                                                        в 1 м = 10 дм

                                                                        в 1 м = 100 см

                                                                        в 1 м = 1000 мм

                                                                        в 1 км = 1000 м

22. Назовите единицы времени.                Единицы массы:

                                                                       в 1 кг = 1000 г

                                                                       в 1 т = 1000 кг

                                                                       в 1 ц = 100 кг

                                                                       в 1 т = 10 ц

23. Как  найти расстояние?                         Единицы времени:

                                                                       В 1 мин. = 60 с

                                                                       В 1 сут. = 24 ч

                                                                       В ч = 60 мин.

                                                                       В 1 неделе = 7 дней

                                                                       В 1 году = 12 месяцев

                                                                       В 1 месяце = 30,31,28,29 дней

                                                                       В 1 веке = 100 лет

                                                                       В 1 году = 365 или 366 дней

24. Как найти время?                                  Чтобы найти расстояние (S), надо скорость (V)

                                                                       умножить на время(t) :            S = V ×t

25. Как найти скорость?                             Чтобы найти время (t), надо расстояние (S)                                                                                           разделить на скорость (V) :     t = S : V

26. Что такое скорость?                              Чтобы найти скорость (V), надо расстояние (S)

                                                                       разделить на время (t) :           V = S : t

27. Как умножить однозначное                  Скорость – расстояние, пройденное за единицу

     число на многозначное,                         времени.     например 5 х 546 = ?  

28. Что такое отрезок?                                 Надо множители переставить местами, т.е.                                                                                           многозначное умножить на однозначное: 546 х 5.

                                                                       При перестановке множителей произведение не                                                                                  меняется .

29. Что такое треугольник?                        Отрезок – часть прямой, ограниченный с двух

                                                                        сторон.                                              

                                                                                                                          .В

  А.                                                          

30.Что такое четырехугольник?                  Треугольник – геометрическая фигура, в которой                                                                                три угла и три стороны.

31. Что такое прямоугольник?                   Четырехугольник – геометрическая фигура, у                                                                                       которой четыре угла и четыре стороны.

32. Что такое квадрат?                                 Прямоугольник – четырехугольник, у которого

                                                                       все углы прямые. Противоположные стороны

                                                                       прямоугольника равны.

33. Что такое периметр?                               Квадрат – прямоугольник, у которого все                                                                                              стороны равны.      

34. Что такое площадь?                                Периметр (Р) – сумма сторон какой-нибудь                                                                                          геометрической фигуры.

35. Как найти периметр прямо-                   Площадь (S) внутренняя часть какой-нибудь гео-

      угольника?                                               метрической фигуры.

36. Как найти сторону прямо-                      Периметр прямоугольника Р_{пр =} (а + в) × 2.

      угольника по известной                           Пример:      а = 3 см

      стороне и периметру?                                                   в = 4 см

                                                                                               Р_{пр.=  ?}

                                                                                                                              Р_пр=(а+в) × 2

                                                                                               Р_пр=14

37. Как найти периметр                               Сторона прямоугольника: а = Р_пр : 2 – в

      квадрата?                                                 Пример:        в = 6 см

                                                                                               Р_пр=16 см

                                                                                               а = ?

                                                                                               а= Р_пр  : 2 – а

                                                                                               а = 16 : 2 – 6

                                                                                               а = 2 см

38. Как найти сторону квадрата                  Периметр квадрата:  Р_кв = а× 4

      по известному периметру?                   Пример:        а = 7 см

                                                                                               Р_кв=?

                                                                                               Р_кв= а× 4

                                                                                               Р_кв=7 × 4

                                                                                               Р_кв= 28 см

39. Как найти площадь                                Стороны квадрата: а = Р_кв  : 4

      прямоугольника?                                   Пример:         Р_кв = 32 см    

                                                                                               а = ?

                                                                                               а = Р_кв  : 4

                                                                                               а = 32 : 4

                                                                                               а = 8 см

40. Как найти сторону                                 Площадь прямоугольника: S _пр =а × в                                                                 прямоугольника, если                            Пример:       а = 3 см

     известна площадь и сторона?                                        в = 4 см

                                                                                               S _пр=?

                                                                                               S _пр=а × в

                                                                                               S _пр=3 × 4

                                                                                               S _пр=12 см²

41. Как найти площадь квадрата?              Сторона прямоугольника: а = S _пр : в

                                                                       Пример:         в = 6 см

                                                                                               S _пр=18 см²

                                                                                               а = ?

                                                                                               а = S _пр : а     

                                                                                               а = 18 : 6

                                                                                               а = 3 см

42. Как найти периметр квадрата,              Площадь квадрата: S_кв = а × а

     если известна площадь, которая           Пример:                   а = 9 см

     равна: 4,9,16,25,36,49,64,81,                                                   S_кв = ?

     100 см?                                                                                      S_кв  = а × а

                                                                                                        S_кв  = 9 × 9       

                                                                                                        S_кв  =81см²

43. Как найти площадь по извест-             Сторону квадрата находим подбором:     

      ному периметру и стороне?                                                 S_кв  = а × а

                                                                       Пример:                 S_кв  =64 см², значит  а = 8 см,

                                                                       а затем находим    Р_кв = а × 4

                                                                                                      Р_кв = 8 × 4

                                                                                                      Р_кв = 32 см

44. Что такое    квадратный                                                       Р_пр = (а + в) × 2

      сантиметр?                                                                             а- неизвестна  

                                                                                                       а = Р_пр : 2 - а

                                                                                                      S= а ×  в

45. Что такое числитель?                             Квадрат со стороной один сантиметр – это

                                                                       квадратный сантиметр.

46.Что такое знаменатель?                         Число над чертой дроби показывает, сколько     

                                                                       взято равных долей от целого, и называется                                                                                         числитель.

47. Как найти дробь числа?                       Число под чертой дроби показывает, на                                                                                                  сколько долей разделено целое, и называется                                                                                        знаменателем.

48. Как найти число по дроби?                    Чтобы найти дробь числа нужно число разделить

                                                                         на знаменатель, а потом умножить на числитель.

49. Сколько в 1 м² = ? дм² ;                         Чтобы найти число по дроби, нужно число

      1 м² = ? см²; 1 дм² =? см²;                      разделить на числитель и умножить на                                                                                                   знаменатель.

50. Какие числа делятся на 2?                                в 1 м² = 100 дм²       

                                                                                   в 1 м² = 10000 см²

                                                                                    в 1 дм² = 100 см²     

51. Какие числа делятся на 3?                     На 2 делятся числа, которые оканчиваются на

                                                                        0, 2, 4, 6, 8 (четные числа)

                                                                        Пример: 826 : 2 + 413

                                                                                        827 : 2 – не делится

52. Какие числа делятся на 5?                     На 3 делятся числа, сумма которых делится

                                                                        на 3.

                                                                         Пример: 123  : 3 = 41

                                                                                         1+ 2 + 3= 6         

                                                                                         6  : 3  - делится

53. Какие числа делятся на 6?                     На 5 делятся числа, которые оканчиваются

                                                                        на 0 и 5.

                                                                        Пример:    900  : 5 = 180

                                                                                           1135 : 5 = 227   

54. Какие числа делятся на 9?                    На 6 делятся числа, которые делятся на 2 и 3.

                                                                       Пример:     216 : 6 = 36

                                                                                            216 : 2

                                                                                         и 2 + 1 + 6 = 9,9 : 3 - делится.

55. Какие числа делятся на 10,                    На 9 делятся числа, сумма цифр которых

      100, 1000?                                               делится на 9.

                                                                        Пример:    1818 : 9 = 202

                                                                                            1 + 8 + 1 + 8 = 18

                                                                                            18 : 9 – делится

 56.                                                                  На 10, 100, 1000 и т.д. (круглые числа).

                                                                        На круглые числа делятся такие числа, которые                                                                                    имеют на конце столько же нулей или больше,

                                                                        чем у делителя.

            Любому учителю хочется, чтобы его ученики писали грамотно, но для этого дети должны знать все правила и уметь применять их на практике. Чаще всего им этого делать не хочется, скучно. А, играя, соревнуясь по группам, или  по рядам дети хорошо усваивают учебный материал. 

            В процессе игры я обращаю внимание на громкость, выразительность чтения и, конечно, внимательность игроков. Если кто-то из учеников прослушал вопрос, я сама начинаю говорить ответ, тот ученик, у которого на карточке есть ответ он, подхватывает и до конца говорит правило. Если игра проходит в форме соревнования по группам или по рядам, то ученику, прослушавшему вопрос, ставится минус. Все карточки «Домино» пронумерованы. Это позволяет работать не со всеми карточками, а подбирать их по темам. Например, Тема: Глагол 4 класс (карточки с 46 по 60). Тема: Состав слова и правописание безударных гласных 3 класс (карточки с 7 по 20).В конце игры подводится итог. Побеждает та группа или тот ряд, игроки которых не получили минус. По времени игра может занимать 5 – 10 минут, но результат превосходит все ожидания. В «Домино» можно играть на индивидуально-групповых занятиях, факультативах, в группах продленного дня. Единственное пожелание учителям – хранить карточки у себя и раздавать их перед уроком. Ведь если потеряется хоть одна карточка, связь в «Домино» нарушается.

            Мои карточки по русскому языку печатались в газете «Первое сентября» в статьях «Лото по математике», «Лото по русскому языку» в № 40 – 96г, № 35 – 99г., по математике № 42 -96г, № 42 – 98г, но это было по программе 1 – 3 (занимались по учебнику русского языка автора Кустаревой). Вопросов там не было, просто были правила. Как хорошо, что появились вопросы в учебнике. Сейчас сменилась программа 1 – 4, сменились учебные книги, поэтому карточки «Лото» я переработала и назвала  «Домино». Во 2-ом классе – 30 карточек, в 3-ем классе - 40 карточек, а в 4-ом классе – 62 карточки. Внизу на карточке указаны страницы русского языка (Т.Г. Рамзаева), поэтому, когда ученик читает правило по карточке, дети могут не только слушать, но и следить по книге, происходит развитие слуховой и зрительной памяти. У учителя должна быть особая тетрадь для «Домино» с полными вопросами и ответами, чтобы в любую минуту помочь ученику. Вопросы составлены по темам программы русского языка, в полном соответствии с программой  курса русского языка, утвержденной министерством образования России. Карточки подготавливаю я сама, записываю правила печатными буквами, а потом наклеиваю на картон. И так после каждого изученного правила. На это уходит очень много свободного времени учителя, но детям легче читать крупный печатный текст.

«Домино» по русскому языку для 2 класса.

(теоретический материал)

«Домино» по русскому языку для 3 класса.

1. Что такое предложение?
Вопрос   2. Какие слова пишутся с большой буквы?	Предложение – это слово и несколько слов, которые связаны по смыслу и выражают законченную мысль.   Утро. Ребята  спешат в школу.                                                                стр.5

«ДОМИНО» по русскому языку для 4 класса.

(теоретический материал)

             Мои карточки для устного счета, которые печатались в газете «Первое сентября», помогут детям приобрести прочные знания в 1-м классе, а во 2-м их можно использовать для повторения и закрепления пройденного материала. Они наглядно показывают учителю степень подготовки учеников.

            Бывает так, что ребенок очень хорошо понимает трудный материал, а простой долго до него не доходит. Поэтому, чтобы не было пробелов в знаниях, я составила карточки от простого к сложному. Веду черновой журнал. Оценки ставлю строго: за 1 ошибку – «4», за 2 ошибки – «3», за 3 ошибки – незачет.

            При таком учете, хорошо вижу, что конкретно не понял каждый ученик. И на основе этого строю индивидуальную работу. Например, работаем над карточками с 1 - 10. Когда в классе появятся ученики, которые решили все десять карточек на «4» и «5», - они будут «учителями». А что делают эти «учителя»? Они проверяют в карточках ответы, ставят оценки и записывают их в список, который висит на доске.

            Это надо видеть,  как «дети-учителя» проверяют карточки. Пересчитывают очень придирчиво. Вычислительные навыки у них доходят до автоматизма, и никогда не завысят и не занизят оценку, строго поставят по установленным нормам.

           Успех обучения математике во многом будет зависеть  от того, в какой мере, сознательно или целенаправленно, учитель организует работу детей, в какой мере, он сумеет заинтересовать их занятиями, внести в уроки материал, способный привлечь как

не произвольное так и произвольное внимание детей, вызвать у них живой интерес и стремление преодолевать встающие перед ними трудности.

            В ходе контроля проверяется соответствие достигнутых  учащимися знаний и умений, навыков установленных государственным эталоном, а оценка выражает реакцию на степень и качество этого соответствия  (отлично, хорошо, удовлетворительно, плохо). Таким образом, в конечном счете, система контроля и оценка для учителя становится инструментом оповещения. Учет знаний  очень помогает  в контроле знаний учащихся. Я знаю конкретно про каждого ученика, что он не знает и чем с ним отдельно заниматься, какое давать индивидуальное задание на дом. На это, конечно, уходит очень много свободного времени, не считая проверки тетрадей и написания планов.                        

            Работа проходит на листочках, которые потом сразу уничтожаются, учитель должен быть уверен на 100%, что ни один пример не списан.

            Мои карточки имеют свою специфику. Я составила 30 видов примеров. Конечно, много зависит от набора класса. В одном классе эти карточки дети почти все выполнили в конце первого класса (с опережением). Во втором выпуске смогли выполнить только в середине второго класса (без опережения).

            № 1

            3 + 9 =                        2 + 9 =                        9 + 2 =

            7 + 8 =                        4 + 8  =                       9 + 4 =

            6 + 5 =                        7 + 7 =                        5 + 8 =

            4 + 7 =                        7 + 5 =                        8 + 8 =

            8 + 4 =                        8 + 3 =                        8 + 9 =

           № 2

            11 –  8 =                     12 –  9 =                     14 –  5 =

            13 –  6 =                     14 –  7 =                     11 –  4 =

            15 –  9 =                     16 –  8 =                     16 –  7 =

            17 –  8 =                     18 –  9 =                     17 –  8 =

            12 –  6 =                     15 –  7 =                     18 –  9 =                    

                        Контроль и самоконтроль – важные условия формирования вычислительных навыков. Важное место в курсе математики начальных классов занимают арифметические действия. Это объясняется не только значимостью вычислительных навыков для дальнейшего обучения в средней школе, но и их практической необходимостью в жизни людей.

            Таким образом, повышение качества обучения математике в начальных классах в значимой мере зависит от прочных вычислительных навыков сформированных у младших школьников.

            При обучении младших школьников математике одно из центральных мест занимает формирование прочных навыков табличного сложения, вычитания, умножения и деления. Эти навыки должны формироваться осознанно и прочно, так как на их базе строится весь курс обучения математике.

            Необходимо добиваться, чтобы каждый ученик непременно усваивал программный материал, отведенный для данного урока, ибо все  последующие знания, умения и навыки по математике формируются на основе ранее изученного материала.

            Вычислительные навыки успешно формируются у учащихся при создании в учебном процессе определенных условий. Прежде всего, это знание учеником последовательности действий, умение выделить главное, соблюдение на уроке неспешного темпа  в овладении требованиями учебной программы, особенно на этапе первичного закрепления учебного материала.

            Кроме того, необходимо постоянно поддерживать активный интерес у детей, продумывать положительное его подкрепление. Принципиальное значение имеет правильное распределение упражнений во времени и их разнообразии.

            Понятно, что на каждом уроке постоянно должны иметь место отработка навыков контроля, самоконтроля и самооценки. Многочисленные факты и наблюдения, связанные с уроками математики, свидетельствуют, что в педагогической практике выработке у каждого ученика необходимых навыков контроля, самоконтроля уделяется, крайне недостаточное внимание, а нередко просто игнорируется.

            Обучение контролю и самоконтролю должно иметь место при объяснении нового материала и его закрепление, что будет способствовать процессу формирования вычислительных навыков высокой эффективности, делать их осознанными, прочными, безошибочными и способными к широкому переносу на более сложные вычислительные приемы. Наилучших результатов в выработке умений контроля и самоконтроля при формировании вычислительных навыков добиваются те учителя, которые предусматривают и осуществляют эту работу непосредственно на самом уроке.

            В ходе индивидуального и фронтального опросов, в беседах с учениками учитель спрашивает детей, какими конкретно приемами  они пользуются, как рассуждают, производя определенные вычисления. Если не проводить такой работы систематически, то ученики не смогут объяснить даже свои правильные ответы. Учителю крайне нелегко будет выявить случаи, когда ученик пользуется нерациональными вычислительными приемами.

          Я хочу поделиться опытом работы ведения учета и контроля знаний учащихся табличного деления и умножения. Формирование прочных вычислительных навыков табличного умножения и деления – одна из самых сложных задач курса математики начальных классов. Прежде чем приступить к составлению, заучиванию таблиц умножения и деления дети должны понять смысл действий умножения и деления, переместительное свойство умножения, взаимосвязь компонентов и результатов действий.

            Центральная задача третьего года обучения – изучение таблицы умножения и деления. На данном этапе необходимо организовать работу так, чтобы ученики твердо знали таблицу умножения и приобретали необходимую беглость вычислений при решении соответствующих случаев деления. От усвоения этих знаний зависит, как учащиеся будут применять эти приемы вне табличного умножения и деления. Некоторым детям с трудом дается таблица умножения, а воспроизведение табличных случаев деления происходит еще сложнее. И это понятно, прежде чем назвать ответ, ведь дети должны сначала вспомнить пример на умножение и быстро уметь применить его к делению. Учителя начальных классов применяют много наглядности, затрачивают много сил и труда, чтобы у детей были прочные знания таблицы умножения и деления.

            Для того, чтобы опросить учителю весь класс и знать конкретно сколько примеров и какую таблицу не знает ученик, требуется очень много времени. При систематическом контроле хорошо видно, что не знает каждый ученик. На основании этого учитель уже строит индивидуальную работу. За один урок при помощи таких перфокарт, которые я составила, можно опросить всю таблицу на деление и умножение  каждого ученика.

            В своем черновом журнале «Учет знаний учащихся», я выставляю оценки за таблицу на деление и умножение. Оценки ставлю строго: за 1 ошибку в таблице на 5 ставлю оценку «4», за 2 ошибки – «3», за 2 ошибки – «3», за 3 ошибки – незачет. Кроме того, я веду черновой журнал, результаты детей вывешиваю, на следующий день, на доске. Дети видят свои результаты, и там где не стоит оценка (т.е. незачет), ученик знает, что конкретно учить. Дети исправляют незачет. Они работают в парах. У каждого ученика и учителя есть карточки на умножение и деление. Они спрашивают друг друга. Примеры с неправильными ответами откладывают в сторону. Затем работают только с карточками, где были ошибки.  На обратной стороне карточки пишем ответ карандашом, чтобы ответ не просвечивал. По таким карточкам дети дома могут заниматься без помощи родителей. Ребенок сидит и считает пример на карточке, говорит ответ, а потом сверяется с ответом, на обратной стороне, а если проводить такую работу по каждой таблице (на 2,3,4,5,6,7,8,9), а потом по общей, то у детей будут формироваться прочные вычислительные навыки табличного деления и умножения. Они будут стараться исправить тройки и четверки только на «5».

            Ребятам, не надо говорить какую таблицу надо решать, они сами найдут в перемену перфокарту с той таблицей, которая ему нужна и быстро напишут ответы в тетради.

В  моих перфокартах  таблица записана вразброс, а учителю при проверке классной работы нужно поставить отдельную оценку за таблицу и не забыть выставить ее в журнал по учету знаний и выставить оценку на классное табло.

            Такая работа оправдывает себя. Дети учат таблицу без принуждения, они знают, что кто ответил всю таблицу, например таблицу на 2-4 столбика, (2 столбика на умножение, 2 столбика на деление) напротив его фамилии учитель поставит красный флажок. Они очень гордятся этим, стараются быть первыми, потому что первые станут «учителями» на следующем уроке.

            Перфокарты экономят время ученика и учителя, ребенок накладывает перфокарту на тетрадь  и пишет только одни ответы через запятые, а у учителя ответы к перфокартам под рукой.  Работа с перфокартами печаталась в журнале «Начальная школа» № 10, 2006г.

ПЕРФОКАРТЫ НА УМНОЖЕНИЕ

            Умножение с числом 2

          Умножение с числом 3

и т.д.

ПЕРФОКАРТЫ НА ДЕЛЕНИЕ

            Деление с числом 2

         Деление с числом 3

                           и т.д.                      

            После опроса знаний таблицы сразу видно, кто не знает какую таблицу.

На уроке, дети садятся парами, «учитель-ученик», и в устном опросе «учитель» выясняет какие именно примеры не знают их ученики, и записывают эти примеры в рабочую тетрадь, а учитель записывает эти примеры в свою тетрадь с планом, и на устном счете спрашивает при фронтальном опросе именно те примеры, и тех учеников, которые ошибались на прошлом уроке.

             На устном счете, я быстро показывают карточки с примерами на деление и умножение, не называя их, дети говорят только одни  ответы. Это экономит время на уроке, нет лишних слов, только четкие ответы.

            Также провожу соревнования, кто больше и правильно ответит примеров за 1 минуту.

            Карточки с примерами дети раскладывают на партах. Я включаю секундомер, дети с первого варианта отвечают примеры. Затем они считают, сколько ответили за 1 минуту, я записываю это  количество примеров в журнал по учету знаний. Аналогичная работа проводится со вторым вариантом. Затем мы с ребятами выясняем, кто занял 1, 2 , 3 места.

По окончании педагогического института, это более 30 лет назад, я не вела такого строгого учета знаний, поэтому не была уверена в хороших результатах ответа детей. Проводила контрольные работы, а сколько будет ошибок на вычисление, как они решат? Я точно не знала.

Сейчас конкретно знаю про каждого ученика, что он не знает, и тогда, когда родители приходят и спрашивают об успехах ученика, я могу дать полную картину успеваемости каждого ребенка, какой тип примеров не понял ребенок, и какой тип задачи он не может решать.   

Список литературы.

1.        Газета «Начальная школа» (прил. к газете «Первое сентября за 1996-         2003г.г.)

2.        Т.В.Шклярова, Я.И.Картунова «Справочное пособие для начальных классов».

3.        О.В.Узорова, Е.А.Нефедова «2000 задач и примеров по математике» М., АСТ Астрель, 2003г.

4.        М.И. Моро, М.А.Бантова, Г.В.Бельтюкова, С.И.Волкова, С.В.Степанова. Учебники математика с 1-го по 4-ый классы. М., Просвещение, 2003г.

5.        Т.Г.Рамзаева. Учебники русского языка с 1-го по 4-ый классы. М., «Дрофа», 2000г.