
Системы счисления (СС)
I. Двоичная система счисления.
Как устроено число в десятичной СС: 57910=5·102+7·101+9·100 (a0 1,a0).
В любой другой позиционной системе счисления числа устроены точно таким же образом. Только будет меняться набор цифр и основание системы счисления.
1. Перевод чисел из двоичной в десятичную систему счисления.
Дано двоичное число 1101112. Индекс означает принадлежность числа к двоичной СС. Переведём его в десятичную систему счисления. На каждой позиции стоит цифра числа перед соответствующей степенью основания системы счисления. В данном случае имеем следующее:
Показатели степени «2»: 5 4 3 2 1 0
Цифры числа: 1 1 0 1 1 1
![]() 1101112=1·25+1·24+0·23+1·22+1·21+1·20=5510
1101112=1·25+1·24+0·23+1·22+1·21+1·20=5510
Очевидно, что слагаемые, у которых в произведении есть «0» на сумму влияния не окажут. Для удобства можно все слагаемые из степеней «2» записать столбиком, а затем сложить:
|
+ |
32 16 4 2 1 —— 55 |
Таким образом, мы получили число в десятичной СС.
2. Перевод чисел из десятичной в двоичную систему счисления.
Возьмём то же самое десятичное число 55 и переведём его в двоичную систему счисления. Для этого надо последовательно делить его на 2 и в обратном порядке собирать остатки от деления. Начинаем с последней единицы!
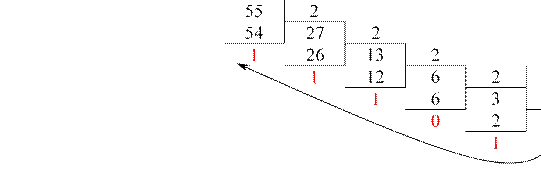
Выписав остатки, получим наше исходное число в двоичной системе счисления:
1101112
Задание для самостоятельного решения.
Задание №1.
Переведите двоичное число 1111101112 в десятичную СС и обратно. Смотри ответ в конце.
3. Сложение и умножение целых чисел в двоичной системе счисления.
Для выполнения этих операций составим соответствующие таблицы умножения и сложения. По горизонтали и вертикали выпишем цифры двоичной СС. На пересечении напишем результат арифметических операций.
|
х |
0 |
1 |
|
+ |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
1 |
|
|
1 |
0 |
1 |
1 |
1 |
10 |
Если с умножением понятно, то со сложением надо разобраться. Вспомним привычную нам десятичную СС. При сложении, например, «7» и «3» мы получим число, которое невозможно в этой СС записать одной цифрой. Поэтому в справа пишем «0», а слева «1». Ровно точно также следует поступить и с числом в любой другой СС в том числе и в двоичной. Исчерпав цифры для записи чисел, при сложении 1+1 следует в правый разряд записать «0», а в следующий «1».
По-другому: переведём двоичное число 102 в десятичную СС.
102=1·21+0·20=2+0=210.
То есть эта та самая привычная нам десятичная «двойка».
Рассмотрим сложение трёх, четырёх, пяти, шести и семи единиц:
1+1+1=10+1=11
1+1+1+1=10+10=100
1+1+1+1+1=100+1=101
1+1+1+1+1+1=101+1=110
1+1+1+1+1+1+1=110+1=111
Заметим, что это не привычные нам «одиннадцать», «сто», «сто один», «сто десять» и «сто одиннадцать». Это двоичные «3», «4», «5», «6» и «7». А читать число следует по цифрам: «один один», «один ноль ноль» и т.д.
Перейдём к примерам.
Сложим и перемножим два двоичных числа. После этого все числа переведём в десятичную СС и сделаем проверку, сложив и перемножив эти числа в десятичной СС.
Воспользуемся нашими предыдущими результатами. Складывать и умножать будем точно также, как и в десятичной СС поразрядно в столбик. При сложении двух единиц результат под этим разрядом 0, а единица пойдёт в следующий разряд. Складывая три единицы, получим 11. То есть правую единицу напишем под этим разрядом, а левая перейдёт в следующий.
1 1 1 1 1 1 1
1 1 1 0 1 0 1 12
+
1 1 1 1 1 12
![]() 1 0 0
1 0 0
Теперь переведём все три числа в десятичную СС и сделаем проверку:
Первое число Второе число Результат
7 6 5 4 3 2 1 0 5 4 3 2 1 0 8 7 6 5 4 3 2 1 0
1 1 1 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0 1 0 1 0
|
+
|
128 32 64 16 32 8 8 4 + 2 2 1 1 —— —— 23510 6310 |
|
256 32 + 8 2 —— 29810 |
|
|
1 1 1 0 1 0 1 1 + 2
|
= = |
23510 6310 |
![]()
1 0 0 1 0 1 0 1 02 = 29810
Теперь перемножим те же двоичные числа:
х 1 1 1 0 1 0 1 12
1 1 1 1 1 12
![]() 11 1 1 1 1 1
1
11 1 1 1 1 1
1
1 1 1 0 1 0 1 1
1 1 1 0 1 0 1 1
1 1 1 0 1 0 1 1
+
1 1 1 0 1 0 1 1
1 1 1 0 1 0 1 1
1 1 1 0 1 0 1 1
![]() 1
1 0 1 0 12
1
1 0 1 0 12
Для проверки осталось перевести результат в десятичную систему счисления, затем перемножить 235 и 63.
13 12 11 10 9 8 7 6 5 4 3 2 1 0
1 1 1 0 0 1 1 1 0 1 0 1 0 12
8192 235 х
4096 63
![]()
2048 705
![]() 256
+
256
+
128
+ 64
16
4
1
——
1480510
Результаты совпали, что свидетельствует о том, что умножение в двоичной СС выполнено верно.
Задание для самостоятельного решения.
Задание №2.
Сложите и умножьте два двоичных числа 110110112 и 1111012. Исходные числа и результаты арифметических действий переведите в десятичную СС. Проделайте те же операции с десятичными числами и сравните получившиеся значения. Смотри ответ в конце.
II. Восьмеричная система счисления.
Как уже было сказано, любая позиционная система счисления устроена одинаково. Разница заключается в количестве цифр, используемых для записи чисел (или в основании системы счисления). В восьмеричной СС соответственно всего 8 цифр для записи чисел: от 0 до 7. Следующее за «7» число уже будет двузначным 108. Но это не 1010, а восьмеричное число «8».
1. Перевод чисел из восьмеричной в десятичную систему счисления.
Дано число 65728. Индекс означает принадлежность числа к восьмеричной СС. Переведём его в десятичную систему счисления. На каждой позиции стоит цифра числа перед соответствующей степенью основания системы счисления. В данном случае перед числом «8» в соответствующей степени. Подпишем слева направо над данным числом показатели соответствующих степеней восьмёрки, начиная с нуля:
Показатели степени «8»: 3 2 1 0
Цифры числа: 6 5 7 2
То есть: 65728=6·83+5·82+7·81+2·80=345010
Умножим цифры числа на степени «8». Результаты запишем в столбик и сложим. Получившаяся сумма и будет числом в десятичной СС.
6·83 = 3072
5·82 = 320
+ 7·81 = 56
2·80 = 2
——
3450
2. Перевод чисел из десятичной в восьмеричную систему счисления.
Возьмём то же самое десятичное число 3450 и переведём его в восьмеричную систему счисления. Для этого надо последовательно делить его на 8 и в обратном порядке собирать остатки от деления. Начинаем с последней цифры!
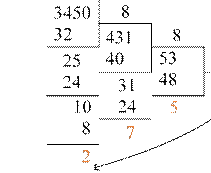
Выписав остатки, получим наше исходное число в восьмеричной системе счисления: 65728
Задание для самостоятельного решения.
Задание №3.
Переведите восьмеричное число 310758 в десятичную СС и обратно. Смотри ответ в конце.
3. Сложение и умножение целых чисел в восьмеричной системе счисления.
Для выполнения этих операций составим соответствующие таблицы умножения и сложения. По горизонтали и вертикали выпишем цифры восьмеричной СС. На пересечении напишем результат арифметических операций.
|
Таблица сложения |
|
Таблица умножения |
||||||||||||||||
|
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
2 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
11 |
2 |
0 |
2 |
4 |
6 |
10 |
12 |
14 |
16 |
|
|
3 |
3 |
4 |
5 |
6 |
7 |
10 |
11 |
12 |
3 |
0 |
3 |
6 |
11 |
14 |
17 |
22 |
25 |
|
|
4 |
4 |
5 |
6 |
7 |
10 |
11 |
12 |
13 |
4 |
0 |
4 |
10 |
14 |
20 |
24 |
30 |
34 |
|
|
5 |
5 |
6 |
7 |
10 |
11 |
12 |
13 |
14 |
5 |
0 |
5 |
12 |
17 |
24 |
31 |
36 |
43 |
|
|
6 |
6 |
7 |
10 |
11 |
12 |
13 |
14 |
15 |
6 |
0 |
6 |
14 |
22 |
30 |
36 |
44 |
52 |
|
|
7 |
7 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
7 |
0 |
7 |
16 |
25 |
34 |
43 |
52 |
61 |
|
Перейдём к примерам.
Возьмём два произвольных восьмеричных числа: 57328 и 2658. Сложим их в восьмеричной СС, затем перемножим. Исходные числа и результаты арифметических действий переведём в десятичную СС и выполним проверку.
1 1
5 7 3 2
![]() +
+
6 2 1 7
2+5 дадут «7». При сложении 3+6 получим «11». Поэтому в этот разряд пишем правую 1, а левая единица пойдёт в следующий разряд. Далее складываем 7+1=10 и 10+2=12. В этот разряд пишем «2», в следующий пойдёт «1». Наконец, 1+5 это «6». Переведём все три числа из восьмеричной в десятичную СС.
57328=5·83+7·82+3·81+2·80=303410 2658=2·82+6·81+5·80=18110 62178=6·83+2·82+1·81+7·80=321510
2560 128 3072
448 + 48 128
+ 24 5 + 8
![]()
2 181 7
![]()
![]()
1 1
+ 5 7 3 28 = 3 0 3 410
![]()
![]() =
=
6 8 = 3 10
Выполнив сложение в десятичной СС, получим тот же самый результат.
Перейдём к умножению. Перемножим те же числа в восьмеричной СС, воспользовавшись составленной нами таблицей умножения.
1 5 2 1
4 2 1
5 7 3 2
х
2 6 5
![]()
2 1
1 3 5 5 0 2
+ 1 4 3 4 3 4
Умножаем как в десятичной СС: сначала на первую цифру числа, записанного снизу, затем на вторую со сдвигом на разряд и точно также на третью.
Посмотрим детально, как мы умножали верхнее число на «5». Смотрим по таблице сколько будет 2·5. Это восьмеричное число «12». Поэтому в первый разряд запишем «2», а «1» запомним, добавив её к следующему разряду. Дальше умножаем 3·5. Результат «17», да ещё + «1». 1+7 даст «10», поэтому 17+1=20. «0» пишем, «2» в уме. 5·7=43 и + «2». То есть «45». «5» пишем «4» в уме. Наконец, 5·5=31 и + «4». Получим «35».
Аналогичным образом умножаем на оставшиеся две цифры. Затем производим сложение, пользуясь таблицей сложения для восьмеричной СС.
Осталось перевести получившееся восьмеричное число в десятичную СС, выполнить умножение в десятичной СС и сверить результаты.
Показатели степени «8»: 6 5 4 3 2 1 0
Цифры числа: 2 0 6 0 4 4 2
![]()
![]() 20604428=2·86+0·85+6·84+0·83+4·82+4·81+2·80=54915410
20604428=2·86+0·85+6·84+0·83+4·82+4·81+2·80=54915410
2·86 = 524288
6·84 = 24576
+ 4·82 = 256
4·81 = 32
2·80 = 2
—————
549154 Умножим десятичные числа: 3034·181.
3 0 3 4
1 8 1
![]()
1
3 0 3 4
+ 2 4 2 7 2
![]() 5 4
5 4
Результаты сошлись. Значит умножение в восьмеричной СС мы сделали верно. Задание для самостоятельного решения.
Задание №4.
Сложите и умножьте два восьмеричных числа 35728 и 6148. Исходные числа и результаты арифметических действий переведите в десятичную СС. Проделайте те же операции с десятичными числами и сравните получившиеся значения. Смотри ответ в конце.
III. Шестнадцатеричная система счисления.
В отличии от предыдущих систем счисления, где количество цифр для записи чисел было меньше десяти, в шестнадцатеричной СС их, соответственно, шестнадцать, то есть больше 10. Поскольку арабских цифр всего десять, в качестве недостающих шести выбрали первые заглавные буквы латинского алфавита. То есть набор цифр в этой СС выглядит так:
10 11 12 13 14 15
0 1 2 3 4 5 6 7 8 9 A B C D E F
Поскольку наше мышление жёстко привязано к десятичной СС для удобства над каждой буквой поставим соответствующее десятичное число.
1. Перевод чисел из шестнадцатеричной в десятичную систему счисления.
Дано число AD7E16. Индекс означает принадлежность числа к шестнадцатеричной СС. Переведём его в десятичную систему счисления. На каждой позиции стоит цифра числа перед соответствующей степенью основания системы счисления. В данном случае перед числом «16» в соответствующей степени. Подпишем слева направо над данным числом показатели соответствующих степеней числа «16», начиная с нуля:
Показатели степени «16»: 3 2 1 0
Цифры числа: A D 7 E
То есть: AD7E16=10·163+13·162+7·161+14·160= 4441410
Умножим цифры числа на степени «16». Результаты запишем в столбик и сложим. Получившаяся сумма и будет числом в десятичной СС.
10·163 = 40960
13·162 = 3328
+ 7·161 = 112
14·160 = 14
———
44414
2. Перевод чисел из десятичной в шестнадцатеричную систему счисления.
Возьмём то же самое десятичное число 44414 и переведём его в шестнадцатеричную систему счисления. Для этого надо последовательно делить его на 16 и в обратном порядке собирать остатки от деления. Начинаем с последней цифры!
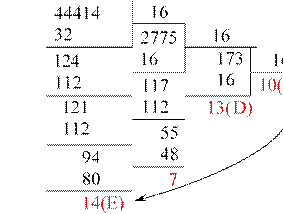
Выписав остатки, получим наше исходное число в шестнадцатеричной системе счисления:
AD7E16 Задание для самостоятельного решения.
Задание №5.
Переведите шестнадцатеричное число 9EFA16 в десятичную СС и обратно. Смотри ответ в конце.
3. Сложение и умножение целых чисел в шестнадцатеричной системе счисления.
Для выполнения этих операций составим соответствующие таблицы умножения и сложения. По горизонтали и вертикали выпишем цифры шестнадцатеричной СС. На пересечении напишем результат арифметических операций.
Таблица сложения
|
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
A |
B |
C |
D |
E |
F |
||||||||||||
|
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
|
|
2 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
|
|
3 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
|
|
4 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
|
|
5 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
|
|
6 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
7 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
8 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
|
9 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
10 |
A |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
11 |
B |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1A |
|
12 |
C |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1A |
1B |
|
13 |
D |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1A |
1B |
1C |
|
14 |
E |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1A |
1B |
1C |
1D |
|
15 |
F |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1A |
1B |
1C |
1D |
1E |
Таблица умножения
|
х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
A |
B |
C |
D |
E |
F |
||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
2 |
0 |
2 |
4 |
6 |
8 |
A |
C |
E |
10 |
12 |
14 |
16 |
18 |
1A |
1C |
1E |
|
|
3 |
0 |
3 |
6 |
9 |
C |
F |
12 |
15 |
18 |
1B |
1E |
21 |
24 |
27 |
2A |
2D |
|
|
4 |
0 |
4 |
8 |
C |
10 |
14 |
18 |
1C |
20 |
24 |
28 |
2C |
30 |
34 |
38 |
3C |
|
|
5 |
0 |
5 |
A |
F |
14 |
19 |
1E |
23 |
28 |
2D |
32 |
37 |
3C |
41 |
46 |
4B |
|
|
6 |
0 |
6 |
C |
12 |
18 |
1E |
25 |
2A |
30 |
36 |
3C |
42 |
48 |
4E |
54 |
5A |
|
|
7 |
0 |
7 |
E |
15 |
1C |
23 |
2A |
31 |
38 |
3F |
46 |
4D |
54 |
5B |
62 |
69 |
|
|
8 |
0 |
8 |
10 |
18 |
20 |
28 |
30 |
38 |
40 |
48 |
50 |
58 |
60 |
68 |
70 |
78 |
|
|
9 |
0 |
9 |
12 |
1B |
24 |
2D |
36 |
3F |
48 |
51 |
5A |
63 |
6C |
75 |
7E |
87 |
|
|
10 |
A |
0 |
A |
14 |
1E |
28 |
32 |
3C |
46 |
50 |
5A |
64 |
6E |
78 |
82 |
8C |
96 |
|
11 |
B |
0 |
B |
16 |
21 |
2C |
37 |
42 |
4D |
58 |
63 |
6E |
79 |
84 |
8F |
9A |
A5 |
|
12 |
C |
0 |
C |
18 |
24 |
30 |
3C |
48 |
54 |
60 |
6C |
78 |
84 |
90 |
9C |
A8 |
B4 |
|
13 |
D |
0 |
D |
1A |
27 |
34 |
41 |
4E |
5B |
68 |
75 |
82 |
8F |
9C |
A9 |
B6 |
C3 |
|
14 |
E |
0 |
E |
1C |
2A |
38 |
46 |
54 |
62 |
70 |
7E |
8C |
9A |
A8 |
B6 |
C4 |
D2 |
|
15 |
F |
0 |
F |
1E |
2D |
3C |
4B |
5A |
69 |
78 |
87 |
96 |
A5 |
B4 |
C3 |
D2 |
E1 |
Перейдём к примерам.
Возьмём два произвольных шестнадцатеричных числа: B5916 и FCD16. Сложим их в шестнадцатеричной СС, затем перемножим. Исходные числа и результаты арифметических действий переведём в десятичную СС и выполним проверку.
1 1
B 5 9
+
F C D
1 B 2 6
9+D дадут «16». «6» пишем, «1» в уме. При сложении 5+С получим «11» да ещё «1», то есть «12». «2» пишем «1» в уме. Наконец, B+F+1 это «1B».
Переведём все три числа из шестнадцатеричной в десятичную СС.
B5916=11·162+5·161+9·160=290510 FCD16=15·162+12·161+13·160=404510
|
+ |
11·162 = 2816 5·161 = 80 |
|
+ |
15·162 = 12·161 = |
3840 192 |
![]() 9·160
= 9 13·160 =
9·160
= 9 13·160 =
![]()
1B2616=1·163+11·162+2·161+6·160=695010
1·163 = 4096
11·162 = 2816
+ 2·161 = 32
![]() 6·80 =
6·80 =
|
|
|
|
1 1 1 |
|
|
B 5 9 + 16 = 2 |
9 0 510 |
![]() F
C D16 =
F
C D16 =
1 B 2 616 = 10
Выполнив сложение в десятичной СС, получим тот же самый результат.
Перейдём к умножению. Перемножим те же числа в восьмеричной СС, воспользовавшись составленной нами таблицей умножения.
5 8
4 7
B 5 9
х
F C D
![]()
1 1 1
9 3 8 5
+ 8 8 2 C
A A 3 7
B 3 4 D 4 5
Умножаем как в десятичной СС: сначала на первую цифру числа, записанного снизу, затем на вторую со сдвигом на разряд и точно также на третью.
Посмотрим детально, как мы умножали верхнее число на «D». Смотрим по таблице сколько будет 9·D. Это шестнадцатеричное число «75». Поэтому в первый разряд запишем «5», а «7» запомним, добавив её к следующему разряду. Дальше умножаем 5·D. Результат «41», да ещё + «7». Получим «48». «8» пишем, «4» в уме. B·D=8F и + «4». То есть «93».
Аналогичным образом умножаем на оставшиеся две цифры. Затем производим сложение, пользуясь таблицей сложения для шестнадцатеричной СС.
Осталось перевести получившееся шестнадцатеричное число в десятичную СС, выполнить умножение в десятичной СС и сверить результаты.
Показатели степени «16»: 5 4 3 2 1 0
Цифры числа: B 3 4 D 4 5
B87A4516=11·165+3·164+4·163+13·162+4·161+5·160=1175072510
11·1048576 = 11534336
3·65536 = 196608
+ 4·4096 = 16384
13·256 = 3328
4·16 = 64
5·1 = 5
—————
11750725
Умножим десятичные числа: 2905·4045=11750725.
3 2
3 2
4 2
х 2 9 0 5
4 0 4 5
1
1 4 5 2 5
+ 1 1 6 2 0
![]() 7 2 5
7 2 5
Результаты сошлись. Значит умножение в восьмеричной СС мы сделали верно.
Задание для самостоятельного решения.
Задание №6.
Сложите и умножьте два шестнадцатеричных числа 8DE и 3F. Исходные числа и результаты арифметических действий переведите в десятичную СС. Проделайте те же операции с десятичными числами и сравните получившиеся числа. Смотри ответ в конце.
Ответы к заданиям для самостоятельного решения
№1: 1111101112=50310.
№2:
110110112 + 1111012 = 1000110002 21910 + 6110 = 28010
110110112 · 1111012 = 110100001011112 21910 · 6110 = 1335910
№3: 310758 = 1286110.
№4:
35728 + 6148 = 44068 191410 + 39610 = 231010
35728 · 6148 = 27102708 191410 · 39610 = 75794410
№5: 9EFA16 = 4069810.
№6:
8DE 16 + 3F 16 = 91D16 227010 + 6310 = 231010
8DE 16 · 3F 16 = 22EA28 227010 · 6310 = 14301010
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.