
СЛОЖНЫЕ
ТЕМЫ ЭЛЕКТРОДИНАМИКИ
§1. Теорема Остроградского-Гаусса.
Вспомним для начало некоторые понятия:
1. Линейная плотность заряда. Используется для описания распределения заряда по нити:

где: L – длина нити. Измеряется в Кл/м.
2. Поверхностная плотность заряда. Используется для описания распределения заряда по поверхности тела:
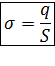
где: S – площадь поверхности тела. Измеряется в Кл/м2.
3. Объемная плотность заряда. Используется для описания распределения заряда по объему тела:

где: V – объем тела. Измеряется в Кл/м3.
Для понимания теоремы Остроградского-Гаусса
(далее будем просто говорить теорема Гаусса) введем новую физическую величину,
характеризующую электрическое поле – поток
Φ вектора напряженности электрического поля (обратите
внимание в 11 классе аналогично вводится поток вектора магнитной индукции).
Пусть в пространстве, где создано электрическое поле, расположена некоторая
достаточно малая площадка ΔS. Произведение модуля вектора ![]() на
площадь ΔS и на косинус угла α между вектором
на
площадь ΔS и на косинус угла α между вектором ![]() и
нормалью
и
нормалью ![]() к
площадке называется элементарным потоком
вектора напряженности через
площадку ΔS (рис. 1.3.1):
к
площадке называется элементарным потоком
вектора напряженности через
площадку ΔS (рис. 1.3.1):
|
ΔΦ = E ΔS cos α = En ΔS, |
где En –
модуль нормальной составляющей поля ![]() . Или просто:
. Или просто:
![]()
Теорема Гаусса утверждает:
Поток вектора напряженности
электростатического поля ![]() через
произвольную замкнутую поверхность равен алгебраической сумме зарядов,
расположенных внутри этой поверхности, деленной на электрическую постоянную
ε0.
через
произвольную замкнутую поверхность равен алгебраической сумме зарядов,
расположенных внутри этой поверхности, деленной на электрическую постоянную
ε0.
![]()
Рассмотрим несколько задач, причём, первые три теоретические и, в принципе, их результатом можно пользоваться при решении задач без вывода формул.
Задача 1. Найдите напряженность электрического поля, создаваемого равномерно заряженной бесконечной плоскостью. Поверхностная плотность заряда σ.
Решение:
Выберем поверхность прямого цилиндра, образующие которого перпендикулярны плоскости, а основания площадью S параллельны ей и находятся на равных расстояниях от плоскости.
Прежде всего,
заметим, что поток вектора напряженности через боковую поверхность цилиндра
равен нулю, так как во всех точках боковой поверхности векторы
напряженности ![]() и нормали
и нормали ![]() взаимно
перпендикулярны, следовательно, cosα=0.
взаимно
перпендикулярны, следовательно, cosα=0.
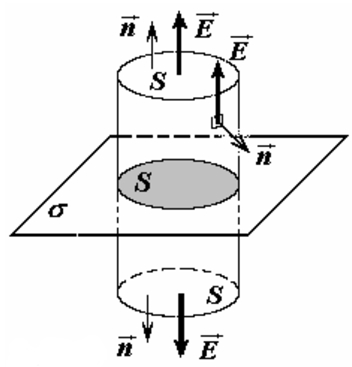
Поток через верхнее
основание цилиндра может быть записан в виде (![]()
Ф1=E*S,
так модуль напряженности поля на основании цилиндра постоянен, а по направлению совпадает с вектором нормали. Такое же значение имеет поток через нижнее основание.
Таким образом, суммарный поток вектора напряженности электрического поля через поверхность цилиндра равен
Ф= 2E*S.
С другой стороны, по теореме Гаусса
![]()
где ![]() – заряд,
заключенный внутри поверхности цилиндра:
– заряд,
заключенный внутри поверхности цилиндра:
![]() =σ*S.
=σ*S.
Следовательно,

Главная составляющая успеха – анализ симметрии поля, позволивший разумно выбрать поверхность, для использования теоремы Гаусса. Также обратите внимание, что напряженность данного поля одинакова во всех точках, следовательно, это поля является однородным. Подчеркнем, независимость напряженности поля от расстояния до плоскости h никак не следует из симметрии поля, это результат нашего расчета.
Примечание. Для плоскости,
заряженной отрицательно, результат будет таким же, лишь направление
вектора ![]() изменится на
противоположное.
изменится на
противоположное.
Задача 2. Найдите напряженность электрического поля, создаваемого в вакууме бесконечно длинной заряженной нитью с линейной плотностью заряда 𝜏.
Решение: Вычислим поток напряженности через цилиндр, ось которого совпадает с заряженной нитью
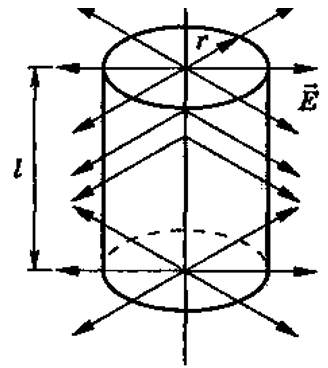
Радиус цилиндра r, а его высота l.
Из соображений
симметрии очевидно, что линии напряженности ![]() перпендикулярны
боковой поверхности цилиндра. Поэтому поток напряженности через боковую
поверхность цилиндра равен
перпендикулярны
боковой поверхности цилиндра. Поэтому поток напряженности через боковую
поверхность цилиндра равен
Ф=ES=E⋅2πrl,
Поток через основания цилиндра равен нулю (α=90°).
С другой стороны, по теореме Гаусса
![]()
,
где qВНУТР=τ⋅l – заряд, заключенный внутри цилиндра. Следовательно,
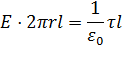
Или
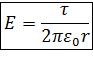
Задача 3. Найдите напряженность электрического поля, создаваемого равномерно заряженной сферой радиуса R. Суммарный заряд сферы q.
Решение: Опять начнем с рассмотрения симметрии поля. Очевидно, что поле, также как распределение зарядов имеет сферическую симметрию. Это означает, что модуль вектора напряженности зависит только от расстояния до центра сферы (или во всех точках, находящихся от центра сферы на одном расстоянии, модуль напряженности постоянен), а направление – радиальное, от центра сферы к точке наблюдения. Выберем в качестве замкнутой поверхности, к которой применим теорему Гаусса, сферу, концентрическую с заряженной оболочкой (рис.).
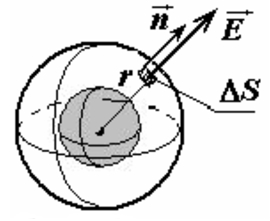
Пусть радиус
сферы r больше радиуса оболочки r>R. Тогда во
всех точках этой сферы вектор напряженности направлен вдоль нормали к
поверхности, а его модуль постоянен. Поэтому поток вектора напряженности ![]() через сферу равен
произведению модуля напряженности на площадь сферы
через сферу равен
произведению модуля напряженности на площадь сферы
Ф=E⋅S=E⋅4πr2.
По теореме Гаусса это поток равен
![]()
Следовательно,
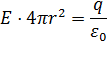
Значит
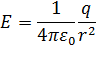
Или
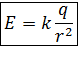
Полученная формула, соответствует формуле закона Кулона для точечного заряда, следовательно, вне сферы, поле равномерно заряженной сферы, совпадает с полем точечного заряда, помещенного в центре сферы.
Поле внутри заряженной сферической оболочки также должно обладать сферической симметрией. Поэтому, поток вектора напряженности электрического поля через сферу, концентрическую с заряженной оболочкой и расположенную внутри нее (рис.)
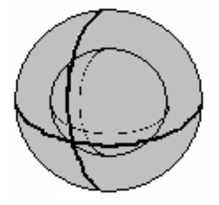
также выражается формулой
Ф=E⋅S=E⋅4πr2
Однако внутри этой сферы электрических зарядов нет, поэтому, из теоремы Гаусса следует, что напряженность поля внутри сферы равна нулю. Подчеркнем, если бы теорема Гаусса была не справедлива, то внутри равномерно заряженной оболочки существовало бы электрическое поле.
Таким образом, функция, описывающая напряженность поля равномерно заряженной сферы радиуса R, имеет вид:
![]()
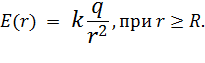
Примечание.
1) Очевидно, что для сферы, заряженной отрицательно, формулы остаются справедливыми, только векторы напряженности будут направлены в противоположные стороны (к центру сферы).
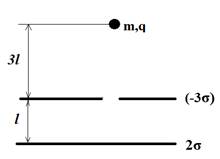 Задача
4. Имеются
две параллельные заряженные пластины с поверхностной плотностью зарядов −3σ
и
2σ
(σ>0),
расстояние между которыми l. В одной пластине сделано малое отверстие.
На расстоянии 3l от пластин напротив отверстия удерживают точечное тело
с зарядом q и массой m (q > 0).
Тело отпускают. Достигнет ли тело пластины с зарядом 2σ
и
если да, то какую скорость оно будет иметь около этой пластины? А если нет, то
на каком расстоянии от нее остановится? Краевыми эффектами пренебречь.
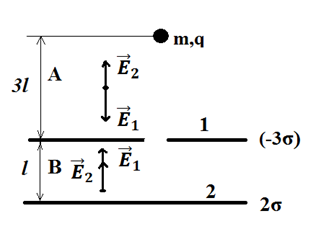
Задача
4. Имеются
две параллельные заряженные пластины с поверхностной плотностью зарядов −3σ
и
2σ
(σ>0),
расстояние между которыми l. В одной пластине сделано малое отверстие.
На расстоянии 3l от пластин напротив отверстия удерживают точечное тело
с зарядом q и массой m (q > 0).
Тело отпускают. Достигнет ли тело пластины с зарядом 2σ
и
если да, то какую скорость оно будет иметь около этой пластины? А если нет, то
на каком расстоянии от нее остановится? Краевыми эффектами пренебречь.
 Решение:
Решение:
Обозначим пластину с отверстием цифрой 1, без отверстия – 2. Электрическое поле в любой точке пространства создается зарядами обеих пластин. Найдем направление напряжённостей каждой пластины в областях А и В. Пользуясь тем, что напряженность поля пластины
![]()
По принципу суперпозиции находим напряженность поля в областях.
В области А:
![]()
Вектор суммарной
напряжённости ![]() направлен к пластине 1,
т.е. вниз на рисунке.
направлен к пластине 1,
т.е. вниз на рисунке.
В области В:
![]()
Вектор суммарной
напряжённости ![]() направлен к пластине 1,
т.е. вверх на рисунке.
направлен к пластине 1,
т.е. вверх на рисунке.
Работа поля над положительным зарядом q при его движении до нижней пластины равна алгебраической сумме работ придвижении в обоих областях. Заметим, что в области А работа поля положительная (положительное тело движется по направлению результирующего поля), а области В работа поля отрицательная (положительное тело движется против направления результирующего поля). Так как работа поля
![]()
Получим
![]()
Поскольку работа (*) отрицательна, заряд q не достигнет нижней пластины. Точку его остановки найдем по теореме об изменении кинетической энергии – при нулевой начальной и конечной скорости заряда работа поля до точки остановки равна нулю:
![]()
где x – расстояние от точки остановки до нижней пластины. Из последнего находим
![]()
Ответ: не достигнет,
остановится на расстоянии ![]() от
нижней пластины.
от
нижней пластины.
 Задача 5. Три
очень большие параллельные металлические пластины заряжены зарядами Q, 2Q
и 3Q (см. рисунок снизу слева). Найти заряды верхней и нижней
поверхности средней пластины. Краевыми эффектами пренебречь.
Задача 5. Три
очень большие параллельные металлические пластины заряжены зарядами Q, 2Q
и 3Q (см. рисунок снизу слева). Найти заряды верхней и нижней
поверхности средней пластины. Краевыми эффектами пренебречь.
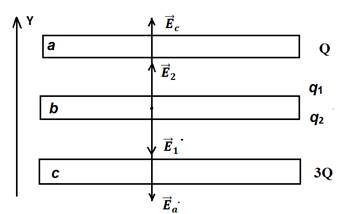 Решение: Пусть на верхней и нижней поверхностях средней
пластины распределены заряды q1 и q2 (см.
рисунок). Из закона сохранения электрического заряда имеем:
Решение: Пусть на верхней и нижней поверхностях средней
пластины распределены заряды q1 и q2 (см.
рисунок). Из закона сохранения электрического заряда имеем:
![]()
Дальне можно рассмотреть
суммарное поле внутри любой пластины, помня о том, что ![]() .
Рассмотрим среднюю пластину. Напряжённость поля пластины
.
Рассмотрим среднюю пластину. Напряжённость поля пластины
![]()
Применяя принцип суперпозиции полей в проекции на ось OY, получим:
![]()
Решая систему уравнений (1) и (2), получим:
![]()
Значит ![]() ,
, ![]() .
.
Ответ:![]() ,
,![]() .
.
Еще хотелось бы обратить внимание на задачи с концентрическими сферами.
Задача №6. Металлический шар радиусом R, имеющий заряд q, находится внутри диэлектрика с диэлектрической проницаемостью ε. Определите поляризационный заряд, возникающий в диэлектрике у поверхности заряженного шаpa, и поверхностную плотность поляризационного заряда.
Решение. Если бы вокруг шара не было диэлектрика, то он создавал бы в окружающем пространстве поле с напряженностью
![]()
где r >> R.
При наличии диэлектрика возникает поле с напряженностью
![]()
![]()
![]()
![]()
![]()
![]()
Разность
![]()
Понятно, что данная разность равна напряженности поля, которое создает поверхностный поляризационный заряд q', появляющийся возле заряженного шара (рис. 1). Заряд q' противоположен по знаку заряду q. Так как поляризационный заряд распределен равномерно по поверхности сферы, то
![]()
![]()
![]()
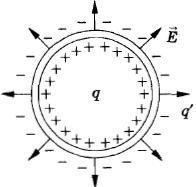
![]()
![]()
Рис. 1
Приравнивая выражения (1) и (2) , находим:
![]()
![]()
![]()
Примечание: Понимание данной задачи важно при решении подобных
задач. Отметим, что под зарядом![]() стоит
понимать и систему зарядов, находящихся внутри диэлектрического сферического
слоя.
стоит
понимать и систему зарядов, находящихся внутри диэлектрического сферического
слоя.
Задача №7.Металлический шар радиуса R окружен концентрической проводящей сферой радиуса 2R. к сфере прилегает слой твердого однородного диэлектрика с проницаемостью ε=2. Внешний радиус слоя 4R. Шар заземляют (заземляющий провод не касается сферы), а сфере сообщают заряд
q0= - 1,7 нКл. Найдите установившийся заряд шара q.
Решение:
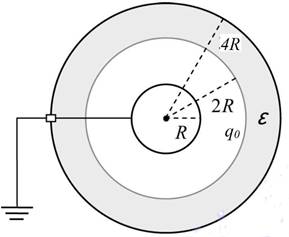 Обозначим заряд на одной поверхности диэлектрика (радиус 4R) Q, а на другой (2R) –Q.
Обозначим заряд на одной поверхности диэлектрика (радиус 4R) Q, а на другой (2R) –Q.
Потенциал внутри шара или сферы находится по формуле
![]()
Где R – радиус шара.
Так как шар заземлен, то потенциал внутри шара равен 0. Значит, пользуясь принципом суперпозиции полей, получаем:
![]()
Или
![]()
Или
![]()
Значит
![]()
Проводя рассуждения, аналогичные решению задачи №6, получим
![]()
Подставляя последнее в уравнение (*), получим
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:0,73 нКл.
§ 2. Законы Кирхгофа.
Прежде чем говорить о законах Кирхгофа, рассмотрим задачу, которую я даю на уроках в теме «Закон Ома для полной цепи».
Задача №1. Записать закон Ома для цепи, изображенной на рисунке
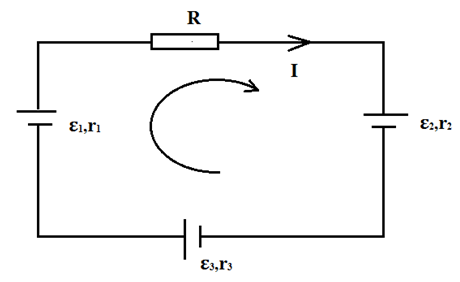
Решение: Вначале покажем направление тока. Это делается произвольно, но я принял во внимание то, что ток в цепи направлен от «+» к «-». Так же произвольно выбираем направление положительного обхода (выбрано по часовой стрелке). Стоит помнить – если направление тока совпадает с направлением положительного обхода, тогда ток берем со знаком «+», в противном случае со знаком «-». Цепь содержит четыре последовательно соединенных сопротивления, следовательно, общее сопротивление цепи равно их сумме. Значение ЭДС источника берем с тем знаком, на какую клемму в источнике переходим, двигаясь по направлению положительного обхода. Так, например, в первом источнике, двигаясь по направлению обхода переходим с «-» на «+», значит ε1 берем со знаком «+», аналогично ε2 со знаком «-», ε3 со знаком «+». Таким образом ток в цепи равен:
![]()
Рассмотрим некоторые понятия
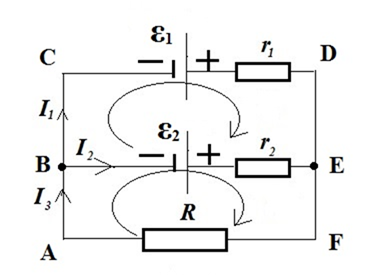
Узел – место
соединения трех и более ветвей или проводов. На рисунке всего два узла B
и
E, но они равноправные, т. е. связывают
одни и те же токи, поэтому рассматривать при решении можно любой из них.
Ветвь – участок электрической цепи между двумя узлами, по которому
протекает один и тот же ток. На рисунке присутствуют три различных ветви B-C-D-E,
B-E
и
B-A-F-E.
Замкнутый контур – любой замкнутый путь электрической цепи,
проходящий по нескольким ветвям
Перейдем теперь непосредственно к законам:
1.Для произвольного узла алгебраическая сумма токов ровна нулю. При этом токи, входящие в узел, берем со знаком «+», выходящие со знаком «-». Можно сказать, и по-другому – сумма токов, входящих в узел равна сумме токов, выходящих из узла. Ну здесь кому как нравиться, суть от этого не изменится.
2. Для произвольного контура алгебраическая сумма падений напряжения на участках контура (I*R) равна алгебраической сумме ЭДС источников в контуре.
![]()
При решении задач поступаем так же, как и в задаче №1, рассмотренной выше. Произвольно расставляем направления токов, выбираем направления положительного обхода для каждого контура. Если при движении по направлению обхода совпадаем с током, то произведение IR берем со знаком «+», иначе со знаком «-». Если при движении по направлению обхода в источнике переходим с отрицательной клеммы на положительную, то соответствующую ЭДС со знаком «+», иначе со знаком «-».
Рассмотрим применение данных законов на конкретных задачах.
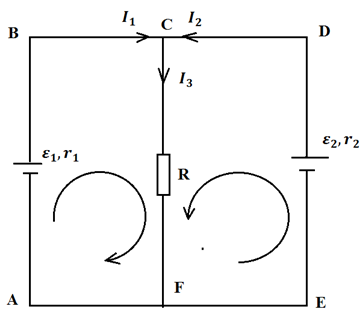
Задача1. Два источника с э. д. с. 1,2 и 1,5 В и внутренними сопротивлениями 0,3 и 0,5 Ом параллельно питают активное сопротивление 2 Ом. Определить токи в ветвях электрической цепи.
![]()
![]() Дано:
Решение:
Дано:
Решение:
![]()
![]()
![]()
![]()
![]()
![]()
Расставив направление токов и выбрав направления положительных обходов в каждом контуре, применим законы Кирхгофа
Для узла В: I1+I2-I3=0 (1)
Для контура ABEFA: I3R+I1r1=ε1 (2)
Для контура EDCFE: I2r2+I3R=ε2 (3)
Получили три уравнения с тремя неизвестными. Решим их как систему. Из уравнения (2) следует:
![]() (4)
(4)
Из уравнения (3) следует:
![]() (5)
(5)
Подставляя (4) и(5) в уравнение (1) получим:
![]()
После преобразований:
![]()
![]()
![]()
Тогда из уравнения (4) следует:
![]()
Из уравнения (5) следует:
![]()
Ответ: 0;0,6А;0,6А.
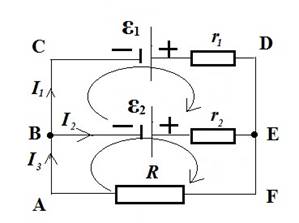
Задача 2. Даны две батареи
аккумуляторов с ЭДС ![]() с внутренним
сопротивлением
с внутренним
сопротивлением ![]() ,
, ![]() Реостат имеет
сопротивление
Реостат имеет
сопротивление ![]() Элементы цепи соединены
по схеме, показанной на рисунке. Найти силу тока в батареях и реостате.
Элементы цепи соединены
по схеме, показанной на рисунке. Найти силу тока в батареях и реостате.
![]() Дано:
Решение:
Дано:
Решение:
![]()
![]()
![]()
![]()
![]()
![]()
Расставив направление токов и выбрав направления положительных обходов в каждом контуре, применим законы Кирхгофа.
Для узла В: I3-I1-I2=0 (1)
Для контура ABEFA: I3R+I2r2=ε2 (2)
Для контура BCDEB: I1r1-I2r2=ε1-ε2 (3)
Получили три уравнения с тремя неизвестными. Решим их как систему. Из уравнения (2) следует:
![]() (4)
(4)
Из уравнения (3) следует:
![]() (5)
(5)
Подставляя (4) и(5) в уравнение (1) получим:
![]()
После преобразований:
![]()
![]()
![]()
Тогда из уравнения (4) следует:
![]()
Из уравнения (5) следует:
![]()
Ответ: 1А;0,5А;1,5А.
ЗАКЛЮЧЕНИЕ.
(по материалам методических рекомендаций при подготовке к
олимпиаде «РОСАТОМ»)
Так как же решают задачи (в том числе и олимпиадные) по физике и как лучше готовиться к олимпиадам? Чтобы научиться решать задачи, их нужно … решать. Пробовать, сомневаться, еще раз пробовать. Еще и еще пытаться «прочувствовать» логику физических законов и математических теорем, и снова пробовать решать задачи. Все же остальные советы по решениям являются конкретными и касаются тех разделов физики, которые рассматриваются в данной задаче. Тем не менее, несколько общих рекомендаций по решению задач (и, соответственно, подготовке к участию в олимпиадах) можно сформулировать. При решении задач полезно придерживаться определенного порядка действий.
1. Внимательно прочтите условие. Перескажите его себе «своими словами» и «своими же словами» сформулируйте вопрос задачи. Если вам это поможет, выпишите все данные задачи (слева, справа, снизу или сверху – не важно).
2. Начертите чертеж, причем постарайтесь сделать это в правильном масштабе: на чертеже кубы должны быть похожи на кубы, круги на круги, наклонные плоскости на наклонные плоскости. «Функционально» хороший чертеж поможет решить задачу, плохой – помешает. На чертеже приведите все данные условия, чтобы они были у вас «перед глазами».
3. Постарайтесь использовать численные значения физических величин в Международной системе единиц (СИ), хотя это и необязательно, особенно если ответ выражается через отношение однородных величин.
4. И теперь главное. Вспомните те определения, теоремы и законы, которые «управляют» рассматриваемой задачей или явлением, вспомните их логику, принципы, идеи, похожие случаи.
5. И ничего не выдумывайте. Все выдумали до нас! Поэтому если вы пытаетесь «выдумать» решение, то, скорее всего, вы действуете неправильно. Ваша задача не выдумать, а вспомнить! Вспомнить логику математических теорем и физических законов и точно «приспособить» их к рассматриваемому случаю. Но приспособить
нужно будет не формулу, а ту логику, которая в теоремах и законах содержится, и точно ей следовать.
6. Постарайтесь решить полученные на основе математических теорем и физических законов уравнения в общем («буквенном») виде, поскольку в этом случае проще проверить ответ, проверить размерность, частные случаи и т.д.
7. Проверьте размерность ответа. Единицы его измерения должны совпадать с единицей измерения искомой величины. Это означает, что если вы должны вычислить скорость, то ответ должен иметь размерность м/с, км/с, км/ч, но никак не метры, килограммы и т.д. Помните, что складывать или сравнивать величины разной размерности нельзя, и если в ответ у вас входит комбинация a +m, где a – ускорение тела, а m – его масса, то этот ответ неправильный.
8. Проверьте свой ответ на здравый смысл: если масса получилась отрицательной, скорость – больше скорости света, а ответ при каких-то возможных значениях параметров содержит нуль в знаменателе – ваш ответ неверен.
9. Попробуйте проверить ответ на частные случаи, т.е. рассмотрите такие модификации задачи, когда ответ понятен и без решения, и убедитесь, что полученный вами ответ в него переходит. Конечно, умение решать задачи приходит с опытом и изученными книгами.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.