
Сокращение
дробей, содержащих
квадратные корни, и освобождение
от иррациональности в знаменателе дроби
Цели: продолжить формирование умения преобразовывать выражения, содержащие квадратные корни.
Ход урока
I. Организационный момент.
II. Устная работа.
– Приведите подобные радикалы:
а) ![]() ; д)
; д)
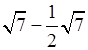 ;
;
б) 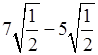 ; е)
; е)
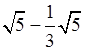 ;
;
в) ![]() ; ж)
; ж)
![]() ;
;
г) ![]() ; з)
; з)
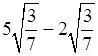 .
.
III. Формирование умений и навыков.
З а д а н и я, выполняемые учащимися на этом уроке, можно разбить на д в е г р у п п ы:
1) Сокращение дробей, содержащих квадратные корни.
2) Освобождение от иррациональности в знаменателе дроби.
1-я г р у п п а.
1. № 427, № 428.
2. № 429.
2-я г р у п п а.
1. № 431.
2. № 433 (а, в, д).
Р е ш е н и е
а) 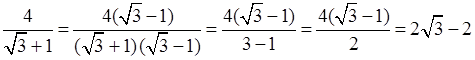 ;
;
в) 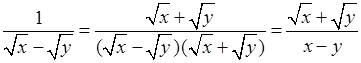 ;
;
д) 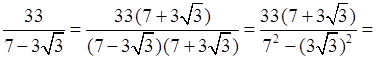
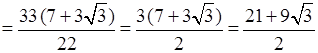 .
.
В классе с высоким уровнем подготовки можно дополнительно выполнить ещё несколько заданий.
1. Сократите дробь:
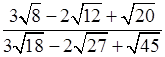 .
.
Р е ш е н и е
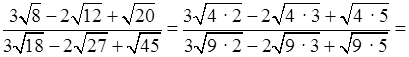
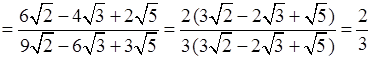 .
.
2. Вычислите:
![]() .
.
Р е ш е н и е
![]()
![]()
![]()
![]() .
.
3. Освободить от иррациональности в знаменателе дроби:
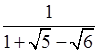 .
.
Р е ш е н и е
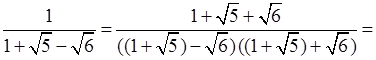
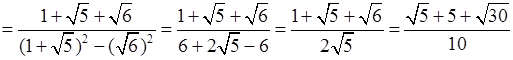 .
.
IV. Проверочная работа.
В а р и а н т 1
1. Упростите выражение:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
2. Выполните действия:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
3. Сократите дробь:
а) 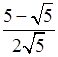 ; б)
; б)
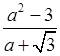 .
.
4. Освободитесь от иррациональности в знаменателе дроби:
а) ![]() ; б)
; б)
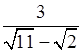 .
.
В а р и а н т 2
1. Упростите выражение:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
2. Выполните действия:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
3. Сократите дробь:
а) 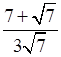 ; б)
; б)
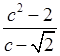 .
.
4. Освободить от иррациональности в знаменателе дроби:
а) ![]() ; б)
; б)
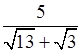 .
.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Как приводить подобные радикалы?
– Как освобождаться от иррациональности в знаменателе дроби в различных случаях?
Домашнее задание: № 430, № 432, № 433 (б, г, е).
Д о п о л н и т е л ь н о: № 503 (а, д), № 507 (а).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.