СОСТАВЛЕНИЕ СИСТЕМЫ УРАВНЕНИЙ

Составление системы уравнений
по условию задачи

Цели: изучить способ решения задач с помощью составления систем уравнений; формировать умение составлять системы уравнений по условию задачи и решать их.

Ход урока

I. Устная работа.

Какое из уравнений нужно записать в систему 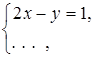 чтобы она имела единственное решение? не имела решений? имела бесконечное множество решений?

а) y + 3x = 7;                             в) y – 2x = 3;

б) 4x – 2y = 2;                           г) x = 5.

II. Объяснение нового материала.

Сначала следует вспомнить, в чём заключается способ решения задач с помощью составления уравнения, а затем показать, что задачи могут решаться и с помощью составления системы уравнений.

Разобрав примеры решения задач, учащиеся должны сформулировать действия, которые необходимо выполнить, чтобы решить задачу с помощью составления системы уравнений.

III. Формирование умений и навыков.

Сначала необходимо дать учащимся несколько заданий на составление системы уравнений по условию задачи, а затем уже переходить непосредственно к решению задач.

1. Запишите с помощью системы уравнений следующую ситуацию:

а) Сумма двух чисел равна 17. Одно из них на 7 меньше другого.

б) Периметр прямоугольника равен 400 м. Его длина в 3 раза больше ширины.

в) Четыре боксёра тяжёлого веса и пять боксёров лёгкого веса вместе весят 730 кг. Спортсмен тяжелого веса весит на 70 кг больше спортсмена лёгкого веса.

г) Таня заплатила за 3 тетради и 2 карандаша 58 р., а Лена за 3 такие же тетради и 1 карандаш – 78 р.

2. № 1099, № 1101.

3. № 1103.

4. № 1104.

Решение:

Пусть ослица несла х мешков, а мул нёс у мешков. Если ослица отдаст 1 мешок мулу, то у неё останется х – 1 мешок, а у мула станет у + 1 мешок. По условию у мула станет в 2 раза больше мешков, чем у ослицы, то есть получим уравнение: у + 1 = 2(х – 1).

Если мул отдаст 1 мешок ослице, то у него останется у – 1 мешок, а у ослицы станет х + 1 мешок. По условию в этом случае количество мешков у них станет равным, то есть получим уравнение: у – 1 = х + 1.

В итоге имеем систему уравнений:

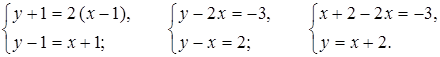
x + 2 – 2x = –3;

–х = –5;

х = 5;

у = 5 + 2;

у = 7.

Ответ: 5 и 7 мешков.

IV. Итоги урока.

– Какие существуют способы решений систем уравнений с двумя переменными? Опишите каждый из них.

– Как решаются задачи с помощью составления системы уравнений?

– Придумайте ситуацию, которая описывается следующей системой уравнений: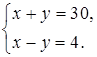

Домашнее задание: № 1100, № 1102, № 1105.