Совместимые и несовместимые величины

Համատեղելի և անհամատեղելի մեծույուններ

Մեզ արդեն հայտնի է, որ մակրոաշխարհից միկրոաշխարհին անցնելիս կոորդինատն ու համապատասխան կանոնիկ համալուծ իմպուլսը չեն  կարող միաժամանակ ունենալ կատարյալ որոշակի արժեքներ: Եթե տված վիճակում մասնիկի  կոորդինատն ունի անորոշություն, ապա համապատասխան  իմպուլսը կունենա 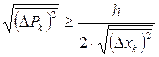 անորոշությունը: Այս աիրադրությունը յուրահատուկ չէ միայն կոորդինատներին ու իմպուլսներին. Քանի որ մնացած բոլոր դասական ֆիզիկական մեծությունները ֆունկցիա են կոորդինատներից և իմպուլսներից, ապա հասկանալի է, որ նրանք նույնպես կունենան որոշ անորոշություններ: Այսինքն՝ բացի կոորդինատներից ու կանոնիկ համալուծ իմպուլսներից մյուս ֆիզիկական մեծությունների մեջ էլ կան այնպիսիները, որոնք միկրոաշխարհում չեն կարող միաժամանակ ցանկացած ճշտությամբ չափելու հարցը դառնում է անօմաստ: Հետագայում, միաժամանակ որոշակի արժեքներ ունեցող ֆիզիկական մեծությունները կանվանենք համատեղելի, իսկ նրանց, որոնց միաժամանակ չեն կարող ունենալ որոշակի արժեքներ՝ անհամատեղելի մեծություններ:

Համատեղելի ու անհամատեղելի մեծությունների համար գոյություն ունեն հետևյալ թեորեմները. Կոմուտատիվ օպերատորներին համապատասխանում են համատեղելի մեծություններ և հակառակը, համատեղելի մեծություններին համապատասխանում են կոմուտատիվ օպերատորներ:

Դիցուք տված են երկու  և  կոմուտատիվ օպերատորներ.

,                                                               (1)

և հայտնի են -ի սեփական արժեքներն ու սեփական ֆունկցիաները.

:                                                       (2)

Ենթադրենք, որ f-ի սպեկտորը դիսկրետ է, բայց ներքոհիշյալ ապացույցը կարելի է նույնությամբ գրել նաև անընդհատ սպեկտորի դեպքի համար: (1) և (2) հավասարումներից ունենք.

                                                      (3)

Այստեղից երևում է, որ -ը նույնես հանդիսանում է  օպերատորի սեփական  ֆունկցիան  սեփական արժեքի համար: Եթե -ի սեփական արժեքները այլասերված չեն, այսինքն, եթե  սեփական արժեքին համապատասխանում է միայն մի սեփական ֆունկցիա, ապա հասկանալի է, որ  և  ֆունկցիաները հաստատունի ճշտությամբ պետք է համընկնեն իրար հե.

                                                                 (4)

Որտեղ -ը այն հաստատունն է, որով իրարից տարբերվում են  և  ֆունկցիաները: Բայց (4)-ը հանդիսանում է սեփական արժեքների ու սեփական ֆունկցիաների դիֆերենցիալ հավասարումը  ֆիզիկական մեծության համար: Նա ցույց է տալիս, որ -ը միաժամանակ  օպերատորի սեփական ֆունկցիան է  սեփական արժեքի համար: Այսպիսով, մի ընդհանուր  վիճակում միաժամանակ որոշակի արժեքներ ունեն -ը և -ն:

Այժմ ապացուցենք հակադարձ թեորեմը: Դիցուք -ը և -ն համատեղելի մեծություններ են և  վիճակում նրանք ունեն որոշակի  ու  արժեքներ.

,                                                         (5)

Ապացուցենք, որ  և  օպերատորները կոմուտատիվ են: Առաջին հավասարման վրա ազդենք -ով, երկրորդի վրա՝ -ով, և իրարաից հանենք, կստանանք՝

                                                         (6)

Սակայն (6)-ը դեռ չի նշանակում, որ , որովհետև -ն կամայական ֆունկցիա չէ: Դիցուք -ն կամայական վիճակի ալիքային ֆունկցիա է, այն վերլուծենք շարքի ըստ  սեփական ֆունկցիաների.

                                                                   (7)

(6)-ից և (7)-ից հետևում է, որ

                                 (8)

Այսպիսով, կամայական  ֆունկցիայի համար , սա նշանակում է, որ  և  օպերատորները կոմուտատիվ են.

                                                                      (9)

Այս թեորեմները ճիշտ են նաև այլասերված սեփական արժեքների դեպքի համար, բայց դրանց ապացույցները այստեղ չենք բերի: Անհամատեղելի մեծությունների համար գոյություն ունի անորոշությունների առնչություն.

:                                            (10)

Եթե  և , ապա հարցին կարելի է մոտենալ դասականորեն, այսինքն՝ կարելի է խոսել -ի և -ի միաժամանակյա չափման մասին: Իսկ եթե  և , ապա դասական մոտեցումը սխալ է: Վերջին դեպքում իմաստ ունի խոսել միայն նրանցից մեկնումեկի ճշգրիտ արժեքների մասին, որոնք կորոշվեն սեփական արժեքների և սեփական ֆունկցիաների դիֆերենցիալ հավասարումից:

Շրեդինգերի հավասարումը

Ինչպես դասական ֆիզիկայում, այնպես էլ քվանտային մեխանիկայում, երբ  ուժական դաշտը, որում գտնվում է համակարգը, կախված չէ ժամանակից, կարող ենք խոսել էներգիայի մասին որն այդպիսի պայմանում ժամանակի ընթացքում ունի իր արժեքը պահպանելու հատկություն: Սակայն, քվանտային դեպքում, բացի այն, որ էներգիան կարող է ունենալ դիսկրետ արժեքներ, գոյություն ունի մի էական տարբերություն ևս: Դասական ֆիզիկայում էներգիան կարելի է բաժանել կինետիկ և պոտենցիալ մասերի և չափել առանձին-առանձին: Քվանտային դեպքում այդ տիպի բաժանումը և հետևաբար կինետիկ ու պոտենցիալ էներգիաների միաժամանակյա չափումը դառնում են անիմաստ, որովհեռև նրանք անհամատեղելի մեծություններ են: Ասածից չի հետևում, որ լրիվ էներգիան արժեքազրկվում է, ընդհակառակը, նա ատոմական աշխարկում ամենակարևոր ֆիզիկական մեծությունն է, սակայն անիմաստ է նրան կինետիկ ու պոտենցիալ մասերի բաժանելը: Լրիվ էներգիան քվանտային դեպքում կարող է ունենալ որոշակի արժեքներ և այն պետք է չափել որպես ամբողջություն՝ առանց մասերի բաժանելու: Ինչպես բոլոր ֆիզիկական մեծությունները, այնպես էլ էներգիայի արժեքները պետք է որոշվեն սեփական արժեքների և սեփական ֆունկցիաների դիֆերենցիալ հավասարումից, որը տվյալ դեպքում կգրվի այսպես.

,                                                     (1)

Որտեղ -ը էներգիայի օպերատորն է: Այս հավասարումը կրում է Շրեդինգերի անունը:

-ը կառուցվում է ընդհանուր կանոնով: օպերատորը ստանալու համար պետք է իմպուլսներով արտահայտված էներգիայի դասական արտահայտության (այլ կերպ ասած Համիլտոնի ֆունկցիայի) մեջ իմպուլսները փոխարինել  ածանցման գործողություններով: Քններնք այն դեպքը, երբ պոտենցիալ էներգիան կախված չէ արագությունից: Այդ դեպքում կոորդինատների դեկարտյան համակարգում կինետիկ էներգիան կախված է միայն իմպուլսներից, իսկ պոտենցիալ էներգիան՝ միայն կոորդինատներից՝ , և հետևաբար էներգիայի օպերատորի համար կունենանք.

                                      (2)

Հիշենք, որայստեղ -ով նշանակված է բոլոր կոորդինատների համախմբությունը: (2)-ը կոչվում է Համիլտոնի օպերատոր:

Կինետիկ էներգիան քառակուսային ֆունկցիա է իմպուլսներից: Դա նշանակում է, որ Համիլտոնի (2) օպերատորը երկրորդ կարգի բարդ ածանցման գործողություն է: Հետևաբար Շրեդինգերի (1) հավասարումը հանդիսանում է երկրորդ կարգի մասնական ածանցյալներով դիֆերենցիալ հավասարում, որը լուծում են ընդհանուր եղանակով: Սկզբում (1) դիֆերենցիալ հավասարումները լուծում են մաթեմատիկայում գոյություն ունեցող մեթոդներով: Այդ լուծումը որպես պարամետր պարունակում է էներգիա՝ E, այնուհետև E-ն ընտրում են այնպես, որ լուծումները բավարարեն ստանդարտ պայմաններին: Կարող է պատահել երկու դեպք. 1) երբ ստանդարտ պայմաններին բավարարող  լուծումները ստացվում են E-ի դիսկրետ արժեքների դեպքում, 2) երբ ստանդարտ պայմաններին բավարարող լուծումները ստացվում են E-ի անընդհատ արժեքների համար: E-ի այդ արժեքները (որոնց համար ստացվում են ստանդարտ պայմաններին բավարարող լուծումներ) իրենցից ներկայացնում են հենց ուսումնասիրվող համակարգի էներգիայի հնարավոր արժեքները:

Մանրամասն քննարկենք մի մասնիկի դոպքը: Համիլտոնի ֆունկցիան հավասար է՝

:

Այստեղ , , -ը փոխարինենք

,               ,              

Օպերատորներով, կստանանք Համիլտոնի օպերատորը.

,                                             (3)

Որտեղ

                                                 (4)

Լապլասի օպերատորն է: (3)-ը տեղադրելով  (1)-ի մեջ կստանանք.

                                    (5)

Գրության հարմարության համար բաց թողեցինք ալիքային ֆունկցիայի E ինդեքսը: Սա իրենից ներկայացնում է Շրեդինգերի հավասարումը մի մասնիկի համար: Հետագայում մենք ցույց կտանք, որ երբ E<U₀, որտեղ U₀-ն պոտենցիալ էներգիայի արժեքն է անվերջ հեռու կետում, ապա էներգիայի սպեկտրը կլինի դիսկրետ, իսկ E> U₀ դեպքում այն կլինի անընդհատ:

Դասական մեխանիկայում Համիլտոնի ֆունկցիան ունի ավելի ընդարձակ իմաստ, քան էներգիան: Իրոք, մասնավոր դեպքում, երբ ուժական դաշտը կախված չէ ժամանակից, այն համընկնում է էներգիայի հետ և, բացի այդ, բոլոր դեպքերում, անկախ այն բանից համակարգի էներգիան պահպանվում է, թե ոչ, սկզբնական պայմանների հետ միասին որոշում է համակարգի վիճակը (հիշենք Համիլտոնի կանոնիկ հավասարումները) ժամանակի ցանկացած պահին: Նման դրություն գոյություն ունի նաև քվանտային մեխանիկայում, այսինքն՝ կարելի է խոսել Համիլտոնի օպերատորի մասին այն դեպքում ևս, երբ ուժական դաշտը կախված է ժամանակից.

                                                          (6)

Մենք դեռ կտեսնենք, որ Համիլտոնի օպերատորով է որոշվում վիճակի փոփոխությունը ժամանակի ընթացքում, այսինքն՝ շարժման քվանտային հավասարումները: Մասնավոր դեպքում, երբ U(q) ուժական ֆունկցիան ժամանակի ընթացքում մնում է անփոփոխ (6)-ը համընկնում է (2)-ի հետ, այսինքն՝ հանդիսանում է էներգիայի օպերատորը:

Այժմ քննարկենք էլեկտրամագնիսական դաշտում գտնվող լիցքավորված մասնիկի դեպքը: Ինչպես հայտնի է ոչ ռելյատիվիստական շարժման ժամանակ, էլեկտրամագնիսական դաշտում գտնվող e լիցք ունեցող մասնիկի Համիլտոնի ֆունկցիան ունի հետևյալ տեսքը.

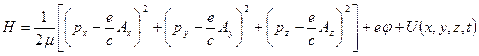            (7)

Այստեղ -ն և -ն էլեկտրամագնիսական դաշտի սկալյար ու վեկտորական պոտենցիալներն են, որոնք E և H լարվածությունների հետ կապած են

H=rot A;                                                            (8)

Առնչություններով: Բացի այդ, նրանք բավարարում են Լորենցի առնչությանը.

                                                                     (9)

(8) և (9) առնչություններով  և A պոտենցիալները չեն որոշվում միարժեք ձևով, այլ հայտնի են, այսպես կոչված, գրադիենտային ձևափոխության ճշտությամբ: (6)-ու U(x,y,z,t)-ն այլ բնույթի ուժական դաշտ է, իսկ  p_x, p_y, p_z-ը x, y և z կոորդինատներին համապատասխանող ընդհանրացրած իմպուլսներն են: Նրանք կապված են սովորական  իմպուլսի հետ

                                                              (10)

Առնչությամբ:

Մասնիկի Համիլտոնի օպերատորը գտնելու համար պետք է (7)-ում ըստ արդեն հաստատված ընդհանուր կանոնի x, y,  z կոորդինատներին համապատասխանող p_x, p_y և p_z կանոնիկ համալուծ  իմպուլսները (և ոչ-ի պրոյեկցիաները, որոնք կանոնիկ համալուծ չեն կոորդինատների հետ, հիշենք որ ) փոխարինենք

;               ;                                            (11)

օպերատորներով: Կստանանք.

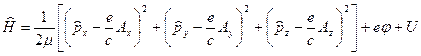               (12)

Օգտվելով օպերատորական հանրահաշվի օրենքներից (12)-ը բերենք կիրառությունների համար հարմար տեսքի.

:

Այստեղից հաշվի առնելով, որ

,

Կստանանք

:

Նման ձևափոխություններ կստանանք (12)-ի միջակ փակագծերում գտնվող մյուս երկու անդամների հետ և ստացած արտահայտությունները գումարենք.

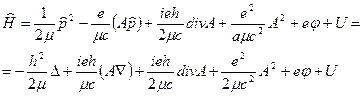                 (13)

Ճառագայթման դաշտի դեպքում կարելի է ընտրել , հետևաբար, (9) առնչության շնորհիվ diva=0 և Համիլտոնի օպերատորի համար կունենանք:

                             (14)

Ստացիոնար դաշտերի դեպքում, երբ     -ն, -ն և -ն կախված չեն ժամանակից, Համիլտոնի (13) օպերատորը նույնպես ժամանակից անկախ է: Այս դեպքում մենք կարող ենք գրել Շրեդինգերի  հավասարումը և խոսել էներգիայի սեփական արժեքների ու սեփական ֆունկցիաների մասին:

Համիլտոնի օպերատորը երբեմն անհրաժեշտ է լինում գրել կորագիծ կոորդինատներով (սֆերիկ, պարաբոլիկ և այլն), դրա համար պետք է (3)-ում Լապլասի  օպերատորը ներկայացնել համապատասխան կոորդինատներով: