
способ подстановки
Цели: закрепить умение учащихся решать системы линейных уравнений способом подстановки; проверить уровень усвоения материала.
Ход урока
I. Устная работа.
1. Является ли пара чисел (–2; –2) решением системы уравнений:
а) 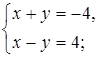 б)
б) 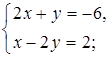 в)
в) 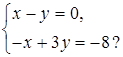
2. Из какого уравнения системы и какую переменную выразить «удобнее»? Ответ объясните.
а) 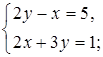 б)
б) 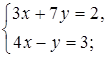 в)
в) 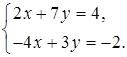
II. Формирование умений и навыков.
1. № 1075.
2. № 1171 (а).
Решение:
![]()
![]()
2 (1 – 2у) + 1 = –3у;
2 – 4у + 1 = –3у;
–у = –3;
у = 3;
х = 1 – 2у;
х = 1 – 2 · 3 = –5.
Ответ: (–5; 3).
3. № 1077.
Решение:
а) 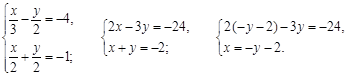
2 (–у – 2) – 3у = –24;
–2у – 4 – 3у = –24;
–5у = –20;
у = 4;
х = –у – 2;
х = – 4 – 2 = –6.
Ответ: (–6; 4).
Замечание. Обращаем внимание на опечатку: во втором уравнении системы вместо –2 должно стоять –1.
в) 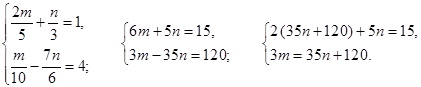
2 (35п + 120) + 5п = 15;
70п + 240 + 5п = 15;
75п = –225;
п = –3;
3т = 35 · (–3) + 120;
3т = –105 + 120 = 15;
т = 5.
Ответ: т = 5, п = –3.
4*. № 1173.
Решение:
а) 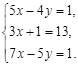
Система содержит три уравнения, а переменных всего две. Такая система имеет решение, если общее решение двух любых её уравнений будет являться решением третьего уравнения.
Сначала нужно решить систему из двух уравнений:
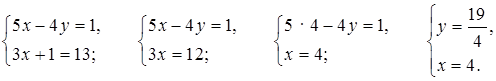
Подставим
пару чисел 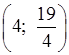 в третье уравнение:
в третье уравнение:
7 · 4
– 5 · ![]() = 1.
= 1.
Очевидно, что равенство будет неверным. Поэтому исходная система решений не имеет.
б) 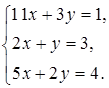
Решим систему уравнений:
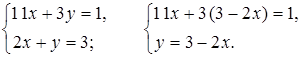
11х + 3(3 – 2х) = 1;
11х + 9 – 6х = 1;
5х = –8;
х = –1,6;
у = 3 – 2 · (–1,6);
у = 6,2.
Подставим пару чисел (–1,6; 6,2) в третье уравнение:
5 · (–1,6) + 2 · 6,2 = 4;
–8 + 12,4 = 4;
4,4 = 4 – неверно.
Значит, исходная система решений не имеет.
III. Проверочная работа.
Вариант 1
1. Решите систему уравнений 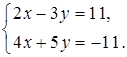
2. Не выполняя построений, найдите координаты точки пересечения графиков уравнений 3x + 7y = 2 и 2x – 5y = 1.
3. Решите систему уравнений 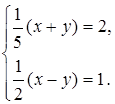
Вариант 2
1. Решите систему уравнений 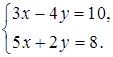
2. Не выполняя построений, найдите координаты точки пересечения графиков уравнений 2x – 9y = 1 и 5x + 2y = 3.
3. Решите систему уравнений 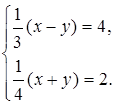
IV. Итоги урока.
Домашнее задание: № 1076; № 1171 (б); № 1078.
Дополнительно: № 1174.
Вариант 1
1. Решите систему
уравнений ![]()
2. Не выполняя построений, найдите координаты точки пересечения графиков уравнений 3x + 7y = 2 и 2x – 5y = 1.
3. Решите систему
уравнений 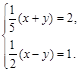
Вариант 2
1. Решите систему
уравнений 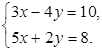
2. Не выполняя построений, найдите координаты точки пересечения графиков уравнений 2x – 9y = 1 и 5x + 2y = 3.
3. Решите систему
уравнений 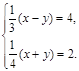
Вариант 1
1. Решите систему
уравнений ![]()
2. Не выполняя построений, найдите координаты точки пересечения графиков уравнений 3x + 7y = 2 и 2x – 5y = 1.
3. Решите систему
уравнений 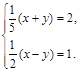
Вариант 2
1. Решите систему
уравнений 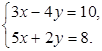
2. Не выполняя построений, найдите координаты точки пересечения графиков уравнений 2x – 9y = 1 и 5x + 2y = 3.
3. Решите систему
уравнений 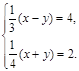
Вариант 1
1. Решите систему
уравнений ![]()
2. Не выполняя построений, найдите координаты точки пересечения графиков уравнений 3x + 7y = 2 и 2x – 5y = 1.
3. Решите систему
уравнений 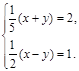
Вариант 2
1. Решите систему
уравнений 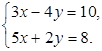
2. Не выполняя построений, найдите координаты точки пересечения графиков уравнений 2x – 9y = 1 и 5x + 2y = 3.
3. Решите систему
уравнений 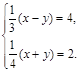
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.