
способ сложения
Цели: закрепить умение учащихся решать системы уравнений способом сложения; разобрать, как с помощью системы уравнений можно составить уравнение прямой, проходящей через две заданные точки; проверить уровень усвоения материала.
Ход урока
I. Устная работа.
1. Являются ли следующие системы уравнений равносильными:
а) 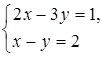 и
и 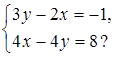 б)
б) 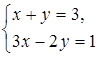 и
и 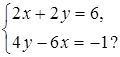
2. Первое уравнение системы у = 2х – 1. Подберите второе уравнение так, чтобы полученная система:
а) имела единственное решение;
б) не имела решений;
в) имела бесконечное множество решений.
II. Формирование умений и навыков.
1. № 1086 (а, в).
Решение:
а) 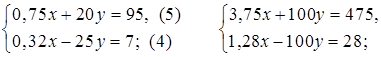
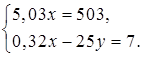
5,03х = 503;
х = 100;
0,32 · 100 – 25у = 7;
–25у = –25;
у = 1.
Ответ: (100; 1).
2. № 1092 (а).
2-я группа
1. № 1087 (а, в).
Решение:
а) Чтобы составить уравнение прямой, нужно найти коэффициенты k и b. Подставляя координаты данных точек M (5; 5) и N (–10; –19) в уравнение y = kx + b, получим систему уравнений:
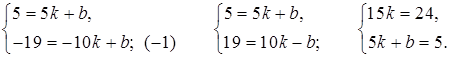
15k = 24;
k = 1,6;
5 · 1,6 + b = 5;
b = 5 – 8;
b = –3. Получим уравнение: у = 1,6х – 3.
2. № 1088.
3. № 1091.
Решение:
Чтобы задать формулой функцию по её графику, нужно найти на этом графике две любых точки и записать их координаты. Например, А (–1; 1) и В (1; –3). Задача свелась к составлению уравнения прямой y = kx + b, проходящей через точки А и В.
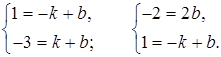
2b = –2;
b = –1;
1 = –k – 1;
k = –2.
Получим уравнение: у = –2х – 1.
Сильным учащимся можно предложить дополнительно выполнить задания на карточках.
Карточка 1
Решите систему уравнений:
а) 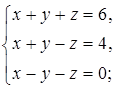 б)
б) 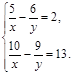
Решение заданий на карточке 1
а) 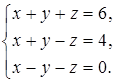
Если сложить первое и третье уравнения системы, то получится уравнение с одной переменной:
2х = 6;
х = 3.
Подставив найденное значение х в первое и второе уравнения, получим и решим систему:
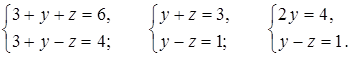
2у = 4;
у = 2;
2 – z = 1;
z = 1. Ответ: (3; 2; 1).
б) Сделаем замену переменных: ![]() = a,
= a, ![]() = b.
Получим и решим систему уравнений:
= b.
Получим и решим систему уравнений:
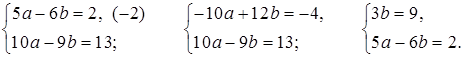
3b = 9;
b = 3;
5a – 6 · 3 = 2;
5a = 20;
a = 4.
Вернёмся к замене: ![]() = 4, значит, x =
= 4, значит, x = ![]() ;
; ![]() = 3,
значит, y =
= 3,
значит, y = ![]() . Ответ:
. Ответ:
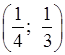 .
.
III. Проверочная работа.
Вариант 1 Решите систему уравнений.
а) 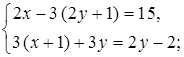 б)
б) 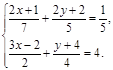
Вариант 2
Решите систему уравнений.
а) 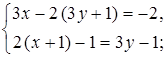 б)
б) 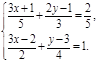
IV. Итоги урока.
Домашнее задание: № 1086 (б, г); № 1087 (б, г); № 1089; № 1092 (б).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.