СРАВНЕНИЕ ЗНАЧЕНИЙ ВЫРАЖЕНИЙ

Сравнение значений выражений

Цели: продолжить формировать умение сравнивать значения числовых выражений, а также выражений с переменными при заданных значениях входящих в них переменных; ввести понятие строгого и нестрогого неравенства; формировать умение составлять выражения по условию задачи и сравнивать их значения.

Ход урока

I. Организационный момент

Устная работа.

1. Сколько процентов составляет: а) число 8 от числа 200; б) число 15 от числа 1500; в) число 24 от числа 12; г) число  от ?

2. Замените звездочку знаком: >, < или =.

а)  * 3; г) 32,5 – 12 * 4,01; б)  * 5 – 2,5; д) (5 – 2) · 7,5 * 5 – 2 · 7,5;

в) (–2) ∙ 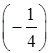  ∙  7 * – 3,5;                              е) –3,7 – 2,4 * –6,2.

3. Прочитайте неравенство:

а) 3,7 < 3,8 < 3,95; в) –b < –a < – c; б) k < p < 2k; г) .

II. Проверочная работа.

Вариант 1

1. Сравните значения выражений:

1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;

2) 2a – 3b и 3a – 2b при а = –2 и b = 3.

2. Запишите  в  виде  двойного  неравенства:  t  положительно  и  меньше 45.

Вариант 2

1. Сравните значения выражений:

1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;

2) 3a + 2b и 2a – 3b при а = –2 и b = 4.

2. Запишите в виде двойного неравенства: р отрицательно и больше –18.

III. Объяснение нового материала.

Вводится понятие строгого и нестрогого неравенства на конкретных примерах (число дней в месяце, количество пассажиров в автобусе, предельные температуры и т. п.).

Определение. Неравенства, составленные с помощью знаков > и <, называют строгими неравенствами, а неравенства, составленные с помощью знаков ≥ и ≤, называют нестрогими.

Необходимо подчеркнуть, что нестрогое неравенство является верным, если выполняется хотя бы одно соотношение:

18 ≥ 14 – верно (выполняется 18 > 14);

–35 ≤ –35 – верно (выполняется –35 = –35).

Если не выполняется ни одно из соотношений, то неравенство является неверным:

–35 ≥ –34.

Двойные  неравенства  также  могут  быть  записаны  с  помощью  знаков ≥ и ≤:

18 ≤ х ≤ 19;  1,7 < п ≤ 1,8;  .

IV. Формирование умений и навыков.

1. № 60 (устно); № 61 (устно).

2. Задание по вариантам.

Запишите каждое предложение с помощью знаков неравенства. Подберите три значения переменной, при которых данное неравенство верно, и три, при которых неверно.

Вариант 1

1) а) t меньше 5;

    б) р больше или равно –11,3;

    в) т – неотрицательное число;

2) а) х меньше 5 и больше или равно 4;

    б) а больше 0,01 и меньше 0,02;

    в) с больше или равно –0,7 и отрицательно.

Вариант 2

1) а) t больше 7;

    б) υ меньше или равно –1,17;

    в) р – неположительное число;

2) а) b меньше 8 и больше или равно –7;

    б) а меньше 0,07 и больше 0,06;

    в) q меньше или равно 0,1 и положительно.

3. Расположите числа в порядке возрастания.

.

4. Расположите числа в порядке убывания.

(0,3)²; 0,3; (0,3)³.

1. Один сплав состоит из 5 кг олова и 15 кг меди, другой – из 3 кг олова и 7 кг меди. В каком из сплавов процентное содержание меди больше?

При  решении  задач  на  проценты  нужно  использовать  наглядное изображение данных, что в дальнейшем позволит учащимся грамотно выполнять анализ условия текстовых задач, решаемых алгебраическим методом.

Решение:

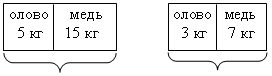
   20 кг                              10 кг

1) Масса первого сплава равна 20 кг, второго – 10 кг.

2) Выразим  процентное  содержание  меди  в  первом  и  во  втором сплавах:

 ∙  100 % = 75 %  и   ∙  100 % = 70 %.

3) 75 > 70,  значит,  в  первом  сплаве  процентное  содержание  меди больше.

Ответ: в первом сплаве.

2. № 65.

Решение:

Средняя скорость автомобиля «Жигули» равна  км/ч, а автомобиля «Москвич» –  км/ч. Сравним средние скорости автомобилей:

а) Если х = 12,5, у =10,5, то  = 56, а = 60. То есть при данных значениях переменных верно неравенство  < .

б) Если х = у = 14, то  = 50, а  = 45. То есть при данных значениях переменных верно неравенство  > .

Ответ: а) Средняя скорость автомобиля «Жигули» меньше. б) Средняя скорость автомобиля «Жигули» больше.

V. Итоги урока.

– Какое неравенство называется строгим? Приведите примеры.

– Какое неравенство называется нестрогим? Приведите примеры.

– Когда верно нестрогое неравенство? Когда оно не верно? Приведите примеры.

Домашнее задание: 1. № 62, № 63, № 64.

Вариант 1

1) а) t меньше 5;

    б) р больше или равно –11,3;

    в) т – неотрицательное число;

2) а) х меньше 5 и больше или равно 4;

    б) а больше 0,01 и меньше 0,02;

    в) с больше или равно –0,7 и отрицательно.

Вариант 2

1) а) t больше 7;

    б) υ меньше или равно –1,17;

    в) р – неположительное число;

2) а) b меньше 8 и больше или равно –7;

    б) а меньше 0,07 и больше 0,06;

    в) q меньше или равно 0,1 и положительно.

Вариант 1

1) а) t меньше 5;

    б) р больше или равно –11,3;

    в) т – неотрицательное число;

2) а) х меньше 5 и больше или равно 4;

    б) а больше 0,01 и меньше 0,02;

    в) с больше или равно –0,7 и отрицательно.

Вариант 2

1) а) t больше 7;

    б) υ меньше или равно –1,17;

    в) р – неположительное число;

2) а) b меньше 8 и больше или равно –7;

    б) а меньше 0,07 и больше 0,06;

    в) q меньше или равно 0,1 и положительно.

Вариант 1

1) а) t меньше 5;

    б) р больше или равно –11,3;

    в) т – неотрицательное число;

2) а) х меньше 5 и больше или равно 4;

    б) а больше 0,01 и меньше 0,02;

    в) с больше или равно –0,7 и отрицательно.

Вариант 2

1) а) t больше 7;

    б) υ меньше или равно –1,17;

    в) р – неположительное число;

2) а) b меньше 8 и больше или равно –7;

    б) а меньше 0,07 и больше 0,06;

    в) q меньше или равно 0,1 и положительно.

Вариант 1

1) а) t меньше 5;

    б) р больше или равно –11,3;

    в) т – неотрицательное число;

2) а) х меньше 5 и больше или равно 4;

    б) а больше 0,01 и меньше 0,02;

    в) с больше или равно –0,7 и отрицательно.

Вариант 2

1) а) t больше 7;

    б) υ меньше или равно –1,17;

    в) р – неположительное число;

2) а) b меньше 8 и больше или равно –7;

    б) а меньше 0,07 и больше 0,06;

    в) q меньше или равно 0,1 и положительно.

Вариант 1

1) а) t меньше 5;

    б) р больше или равно –11,3;

    в) т – неотрицательное число;

2) а) х меньше 5 и больше или равно 4;

    б) а больше 0,01 и меньше 0,02;

    в) с больше или равно –0,7 и отрицательно.

Вариант 2

1) а) t больше 7;

    б) υ меньше или равно –1,17;

    в) р – неположительное число;

2) а) b меньше 8 и больше или равно –7;

    б) а меньше 0,07 и больше 0,06;

    в) q меньше или равно 0,1 и положительно.

Вариант 1

1) а) t меньше 5;

    б) р больше или равно –11,3;

    в) т – неотрицательное число;

2) а) х меньше 5 и больше или равно 4;

    б) а больше 0,01 и меньше 0,02;

    в) с больше или равно –0,7 и отрицательно.

Вариант 2

1) а) t больше 7;

    б) υ меньше или равно –1,17;

    в) р – неположительное число;

2) а) b меньше 8 и больше или равно –7;

    б) а меньше 0,07 и больше 0,06;

    в) q меньше или равно 0,1 и положительно.

Вариант 1

1. Сравните значения выражений:

1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;

2) 2a – 3b и 3a – 2b при а = –2 и b = 3.

2. Запишите  в  виде  двойного  неравенства:  t  положительно  и  меньше 45.

Вариант 2

1. Сравните значения выражений:

1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;

2) 3a + 2b и 2a – 3b при а = –2 и b = 4.

2. Запишите в виде двойного неравенства: р отрицательно и больше –18.

Вариант 1

1. Сравните значения выражений:

1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;

2) 2a – 3b и 3a – 2b при а = –2 и b = 3.

2. Запишите  в  виде  двойного  неравенства:  t  положительно  и  меньше 45.

Вариант 2

1. Сравните значения выражений:

1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;

2) 3a + 2b и 2a – 3b при а = –2 и b = 4.

2. Запишите в виде двойного неравенства: р отрицательно и больше –18.

Вариант 1

1. Сравните значения выражений:

1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;

2) 2a – 3b и 3a – 2b при а = –2 и b = 3.

2. Запишите  в  виде  двойного  неравенства:  t  положительно  и  меньше 45.

Вариант 2

1. Сравните значения выражений:

1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;

2) 3a + 2b и 2a – 3b при а = –2 и b = 4.

2. Запишите в виде двойного неравенства: р отрицательно и больше –18.

Вариант 1

1. Сравните значения выражений:

1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;

2) 2a – 3b и 3a – 2b при а = –2 и b = 3.

2. Запишите  в  виде  двойного  неравенства:  t  положительно  и  меньше 45.

Вариант 2

1. Сравните значения выражений:

1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;

2) 3a + 2b и 2a – 3b при а = –2 и b = 4.

2. Запишите в виде двойного неравенства: р отрицательно и больше –18.

Вариант 1

1. Сравните значения выражений:

1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;

2) 2a – 3b и 3a – 2b при а = –2 и b = 3.

2. Запишите  в  виде  двойного  неравенства:  t  положительно  и  меньше 45.

Вариант 2

1. Сравните значения выражений:

1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;

2) 3a + 2b и 2a – 3b при а = –2 и b = 4.

2. Запишите в виде двойного неравенства: р отрицательно и больше –18.

Скачано с www.znanio.ru