Среднее значение. Дисперсия. Станд откл_Методические рекомендации к уроку №7

Методические рекомендации к проведению урока

Тема урока: Среднее значение. Дисперсия. Стандартное отклонение

Тип урока: урок закрепления знаний

Цели обучения:

8.3.3.5

знать определения и формулы для вычисления дисперсии и стандартного отклонения;

Цели урока:

Учащиеся могут

·         объяснить суть дисперсии и стандартного отклонения;

·         вычислять дисперсию;

·         вычислять стандартное отклонение.

Структура урока

1.    Организационный момент. Целеполагание.

2.    Повторение теоретического материала.

3.    Решение задач.

4.    Углубление изучаемой темы.

5.    Самостоятельная работа.

6.    Подведение итогов урока. Рефлексия.

Теоретический материал к уроку, определения к понятиям и др.

Меры центральной тенденции.

МОДА числового ряда – это число, которое встречается в этом ряду наиболее часто.

МЕДИАНА числового ряда – это число этого ряда (или полусумма двух его чисел), слева и справа от которого на числовой прямой лежит одинаковое количество членов ряда (для нахождения медианы ряд должен быть ранжирован).

СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ – сумма всех элементов ряда, деленная на их количество.

Меры рассеивания.

РАЗМАХ – это разность наибольшего и наименьшего значений ряда данных

ДИСПЕРСИЯ – среднее арифметическое квадратов отклонений от среднего значения называется в статистике набора чисел.

Есть другой способ вычисления дисперсии: нужно сначала вычислить среднее арифметическое самих чисел, затем — среднее арифметическое их квадратов, и наконец, из среднего арифметического квадратов вычесть квадрат среднего арифметического. Учитель вводит новую формулу для вычисления дисперсии числового ряда:

СРЕДНЕЕ КВАДРАТИЧНОЕ ОТКЛОНЕНИЕ (СТАНДАРТНОЕ ОТКЛОНЕНИЕ) равно квадратному корню из дисперсии

.

Среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Инструкции к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с помощью презентации PowerPoint. Слайды презентации содержат анимации, которые позволяют поэтапно вывести на экран решения и ответы к предложенным заданиям. Поэтому при показе презентации следует делать паузы после демонстрации заданий и постановки вопросов, давая учащимся время на их выполнение и обдумывание ответов.

Задания, оформленные отдельным приложением, несмотря на то, что они включены в презентацию, необходимо предоставить учащимся обязательно в распечатанном виде.  А имеющиеся слайды использовать при обсуждении с классом и при оценивании выполненной работы. Это поможет свести к минимуму использование интерактивной доски.

Дополнительные методические рекомендации по организации урока.

При выполнении заданий целесообразно предложить учащимся использовать калькулятор, такой вид заданий отмечен в презентации следующим изображением:

Дополнительные разноуровневые (на дифференциацию) задания.

Базовый уровень

Для проверки упаковочной машины, были взяты упакованные ею некоторые коробки со спичками. Распределение количества спичек в коробках, взятых на проверку, представлены в виде таблицы.

Найдите среднее значение количества спичек в коробке и стандартное отклонение количества спичек в одной коробке.

Продвинутый уровень

Имеются два аппарата по взвешиванию сахара. При контроле взвешивания на них были получены следующие данные. (указаны в кг)

Аппарат А.

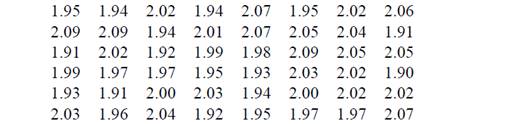
Аппарат В.

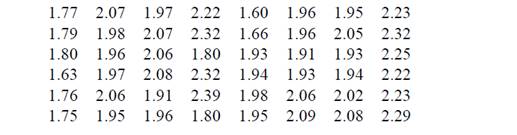
Какой из аппаратов работает более стабильнее?

Рекомендации по формативному оцениванию.

Формативное оценивание производится на каждом этапе урока (самооценивание, оценивание учителем по критериям). Оценка путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием в диалогах. Прогресс, ответную реакцию на задания в парах, в группах необходимо отслеживать для того, чтобы оценить вклад каждого ученика и выявить наличие ошибок для их дальнейшей коррекции.

Ответы, критерии к заданиям, дополнительные материалы к уроку.

Ответы к заданиям содержатся в презентации урока и полезны для организации самооценивания или взаимооценивания учащихся.

Критерии оценивания к каждому блоку заданий прописаны в приложениях к уроку, а также указаны в краткосрочном плане.

Список полезных ссылок и литературы.

Алгебра. Элементы статистики и теории вероятностей. 7-9 классы. Макарычев Ю. Н., Миндюк Н. Г. / Под.ред. Теляковского С. А. 3-е изд. - М.: Просвещение, 2005. - 78 с. 

Алгебра и начала математического анализа.  10-11 классы. Мордкович А.Г. Учебник. — 10-е изд., стер. — М.: Мнемозина, 2009. — 399 с.

https://youclever.org/book/elementy-statistiki-1

https://videouroki.net/video/43-eliemienty-statistiki.html

Скачано с www.znanio.ru