Статья "Алгоритм Евклида"

Алгоритм Евклида и основная теорема арифметики статья

Арифметика изучает свойства натуральных чисел 1, 2, 3, … Эти числа интересуют людей с древнейших времен, причем особое внимание всегда уделялось простым числам. Простым называется такое натуральное число, большее единицы, которое не имеет других делителей, кроме единицы и самого себя. Значение простых чисел заключается в том, что любое натуральное число, большее единицы, является простым либо разлагается в произведение простых. свойство единственности разложения на простые множители.

Предпосылки основной теоремы арифметики берут свои истоки в Древней Греции. Несмотря на то, что в древнегреческой математике основная теорема арифметики в современной формулировке не встречается, в «Началах» Евклида есть эквивалентные ей предложения. Прежде чем начать изучение Алгоритма Евклида мне бы хотелось узнать больше о самом математике.

Евклид — первый математик Александрийской школы. Его главная работа «Начала» содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел; в ней он подвёл итог предшествующему развитию древнегреческой математики и создал фундамент дальнейшего развития математики. Начала состоят из тринадцати книг:

1.     В I книге изучаются свойства треугольников и параллелограммов; эту книгу венчает знаменитая теорема Пифагора для прямоугольных треугольников.

2.      Книга II посвящена «геометрической алгебре».

3.     В III и IV книгах излагается геометрия окружностей, а также вписанных и описанных многоугольников;

4.     В V книге вводится общая теория пропорций.

5.      В VI книге она прилагается к теории подобных фигур.

6.     VII—IX книги посвящены теории чисел

7.     ВVIII книги рассматриваются теоремы о пропорциях и геометрических прогрессиях, вводится метод для нахождения наибольшего общего делителя двух чисел (известный ныне как алгоритм Евклида),

8.     В X книге, строится классификация иррациональностей

9.     В XI книге содержатся основы стереометрии.

10. В XII книге с помощью метода исчерпывания доказываются теоремы об отношениях площадей кругов, а также объёмов пирамид и конусов;.

11. XIII книга посвящена построению пяти правильных многогранников.

  Теперь узнав  немного об выдающемся математике можно переходить на изучение Алгоритма Евклида. Но в первую очередь   нам надо узнать : «Что же такое алгоритм Евклида и в каком виде она нам знакома?»

И так, Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.

Не подозревая еще со школьной скамьи мы работали с теоремой Евклида в школе. Данная теорема известна нам в виде(НОД).Теперь нам следует  вспомнить, что такое НОД  и алгоритм его нахождения.
Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.

Алгоритм нахождения НОД делением

1.     Большее число делим на меньшее.

2.     Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).

3.     Если есть остаток, то большее число заменяем на остаток от деления.

4.     Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30/18 = 1 (остаток 12)
18/12 = 1 (остаток 6)
12/6 = 2 (остаток 0). Конец: НОД – это делитель. НОД (30, 18) = 6

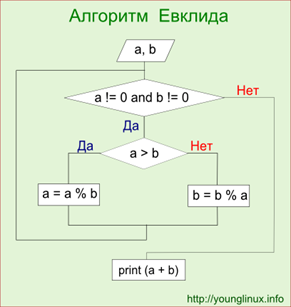Сейчас мы рассмотрели нахождение НОД делением, но нам не следует забывать о вычитании, которое также имеет важную роль.

Алгоритм нахождения НОД вычитанием

1.     Из большего числа вычитаем меньшее.

2.     Если получается 0, то значит, что числа равны друг другу и являются НОД (следует выйти из цикла).

3.     Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.

4.     Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 - 18 = 12
18 - 12 = 6
12 - 6 = 6
6 – 6 = 0 Конец: НОД – это уменьшаемое или вычитаемое. НОД (30, 18) = 6

Теперь нам необходимо познакомится с Простыми числа. Теоремы Евклида.

Число, большее единицы, называется простым, если оно имеет всего два делителя – единицу и само это число. Любое число, кроме единицы, является либо простым, либо составным.

·        Первая теорема Евклида Если произведение двух чисел делится на простое число 𝑝, то хотя бы одно из них делится на 𝑝

Доказательство: Пусть 𝑎𝑏. . .𝑝 и 𝑎 не делится на 𝑝. Пусть также 𝑐 = НОД(𝑎, 𝑝). Тогда 𝑐 ≤ 𝑝 как НОД. Так как 𝑎 не делится на 𝑝 и 𝑎 делится на 𝑐, то 𝑐 ̸= 𝑝, следовательно, 𝑐 < 𝑝. Следовательно, 𝑝 > 𝑐 и 𝑝 . . .𝑐. Из определения простого числа следует, что в этом случае 𝑐 = 1, то есть НОД(𝑎, 𝑝) = 1. Тогда НОД(𝑎𝑏, 𝑏𝑝) = 𝑏. Так как 𝑎𝑏. . .𝑝 и 𝑏𝑝. . .𝑝, то 𝑝 является общим делителем 𝑎𝑏 и 𝑏𝑝, следовательно, НОД(𝑎𝑏, 𝑏𝑝) . . .𝑝, то есть 𝑏 . . .𝑝

Пример:

Условие

Автор: Голованов А.С.

Для натурального a обозначим через P(a) наибольший простой делитель числа  a² + 1. 
Докажите, что существует бесконечно много таких троек различных натуральных чисел a, b, c, что  P(a) = P(b) = P(c).

Решение

  Пусть p – нечётное простое число, а  a < p  – такое натуральное число, что  a² + 1  кратно p; тогда числа a и  p – a  различны, и  P(a) = P(p – a) = p.  Действительно, числа  a² + 1  и  (p – a)² + 1 = (a² + 1) + p(p – 2a)  делятся на pи меньше p²; значит, они не могут делиться на простые числа, большие p.  Дальше можно рассуждать по-разному.

  Первый способ. Предположим противное. Тогда существует лишь конечное число простых чисел p, для которых уравнение  P(x) = p  имеет хотя бы три натуральных решения. Обозначим через s максимальное такое простое число (если таких простых не существует, положим  s = 2),  а через S – произведение всех простых чисел, не превосходящих s.
  Пусть  p = P(S);  тогда p взаимно просто с S и потому  p > s.  Пусть a – остаток от деления S на p; тогда  a² + 1  кратно p, значит,  P(a) = P(p – a) = p.  Одно из чисел a и  p – a  чётно; обозначим его через b.
  Число  (b + p)² + 1  делится на 2p (b чётно, а p – нет), поэтому  q = P(b + p) ≥ p. 
  Если  q = p,  то уравнение  P(x) = p  имеет три решения – b,  p – b,  p + b;  а это невозможно по предположению.
  Если  q > p,  число  (b + p)² + 1 делится на 2pq. Это означает, что  q < b + p  (в противном случае  (b + p)² + 1 ≤ (2p – 1)q + 1 < 2pq).  Обозначая через c остаток от деления числа  b + p  на q, получаем  P(c) = P(q – c) = P(b + p) = q > p > s,  что противоречит выбору s.

·        Существование простого делителя. Любое число, большее единицы, имеет хотя бы один простой делитель

Доказательство: Пусть 𝑛 – наименьшее число, большее единицы и не имеющее простого делителя. Тогда число 𝑛 не может быть простым, в противном случае, оно имело бы простой делитель 𝑛. Так как число 𝑛 не является простым, то оно имеет хотя бы один делитель среди чисел от 2 до 𝑛 − 1, но все эти числа имеют хотя бы один простой делитель, следовательно, число 𝑛 должно иметь хотя бы один простой делитель.

·        Вторая теорема Евклида. Множество простых чисел бесконечно Доказательство: Пусть 𝑝1, 𝑝2, ..., 𝑝𝑛 – все простые числа. Тогда число 𝑎 = 𝑝1𝑝2...𝑝𝑛 + 1 больше каждого из этих чисел. Кроме того число 𝑎 не делится ни на одно из чисел 𝑝𝑖 . Однако, любое число, большее единицы, должно иметь хотя бы один простой делитель, следовательно, множество 𝑝1, 𝑝2, 4 ..., 𝑝𝑛 не содержит все простые числа. Получается противоречие, следовательно множество простых чисел бесконечно.

 Данный алгоритм остаётся актуальным до сих пор, он применяется в классической теории чисел, точнее в теории делимости. его рассматривают не только в кольце целых чисел, но также и в кольце многочленов, широкое применение имеет и бинарный алгоритм Евклида.

Список литературы:

• Абрамов С. Самый знаменитый алгоритм // Квант. — 1985. — № 11. — С. 44—46.
• Виноградов И. М. Основы теории чисел.
• Курант Р., Роббинс Г. Дополнение к главе I, § 4. // Что такое математика?. — 3-e изд., испр. и доп.. — М., 2001. — 568 с.
• Щетников А. И. Алгоритм Евклида и непрерывные дроби. Новосибирск: АНТ, 2003.

Автор статьи: Савчук Александра , студент СурГПУ , группа Б-8022

Скачано с www.znanio.ru