Стаья на тему: "Обобщенный вариант уравнения Бюргерса"

Обобщенный вариант уравнения Бюргерса.

Гаджимирзаев М.М.,

учитель математики РЦДОДИ.

E-mail: [email protected]

Аннотация. Уравнение Бюргерса, предложенное первоначально для описания турбулентности, оказалось удачной моделью динамики нелинейно-диссипативных сред различной физической природы. Хорошо известно, что это уравнение непосредственно возникает при рассмотрении различных процессов в гидродинамике, нелинейной акустике и физике плазмы. В настоящей работе рассматривается обобщенный вариант уравнения Бюргерса и для частных случаев этого уравнения рассмотрена задача Коши.

Ключевые слова: уравнение Даламбера, уравнение Бюргерса, задача Коши.

1.     Введение

Волновые процессы являются эффективным средством пе­редачи энергии и информации. Они широко используются в науке и технике. Поэтому исследование закономерностей рас­пространения волн различной природы является важной и ак­туальной задачей. При изучении процесса распространения плоских волн раз­личной природы в качестве исходного соотношения выберем закон сохранения, записанный в универсальной форме

                                        (1)

в которой  - некоторая характеристика состояния среды, например плотность массы, импульса или энергии, a q - плот­ность потока, связанная с  и  функциональным соотношением , конкретный вид которого зависит от выбора физического механизма переноса массы, импульса или энергии. В случае, когда , где  - некоторая постоянная, уравнение (1) приводится к линейному дифференциальному уравнению в частных производных первого порядка

                                           (2)

решение которого

                                                           (3)

описывает волну неизменного профиля, распространяющуюся со скоростью  в положительном направлении оси Ох.

Если же , то мы переходим в область нелинейных волн, причем в первом приближении нелинейность конвектив­ного механизма переноса можно учесть, считая

                              .                                (4)

Подставив выражение (4) в (1), получим обобщенное урав­нение (92) в виде

                                                      (5)

Переходя к новым переменным  и , преобразуя производные

и опуская штрихи у новых переменных, получаем нелинейное уравнение Римана

Если в механизме переноса кроме конвективной составляющей учесть и диффузионную составляющую плотности потока   положить в законе сохранения (1)

то после несложных преобразований получим нелинейное уравнение

Это уравнение в математической физике называют уравнением Бюргерса (см., например, [1,2]). Важный результат для уравнения Бюргерса был получен Хопфом и Коулом [3,4], которые показали, что нелинейное уравнение Бюргерса (7) с помощью замены

                                  (8)

сводится к линейному уравнению теплопроводности

Действительно, если в уравнении (9) перейти от функ­ции  к функции  , то с учетом преобразований

 из (9) получим уравнение для функции :

 Продифференцировав это уравнение по , запишем его в виде

Теперь, обозначив производную   через , для функции

получим уравнение Бюргерса

Таким образом, с помощью замены Коула-Хопфа каждое решение  линейного уравнения теплопроводности (9) порождает решение  нелинейного уравнения Бюр­герса (7). Теперь перейдем к обобщенному варианту уравнения Бюргерса.

2.     Обобщенный вариант уравнения Бюргерса

В [2] исследовано уравнение Бюргерса

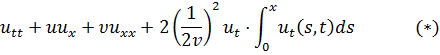
которое можно перезаписать в виде:

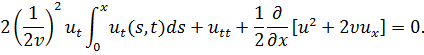
В результате замене это уравнение, сводится к уравнению Даламбера. Имеем

Подставляя в уравнение место  получим

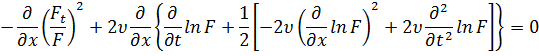
Что равносильно при  уравнению

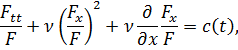
где произвольная функция. Осуществляя, дифференцирование получим:,  что равносильно  неоднородному линейному уравнению теплопроводности, которое  при совпадает с уравнением Даламбера, если и Пуассона при .

Далее рассмотрим уравнение

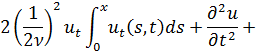
              (10)

которое при  совпадает с уравнением, изученным выше (*).  Естественно (10) считать обобщенным вариантом уравнения (*). Отметим, что в случае когда , уравнение (10) принимает вид

Если в (11) вести замену     

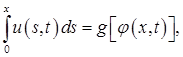                                                                                 (12)

то относительно неизвестной ,получим

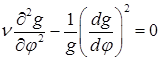                                                .                                (13)

Непосредственно проверкой можно убедится в том, что решение (13) имеет вид:

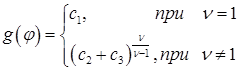                                                    (14)

где произвольные постоянные.

Не ограничивая общности можно получает.  , а  Тогда применяя к (7) замену из (10) получим замену

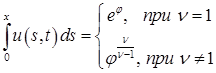                                                                        (15)

в результате применения которой (10) при  сводится к уравнению

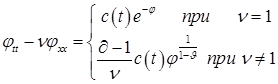                                                           (16)

Если считать произвольную функцию , то (16) является уравнением Даламбера при и Пуассона при  с вытыкающимися отсюда последствиями корректности постановки задачи Коши и (СКЗ) Дирихле - Неймана для уравнения (11). Например, задача Коши для уравнения (11) с начальными условиям    сводится к решению задачи Коши для обычного уравнения Даламбера  с начальным условиям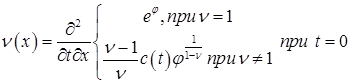                                            

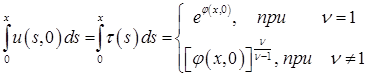
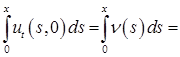
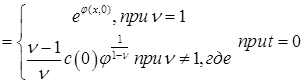
ил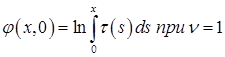и

          и         .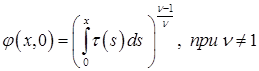

Библиографический список

1.     Burgers J.M. A mathematical model illustrating theory of turbulence // Adv. Appl. Mech. 1948. Vol. 1. P. 171–199.

2.     Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М.: Наука, 1979. 384 с.

3.    Hopf E. The partial differential equation  // Comm. Pure Appl. Math. 1950. Vol. 3. P. 201–230.

4.     Cole J. D. On a quasilinear parabolic equation occurring in aerodynamics // Quart. Appl. Math. 1951. Vol. 9. P. 225–236.