Сценарий урока математики в 5 классе по теме «Прямая на плоскости»

 

Урок математики в 5 классе

Тема урока: «Прямая на плоскости»

Тип урока: открытие нового знания

Форма проведения урока: урок-исследование

Технологии: деятельностный метод Л.Г. Петерсон, информационно-коммуникационные, игровые.

Основные цели:

1) сформировать умение выводить свойства на основе ранее полученных знаний;

2) сформировать умение распознавать взаимное расположение прямых на плоскости;

3) тренировать универсальные учебные действия;

4) сформировать мотивацию к учебной деятельности как одно из средств развития и социализации личности учащихся.

Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, обобщение, классификация.

Оборудование: проектор, компьютер, экран, слайды презентации.

Демонстрационный материал: 1) сопровождающая презентация; 2) кластер — эталон.

Раздаточный материал: 1) кластер — эталон, 2) инструментарий, приводящий к открытию нового знания, 3) карточка-задание для первичного закрепления с проговариванием, 4) карточка-задание для проведения самостоятельной работы на этапе первичного закрепления знания с последующей самопроверкой, 5) смайлики для этапа рефлексии.

 

 

 

 

Ход урока

1. Мотивация к учебной деятельности.

− Ребята, Здравствуйте. Сегодня мы вновь отправляемся в путешествие по стране Знаний, чтобы открыть что-то новое, для вас еще непознанное.

Айвен Нивен (1915—1999) — канадско-американский математик, специалист в теории чисел сказал: «…Математику нельзя изучать, наблюдая, как это делает сосед!...»

Поэтому девизом нашего сегодняшнего урока давайте выберем следующие слова:

Думать – коллективно!

Решать – оперативно!

Отвечать – доказательно!

Бороться – старательно!

И открытия нас ждут обязательно!

 

- Какие же открытия ждут нас сегодня? С чем новым мы сегодня познакомимся? Давайте же это выясним. Сделать это нам поможет игра. Поиграем и разгадаем ребусы:  (ПЛОСКОСТЬ)

 (ПРЯМАЯ)

 

2. Актуализация знаний

- Что же такое плоскость и прямая? (Геометрические фигуры)

- Какие предметы или явления в окружающем мире дают нам представление об этих фигурах? (Крышка стола, лист бумаги, гладь озера, провода, натянутая веревка и т.п.)

- А как вы думаете, ребята, связаны ли эти фигуры друг с другом? (Да)

- А как? Кто из них «важнее»? (Прямая располагается на плоскости, и обе фигуры важны в геометрии)

− Скажите, чему же будет посвящен сегодняшний урок? (Изучению прямой и плоскости, исследованию как прямые располагаются на плоскости)

- Как мы сформулируем тему нашего урока? (Прямая на плоскости). Запишите в тетрадях сегодняшнее число и тему урока.

− Какую же цель вы поставите перед собой? (Узнать, что такое прямая и плоскость и выяснить каким может быть их взаимное расположение)

− А как вы узнаете новое на уроке? (Мы сначала повторим то, что нам понадобится, обобщим, выполним пробное задание, у нас может не получиться, мы остановимся, подумаем и сами откроем новое знание.)

− Как вы будете работать? (Самостоятельно.)

− Тогда пожелайте друг другу удачи − и в путь.

3. Фиксирование индивидуального затруднения в пробном действии.

− Какое задание я вам сейчас предложу? (Пробное действие)

− Можете ли вы сказать ответить на следующий вопрос: Как могут располагаться прямые на плоскости?

 Обучающиеся могут предложить свои варианты. Тогда учитель просит показать, или изобразить возможные варианты. При этом ученики испытывают затруднение.

4. Выявление места и причины затруднения.

− Как вы рассуждали? На какие знания вы опирались в своих действиях?

− Подошли ли к вашему заданию известные вам факты, представления? (Нет.)

− Где же возникло затруднение? Что мы не знаем? (Я пока не могу объяснить, как могут располагаться прямые на плоскости. Я пока многое не знаю о расположении прямой на плоскости)

5. Построение проекта выхода из затруднения.

− Прежде чем продолжить работу дальше, что надо сделать? (Поставить цель.)

− Сформулируйте цель своей деятельности. (Узнать, как могут располагаться прямые на плоскости, составить памятку.)

− Как вы будете открывать новое, используя ранее изученное? (Давайте составим план).

− Составим план вашей дальнейшей работы.

 

На доске фиксируется план:

1. Пояснить (объяснить) что такое прямая?

2. Как изобразить прямую, какие инструменты использовать, как назвать (обозначить) прямую?

3. Изобразить разные прямые на плоскости и исследовать как они могут располагаться?

6. Реализация построенного проекта.

- Давайте определим, какая фигура называется прямой. Чтобы вспомнить и указать ее особенности можно запомнить следующую считалочку:

Без конца она, без края
Эта линия прямая.
Хоть 100 лет по ней идти
Не найдёшь конца пути.

 

Учитель демонстрирует на слайде построение прямой с помощью линейки, анимация показывает, что ее можно продолжить в обе стороны бесконечно. Показывается построение и обозначение прямой разными способами.

 

 

 

 

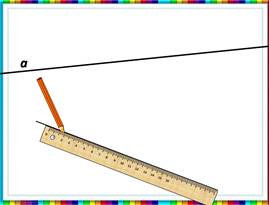
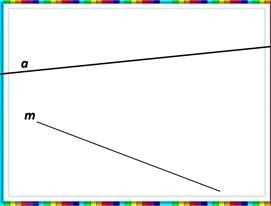
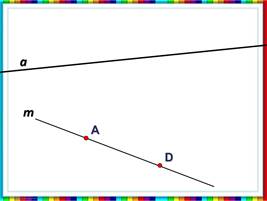
Обучающиеся выполняют построение в тетради, обозначают прямые разными способами: прямая а, прямая m, прямая AD.

 

- А теперь, дети, давайте займемся исследованием. Вы, выполняя практические задания, сможете самостоятельно сделать выводы. А поможет вам в этом групповая работа. Работать вы будете в группах по 4-5 человек. На работу в группах отводится 10-12 минут. Каждой группе предоставляется инструментарий для открытия нового знания (раздаточный материал – инструментарий).

1. Проведите через точку А прямую а.

 

 

 

 

2. Можно ли через эту же точку провести еще одну прямую b? Если да, то проведите.

3. Сколько можно провести прямых через одну точку? Если можно еще провести прямые, проведите их.

4. Сделайте вывод:

«Через одну точку на плоскости можно провести _____________________________________ прямых».

5. Проведите прямую через две точки А и В.

 

 

 

 

 

Можно ли через эти же точки провести другую прямую? Если да, то проведите. Сделайте вывод:

«Через две точки на плоскости можно провести _____________________________________».

6. Продолжите прямые на листе как только возможно

 

 

 

 

 

Сформулируйте предположение: «На плоскости есть прямые, у которых нет ________________ точек, или которые не ______________________».

 

 

Обучающиеся начинают работу. Учитель выступает в качестве помощника и консультанта.

 

Физкультминутка.

 

 

По истечении времени, отведенного на выполнение заданий, проводится проверка всех выполненных шагов с фиксацией выводов в тетради. С места отвечают по одному представителю от группы.

В тетрадях обучающиеся фиксируют следующие выводы:

«Через одну точку на плоскости можно провести бесконечно много прямых».

«Через две точки на плоскости можно провести только ОДНУ прямую».

«На плоскости есть прямые, у которых нет общих точек, или которые не пересекаются».

 

- Давайте, теперь попробуем ответить на вопрос пробного действия: как могут располагаться прямые на плоскости? (Прямые могут иметь только одну общую точку, в этом случае они называются пересекающимися, могут иметь более одной общей точки, и тогда они будут совпадать, а могут не иметь общих точек)

 

В процессе обсуждения и формулировки выводов на слайдах презентации последовательно выстраивается кластер (карта ума), которая будет использоваться обучающимися в качестве эталона по распознаванию взаимного расположения прямых на плоскости. Данный эталон выдается ученикам в печатном виде, они вклеивают его в свою тетрадь.

 

 

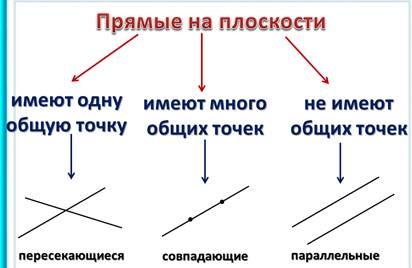
При составлении эталона дети фиксируют в тетради определения пересекающихся, совпадающих и, новое определение, параллельных прямых.

 

Прямые, имеющие одну общую точку, называются пересекающимися.

Прямые, имеющие много общих точек, называются совпадающими.

Прямые, не имеющие общих точек, называются ПАРАЛЛЕЛЬНЫМИ.

 

(обратить внимание обучающихся на правильность написания математических понятий)

 

Физкультминутка для глаз.

 

− Можете ли вы теперь описать взаимное расположение прямых на плоскости, что вам в этом поможет?  (Да, карта ума)

− А можете изобразить прямые по описанию? (Будем пробовать, ведь изображать и обозначать прямые мы умеем)

− А что будет труднее всего изобразить? (Параллельные прямые)

- А вот этот материал мы будем изучать позднее и научимся с помощью дополнительных чертежных инструментов проводить параллельные прямые. А пока будем проводить их, если нам потребуется, как? (На глаз, т.е. приблизительно)

7. Первичное закрепление с проговариванием во внешней речи.

− Рассмотрите выданный вам раздаточный материал. Давайте выполним задания и закрепим полученное новое знание. Помните, что поможет вам правильно ответить на вопросы составленная нами карта ума.

Задание 1: Назовите какие прямые пересекаются, а какие параллельны.

 

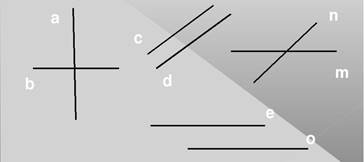
Обучающиеся проговаривают название прямых и их взаимное расположение, объясняя, почему именно этот вывод они сделали об указанных прямых. Например, прямые а и b пересекаются, или пересекающиеся, так как имеют только одну общую точку; прямые е и о параллельные, так как не имеют общих точек.

 

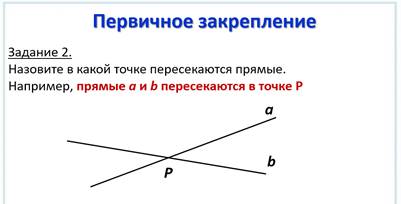
Задание 2: Назовите в какой точке пересекаются прямые.

                   

 

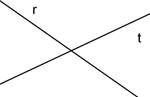
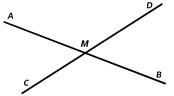
Предварительно на слайде можно привести пример правильного ответа

 

Задание 3.

Проведите прямые k и p, пересекающиеся в точке N.

Задание 4.

Проведите параллельные прямые АВ и СD.

 

При выполнении заданий 3 и 4 учитель вызывает одного обучающегося к доске после того, как остальные выполнили в тетрадях. Учитель оказывает помощь тем, кто испытывает затруднения.

После первичного закрепления материала можно еще раз вернуться к пробному действию и, используя эталон, еще раз проговорить варианты взаимного расположения прямых на плоскости.

 

8. Самостоятельная работа с самопроверкой.

− Мы поработали вместе, вы поработали в группах, а что теперь необходимо сделать? (Поработать самостоятельно.)

− С какой целью вы будете работать самостоятельно? (Мы должны для себя выяснить, понятно ли нам новое знание и  можем ли мы им самостоятельно пользоваться.)

 

Обучающиеся выполняют задания на карточке: заполняют пропуски в таблице и пустографке, а также обозначают точки на приведенном рисунке.

 

Задание 1: Заполните пустые места.

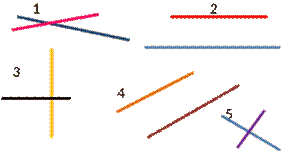
На рисунке 1 изображены		прямые
На рисунке 2 изображены		прямые
На рисунке 3 изображены		прямые
На рисунке 4 изображены		прямые
На рисунке 5 изображены		прямые

 

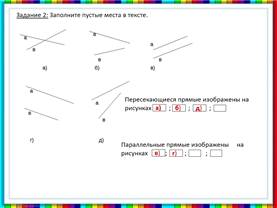
Задание 2: Заполните пустые места в тексте.

 

 

 

 

 

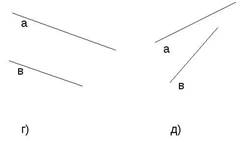
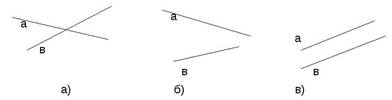
Пересекающиеся прямые изображены на рисунках  

                    ;           ;           ;

Параллельные прямые изображены     на рисунках

                     ;           ;           ;

 

 

 

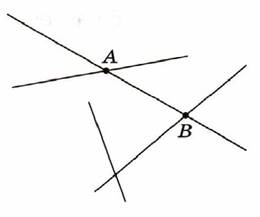
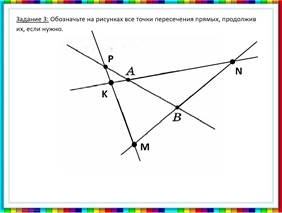
Задание 3: Обозначьте на рисунках все точки пересечения прямых, продолжив их, если нужно.

 

 

 

 

 

 

 

 

– Проверьте.

 

Открыть на слайде эталон для самопроверки:

 

 

 

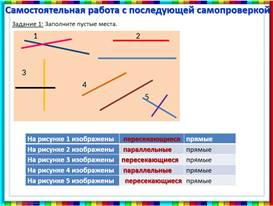
– В каждом задании у кого получился другой ответ – поставьте «?», найдите место, где допущена ошибка, постарайтесь объяснить, почему она возникла.

– Кто справился с заданием без ошибок? Поставьте себе «+».

 

Учитель обращает особое внимание на задание 3, направленное на включение нового знания в систему. В данном задании обучающиеся могут допустить наибольшее количество ошибок по причине того, что не догадаются, что прямые необходимо продолжить. Поэтому еще раз надо обратиться к понятию прямой, вспомнить считалочку.

9. Рефлексия учебной деятельности на уроке.

– Какими же могут быть прямые на плоскости? (Совпадающими, пресекающимися, параллельными)

− Назовите, по какому признаку вы распознаете прямые на плоскости? (По количеству общих точек)

- Сформулируйте новые понятия?

− Какие цели вы сегодня ставили?

− Достигли вы этих целей? Докажите.

− Удалось ли нам решить поставленные задачи?

− Что на уроке у вас хорошо получалось?

− У кого остались затруднения по новой теме?

− Над чем еще вам надо будет поработать?

− Можно ли сказать, что сегодня вы были настоящими учениками? (Да.)

− Докажите.

− Оцените свою работу на уроке, используя смайлики.

 

 

 

Далее учитель предлагает обучающимся обсудить домашнее задание.

 

− Спасибо за урок! До новых встреч и новых открытий!

Петрова Наталья Викторовна,

учитель математики высшей категории

 МКОУ Заволжского лицея

г. Заволжск Ивановская область

 

Скачано с www.znanio.ru