^{y = f(x)}      f(x) = x², f(x) = sin x, f(x) = 3x + 1 где:

x — независимая переменная (аргумент) y — зависимая переменная (значение функции).

Область определения D(f) — множество всех допустимых значений аргумента x, при которых функция имеет смысл.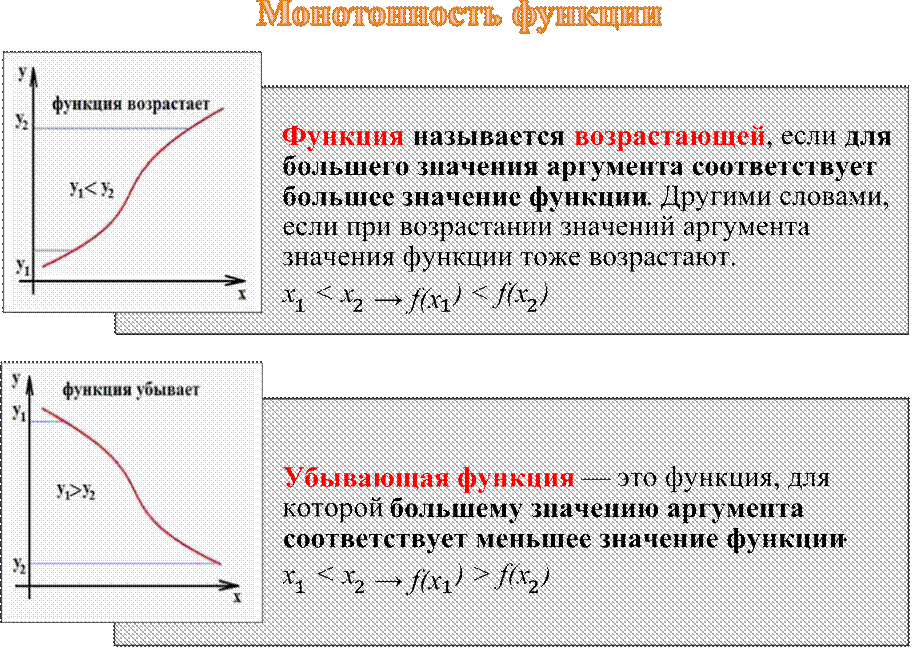

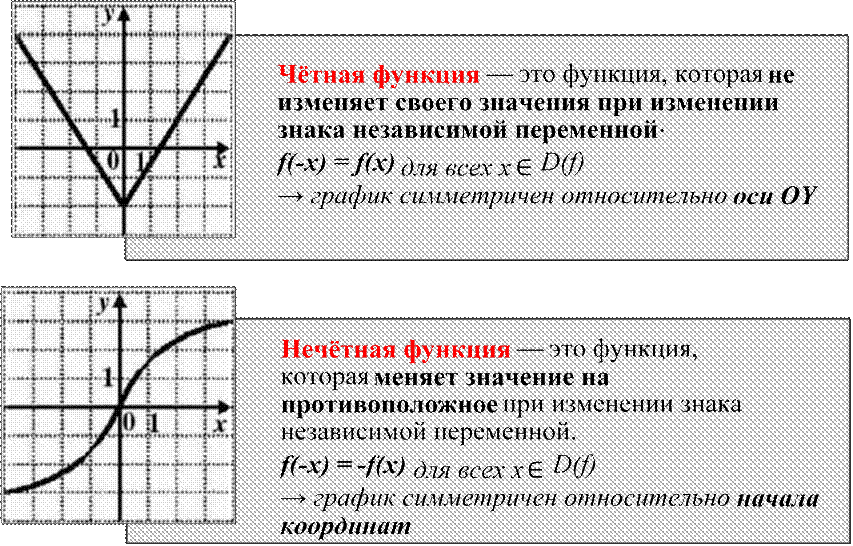Примеры: Четные:

•f(x) = x²,

•f(x) = cos x

•f(x) = x³,

•f(x) = sin x

Ни те, ни другие:

•f(x) = x² + x

Периодическая функция

функция, которая повторяет свои значения через некоторый

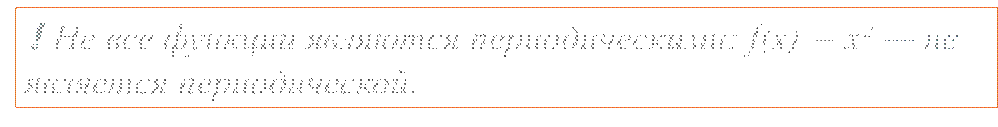❗Не все функции являются периодическими: f(x) = x² — не является периодической.

определение

Функция называется ограниченной, если множество её значений ограничено при всех значениях аргумента.

Иначе говоря, существует такое положительное число М, что для всех значений x из области определения функции выполняется неравенство |f(x)| ≤ M. Если такого числа М не существует, то функция называется неограниченной.

неограниченная функция —

Функция, ограниченная функция, которая не

сверху — это функция, область удовлетворяет условиям

значений которой ограничена ограниченности (сверху или

сверху некоторым числом. снизу).

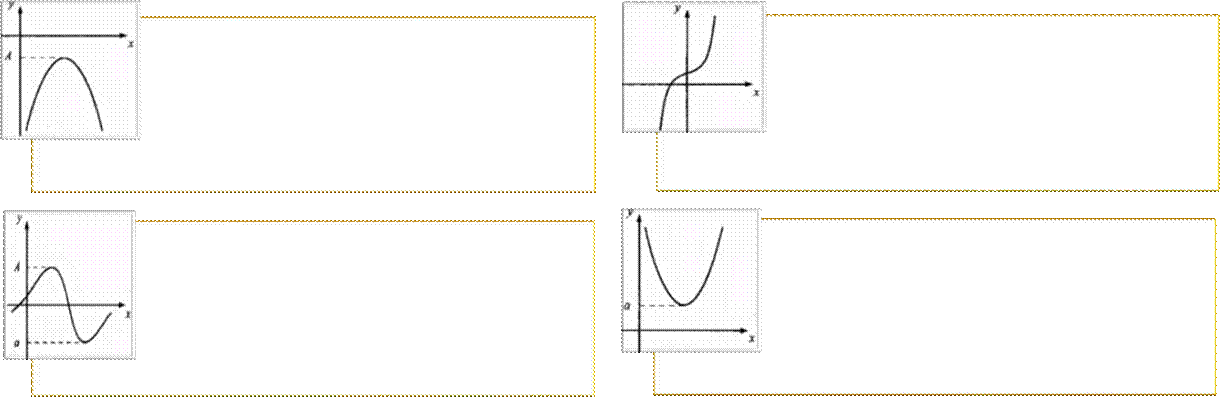Функция, ограниченная снизу — это функция, значения которой не могут быть меньше некоторого числа.

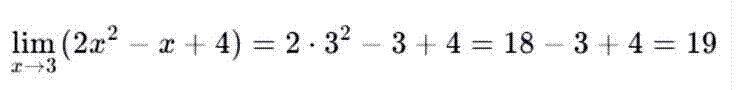
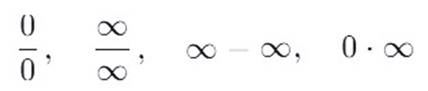
Основные методы раскрытия:

•Разложение на множители

•Умножение на сопряжённое выражение

•Деление числителя и знаменателя на старшую степень x (при x→∞ )

•Применение замечательных пределов

Функция f(x) называется непрерывной в точке x=a , если выполняются три условия:

Примеры непрерывных функций:

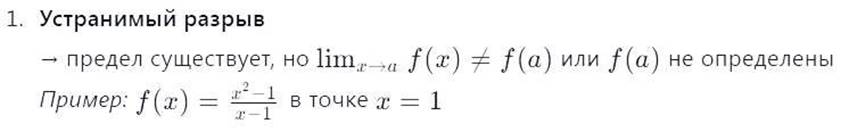
2.   Разрыв I рода (скачок)

→ существуют конечные, но разные односторонние пределы

3.   Разрыв II рода

→ хотя бы один из односторонних пределов не существует или бесконечен                                        

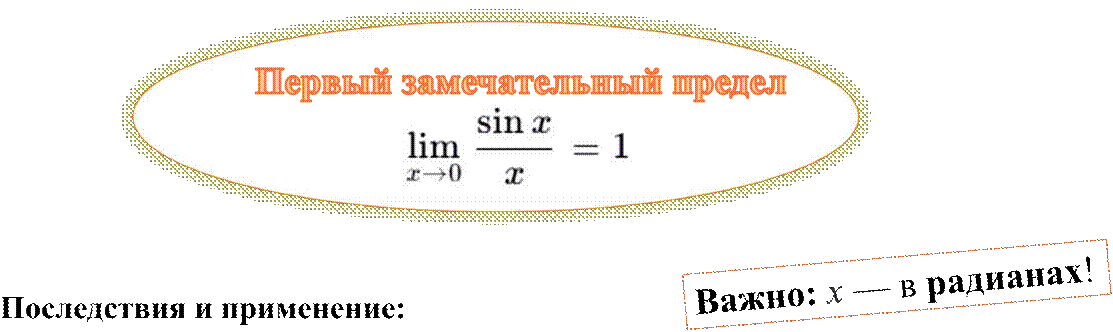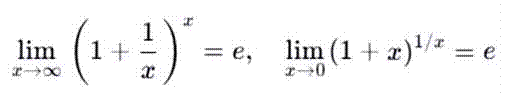 , где e≈2,71828... — основание натурального логарифма

Обобщённая форма:

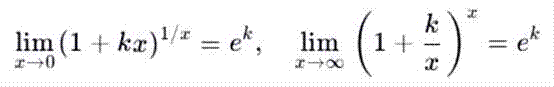
Примеры:

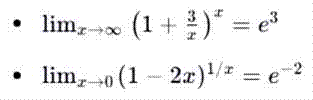
•           Основа математического    анализа   —  без   пределов  невозможно

определить производную и интеграл.

•           Исследование функций — асимптоты, поведение в особых точках,

построение графиков.

•           Физика — мгновенная скорость, ускорение, плотность.

•           Экономика — предельные издержки, доход, эластичность.

•           Инженерия и IT — моделирование, численные методы, машинное обучение.

Краткий вывод