Тема: «Способы решения логарифмических уравнений». 10 класс

Тема:    «Способы решения логарифмических уравнений».

Предмет	Алгебра и начала математического анализа
Класс	10
Тема урока	«Способы решения логарифмических уравнений», 2 часа
Базовый учебник	Ш.А. Алимов, Ю.М. Колягин и др. / М. Просвещение 2014

Цель  урока: повторить знания учащихся о логарифме числа, его свойствах; изучить способы решения логарифмических уравнений и закрепить их при выполнении упражнений.

Задачи:

- обучающие: повторить определение и основные свойства логарифмов, уметь применять их в вычислении логарифмов, в решении логарифмических уравнений;

-развивающие: формировать умение решать логарифмические уравнения;

-воспитательные: воспитывать настойчивость, самостоятельность; прививать интерес к предмету

Тип урока:  урок изучения нового материала. 

Необходимое техническое оборудование: компьютер, проектор, экран.

Структура и ход  урока:

I.       Организационный момент.

Учитель.

- Здравствуйте, садитесь!          Сегодня тема нашего урока «Решение логарифмических уравнений», на котором мы познакомимся со способами их решения, используя определение и свойства логарифмов. (слайд № 1)

II.    Устная работа.

Закрепление понятия логарифма, повторение его основных свойств и свойств логарифмической функции:

1. Разминка по теории:

 1. Дайте определение логарифма. (слайд № 2)

 2. От любого ли числа можно найти логарифм?

 3. Какое число может стоять в основании логарифма?

 4.  Функция y=log_0,8 x является возрастающей или убывающей?Почему?

 5.  Какие значения может принимать логарифмическая функция?

 6. Какие логарифмы называют десятичными, натуральными?

7. Назовите основные свойства логарифмов. (слайд № 3)

8. Можно ли перейти от одного основания логарифма к другому? Как это сделать? (слайд № 4)

2. Работа по карточка(3-4 ученика):

Карточка №1:  Вычислить: а) log₆4 + log₆9 =

                                               б) log_1/336 – log_1/312 =

                            Решить уравнение: log₅х = 4 log₅3 – 1/3 log₅27

Карточка №2: 

                           Вычислить: а) log211 – log244 =

                                                б) log1/64 + log1/69 =

                          Решить уравнение: log₇х = 2 log₇5 + 1/2 log₇36 – 1/3 log₇125.

Фронтальный опрос класса (устные упражнения)

 Вычислить: (слайд № 5)

1.      log216 2.      lоg3 √3 3.      log71   4.      log5 (1/625) 5.      log211  - log 244

6.      log814 + log 832/7 7.      log35  ∙ log53 8.      5 log5 49 9.      8 lоg 85 - 1 10.  25 –log 510

 

Сравнить числа: (слайд № 6)

1.      log_½ е и log_½π;

2.      log₂ √5/2 и log₂√3/2.

Выяснить  знак выражения log_0,83 · log₆2/3. (слайд № 7)

III.Проверка домашнего задания:

На дом были задания следующие упражнения: №327(неч.), 331(неч.), 333(2) и 390(6). Проверить ответы к данным заданиям и ответить на вопросы учащихся.

IV. Изучение нового материала:

Определение: Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим.

Простейшим примером логарифмического уравнения служит уравнение
  log_a х =с (а > 0, а≠ 1)
Способы решения логарифмических уравнений: (слайд № 8)

1.    Решение уравнений на основании определения логарифма. (слайд № 9)

log_a х = с (а > 0, а≠ 1) имеет решение  х = а^с.

На основе определения логарифма решаются уравнения, в которых:

·      по данным основаниям и числу определяется логарифм,

·      по данному логарифму и основанию определяется  число,

·      по данному числу и логарифму определяется основание.

Примеры:

log₂ 128= х,         log₁₆х = ¾,                 log_х 27= 3,

2^х= 128,               х =16 ^¾   ,                   х³ =27,

2^х = 2⁷,                 х =2 ³  ,                       х³ = 3³   ,

х =7  .                   х = 8.                          х =3.

С классом решить следующие уравнения:

а) log₇(3х-1)=2 (ответ: х=3 1/3)

б) log₂(7-8х)=2 (ответ: х=3/8).

2.    Метод потенцирования. (слайд № 10)

Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их т.е.

 log_a f(х) = log_a g(х), то f(х) = g(х), при условии, что f(х)>0, g(х)>0 , а > 0, а≠ 1.

Пример:

Решите уравнение   =

ОДЗ:

3х-1>0;                     х>1/3

6х+8>0.

3х-1=6х+8

-3х=9

х=-3

-3 >1/3 - неверно

Ответ: решений нет.

 

С классом решить следующее уравнение:

lg(х²-2) = lg х (ответ: х=2)

 

3.    Уравнения, решаемые с помощью применения основного логарифмического тождества. (слайд №11)

Пример:

Решите уравнение  =log₂(6-х)

ОДЗ:

6-х>0;

х>0;

х≠1;

log₂х²>0;

х²>0.

Решение системы: (0;1)Ụ (1;6).

 = log₂(6-х)

х² = 6-х

х²+х-6=0

х=-3 не принадлежит ОДЗ.

х=2 принадлежит ОДЗ.

Ответ: х=2

 С классом решить следующее уравнение:

 ⁼  (ответ: х=1)

 

4.    Метод приведения логарифмов к одному и тому же основанию. (слайд № 12)

Пример:

Решите уравнение  log₁₆х+ log₄х+ log₂х=7

ОДЗ: х>0

¼ log₂х+½ log₂х+ log₂х=7

7/4 log₂х=7

log₂х=4

х=16 – принадлежит ОДЗ.

Ответ: х=16.

 

С классом решить следующее уравнение:

 +  =3 (ответ: х=5/3)

 

5.    Уравнения, решаемые с помощью применения свойств логарифма. (слайд № 13)

Пример:

Решите уравнение  log₂ (х +1)  -  log₂ (х -2 ) = 2.

ОДЗ:

х+1>0;

х-2>0.         х>1.

Воспользуемся формулой преобразования разности логарифмов логарифм частного, получаем   log₂ = 2, откуда следует  = 4.

Решив последнее уравнение, находим х = 3, 3>1 - верно

Ответ: х = 3.

 

С классом решить следующие уравнения:

а)log₅  (х +1) + log₅ (х +5) = 1 (ответ: х=0).

б)log₉( 37-12х ) log_7-2х 3   =  1,

37-12х >0,                 х< 37/12,

7-2х >0,                     х< 7/2,                     х< 7/2, 

7-2х≠ 1;                     х≠ 3;                         х≠ 3;

       log₉( 37-12х ) / log₃ (7-2х )  =  1,

       ½ log₃( 37-12х ) = log₃ (7-2х ) ,

        log₃( 37-12х ) = log₃ (7-2х )² ,

        37-12х= 49 -28х +4х²  ,

        4х²-16х +12 =0,

         х²-4х +3 =0,   Д=19,   х₁=1,   х₂=3,  3 –посторонний корень .

Ответ: х=1 корень уравнения.

 

    в) lg(х²-6х+9) - 2lg(х - 7) = lg9.

 (х²-6х+9) >0,     х≠ 3,

 х-7 >0;               х  >7;             х  >7.

        lg ((х-3)/(х-7))² = lg9

((х-3)/(х-7))²    = 9,

(х-3)/(х-7) = 3,                                 (х-3)/(х-7)= - 3 ,

х- 3 = 3х -21 ,                                    х -3 =- 3х +21,

х =9.                                                       х=6 -   посторонний корень.

Проверка показывает 9 корень уравнения.              

  Ответ : 9

 

6.    Уравнения, решаемые введением новой переменной. (слайд № 14)

 Пример:

Решите уравнение    lg²х - 6lgх+5 = 0.

ОДЗ: х>0.

Пусть lgх = р, тогда р²-6р+5=0.

р₁=1, р₂=5.

Возвращаемся к замене:

lgх = 1,                                                 lgх =5

х=10, 10>0 – верно                              х=100000, 100000>0 – верно

Ответ: 10, 100000

 

С классом решить следующее уравнение:

   log₆² х  + log₆ х  +14 = (√16 – х²)² +х²,

      16 – х²  ≥0  ;      - 4≤ х ≤ 4;

       х >0 ,                    х >0,                О.Д.З. [ 0,4).    

    log₆² х  + log₆ х  +14 = 16 – х² +х²,        

      log₆² х  + log₆ х  -2 = 0

      заменим log₆ х  = t

   t ² + t -2 =0 ;        D = 9 ;      t₁ =1 ,  t₂ = -2.

 log₆ х = 1 , х = 6  посторонний корень .

 log₆ х = -2, х = 1/36 , проверка показывает  1/36 является корнем .

                                                Ответ : 1/36.

 

7.    Уравнения, решаемые с помощью разложения на множители. (слайд № 15)

Пример:

Решите уравнение log₄(2х-1)∙ log₄х=2 log₄(2х-1)

ОДЗ:

 2х-1>0;

  х >0.      х>½.

log₄(2х-1)∙ log₄х - 2 log₄(2х-1)=0

log₄(2х-1)∙(log₄х-2)=0

log₄(2х-1)=0    или    log₄х-2=0

2х-1=1                        log₄х = 2

х=1                             х=16

1;16 – принадлежат ОДЗ

Ответ: 1;16

 

С классом решить следующее уравнение:

log₃х ∙log₃(3х-2)= log₃(3х-2) (ответ: х=1)

 

8.    Метод логарифмирования обеих частей уравнения. (слайд № 16)

Пример:

Решите уравнения                    

                    

 

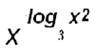Прологарифмируем обе части  уравнения  по основанию 3.

 

Получим      log₃                     =  log₃ (3х)

 

                                               .

получаем :    log₃ х² log₃ х   =  log₃ (3х),

                      2log₃ х log₃ х   =  log₃ 3+ log₃ х,

                      2 log₃² х    =  log₃ х +1,

                      2 log₃² х   -  log₃ х -1=0,

заменим log₃ х  = р ,     х >0

  2 р ² + р -2 =0 ;     D = 9 ;   р₁ =1 ,  р₂ = -1/2

 log₃ х  = 1 ,  х=3,

log₃ х  = -1/ 2 , х= 1/√3.                      

Ответ: 3 ;  1/√3

С классом решить следующее уравнение:

    log₂ х  - 1                       

х             =   64 (ответ:  х=8 ; х=1/4)

 

9.    Функционально – графический метод. (слайд № 17)

Пример:

Решите уравнения:   log₃ х = 12-х.

Так как функция у= log₃ х возрастающая , а функция у =12-х убывающая на (0; + ∞ ) то заданное уравнение на этом интервале имеет один корень.

Построим в одной системе координат графики двух функций: у= log₃ х и  у =12-х.

При  х=10  заданное уравнение обращается в верное числовое равенство 1=1. Ответ х=10.

С классом решить следующее уравнение:

1-√х =ln х (ответ : х=1).

 

V.    Подведение итогов, рефлексия (раздать кружочки, на которых ребята отмечают свое настроение рисунком). (слайд № 18,19)

Определить метод решения уравнения:

 

 

 

 

 

VI. Домашнее задание: 340(1), 393(1), 395(1,3), 1357(1,2), 337(1), 338(1), 339(1)

Литература

1. Рязановский, А.Р. Математика. 5 – 11 кл.: Дополнительные материалы  к уроку математики/ А.Р.Рязановский, Е.А.Зайцев. – 2-е изд., стереотип. – М.: Дрофа,2002
2. Математика. Приложение к газете «Первое сентября». 1997. № 1, 10, 46, 48; 1998. № 8, 16, 17, 20, 21, 47.
3. Скоркина, Н.М. Нестандартные формы внеклассной работы. Для средних и старших классов/ Н.М. Скоркина.  – Волгоград: Учитель, 2004
4. Зив, Б.Г., Гольдич,В.А. Дидактические материалы по алгебре и началам анализа для 10 класса./Б.Г.Зив, В.А.Гольдич. – 3-е изд., исправленное. – СПб.: «ЧеРо-на-Неве», 2004
5. Алгебра и начала анализа: математика для техникумов/под ред. Г.Н.Яковлева.-М.: Наука, 1987