Тема урока "Вероятностный подход к определению количества информации"

Урок по предмету «Информатика и ИКТ» (10 класс)

Тема урока "Вероятностный подход к определению количества информации"

Цели урока:

·        Обучающая – формирование у учащихся понимания вероятности, равновероятных событий, не равновероятных событий; вероятностного подхода к измерению информации;

·        Развивающая – развивать умение качественно оценивать поставленную задачу для правильного выбора способа решения задачи; развивать самостоятельность; логическое мышления учащихся.

·        Воспитательная – формировать интерес к предмету, навыки контроля и самоконтроля; чувство ответственности, деловые качества учащихся.

Методическая цель: продемонстрировать использование интерактивных методов (деловой игры).

Тип урока: урок изучения и закрепления нового материала.

Оборудование: Компьютер,  операционная система Windows 7, проектор, презентация по теме «Вероятностный подход к определению количества информации»

Ход урока

1. Организационный момент.

2. Объяснение нового материала (сопровождается презентацией):

Введение понятия “количество информации”

- Можно ли измерить количество вещества и как именно?

- Можно ли определить количество энергии?

- Можно ли измерить количество информации и как это сделать?

Сегодня на уроке, мы с вами поговорим о том, как можно измерить информацию и как найти ее количество.

Для измерения информации существуют два подхода. Один из них называется содержательный или вероятностный.

Количество информации, заключенное в сообщении, определяется объемом знаний, который несет это сообщение человеку. Этот подход субъективный (зависит от конкретного человека). Разные люди, получившие одно и то же сообщение, по-разному оценивают количество информации, содержащееся в нем. Это происходит от того, что знания людей о событиях, о которых идет речь в сообщении, различны

Пример. Первоклассник изучает таблицу умножения. Учитель сообщает ему, что 2 х 2 = 4. Первоклассник этого раньше не знал, поэтому такое сообщение содержит для него информацию. А для ученика 5 класса таблица умножения хорошо известна, поэтому из такого сообщения информацию он не получит.

Рассмотрим примеры.

Допустим, вы бросаете монету, загадывая, что выпадет: орел или решка? Есть всего два варианта возможного результата бросания монеты. Причем, ни один из этих вариантов не имеет преимущества перед другим. В таком случае говорят, что они равновероятны.

Так вот, в этом случае перед подбрасыванием монеты неопределенность знаний о результате равна двум. Игральный кубик с шестью гранями может с равной вероятностью упасть на любую из них. Значит, неопределенность знаний о результате бросания кубика равна шести.

Следовательно, можно сказать так: неопределенность знаний - это количество возможных результатов события (бросания монеты, кубика; вытаскивания жребия и пр.)

Пример:

На экзамен приготовлено 20 билетов.

·        Чему равно количество событий, которые могут произойти при вытягивании билета? (20)

·        Равновероятны эти события или нет? (да)

·        Чему равна неопределенность знаний ученика перед тем как он вытянет билет? (20)

·        Во сколько раз уменьшится неопределенность знания после того как ученик билет вытянул? (20)

·        Зависит ли этот показатель от номера вытянутого билета? (нет)

Вернемся к примеру с монетой.

 Предположим, что у монеты обе стороны “орел”.

·        Существует ли неопределенность знаний перед броском в этом случае? Почему? (нет, заранее знаем, что выпадет “орел”)

·        Получите вы новую информацию после броска? (нет, ответ знаем заранее)

·        Будет ли информативным сообщение о результате броска? (не будет, поскольку оно не принесло новых и полезных знаний)

·        Чему равно количество информации в этом случае? (нулю, так как данное сообщение является неинформативным)

Информация при данном подходе рассматривается как знание для человека.

За единицу измерения информации принимается уменьшение неопределенности знаний человека в 2 раза.

Такая единица измерения является минимальной единицей информации, и называют такую единицу – битом.

Ну, а теперь давайте попробуем применить наши полученные знания в игре «Угадай число».

Игра “Угадай число”.

Один из учеников загадывает число из интервала от 1 до 16. Учитель задает вопросы, ученик на них отвечает, и весь класс вместе с учителем заполняют следующую таблицу:

Работа в парах:

Один из учеников загадывает число в интервале от 1 до 8, второй – отгадывает это число, пользуясь приведенной выше стратегией игры.

Учитель сам объявляет количество полученных бит информации – 3, а затем спрашивает у учащихся их результат.

Существует формула, которая связывает между собой количество возможных событий и количество информации.

N = 2^I, где

N — количество возможных вариантов,

I —  количество информации.

Если из этой формулы выразить количество информации, то получится I= log₂N.

Неравновероятные события.

В жизни же мы сталкиваемся не только с равновероятными событиями, но и событиями, которые имеют разную вероятность реализации.

Например:

1. Когда сообщают прогноз погоды, то сведения о том, что будет дождь, более вероятно летом, а сообщение о снеге — зимой.

2. Если вы — лучший ученик в классе, то вероятность сообщения о том, что за контрольную работу вы получили 5, больше, чем вероятность получения двойки.

3. Если в мешке лежат 20 белых шаров и 5 черных, то вероятность достать черный шар меньше, чем вероятность вытаскивания белого.

Как вычислить количество информации в таком сообщении?

Для этого необходимо использовать следующую формулу:

I = , где р - вероятность отдельного события.

Это формула Хартли.

Мы рассмотрели примеры в игровой форме, а теперь давайте попробуем решить несколько практических задач. И научимся находить количество информации, которая измеряется в битах.

3. Решение задач

1. В корзине лежат 8 мячей разного цвета (красный, синий, желтый, зеленый, оранжевый, фиолетовый, белый, коричневый). Какое количество информации несет в себе сообщение о том, что из корзины будет вынут мяч красного цвета?

Решение.

Так как возможности вынуть мяч каждого из возможных цветов равновероятны, то для определения количества информации, содержащегося в сообщении о выпадении мяча красного цвета, воспользуемся формулой I= log₂N.

Имеем I= log₂8= 3 бита.

Ответ: 3 бита.

2. В корзине лежат 8 черных шаров и 24 белых. Сколько информации несет сообщение о том, что достали черный шар?

Решение:

8+24=32 – общее количество шаров в корзине;

8/32 = 0,25 – вероятность того, что из корзины достали черный шар;

I= - log₂ 0,25 = - (-2) = 2 бита.

Ответ: 2 бита

3. В корзине лежат 32 клубка шерсти. Среди них – 4 красных. Сколько информации несет сообщение о том, что достали клубок красной шерсти?

Решение:

4/32 = 1/8 – вероятность того, что из корзины достали клубок красной шерсти;

I= - log₂ (1/8) = - (-3) = 3 бита.

Ответ: 3 бита

4. В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей было в коробке?

Решение:

Пусть в коробке было х белых карандашей.

Вероятность того, что достали белый карандаш, равна – х/64.

Количество информации сообщения о том, что достали белый шар, равно I= - log₂ (х/64) бит, что по условию задачи составляет 4 бита, т.е. имеет место уравнение:

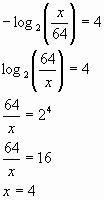
Значит, в коробке было 4 белых карандаша.

Ответ: 4 карандаша

5. В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего в корзине шаров.

Решение:

Пусть в корзине - х белых шаров

Тогда всего шаров – (х + 18).

Вероятность того, что достали белый шар равна – .

Количество информации сообщения о том, что достали белый шар, равно

I= - log₂ бит, что по условию задачи составляет 2 бита, т.е. имеет место уравнение:

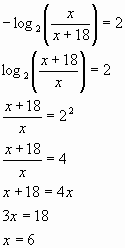
В корзине было 6 белых шаров.

Следовательно, всего в корзине – (6+18)=24 шара

Ответ: 24 шара.

4. Подведение итогов урока: оценка работы группы и обучающихся, отличившихся на уроке.

5.Домашнее задание 

1. В ящике лежат 36 красных и несколько зеленых яблок. Сообщение “Из ящика достали зеленое яблоко” несет 2 бита информации. Сколько яблок в ящике?

2. В концертном зале 270 девушек и несколько юношей. Сообщение “Первым из зала выйдет юноша” содержит 4 бита информации. Сколько юношей в зале.

3. В корзине 15 яблок, 15 груш и 30 слив. Сколько бит информации несет сообщение о том, что из корзины извлечена груша?

4. В коробке лежат 16 разноцветных фломастеров. Какое количество информации содержит сообщение, что из коробки достали фиолетовый фломастер?

Список литературы:

1.   Тихомирова Л.Ф., Басова А.В. «Развитие логического мышления детей» - Волгоград: Учитель, 2002.

2.   «Информатика», Еженедельная методическая газета для учителей информатики.

3.   Коваленко В.Г. «Дидактические игры на уроках информатики». М. Просвещение 2005г.

4.                 Интернет – ресурсы: www. 1september.ru