Тематические тестовые задания по алгебре и началам анализа для 10 класса по теме: «Показательные, логарифмические уравнения и неравенства»

Тематические тестовые задания по алгебре и началам анализа для 10 класса по теме:

«Показательные, логарифмические уравнения и неравенства»

 Калимбетова Т.И.

БОУ г. Омска «Лицей № 166»

Использование на учебных занятиях элементы тестирования помогут учителю повысить эффективность проверки успеваемости учащихся. Для школьников он полезен при отработке учебного материала и при подготовки к итоговой аттестации.

Инструкция:

1.     Тест состоит из 12 заданий.

2.     На решение задач отводится 40 минут.

3.     К каждой из 12 задач, предложенных в тесте, дается 5ответов помеченных буквами А; В; С; Д; Е. Решить задачу вы должны выбрать из них единственно верный и записать соответственную букву в таблицу результатов под номером задачи.

Таблица результатов

4.     Для решения задач НЕ ТРЕБУЕТСЯ учебник, таблицы, справочники.

5.     Не спешите, проверяйте решение.

Отметка за выполнение теста такова, что намного выгоднее не решить задачу вообще, чем решить её не верно.

Положительной отметки достоин тот, кто верно, решит не менее 9-10 задач.

Желаем успеха!

                              Тест №1 (на базовом уровне)

Вариант I

1.     Вычислить: log₂₅ 5

А) 2;                В) ½;            С);            Д) 5;              Е)

2. Вычислить: 27 ^⅓

А) 3;                В) ⅓;          С) Верный ответ не указан;    Д) 2;              Е)

3. Решить уравнение: 4^x+3 = 64

А) 4;                В) 0;              С) -3;               Д) Нет решений;           Е) 1

4. Решить уравнение: (⅓)^x = 9

A) -2;               В) ±2;            С) Нет решений;       Д) -½;               Е) ½

5. Решить уравнение: 2^5-2x = 2^3х+4

А) ⁹/_5;              В) -¹/_5;     С) Нет решений;       Д) ¹/₅;      Е) ±¹/_5;

6. Решить уравнение:

А) 0;                В) ±1;            С) 0; -1;         Д) 0; 1;                Е) Решений нет.

7.Решить уравнение: log₂ x = 3

А) -8;               В) 9;              С) 6;              Д) ²/_3;            Е) 8

8. Решить уравнение: log _x 27 = 3

А) 2;                В) -3;             С) -2;             Д) 3;              Е) Нет решений.

9. Решить уравнение: log₃ (x² – 1) = 1

А) 2;       В) -2;      С) ±2           Д) 1; 2;          Е) Верный ответ не указан.

10. Решить уравнение: log²₃ x + 2log₃ x – 15 = 0

А) ¹/_243;            В) ¹/_243; 27;    С)27;      Д) -¹/_243;       Е) Нет решений.

11. Решить неравенство: 3^х > 5

А) x < log₃ 5  В) x > ⁵/₃       C) x < ⁵/₃          Д) x = ⁵/₃         Е) x = log₃ 5

12. Решить неравенство: log_½ x > 3

A) x < ¹/₈       B) x > ¹/₈      C) x < 8      Д) 0 < x < ¹/₈               Е) x > 0

                                          Вариант II

1.     Вычислить log₇ 49

A) 2               B) -1;               С) 1; -2;         Д) 2;              Е) 0

2. Вычислить 36^½

А) 1;              В) 6;                С) 36;            Д) 0;              Е) 5

3. Решить уравнение: 5^х+7 = 25

А) 2;       В) 5;       С) -5;        Д) -¹/₅               Е) Правильный ответ не указан.

4. Решить уравнение: (¹/₆)^х+1 = 36

А) 3;              В) -3;               С) ±3;            Д) -¹/_2;              Е) Нет решений.

5. Решите уравнение: 3^1-9х = 3^х-3

А)1;       В) -1;      С) 0;         Д) ±1;            Е) Правильный ответ не указан.

6. Решить уравнение: 5 · 5^2х – 24 · 5^х – 5 = 0

А) -1;             В) ±1;              С) 1; 0;          Д) 1;              Е) 0; ±1

7. Решить уравнение: log₃ x = 2

А) 9;              В)-9;                С) 6;              Д) ±9;            Е)5

8. Решить уравнение: log _x 25 = 2

А) -5;     В)¹/_5;      С) ;      Д) 5;              Е) Правильный ответ не указан.

9. Решить уравнение: log₈₅ (x²+6) = 1

А) 3;              В) -3;               С);            Д) ¹/_3;               Е) ±3

10. Решить уравнение: log²₃ x – 6 log₃ x + 9 = 0

А) 3;       В) 27;     С) -3;        Д) 3; 27;        Е) Правильный ответ не указан.

11. Решить неравенство: 5^х > 11

А) x > ¹¹/_5;     В) x < ⁵/_11;         C) х > log₅ 11     Д) x > log₁₁ 5;         Е) х < log₅ 11

12. Решить неравенство: log_¼ x > 2

А) x < ¹/_16;      В) 0 < x < ¹/_16;  С) x > ¹/_16;            Д) x > 0;                  Е) x = ¹/₁₆

                                     Тест №2 (на профильном уровне)

Вариант I

1.     Найти область определения функции: y = log₅ (4+5x)+

А) x < 2;     В) x ≥ 2;      С) x > 2;      Д) x ≠ 2;      Е) Правильный ответ не указан.

2. Решить уравнение: 3 · 16^х + 2 · 81^х = 5 · 36^х

А) 0; ½;    В) 0;            С) ½;        Д) Нет решений.               Е) -½.

3. Решить уравнение: log₂ (4-х) + log₂ (1-2x) = 2 log₂ 3

А) -0,5;       В) 5;            С) 5; -½;    Д) Решений нет.                Е) -5; ½.

4. Решить уравнение: log (х²+2х-1) - log х = 2

А) ±1;         В) 0;       С) Правильный ответ не указан.  Д) -1;        Е) 1.

5. Вычислить: А, если А=4^В, В=0,5 log₄ 9-0,25 log₂ 25

А) 6;           В) 0,6;    С) -0,6;            Д) ²/_3;                                             Е) -6.

6. Решить уравнение: х^lgx = 1000x²

А) 100;       В) 1000; С) 1000; 0,1;    Д) 100; 0,1;                  Е) 0,1.

7. Решить уравнение: log_2x+7 (2-2x+5) = 0.5

А)4.5;         В)1;        C) 0;                Д) 1; 45;                      E) -4.5.

8. Решить уравнение: log₃ (9^x+8) = 2+х

А) 0;           В) log₃ 8;     С) 0; log₈ 3;    Д) 0; log₃ 8;               Е) log₈ 3.

9. Решить уравнение: log_х 4+ log₂ (x²) =5

А) 4;           В);         С) 1; 4;        Д) 4;;     Е) Правильный ответ не указан.

10. Решить неравенство: 4^х+2^х+1 ≥ 3

А) (0; ∞);    В) [0; ∞);    С) (-3; 1);    Д) (1; ∞);    Е) Правильный ответ не указан. 

11. Решить неравенство: log₃ (x²+ 4x+3) ≤ 1

А) (-0;4)   В) [-4;-3]  C) (-1;0);     Д) Правильный ответ не указан  Е)[-4;-3] ∪(-1;0].

12. Решить систему: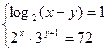

А) (0;5;4;5);              В) (0;1);      С) (1;0;)           Д) (4;5;0;5);        Е) Правильный ответ не указан.

Вариант II

1. Найти область определения функции: y=

А)   В);          С)      Д)          Е)

2. Решить уравнение:

А)           В)1;0;            С)1;          Д)0;        Е) Правильный ответ не указан.

3. Решить уравнение:

А)-5;                В) Нет решений;           С)1;        Д)-5; 1;      Е)5; 1.

4. Решить уравнение:

F)-1; 7;        В) 0;            С) 7;         Д) Правильный ответ не указан;     E) -1.

5. Вычислить:

А) 1;           В) 4;            С) 3;         Д) -4;             Е) Правильный ответ не указан.

6. Решить уравнение: =0,0001

А) 100; 10   В)0,1;         С) 100;10;0,1;0,01;        Д) 100;10;0,1;  Е) 100;10;0,01.

7. Решить уравнение:                        

А)   В);   С) 1;    Д)      Е) Правильный ответ не указан.  

8. Решить уравнение:

А) 0;              В) 3;              С) -3;   Д)            Е) Правильный ответ не указан.

9. Решить уравнение:

А)27;             В)             С) 27; ;          Д) 27; ;      Е) Решений нет.

10. Решить неравенство:

А) ; В)  С) (;-¹/₂);  Д) (1; );   Е) Правильный ответ не указан.

11. Решить неравенство:

А)      В)       С)  Д) Правильный ответ не указан; Е)

12. Решить систему: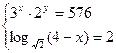

А) (6; 2);         В) (2; 6);      С) (0; 6);           Д) (6; 1);         Е) Правильный ответ не указан.

                     Как оценивать выполнение теста

Ниже приведены таблицы верных ответов к тестам №1 и №2.

Для каждого из них, сравнив свою таблицу с итоговой, подсчитайте:

Х - число примеров, решенных верно.

Y - число примеров, решенных с ошибкой.

Z – число примеров, которые вы не успели решить.

 - количество полученных баллов.

                                    отметка «5»

                                    отметка «4»

                                    отметка «3»

M<34                                     отметка «2»       

Ответы

Тест №1 (базовый уровень)

В-1

В-2

Тест №2 (профильный уровень)

В-1

В-2

Скачано с www.znanio.ru