Теорема Пифагора

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГИМНАЗИЯ №9 МОСКОВСКОГО РАЙОНА Г.КАЗАНИ

Реферат

На тему: Теорема Пифагора

                                                 Выполнил ученик 9 Б класса

                                                                                                           Карзанов Владимир                   

                                                                                                Проверила учитель математики

                                                                                    Кузнецова С.А.            

Казань  2025

Содержание

I. Введение

Основная часть

 1.История теоремы

2. Карикатура

3. Формулировки

II. Виды доказательств и практическое применение теоремы

1. Доказательство

2. Доказательство

3. Доказательство

8. Практическое применение теорема Пифагора

III. Заключение

Список используемой литературы

Цели:
1) изучить различные доказательства теоремы Пифагора.
Задачи:
1) изучить литературу по теме «Теорема Пифагора»;
2) изучить и проанализировать доказательства теоремы;

3) научиться применять математические идеи и методы в решении задач.

Задачи определили структуру работы, которая состоит из введения, основной части и заключения.

Методы изучения:

1) сбор и исследование информации;

2) самостоятельная постановка и решение исследовательской задачи.

Введение

Геометрия владеет двумя сокровищами: одно из них —
это теорема Пифагора...
Иоганн Кеплер.

      Цель моей исследовательской работы показать практическое применение теоремы Пифагора, фундаментальной теоремы, которая является основой применения численных методов геометрии.

      Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии устанавливающая соотношение между сторонами прямоугольного треугольника.  На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.

      В школьном курсе геометрии приводится доказательство теоремы методом площадей, но существуют и другие интересные доказательства, которые  я рассмотрел в своей работе. Так же я рассмотрел теорему Пифагора с точки зрения ее прикладного характера и провел свое исследование с помощью теоремы.

История теоремы

    Исторический обзор начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: "Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".  Кантор (крупнейший немецкий историк математики) считает, что равенство 3² + 4² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора  гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м и привяжем к ней по цветной полоске на расстоянии 3м от одного конца и 4 метра от другого. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.

     Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммурапи, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой - на критическом

изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод: «Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку».

      Геометрия у индусов, как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.    В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".

     Удобный и очень точный способ, употребляемый землемерами для проведения на местности перпендикулярных линий, был известен с древних времён. Этот способ, по-видимому, применявшийся ещё тысячелетия назад строителями египетских пирамид, основан на том, что каждый треугольник, стороны которого относятся как 3:4:5, согласно теореме Пифагора - прямоугольный, так как 3² + 4² = 5².

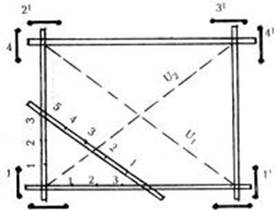
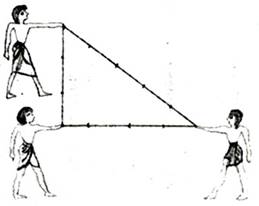                       Поэтому треугольник с катетами 3, 4 и гипотенузой 5 называют “египетским”. Прямые углы (например, для отрыва котлована) можно определять двумя способами: применяя теорему Пифагора и используя точку пересечения двух кривых. Для того чтобы воспользоваться первым методом, достаточно сбить три - тонкие доски и прямоугольный треугольник, длины сторон которого будут кратны 3, 4 и 5 м. С помощью такого треугольника легко выполнить разбивку здания на местности. Метод настолько прост, что не нуждается в дополнительных пояснениях. Точность разбивки будет зависеть от точности нанесения отметок на сторонах треугольника, то есть, от аккуратности измерения.

Карикатуры

     Доказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его Dons asinorum- ослиный мост. Слабые ученики, заучившие теоремы наизусть, без понимания, были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее также "ветряной мельницей", составляли стихи вроде "Пифагоровы штаны на все стороны равны", рисовали карикатуры.

       Теорема Пифагора - одна из главных теорем геометрии. Значение ее состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии

Формулировки

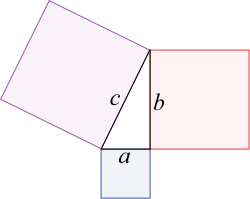
Теорема Пифагора: Сумма площадей квадратов, опирающихся на катеты a и b, равна площади квадрата, построенного на гипотенузе c.

Геометрическая формулировка:

Изначально теорема была сформулирована следующим образом:

Алгебраическая формулировка:

То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:  a² + b² = c². Обе формулировки теоремы эквивалентны, но вторая формулировка проще, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.

Доказательство №1

Случай равнобедренного прямоугольного треугольника.

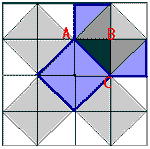Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах. Простейшее доказательство теоремы получается в случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Например, для ΔABC: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, - по два. Теорема доказана.

Доказательство №2

Через подобие треугольников.

       Следующее доказательство алгебраической формулировки наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигур.

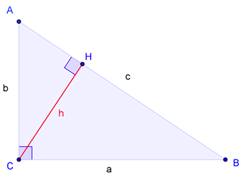
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения

получаем

Что эквивалентно

Сложив, получаем

 Теорема доказана.

Практическое применение теоремы Пифагора

        Теорема Пифагора также применяется в литературе, мобильной связи, архитектуре (индийцы, например, использовали её для построения алтарей, которые по священному предписанию должны иметь геометрическую форму, ориентированную относительно четырех сторон горизонта), а также в астрономии. В конце 19 века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. Вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать, но очевидно, что математический факт, переданный в виде теоремы  Пифагора,  имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Задачи с элементами исследования

  1) При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе R=200 км? (радиус Земли ОС равен r = 6380 км.)  Решение: Пусть АВ=х км, ВС=R=200 км,

 ОВ= r+ х .

Используя теорему Пифагора, получим  

u Ответ: 2,3 км.

  2)    У меня дома   в кухонной комнате (6 м х 6 м)  летом был сделан ремонт. На пол выложили квадратную плитку  серого цвета в виде ромбиков. Я измерил плитки и узнал, что они имеют стороны 30 см. В ходе расчетов я пришел к выводу, что если бы плитки имели стороны по 35 см, то получилось бы выгоднее. Было бы меньше отходов при распиливании плиток, их практически бы не было совсем, что с экономило бы семейный бюджет. Я произвел расчеты:

По теореме Пифагора (а² + b² = c²) я вычислил гипотенузу, прямоугольного треугольника (диагонали плитки) :           35²  + 35² =1225+1225= 2450

см +0,5 см = 50 см  (0,5 см интервал между  )

Периметр нашей кухни 24 м= 2400 см; 2400:50 = 48(шт.) - половинок по периметру кухонной комнаты.

Вывод:  Ровно 24, разрезанные по диагонали плитки  нужно приклеить по периметру кухни, при этом отходов не должно остаться.

Заключение

       В заключении еще раз хочется сказать о важности теоремы. В наши дни теорема Пифагора очень важна и актуальна. И несущественно то, что она была известна за много веков до Пифагора, важно то, что Пифагор выделил её, дополнив собственными исследованиями, повысив значимость в мире математических открытий. Теорема применяется в геометрии на каждом шагу. Из неё или с её помощью можно вывести большинство теорем геометрии. Всего известно около 367 различных доказательств теоремы Пифагора. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора продолжает оставаться живительным источником красоты, совершенства и творчества для новых и новых поколений. Несмотря на то что, суть теоремы проста и изящна, но было бы ошибкой думать, что в плане её содержания не осталось места для каких-то новых исследований. Результатом одного из таких исследований являются Пифагоровы тройки - наборы из трёх натуральных чисел, из которых сумма квадратов двух чисел равна квадрату третьего числа. Сейчас уже найдены стороны 50-го «пифабедренного» треугольника (первый, египетский со сторонами 3, 4 и 5 всем известен), значения которых очень велики. К сожалению, невозможно привести все или даже самые красивые доказательства теоремы, однако хочется надеяться, что приведенные примеры убедительно свидетельствуют об огромном интересе сегодня, да и вчера, проявляемом по отношению к теореме Пифагора. Как мы видим, история математики почти не сохранила достоверных данных о жизни Пифагора и его математической деятельности. Зато легенда сообщает даже ближайшие обстоятельства, сопровождавшие открытие теоремы.

     Тем не менее, можно сделать вывод, что теорема является основой применения численных методов геометрии.

Литература

1.Л.С.Атанасян 7-9 класс геометрия

2. https://infourok.ru/rp-po-geometrii-9-klass-7799816.html

3. https://www.kp.ru/edu/shkola/teorema-pifagora/

4.А.П. Ершова   Дидактические материалы по геометрии

Скачано с www.znanio.ru