«Теорема Пифагора в действии»  

8 класс в формате первой части ОГЭ.

 Вы можете воспользоваться ссылками выше или выполнить задания в тетрадях. Тексты заданий ₁ продублированы ниже. В случае выбора электронной версии для получения оценки достаточно отправлять скриншот результата.  

В качестве бонусного упражнения предлагаю рассмотреть вариант ВПР 2020 года.

26.12 

1) Катеты прямоугольного треугольника равны 3 и 4. Найдите гипотенузу этого треугольника. Подсказка:  

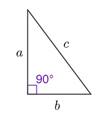 Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 

𝑐² = 𝑎² + 𝑏²

Катеты (а и в) – стороны прямоугольного треугольника, содержащие прямой

угол. Гипотенуза (с) – наибольшая сторона прямоугольного треугольника, лежащая напротив прямого угла.  

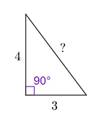Для нашей задачи запишем теорему Пифагора:  

                                                                                                                          c2 = 42 + 32                                                          2

Проведем вычисления:  

c² = 25 с  

𝑐 = ±5

Так как, с – величина, соответствующая длине гипотенузе, то она не может быть отрицательной

(с > 0). 

Ответ: с = 5.

2)   Катеты прямоугольного треугольника равны 6 и 8. Найдите гипотенузу этого треугольника.

3)   Катеты прямоугольного треугольника равны 5 и 12. Найдите гипотенузу этого треугольника.

4)   Катеты прямоугольного треугольника равны 7 и 24. Найдите гипотенузу этого треугольника.      

27.12 

1) Сторона квадрата равна  . Найдите диагональ этого квадрата.

Подсказка:  

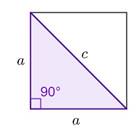Так как диагональ квадрата отсекает прямоугольный треугольник, то верна теорема Пифагора.  

𝑐² = 𝑎² + 𝑏²

Для нашей задачи запишем теорему Пифагора:  c

Проведем вычисления:  

c² = 25 ⋅ 2 + 25 ⋅ 2  c² = 100 с  

                                                                                                         𝑐 = ±10                                                                              3

Так как, с – величина, соответствующая длине гипотенузе, то она не может быть отрицательной

(с > 0). 

Ответ: с =10.

2)   Сторона квадрата равна  . Найдите диагональ этого квадрата.

3)   Сторона квадрата равна  . Найдите диагональ этого квадрата. 4) Сторона квадрата равна  . Найдите диагональ этого квадрата.

28

1) Биссектриса равностороннего треугольника равна . Найдите сторону этого треугольника.   

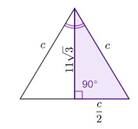Подсказка:  

В равностороннем треугольнике все стороны равны (по определению). Обозначим их c. 

По свойствам равнобедренного треугольника, биссектриса, проведенная к основанию, является медианой и высотой. А значит, в равностороннем треугольнике данным свойством обладают все биссектрисы. Тогда биссектриса отсекает прямоугольный треугольник с гипотенузой 𝑐 и одним из катетов ₂^с. Сама биссектриса становится вторым катетом и по условию равна .

Тогда, по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен ₄ сумме квадратов катетов. 

𝑐

Проведем вычисления:  

                                                                                  𝑐 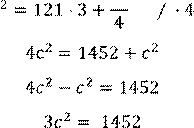𝑐2 

𝑐² = 484 с  

𝑐 = ±22

Так как, c – величина, соответствующая длине стороны равностороннего треугольника, то она не может быть отрицательной (с _{> 0}). 

Ответ: с = 22

2)    Биссектриса равностороннего треугольника равна . Найдите сторону этого

треугольника.  

3)    Биссектриса равностороннего треугольника равна . Найдите периметр этого треугольника.

4)    Высота равностороннего треугольника равна . Найдите периметр этого треугольника.

5)    Высота равностороннего треугольника равна . Найдите сторону этого треугольника.

6)    Медиана равностороннего треугольника равна . Найдите сторону этого треугольника.

                                                                                                                                                                                                                                      5

29

1) Сторона равностороннего треугольника равна . Найдите биссектрису этого треугольника. 

Подсказка:  

В равностороннем треугольнике все стороны равны (по определению). И по условию равны . 

По свойствам равнобедренного треугольника, биссектриса, проведенная к основанию, является медианой и высотой. А значит, в равностороннем треугольнике данным свойством обладают все биссектрисы. Тогда биссектриса отсекает прямоугольный треугольник с

гипотенузой  и одним из катетов . Сама биссектриса становится вторым катетом, который нам и необходимо найти.

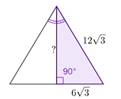
Тогда, по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен ₆ сумме квадратов катетов. 

 Проведем вычисления:  

𝑎² = 144 ⋅ 3 − 36 ⋅ 3 a² = 324

𝑎  

𝑎 = ±18

Так как, a – величина, соответствующая длине биссектрисы, то она не может быть отрицательной (𝑎 _{> 0}).  Ответ: a = 18

2)    Сторона равностороннего треугольника равна . Найдите биссектрису этого

треугольника.  

3)    Сторона равностороннего треугольника равна . Найдите биссектрису этого треугольника.

4)    Сторона равностороннего треугольника равна . Найдите высоту этого треугольника.

5)    Сторона равностороннего треугольника равна . Найдите медиану этого треугольника.

6)    Сторона равностороннего треугольника равна . Найдите медиану этого треугольника.

7

30

1)   Катеты прямоугольного треугольника равны 3 и 4. Найдите гипотенузу этого треугольника.

2)   Сторона квадрата равна  . Найдите диагональ этого квадрата.

3)   Биссектриса равностороннего треугольника равна . Найдите периметр этого треугольника.   

4)   Сторона равностороннего треугольника равна . Найдите биссектрису этого треугольника. 

8