ТЕОРЕМА ПИФАГОРА
Цели: доказать теорему Пифагора и обратную ей теорему, рассмотреть решение задач с применением этих теорем.
Ход урока
I. Проверка домашнего задания.
№ 466.
Решение
|
|
1) ВЕ – высота в равнобедренном треугольнике и медиана АЕ = ЕD = 7,6 см. 2) 3) SАВСD = (15,2 · 7,6) = 115,52 см2. |
АВЕ – прямоугольный и
равнобедренный АЕ = ВЕ = 7,6 см.Решить задачи (устно):
1. α = 3β. Найти β.
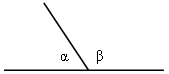
2. α + γ = β. Найти β.
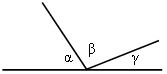
3. Найти площадь четырехугольника ВDАС.
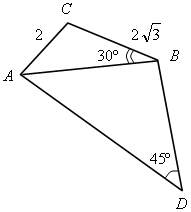
II. Изучение нового материала.
1. Доказательство теоремы провести с помощью учащихся.
2. Для закрепления теоремы можно предложить учащимся устные задачи на вычисление:
|
|
а) а = 6 см; b = 8 см. Найти: с. б) с = 5 см, b = 3 см. Найти: а. |
3. Напомнить учащимся понятие обратной теоремы. Всегда ли она верна? Разобрать вопросы из домашнего задания.
4. Сформулировать с помощью учащихся теорему, обратную теореме Пифагора.
5. Доказательство теоремы Пифагора.
6. Рассказать учащимся о том, что хотя эта теорема и связана с именем Пифагора, она была известна задолго до него.
III. Закрепление изученного материала.
Решить задачи: №№ 483 (г), 484 (а, в), 498 (в, д).
IV. Итоги урока.
|
|
1)
если 2)
если с2 = а2 + b2, то |
С = 90°, то с2
= а2 + b2;Домашнее задание: § 3, п. 54, 55, вопросы 8–10, с. 134; №№ 483 (в), 484 (б, г), 498 (б, г, ж). Существует более ста доказательств теоремы Пифагора. По желанию подготовить сообщения с 5–6 доказательствами теоремы Пифагора.
Для желающих.
1. С помощью теоремы Пифагора доказать, что в прямоугольном треугольнике любой из катетов меньше гипотенузы.
Доказательство
|
|
По теореме Пифагора АВ2 = АС2 + ВС2. Так как ВС2 > 0, то АС2 < АВ2, то есть АС < АВ. |
2. Подготовить сообщения об истории теоремы Пифагора.
ТЕОРЕМА ПИФАГОРА Цели: доказать теорему
Для закрепления теоремы можно предложить учащимся устные задачи на вычисление: а) а = 6 см; b = 8 см
Доказательство По теореме
© ООО «Знанио»
С вами с 2009 года.
