теория- Абсолютно твёрдое тело (1)

 Абсолютно твёрдое тело

Про­из­воль­ные си­сте­мы точек под дей­стви­ем внеш­них сил дви­га­ют­ся и ме­ня­ют свою форму (де­фор­ми­ру­ют­ся). Су­ще­ству­ют аб­со­лют­но твёр­дые тела, то есть тела, раз­мер и форму ко­то­рых счи­та­ют неиз­мен­ны­ми (раз­ме­ром де­фор­ма­ции пре­не­бре­га­ют). При­кла­ды­вая силы к со­во­куп­но­сти точек аб­со­лют­но твёр­до­го тела, можно при­ве­сти его в дви­же­ние и (или) к вра­ще­нию.

Сум­мой сил, дей­ству­ю­щих на аб­со­лют­но твёр­дое тело, на­зы­ва­ет­ся такая сила, ко­то­рая вы­зы­ва­ет такое же дви­же­ние этого тела, как и дей­ству­ю­щие на него силы.

 Условия равновесия абсолютно твёрдого тела

Когда сумма дей­ству­ю­щих на тело сил равна нулю, центр масс этого тела на­хо­дит­ся в со­сто­я­нии рав­но­мер­но­го пря­мо­ли­ней­но­го дви­же­ния, то есть су­ще­ству­ет такая си­сте­ма инер­ци­аль­но­го от­счё­та, в ко­то­рой центр масс этого тела по­ко­ит­ся (пер­вое усло­вие рав­но­ве­сия аб­со­лют­но твёр­до­го тела). Од­на­ко тело может вра­щать­ся от­но­си­тель­но этого цен­тра масс (см. рис. 1).

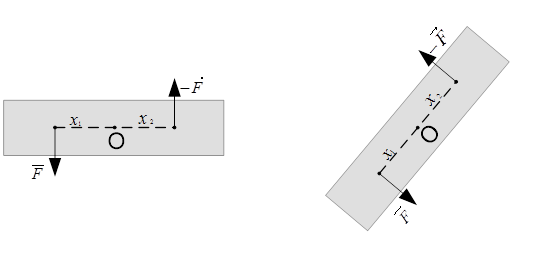
Рис. 1. Вра­ще­ние аб­со­лют­но твёр­до­го тела при ну­ле­вом зна­че­нии суммы дей­ству­ю­щих сил

От­сут­ствие вра­ща­тель­но­го дви­же­ния тела обес­пе­чит ну­ле­вое зна­че­ние суммы мо­мен­тов дей­ству­ю­щих на него сил (вто­рое усло­вие рав­но­ве­сия аб­со­лют­но твёр­до­го тела). При этом точка, от ко­то­рой от­счи­ты­ва­ют­ся мо­мен­ты, яв­ля­ет­ся про­из­воль­ной.

Мо­дуль мо­мен­та силы равен про­из­ве­де­нию плеча силы (крат­чай­шее рас­сто­я­ние от точки, от ко­то­рой от­счи­ты­ва­ют­ся мо­мен­ты, до линии дей­ствия силы) на саму силу. То есть, если вы­брать точку Oкак точку, от ко­то­рой от­счи­ты­ва­ют­ся мо­мен­ты на рис. 1, то мо­мент силы  равен про­из­ве­де­нию плеча  на эту силу, и он на­прав­лен про­тив ча­со­вой стрел­ки; мо­мент силы  – про­из­ве­де­ние плеча  на эту силу, и он также на­прав­лен про­тив ча­со­вой стрел­ки. Сле­до­ва­тель­но, в дан­ном слу­чае, сумма мо­мен­тов этих сил от­лич­на от нуля.

Если на­пра­вить силу  в про­ти­во­по­лож­ную сто­ро­ну (см. рис. 2), тогда её мо­мент на­прав­лен по ча­со­вой стрел­ке, а сумма мо­мен­тов сил  и  может быть равна нулю.

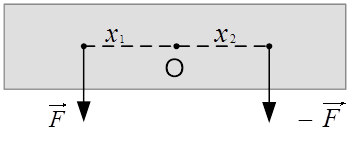
Рис. 2. Силы, дей­ству­ю­щие на твёр­дое тело

 Суммарная сила параллельных сил и точка её приложения

Сум­мар­ная сила (F) долж­на быть не толь­ко рав­ной по ве­ли­чине сумме па­рал­лель­ных сил (их можно скла­ды­вать по аб­со­лют­ной ве­ли­чине, так как они на­прав­ле­ны оди­на­ко­во), но и иметь такой же мо­мент от­но­си­тель­но любой точки, как и ис­ход­ные силы (). Для этого необ­хо­ди­мо найти такую точку, от­но­си­тель­но ко­то­рой сум­мар­ный мо­мент сил  равен нулю, то есть . И при­ло­жить в этой точке сум­мар­ную силу  (см. рис 4). Из вы­ра­же­ния  на­хо­дим ко­ор­ди­на­ту точки. Это и будет точка при­ло­же­ния сум­мар­ной силы.

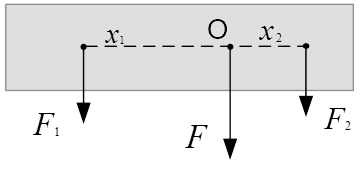
Рис. 4. Сло­же­ние па­рал­лель­ных сил

 Центр тяжести абсолютно твёрдого тела

Опре­де­ле­ние точки при­ло­же­ния сум­мар­ной силы поз­во­ля­ет уста­но­вить центр тя­же­сти твёр­до­го тела.

Центр тя­же­сти – точка при­ло­же­ния сум­мар­ной силы тя­же­сти, дей­ству­ю­щей на раз­ные ма­те­ри­аль­ные точки, со­став­ля­ю­щие дан­ную си­сте­му.

Для опре­де­ле­ния точки, к ко­то­рой при­кла­ды­ва­ет­ся сум­мар­ная сила тя­же­сти, необ­хо­ди­мо тело, изоб­ра­жён­ное на рис. 4, по­вер­нуть на про­из­воль­ный угол. При этом из­ме­нит­ся на­прав­ле­ние дей­ствия сил  (но они оста­нут­ся па­рал­лель­ны­ми), на­прав­ле­ние дей­ствия силы F. Пе­ре­се­че­ние линий дей­ствия сум­мар­ной силы F до и после из­ме­не­ния по­ло­же­ния тела ука­жет ис­ко­мую точку – центр тя­же­сти (т. O) (см. рис. 5).

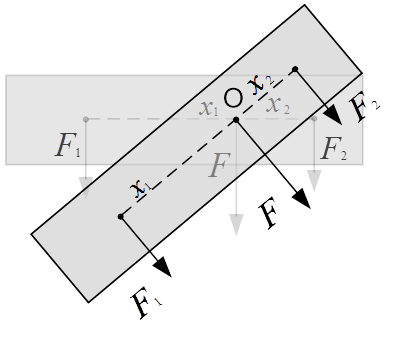
Рис. 5. Опре­де­ле­ние точки при­ло­же­ния сум­мар­ной силы тя­же­сти

 Положения равновесия

Рав­но­ве­сие твёр­до­го тела может быть устой­чи­вым или неустой­чи­вым.

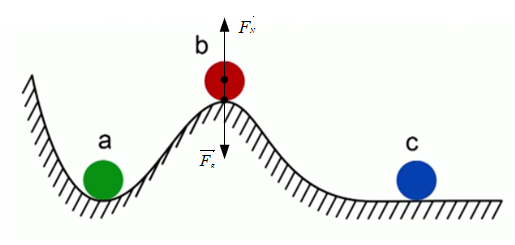
Рис. 6. По­ло­же­ния рав­но­ве­сия

На рис. 6 изоб­ра­жён шарик b, ко­то­рый лежит на горке. Сумма дей­ству­ю­щих на него сил равна нулю, если центр тя­же­сти на­хо­дит­ся на одной вер­ти­каль­ной линии с точ­кой опоры (сила ре­ак­ции опоры () дей­ству­ет снизу вверх, сила тя­же­сти (), при­ло­жен­ная к цен­тру ша­ри­ка, дей­ству­ет свер­ху вниз, их сумма и сумма их мо­мен­тов равна нулю). Но, если этот шарик вы­ве­сти из по­ло­же­ния рав­но­ве­сия, он ска­тит­ся. Такое по­ло­же­ния рав­но­ве­сия на­зы­ва­ет­ся неустой­чи­вым.

По­ло­же­ние ша­ри­ка c так же почти неустой­чи­во, так как любое без­ко­неч­но малое воз­дей­ствие на него может при­ве­сти к сдви­гу в любую сто­ро­ну. Такое по­ло­же­ние рав­но­ве­сия на­зы­ва­ет­ся без­раз­лич­ным.

Шарик a на­хо­дит­ся в устой­чи­вом по­ло­же­нии рав­но­ве­сия, так как при его сме­ще­нии от по­ло­же­ния рав­но­ве­сия воз­ни­ка­ют силы, воз­вра­ща­ю­щие в ис­ход­ное по­ло­же­ние.

Устой­чи­вое рав­но­ве­сие твёр­до­го тела – это такое рав­но­ве­сие, при ко­то­ром сумма сил, дей­ству­ю­щих на тело, и их мо­мен­тов равна нулю, и при вы­во­де этого тела из по­ло­же­ния рав­но­ве­сия воз­ни­ка­ют силы или мо­мен­ты сил, ко­то­рые воз­вра­ща­ют или по­во­ра­чи­ва­ют его в по­ло­же­ние рав­но­ве­сия.

Скачано с www.znanio.ru