Теория графов

ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ЭЛЕМЕНТОВ ТЕОРИИ ГРАФОВ

Задание 1. Аня задумала некоторое число, если к нему прибавить 23, потом полученную сумму разделить на 3, затем из частного вычесть 36, далее прибавить 6, и полученный результат умножить на 14. То получится число 112. Найти задуманное число.

Решение:

Для начала сделаем рисунок.

Рис.1. Решение задачи 1

Как мы можем заметить, чтобы найти задуманное число, необходимо выполнить действия обратные тем, что даны по условию.

Рис. 2. Решение задачи 1

Ответ задачи: Задуманное число: 112.

Задание 2. Кузнечик прыгает по 15-ти метровой тростинке. Он может прыгать либо вниз на девять метров, либо вверх на семь метров. Может ли он прыгнуть с трех до двенадцати метров?

Решение:

Так как кузнечик может либо прыгать вверх на семь, значит, будем записывать как результат сложения +7, либо вниз на 9, значит -9.

Рис.3. Решение задачи 2

На последнем шаге получаем 9 этаж, прибавить 7 мы не можем, так как будет выше, чем 15 метров, отнять 9 также мы не можем, так как получим 0.

Ответ задачи: С трех до двенадцати метров кузнечик прыгнуть не может.

Задание 3. На одной улице было расположено 9 домов. Известно, что по соседству от Павла живут Инна и Алексей, Мария является соседкой Инне и Семену, Вика – Даше и Насте, Егор – сосед Насте. Больше соседей на этой улице нет. Соседями являются те, кто имеют общий участок забора. Может ли Павел через участки попасть к Насте?

Решение:

Изобразим графически, кто является между собой соседями.

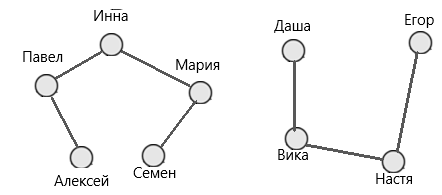
Рис.4. Решение задачи 3

Павел не сможет попасть к Насте, так как они не являются соседями.

Ответ задачи: нет, не может.             

Задание 4. В Солнечной системе имеется восемь известных планет: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран и Нептун. Между этими планетами проведено сообщение для связи. Не все планеты имеют связь между собой. Меркурий соединен с Марсом, Земля с Юпитером, Венера с Землей, Сатурн с Нептуном, Уран с Сатурном, Нептун с Марсом. Можно ли отправить сообщение через другие планеты с Сатурна в Юпитер?

Решение:

Нарисуем схему планет, и связи между ними.

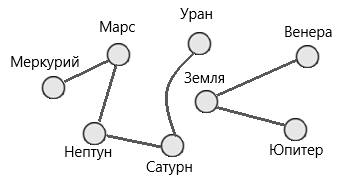
Рис.5. Решение задачи 4

По рисунку мы явно видим, что отправить сообщение между данными планетами невозможно.

Ответ задачи: нет, не может.

                Задание 5. Трое друзей, Катя, Петя и Коля. Решили вместе перекусить. Но вот начинку для бутербродов любили разную: с сыром, с колбасой и с маслом. Определите, какой бутерброд любит каждый из них, если Катя, Петя и любитель бутербродов с маслом, питаются правильно, а Петя и любитель сыра играют вместе в компьютерные игры?

Решение:

Первое множество, это множество трех друзей: Катя, Петя и Коля. Вторым множеством являются «начинки для бутербродов», то есть: сыр, колбаса и масло. Элементы данных множеств обозначим точками.

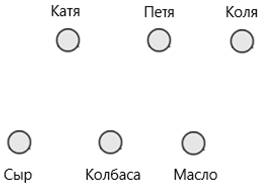
Рис.6. Решение задачи 5

Если условие является верным, то соединяем точку первого множества с точкой второго множества сплошной красной линией. Если же условие не может быть выполнено, то соединяем пунктирной линией. Исходя из условия задачи, каждому из друзей предполагается только один выбор из второго множества.

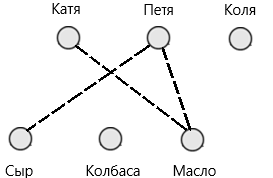
Рис. 7. Решение задачи 5

                Делаем вывод о том, что если какая-либо точка первого множества соединена двумя пунктирными линиями с двумя точками второго множества, то с третьей точкой она соединяется сплошной линией. Следовательно, следующий шаг будет выглядеть следующим образом:

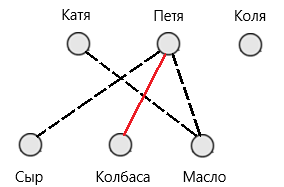
Рис. 8. Решение задачи 5

                По условию известно что: «Катя, Петя и любитель бутербродов с маслом, питаются правильно», а это значит, что Коля и есть тот, кто любит бутерброды с маслом. Мы установили, что Петя любит бутерброды с колбасой, Коля с маслом. Следовательно, Катя любит бутерброды с сыром.

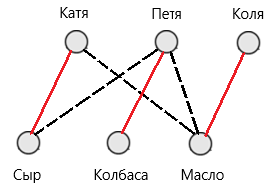
Рис.9. Решение задачи 5

Ответ задачи: Катя любит бутерброды с сыром, Петя любит бутерброды с колбасой, Коля любит бутерброды с маслом.

                Задание 6. В кинокружке «Эпизод» собрались трое любителей различных жанров фильмов такие как: комедии, мелодрамы и триллеры. Первый участник говорит: «Вы какие больше фильмы любите? Я люблю комедии!». Другой ответил, что любит мелодрамы, а третий сказал, что обожает триллеры. Интересно, что все они были в кепках и футболках синего, зеленого и красного цветов, но цвет кепки и футболки совпадал только у любителя комедий. У любителя мелодрам ни кепка, ни футболка, не были зеленого цвета. Любитель триллеров был в красной футболке. Определите цвет кепок и футболок каждого участника кинокружка.

Решение:

Для начала сделаем схематическую запись, поскольку нам необходимо определить цвет кепки и футболки каждого из любителей фильмом, то всего будет три множества. Первое множество: жанры фильмов, второе множество возможный цвет, третье множество, это кепка или футболка.

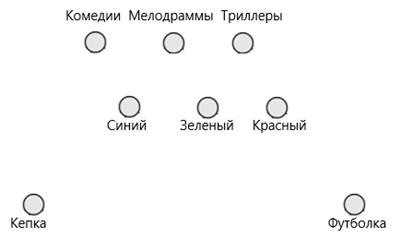
Рис. 10. Решение задачи 6

                Далее, по условию задачи известно, что: «У любителя мелодрам ни кепка, ни футболка, не были зеленого цвета», значит, мы можем пунктирной линией нарисовать данное условие. Следующее что мы знаем, что: «Любитель триллеров был в красной футболке», для удобства проведем это условие красной линией.

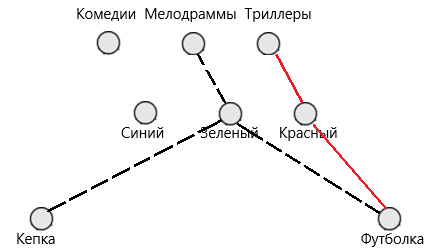
Рис. 11. Решение задачи 6

Таким образом, мы понимаем, что любитель мелодрам, ни в зеленой, и ни в красной футболке, значит, он в синей футболке. И для любителя комедий остается зеленая футболка.

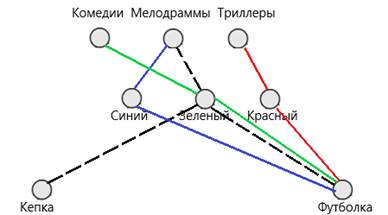
Рис.12. Решение задачи 6

Теперь мы определились с цветом футболки у каждого, переходим к кепкам. Мы знаем, что: «цвет кепки и футболки совпадал только у любителя комедий», значит у любителя комедий зеленая кепка. Значит у двух других участников цвет кепки и футболки совпадать не может.

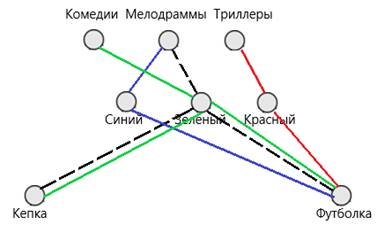
Рис. 13. Решение задачи 6

Ответ задачи: У любителя комедий, кепка и футболка зеленого цветов. У любителя мелодрам, синяя футболка и красная кепка. У любителя триллеров, красная футболка и синяя кепка.