
Содержание
Введение
Глава 1. История теории групп
Глава 2. Основные определения теории групп
2.1 Примеры групп
2.2 Порождающие множества элементов
2.3 Теорема Лагранжа
2.4 Классы сопряженных элементов
2.5 Инвариантные подгруппы. Гомоморфизмы групп
2.6 Прямое произведение групп
2.7 Теорема Кэли
2.8 Точечные группы симметрии
Глава 3. Некоторые физические приложения теории групп
3.1Влияние симметрии на физические свойства кристаллов
3.2 Нормальные колебания симметричных молекул
3.3 Применение теории групп к вычислению матричных элементов
Заключение
Список использованной литературы
Актуальность темы исследования. Симметрия, гармония – это наиболее общие понятия, идеи, выработанные в процессе познания человечеством окружающего мира и своего места в нем. Они включают повторяемость событий во времени и в пространстве, сохранение свойств объектов при различных преобразованиях, движениях и, в конечном счете, сами законы природы. Эти идеи и понятия нашли воплощение в самых разных сторонах деятельности людей – науке, искусстве, ремеслах. Достаточно отметить математические формулировки множества единообразных объектов, повторяемость узоров орнаментов при трансляциях, поворотах, отражениях, ритмичность работы машин и т.п. Наиболее четким математическим отображением идеи симметрии служит теория групп, имеющая дело с самыми различными множествами преобразований. Подробно о развитии идеи симметрии и ее математическом оформлении, различных проявлениях симметрии и ее нарушений в природе и искусстве рассказал выдающийся математик Г. Вейль в своем последнем труде – лекциях о симметрии (Вейль Г. Симметрия. М.: Наука, 1968).
Самым известным приложением теории групп в доквантовой физике является описание симметрии кристаллов. К 1830 году, когда возник математический термин «группа», относится и вывод Гесселем 32-х кристаллографических классов. Вывод Федоровым и Шенфлисом в 1891 году 230 пространственных групп считается шедевром анализа. Но в XIX-м веке физическая и математическая ветви теории групп развивались практически независимо друг от друга. Широкое внедрение группового аппарата в физику началось вскоре после создания квантовой механики и связано оно с именами Г. Вейля, Е. Вигнера, Г. Бете, Ю. Рака и многих других известных математиков и физиков.
Возможности применения теории групп сильно расширились в связи с тем, что состояния в квантовой механике, в отличие от классической, задаются векторами в абстрактном гильбертовом пространстве, а преобразования симметрии представляются унитарными (или анти-унитарными) преобразованиями этого пространства. Было выявлено, что группа симметрии квантово-механической системы и ее неприводимые представления могут быть использованы для классификации энергетического спектра и стационарных состояний системы, вычислений матричных элементов и расчетов по теории возмущений. Представление гамильтониана в виде суммы последовательно убывающих членов, учитывающих все более тонкие взаимодействия в системе, на языке теории групп означает постепенное понижение симметрии, переход от исходной группы высокой симметрии к ее подгруппам. При таком подходе оказывается возможным проследить за генеалогией уровней энергии системы и ее стационарных состояний, и он широко используется в теории атомных и ядерных спектров, спектров молекул и твердых тел. Без больших изменений его можно использовать для рассмотрения спектров других наблюдаемых величин. В теории спектров элементарных частиц решается скорее обратная задача: по имеющимся спектрам (или их кусочкам) угадать симметрию, объединяющую различные частицы. Потребности физики стимулировали развитие целого ряда крупных направлений математической теории групп, таких как канонические формы неприводимых представлений различных групп, теория коэффициентов Клебша Гордона, унитарные представления некомпактных групп Ли, различные расширения групп Пуанкаре. Первые значительные результаты в этих направлениях были получены как раз физиками.
Как видно, для успешного применения идей симметрии помимо знакомства с общими понятиями теории групп и их представлений необходимо достаточно подробно знать часто встречающиеся в физике конкретные группы симметрии. В число последних входят группы, описывающие «геометрию» систем: группа вращений в трехмерном пространстве, лежащая в основе атомной спектроскопии, различные ее конечные подгруппы («точечные группы симметрии»), описывающие внешнюю симметрию молекул и кристаллов, группа перестановок одинаковых частиц. Особое место в этом ряду занимает симметрия относительно обращения времени, привносящая в физику анти-унитарные преобразования.
Схема практического использования теории групп во многих задачах довольно проста: описание симметрии системы, составление приводимого представления на множестве состояний системы, рассматриваемых в данной задаче, разложение его на неприводимые составляющие с помощью операторов проектирования и, при необходимости, расчеты матричных элементов на полученных проектированием симметричных состояниях.
Целью данной выпускной квалификационной работы является изучения теории группы и некоторых ее приложений.
Для достижения данной цели необходимо выполнить ряд следующих задач:
- рассмотреть историю возникновения и развития теории групп;
- раскрыть основные определения теории групп;
- привести примеры физических приложений теории групп.
Объектом выпускной квалификационной работы является теория групп и ее приложения.
Предметом исследования является общая теория групп.
Структура выпускной квалификационной работы состоит из введения, трех глав, заключения и списка использованной литературы.
Понятие группы возникло в 18 веке оно исходит из нескольких дисциплин: теории решения алгебраических уравнений в радикалах (в трудах Ж. Лагранжа и А. Вандермонда в 1771 г. впервые для нужд этой теории были применены подстановки и было получено разложение группы подстановок на смежные классы, в 19 в. глубокие связи между свойствами группы подстановок и свойствами уравнений были указаны Н.Абелем в 1824 г. и Э. Галуа в 1830 г. Особенно нужно отметить достижения Э.Галуа в теории групп. Он открыл роль нормальных подгрупп в решении задачи о разрешимости уравнений в радикалах, установил простоту знакопеременных групп степени выше четырех. К. Жордан систематизировал и развил исследования в этом направлении в трактате о группе подстановок в 1870 г.). В проективной геометрии независимо от этого группы возникают, когда изучается поведение фигур при различных преобразованиях, что перешло на изучение самих преобразований и поиск их классификации (здесь можно назвать имена А. Мебиуса, исследовавшего элементарные виды родства геометрических фигур, А. Кэли, пришедшего к пониманию группы как системы, заданной порождающими элементами и соотношениями, Ф. Клейна – создателя в 1872 г. «Эрлангенской программы», положившей в основу классификации геометрий понятие группы преобразований) [3, c. 15].
Теоретико-групповые идеи прослеживаются и в теории чисел. Л. Эйлер в 1761 г. при изучении «вычетов, остающихся при делении степеней» пользовался сравнениями и разбиениями на классы вычетов, т. е. на смежные классы по подгруппе. К. Гаусс в 1801 г. в «Арифметических исследованиях» определил подгруппы группы Галуа уравнения деления круга и при изучении «композиции двоичных квадратичных форм» доказал, что классы эквивалентных форм образуют относительно композиции конечную абелеву группу.
В конце 19 в. выработалось современное абстрактное понятие группы. В 1895 г. С. Ли уже определял группу как совокупность преобразований, замкнутую относительно операции, которая ассоциативна и гарантирует единицу и обратные элементы.
Изучение групп без предположения их конечности и без предположений о природе элементов оформилось в самостоятельную область математики в 1916 г. в книге «Абстрактная теория групп» нашего соотечественника О.Ю. Шмидта.
В настоящее время теория групп является одной из самых развитых областей алгебры, имеющей многочисленные приложения как в самой математике, так и за ее пределами — в топологии, теории функций, кристаллографии, квантовой механике и других областях математики и естествознания.
Теория групп — раздел общей алгебры, изучающий алгебраические структуры, называемые группами, и их свойства. Группа является центральным понятием в общей алгебре, так как многие важные алгебраические структуры, такие как кольца, поля, векторные пространства, являются группами с расширенным набором операций и аксиом. Группы возникают во всех областях математики, и методы теории групп оказывают сильное влияние на многие разделы алгебры [10, c. 28].
В процессе развития теории групп построен мощный инструментарий, во многом определивший специфику общей алгебры в целом, сформирован собственный глоссарий, элементы которого активно заимствуются смежными разделами математики и приложениями. Наиболее развитые ветви теории групп — линейные алгебраические группы и группы Ли — стали самостоятельными областями математики. Различные физические системы, такие как кристаллы или атом водорода, обладают симметриями, которые можно смоделировать группами симметрии, таким образом находя важные применения теории групп и тесно связанной с ней теории представлений в физике и химии.
Одним из наиболее значительных математических прорывов XX века стала полная классификация простых конечных групп — результат совместных усилий многих математиков, занимающий более 10 тыс. печатных страниц, основной массив которых опубликован с 1960 по 1980 годы.
У теории групп три исторических корня: теория алгебраических уравнений, теория чисел и геометрия. Математики, стоящие у истоков теории групп, — это Леонард Эйлер, Карл Фридрих Гаусс, Жозеф Луи Лагранж, Нильс Хенрик Абель и Эварист Галуа. Галуа был первым математиком, связавшим теорию групп с другой ветвью абстрактной алгебры — теорией полей, разработав теорию, ныне называемую теорией Галуа.
Одной из первых задач, приведших к возникновению теории групп, была задача получения уравнения степени m, которое имело бы корнями m корней данного уравнения степени n (m \textless n). Эту задачу в простых случаях рассмотрел Худде (1659 г.). В 1740 г.
Сондерсон заметил, что нахождение квадратичных множителей биквадратных выражений сводится к решению уравнения 6 степени, а Ле Сёр (1748 г.) и Вейринг (с 1762 по 1782 гг.) развили эту идею. Общую основу для теории уравнений, строящуюся на теории перестановок, в 1770—1771 гг. нашёл Лагранж, и на этой почве в дальнейшем выросла теория подстановок. Он обнаружил, что корни всех резольвент, с которыми он сталкивался, являются рациональными функциями от корней соответствующих уравнений. Чтобы изучить свойства этих функций, он разработал «исчисление сочетаний» (Calcul des Combinaisons) [9, c. 27].
Современная ему работа Вандермонда (1770 г.) также предвосхищала развитие теории групп. Паоло Руффини в 1799 г. предложил доказательство неразрешимости уравнений пятой и высших степеней в радикалах. Для доказательства он использовал понятия теории групп, хоть и называл их другими именами. Руффини также опубликовал письмо, написанное ему Аббати, лейтмотивом которого была теория групп. Галуа обнаружил, что если у алгебраического уравнения несколько корней, то всегда существует группа перестановок этих корней такая, что
1. всякая функция, инвариантная относительно подстановок группы, рациональна и, наоборот,
2. всякая рациональная функция от корней инвариантна относительно перестановок группы. Свои первые труды по теории групп он опубликовал в 1829 г., в возрасте 18 лет, но они остались практически незамеченными, пока в 1846 г. не было издано собрание его сочинений.
Артур Кэли и Огюстен Луи Коши стали одними из первых математиков, оценивших важность теории групп. Эти учёные также доказали некоторые важные теоремы теории. Изучаемый ими предмет был популяризован Серретом, который посвятил теории секцию из своей книги по алгебре, Жорданом, чей труд «Действия над подстановками» (Traité des Substitutions) стал классикой, и Ойгеном Нетто (1882 год).
Большой вклад в развитие теории групп внесли также многие другие математики XIX века: Бертран, Эрмит, Фробениус, Кронекер и Матьё. Современное определение понятия «группа» было дано только в 1882 г. Вальтером фон Дюком. В 1884 г. Софус Ли положил начало изучению как групп преобразований того, что мы сейчас называем группами Ли и их дискретными подгруппами; за его трудами последовали работы Киллинга, Штуди, Шура, Маурера и Эли Картана [16, c. 115].
Теория дискретных групп была разработана Клейном, Ли, Пуанкаре и Пикаром в связи с изучением модулярных форм и других объектов. В середине XX века (в основном, между 1955 и 1983 гг.) была проведена огромная работа по классификации всех конечных простых групп, включающая десятки тысяч страниц статей. Ощутимый вклад в теорию групп внесли и многие другие математики, такие как Артин, Эмми Нётер, Людвиг Силов и другие.
В настоящее время теория групп представляет собой хорошо развитую область математики. Каждый год проходят международные конференции, посвященные теории конечных и бесконечных групп. Только в России в 2017 г. прошло несколько международных конференций по теории групп.
Хорошо развитые школы, занимающиеся теорией групп, имеются в Москве, Санкт-Петербурге, Екатеринбурге, Новосибирске, Омске, Томске, Иркутске, Челябинске, Красноярске и других городах России. Сотни специалистов высшей квалификации занимаются различными разделами теории групп.
В России регулярно выходят журналы «Алгебра и логика», «Сибирский математический журнал», «Фундаментальная и прикладная математика», «Дискретная математика», «Доклады академии наук», в которых большую долю занимают статьи по теории групп. Российскими учеными написаны десятки монографий по конечным и бесконечным группам. Достижения российских специалистов по теории групп давно и заслуженно признаны во всем мире.
Группа – множество G, на котором определена бинарная групповая операция («умножение»), сопоставляющая каждой паре элементов a, b Î G определенный элемент c Î G, ab = c. Умножение подчиняется аксиомам (1) ассоциативности (ab)c = a(bc); (2) в группе имеется единичный элемент e Î G, ae = ea = a; (3) для каждого элемента a Î G существует обратный ему элемент a-1 Î G, aa-1 = a-1a = e. Группа называется абелевой (коммутативной), если для любых a, bÎ G имеет место ab = ba. Множество H Ì G называется подгруппой группы G, если оно замкнуто относительно заданной на G операции умножения [17, c. 40].
В зависимости от числа элементов множества G (точнее, от его мощности) различают группы конечные, бесконечные дискретные, непрерывные и смешанные непрерывные. Число элементов конечной группы называют ее порядком. Элементы бесконечной дискретной группы можно перенумеровать с помощью натурального ряда чисел или любого счетного множества символов. Элементы непрерывной группы задаются посредством конечного числа непрерывно меняющихся параметров. Группа называется компактной, если ее параметры пробегают ограниченные интервалы значений. В смешанных группах некоторые параметры пробегают дискретный (в частности, конечный) набор значений.
Группой является совокупность элементов линейного пространства Ln со сложением векторов в качестве групповой операции (в частности, множество всех вещественных чисел, комплексных чисел). Роль единицы группы играет нулевой вектор, обратный элемент для вектора a – противоположный вектор -a. Группа абелева, непрерывная n-параметрическая (2n в комплексном случае), некомпактная.
GL(n, R) [GL(n, C )] – группа всех неособенных линейных операторов (матриц) в вещественном (R) или комплексном (C ) пространстве Ln с умножением операторов в качестве групповой операции. Группа некоммутативна (если n ¹ 1), непрерывная n2-параметрическая (2n2 в комплексном случае), некомпактная. Унитарная группа U(n) – подгруппа GL(n, C ) – определяется n2 независимыми параметрами; группа компактная. Унитарная унимодулярная группа SU(n) Ì U(n) (матрицы с определителем 1) – (n2-1)-параметрическая [19, c. 72].
Группа вращений в трехмерном
евклидовом пространстве SO (3, R) (другие обозначения O![]() , R3 ) –
непрерывная трехпараметрическая компактная группа; одна из возможных
параметризаций – с помощью трех углов Эйлера. Полная ортогональная группа в
трех измерениях O (3, R) (или О3) служит примером смешанной группы –
три непрерывных параметра (углы Эйлера) дополняются четвертым параметром,
принимающим два значения (скажем, + и -) и различающим собственные и
несобственные вращения.
, R3 ) –
непрерывная трехпараметрическая компактная группа; одна из возможных
параметризаций – с помощью трех углов Эйлера. Полная ортогональная группа в
трех измерениях O (3, R) (или О3) служит примером смешанной группы –
три непрерывных параметра (углы Эйлера) дополняются четвертым параметром,
принимающим два значения (скажем, + и -) и различающим собственные и
несобственные вращения.
Группа движений евклидова пространства – совокупность преобразований, не меняющих расстояния между любыми двумя точками; помимо вращений включает параллельные переносы точек.
Группа трансляций бесконечной кристаллической решетки – бесконечная дискретная абелева группа. В качестве элементов группы можно рассматривать векторы трансляций a(m, n, k) = ma1 + na2 + ka3, где m, n, k – любые целые числа; a1, a2, a3 определяют элементарные трансляции, параллелепипед, построенный на них, является элементарной ячейкой кристалла.
Симметрическая группа n-ой степени Pn – группа всех перестановок n объектов (чисел) – конечная группа порядка n! Произведение двух перестановок – результат последовательного проведения этих перестановок (в порядке справа налево):
![]()
![]() =
= ![]()
Перестановки можно записывать в одну строчку, в виде произведения независимых циклов: рядом с каждым числом в цикле ставится то число, на место которого переходит первое; цикл замыкается числом, переходящим на место числа, открывающего цикл. Например,
![]()
Число объектов в цикле называется его длиной, циклы длины 1, как правило, не выписываются. Перестановка, затрагивающая только два числа, называется транспозицией; она представляется одним циклом длины два. Запись перестановок неоднозначна: в полной записи можно как угодно переставлять столбцы, циклы можно начинать с любого из содержащихся в нем чисел, независимые циклы можно переставлять. Переход к обратному элементу достигается перестановкой рядов в двухрядной записи. Всякую перестановку можно представить в виде произведения транспозиций (задача 24). Число множителей в таком произведении определяет четность перестановки. Подгруппа Pn, составленная только из четных перестановок, называется знакопеременной группой An. [17, c. 55]
Важную роль в различных приложениях
играют так называемые точечные группы симметрии – группы само-совмещений
конечных геометрических фигур. Они являются подгруппами ортогональной группы
О3. Так, группа n-го порядка Cn состоит из поворотов около некоторой оси на
углы, кратные 2p/n.
В качестве объекта с такой симметрией можно представить себе коническую
шестеренку с n наклонными зубцами. Группа симметрии правильной треугольной
пирамиды, C3v, содержит шесть элементов: единичный Е, поворот C3
на 120о (для определенности против часовой стрелки, считая ось
направленной от основания к вершине пирамиды), поворот ![]() на 240о (равносильный
повороту на 120о по часовой стрелке), отражения s (1),
s (2),
s (3)
относительно плоскостей, проходящих через высоту и вершины 1, 2, 3 основания
пирамиды (нумерация, для определенности, против часовой стрелки, см. рис.).
на 240о (равносильный
повороту на 120о по часовой стрелке), отражения s (1),
s (2),
s (3)
относительно плоскостей, проходящих через высоту и вершины 1, 2, 3 основания
пирамиды (нумерация, для определенности, против часовой стрелки, см. рис.).
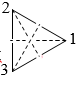
Рис. 1.
Целые степени любого элемента группы определяются следующим образом:
An =aa...a (n раз),a-n=a-1a-1...a-1,a0 = e .
Очевидно при этом, что an am = an+m , и множество {an} образует подгруппу, называемую циклической подгруппой, порожденной элементом a. Порядок циклической подгруппы называют также порядком элемента a – это наименьшая степень, при возведении в которую элемента a получается единица: ar = e. Так, циклическая группа Cn образована элементом n-го порядка Cn. [7, c. 34]
В общем случае некоторое множество элементов группы {x1, x2, …, xr} называется порождающим множеством, или системой образующих группы, если произвольный элемент группы может быть представлен в виде произведения g = xi xj …, составленного из элементов этого множества и обратных к ним. Об- разующие элементы группы связаны множеством соотношений вида xi xj … = xk xl …. Определяющими соотношениями группы называют минимальную совокупность таких соотношений, из которых все остальные можно получить в качестве следствия.
В группе C3v наименьшее порождающее множество состоит из двух элементов, например, C3, s (1) связанных определяющими соотношениями
C3 = E, s(1)2 = E, s(1)C = C 2s(1).
Пусть Н подгруппа группы G, а – произвольный элемент группы. Множество аН = {ah; h Î H} называется левым смежным классом группы G по подгруппе H, образованным элементом а. Смежный класс содержит столько же элементов, что и подгруппа; если а Ï Н, то все элементы класса отличны от элементов подгруппы, тогда как hH = H для любого h Ï H. Очевидно, в качестве «образующего» может выступать любой элемент класса, aH = ahH. Если в группе остался элемент b, не содержащийся ни в Н, ни в аН, можно образовать класс bH, не имеющий общих элементов с Н и аН и т.д. В результате группа представляется в виде объединения непересекающихся смежных классов [10, c. 52]:
G = H + aH + bH + …
Число слагаемых в этой «сумме» (r) называется индексом подгруппы Н в груп- пе G. Для конечной группы порядка n и подгруппы Н порядка m мы получаем соотношение n = mr и теорему Лагранжа: порядок подгруппы является дели- телем порядка группы.
В группе C3v подгруппа C3 обладает индексом 2, а три отражения составляют смежный класс по этой подгруппе.
Элементы группы a и b называются сопряженными друг другу, если в группе найдется элемент g такой что a = gbg-1. Множество сопряженных друг другу элементов группы образует класс, и группа может быть представлена как объединение непересекающихся классов сопряженных элементов. Порядки сопряженных элементов совпадают, единичный элемент группы сам по себе образует класс, в абелевых группах любой элемент сам по себе образует класс сопряженных элементов.
Элементом, сопряженным к повороту в группе (или подгруппе) движений евклидова пространства, является поворот на такой же по величине угол n около оси, получаемой из исходной оси в результате преобразования, осуществляющего сопряжение [17, c. 22]:
gR(n,j)g -1 = R(gˆn, ± j) (см. рис.).
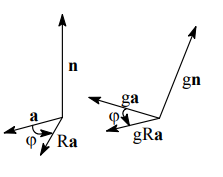
Рис. 2.
Угол поворота в правой части
равенства берется со знаком «-», если преобразование gˆ меняет правый
винт на левый. Аналогично, сопряженным к отражению в плоскости элементом
является также отражение, трансляции сопряжена трансляция на такой же по
величине вектор и т.д., т.е., сопряженные пространственные преобразования
однотипны. Напротив, два однотипных пре- образования сопряжены друг другу, если
в группе имеется преобразование, переводящее соответствующие элементы симметрии
(оси, плоскости) друг в друга. Так, в группе C3v повороты С3,
![]() сопряжены, поскольку
отражение (любое из трех) переводит ось вращения в себя, но меняет направление
поворота. Три отражения сопряжены друг другу, так как их плоскости переводятся
друг в друга поворотами (или отражениями в другой плоскости) [5,
c. 27].
сопряжены, поскольку
отражение (любое из трех) переводит ось вращения в себя, но меняет направление
поворота. Три отражения сопряжены друг другу, так как их плоскости переводятся
друг в друга поворотами (или отражениями в другой плоскости) [5,
c. 27].
Сопряженным к перестановке элементом является перестановка с той же циклической структурой. В полной группе перестановок Pn для любых двух элементов с одинаковой циклической структурой найдется перестановка, со прягающая их:
(а1a2…ai)
(ai+1…aj)…=g(b1b2…bi)bi+1…bj)…g-1,
g =![]()
так что общее число классов сопряженных элементов определяется числом возможных циклических структур для перестановок данной степени.
Подгруппа H′ = gHg-1 называется сопряженной с подгруппой H. Если H′ = H для всех g Î G, подгруппа H называется инвариантной (нормальным делителем группы G). Простые группы не имеют нетривиальных (H ¹ e, G) нормальных делителей. Полупростые группы не имеют абелевых нормальных делителей. Правые и левые смежные классы группы по инвариантной подгруппе совпадают: aH = Ha. Отсюда вытекает, что произведения элементов двух та- ких классов aH, bH (взятых в определенном порядке) все входят в один и тот же класс abH, что позволяет на множестве классов определить операцию группового умножения aH × bH = abH. В результате множество классов становится группой, G/H, называемой фактор-группой группы G по инвариантной под-группе H. Пример: подгруппа C3 в группе C3v инвариантна, два смежных класса по этой подгруппе образуют фактор-группу второго порядка [11, c. 75].
Две группы G и G* изоморфны, если между их элементами можно установить взаимно-однозначное соответствие g « g*, сохраняющее операцию умножения: (ab)* = a*b*. Изоморфное отображение группы на себя называется автоморфиз- мом; например, a* = gag-1 (внутренний автоморфизм). Более общим является понятие гомоморфизма групп; группа G гомоморфна на группу G*, G ® G*, если между элементами этих групп можно установить соответствие g ® g* (однозначное в одном направлении), сохраняющее операцию умножения, (ab)* = a*b*.
Элемент g* называют образом g, а g – прообразом g*. Нетрудно убедиться, что при гомоморфизме (и изоморфизме) единичный элемент отображается на единичный, а обратный элемент – на обратный к его образу, a-1 ® (a*)-1. Множество N Ì G прообразов единичного элемента e* группы G* называется ядром гомо- морфизма G ® G*. Основная теорема о гомоморфизме: ядро N гомоморфизма G ® G* является инвариантной подгруппой группы G, а фактор-группа G/N изо- морфна G*. Для доказательства достаточно убедиться в том, что любой элемент смежного класса aN отображается на один и тот же элемент a*.
Пример гомоморфизма группы GL(n): Aˆ ® det Aˆ (отображение на мультипликативное множество всех чисел, отличных от нуля); ядро гомоморфизма – группа SL(n). [17, c. 22]
Прямое произведение можно формально определить для любых двух (и более) групп G и G′ как множество пар G ´ G′ = { (g, g′) } со следующим законом группового умножения: (a, a′)(b, b′) = (ab, a′b′ ). Разбиение прямого произведения групп на классы сопряженных элементов предопределяется соответствующим разбиением перемножаемых групп: если {a} – класс группы G, {a′} – класс группы G′, то множество пар { (a, a′) } является классом G ´ G′. Множества пар { (g, e′ ) }, { (e, g′ ) } являются инвариантными подгруппами G ´ G′, изоморфными, соответственно, G и G′. Любая пара элементов этих подгрупп коммутирует, а любой элемент всей группы однозначно представляется в виде произведения элементов подгрупп: (a, a′) = (a, e′ )(e, a′ ) = (e, a′ )(a, e′ ). Таким образом, всякая группа, содержащая две (и более) подгруппы с указанными свойствами, может рассматриваться как прямое произведение этих подгрупп. Например, C6 = C3 ´ C2, O3 = O3+ ´ Ci, где Ci – группа инверсии [4, c. 90].
2.7 Теорема Кэли
 |
Короче структура может быть задана системой образующих и определяющими соотношениями между ними. Любой элемент группы простого порядка обязательно имеет тот же порядок, т.е., такая группа может быть только циклической. Группа четвертого порядка помимо циклической может обладать структурой, в которой все неединичные элементы – второго порядка (четверная группа типа С2 ´ С2). Группы шестого порядка могут иметь две различные структуры: циклическую и структуру группы С3v. [10, c. 37]
Из таблицы умножения
группы вытекает, что в результате умножения эле- ментов группы, расположенных в
определенном порядке [верхняя строчка таблицы – (а1, а2,…, аn)], слева на какой
либо элемент группы a получается строчка (aa1, aa2,…, aan), в которой те же
элементы расположены в другом порядке (переставлены). Таким образом, каждому
элементу группы сопоставляется перестановка n предметов: a
® ![]()
причем нетрудно убедиться в том, что произведению элементов группы отвечает произведение соответствующих перестановок. Сказанное формулируется как теорема Кэли: всякая группа порядка n изоморфна некоторой подгруппе симметрической группы n-й степени Pn. Эти подгруппы содержат только «правильные» перестановки, представляемые в виде произведения независимых циклов одинаковой длины.
Элементами точечной симметрии могут быть ось симметрии, плоскость симметрии, центр симметрии. Порядок оси – наибольший из порядков поворотов, совершаемых около этой оси. Зеркальный поворот – комбинация поворота с отражением в плоскости, перпендикулярной оси поворота: S(j) = C(j)sh = shC(j). Отражение в плоскости и инверсия являются частными случаями зеркальных поворотов: S1 = sh, S2 = C2sh = I. Отметим, что произведение двух зеркальных поворотов является чистым поворотом, произведение зеркального поворота на поворот является зеркальным поворотом. В частности, svsv′ = C(2j) – поворот около линии пересечения плоскостей v′ и v, j – угол между плоскостями, отсчитываемый от плоскости v′. Отсюда можно получить и результат умножения поворота на отражение в плоскости, проходящей через ось поворота [19, c. 28]:
sv = C(2j)sv′. Кроме того, svC(j)sv = C(-j), с примером такого соотношения мы уже сталкивались при рассмотрении группы C3v. Когда повороты около оси на противоположные углы сопряжены друг другу, ось называют двусторонней.
Перечислим возможные точечные группы симметрии:
1. Циклические группы Сn (в пределе C¥); объекты с такой симметрией обладают лишь одной осью n-го порядка.
2. Циклические группы S2n (зеркально-поворотная ось четного порядка). Частный случай – группа инверсии S2 (другoе обозначениe: Ci ).
3. Абелевы группы Cnh = Cn ´ Cs. Элементы симметрии – ось n-го порядка, плоскость отражения, а при n четном и центр симметрии. При n нечетном группа циклическая, с образующей Sn = Cnsh. Частный случай C1h º Cs.
4. Группы симметрии правильных n-угольных пирамид Cnv. Элементы симметрии – ось n-го порядка и n плоскостей, проходящих через ось и отстоящих друг от друга на углы, кратные p/n. При n > 2 группа неабелева; каждая пара взаимно-обратных поворотов образует класс сопряженных элементов; при нечетном n все отражения входят в один класс, а при n четном они разбиваются на два класса по n/2 отражений в плоскостях, связанных друг с другом поворотами Cn.
5. Группы Dn содержат в дополнение к группе Cn повороты на 180o около n осей второго порядка, перпендикулярных к «главной» оси и расположенных под углами p/n друг к другу. Группы Dn и Cnv изоморфны.
6. Группы симметрии правильных n-угольных призм Dnh = Dn * C1h. Элементы симметрии – ось n-го порядка, n перпендикулярных ей осей второго порядка, n плоскостей отражения, проходящих через главную ось и одну из осей второго порядка, плоскость отражения, содержащая оси второго порядка, при n четном имеется также центр симметрии. Число классов сопряженных элементов вдвое больше, чем в группе Dn.
7. Группы Dnd получаются в результате добавления к осям симметрии группы Dn n плоскостей, проходящих через главную ось и биссектрисы углов между соседними осями второго порядка. Нетрудно убедиться в том, что произведение отражения в плоскости и поворота на угол p около оси, расположенной под углом j к плоскости есть зеркальный поворот на угол 2j около главной оси. Таким образом, элементы симметрии здесь такие: зеркально- поворотная ось 2n-го порядка, n эквивалентных друг другу (вне зависимости от четности n) осей второго порядка, n эквивалентных плоскостей, а при n нечет- ном еще и центр симметрии. Симметрией Dnd обладает, например, фигура, полученная из двух одинаковых правильных n-угольных призм, сложенных основаниями, поворотом одной из них около общей оси на угол p /n [7, c. 25].
8. Группы симметрии правильных многогранников – тетраэдра (T, Td), октаэдра (куба) (O, Oh = O ´ Ci), икосаэдра (додекаэдра) (Y, Yh = Y ´ Ci). Группы T, O, Y содержат только поворотные элементы. Укажем классы сопряженных элементов некоторых групп (число элементов класса и типичный элемент): T (E, 4C3, 4C32, 3C2), Td (E, 8C3, 3C2, 6S4, 6sd), O (E, 8C3, 3C42, 6C4, 6C2), Oh (E, 8C32, 3C42, 6C4, 6C2, I, 8S6, 3sh, 6S4, 6sd), Y(E, 12C5, 12C52, 20C3, 15C2). От- метим, что оси третьего порядка в группе Т односторонние, а в группе Td двусторонние из-за наличия отражений в плоскостях, проходящих через эти оси. Группы Td и O изоморфны. В кристаллографии приходится встречаться еще с группой Th = T ´ Ci.
Число точечных кристаллографических групп ограничено 32-мя. Это всевозможные подгруппы групп Oh и D6h, и их таблицы умножения, таким образом, содержатся в таблицах умножения групп Oh и D6h.
Макроскопические свойства кристаллов определяются тензорами различных рангов в трехмерном пространстве: скалярами (плотность, температура и т.п.), векторами (неиндуцированная электрическая поляризация), тензорами второго ранга (диэлектрическая проницаемость, электропроводность, теплопроводность), третьего ранга (пьезоэлектрические модули), четвертого ранга (модули упругости) и т.д.
Если провести с кристаллом эксперимент, затем осуществить поворот (или зеркальный поворот) образца из точечной группы кристалла К (т.е., кристаллического класса, см. раздел 6) и повторить эксперимент, то результат эксперимента не изменится. Это можно сформулировать в виде принципа Неймана: группа симметрии любого физического свойства кристалла включает точечную группу К этого кристалла [12, c. 27].
Тензор
r-го ранга ![]() под действием элементов
группы К преобразуется согласно приводимому представлению Гv*
Гv *…* Гv =
под действием элементов
группы К преобразуется согласно приводимому представлению Гv*
Гv *…* Гv = ![]() где Гv –
трехмерное векторное представление группы, и пусть разложение на НП имеет вид:
где Гv –
трехмерное векторное представление группы, и пусть разложение на НП имеет вид:
![]() =N1
Г1+N2Г2+…
=N1
Г1+N2Г2+…
где Г1 – тождественное (инвариантное)
представление. Инвариантность тензора относительно преобразования из группы К
означает, что он лежит в N1-мерном подпространстве, на
котором осуществляется НП Г1. Иными словами, инвариантный тензор
имеет N1 линейно независимых компонент. Математический
аппарат, развитый в предыдущих разделах, позволяет найти как число N1,
так и сами инвариантные тензоры путем проектирования с помощью операторов P(1)=![]()
Часто для установления связей между компонентами тензора явно используются условия инвариантности тензора:
![]()
которые расписываются по компонентам с использованием наиболее удобных систем координат.
Рассмотрим для примера кубический кристалл с K=O, Гv =
Г4 (трехмерное НП группы октаэдра), ![]() т.е., тензор второго ранга имеет
лишь один кубический инвариант:
т.е., тензор второго ранга имеет
лишь один кубический инвариант:
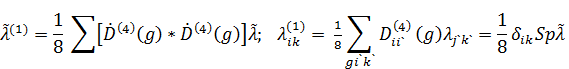
Здесь мы воспользовались соотношением ортогональности матричных элементов НП. Если тензор обладает той или иной симметрией относительно перестановок индексов, то для получения разложения оказываются полезными формулы вида:
[(Ga + Gb)2] = [Ga2] + [G 2] + Ga ´ Gb,
вытекающие
из соотношений. Так, тензор модулей упругости ![]() , определяемый
соотношением F = 1/2 ålijkmuijukm (F – свободная энергия, uij
– тензор деформаций), симметричен по первой и второй парам индексов, а также
относительно перестановок этих пар. Поэтому компоненты этого тензора
преобразуются по представлению группы вращений
, определяемый
соотношением F = 1/2 ålijkmuijukm (F – свободная энергия, uij
– тензор деформаций), симметричен по первой и второй парам индексов, а также
относительно перестановок этих пар. Поэтому компоненты этого тензора
преобразуются по представлению группы вращений
[[D(1)2] ´ [D(1)2]] = [(D(2) + D(0))2] = [D(2)2] + D(2) + D(0) = D(4) + 2D(2) + 2D(0)
Здесь мы использовали также соотношение
[D( j)2] = D(2j) + D(2j - 2) + D(2j - 4) +…,
которое можно получить, например, рассматривая симметрию соответствующих коэффициентов Клебша-Гордона. Таким образом, существует два независимых инвариантных относительно всех вращений (в том числе и несобственных) тензора. Базисные тензоры четвертого ранга:
ei ej ek el º eij ekl º eijkl.
Симметричные тензоры второго ранга, расщепленные как D(2) + D(0):
exx + eyy + ezz; (2ezz - exx - eyy) / Ö3, exx - eyy, exy + eyx, exz + ezx, eyz + ezy.
Изотропные тензоры l:
1) (exx + eyy + ezz)(exx + eyy + ezz) =
= exxxx + eyyyy + ezzzz + exxyy + eyyxx + ezzxx + exxzz + eyyzz + ezzyy,
2) 1/3 (2ezz - exx - eyy)(2ezz - exx - eyy) +
+ (exx - eyy)(exx - eyy) + (exy + eyx)(exy + eyx) + … =
= 4 /3(exxxx + eyyyy + ezzzz) - 2 /3(exxyy + eyyxx + ezzxx + exxzz + eyyzz + ezzyy) +
+ (exyxy + eyxxy + exyyx + eyxyx + exzxz + exzzx + ezxxz + ezxzx + eyzyz + ezyyz + eyzzy + ezyzy).
С понижением симметрии число инвариантов (или независимых компонент тензора) возрастает. Например, для кубических систем появляется еще один инвариант, поскольку D(4) содержит единичное представление группы Oh. Инвариантный полином несложно найти проектированием:
![]() (35z4 – 30z2r2 + 3r4 ) =
(35z4 – 30z2r2 + 3r4 ) = ![]() D(g)P ~ x4 + y4 + z4 – (3/5)r4.
D(g)P ~ x4 + y4 + z4 – (3/5)r4.
Проектируемый полином инвариантен относительно подгруппы D4h с осью четвертого порядка вдоль z, и удобно при суммировании по группе расположить элементы в порядке, соответствующем разбиению на смежные классы по подгруппе:
Oh=D4h+C4h+![]() D4h
D4h
Инвариантному полиному соответствует полностью симметричный тензор:
2(exxxx + eyyyy + ezzzz) - (exxyy + eyyxx + ezzxx + exxzz + eyyzz + ezzyy) -
(exyxy + eyxxy + exyyx + eyxyx + exzxz + exzzx + ezxxz + ezxzx + eyzyz + ezyyz + eyzzy + ezyzy),
ортогональный полученным выше изотропным тензорам. В качестве трех независимых кубически-инвариантных тензоров можно также выбрать следующие более простые:
exxxx + eyyyy + ezzzz, exxyy + exxzz + eyyxx + eyyzz + ezzxx + ezzyy,
exyxy + eyxxy + exyyx + eyxyx + exzxz + ezxxz + exzzx + ezxzx + eyzyz + ezyyz + eyzzy + ezyzy,
однако в них не выделены изотропные части.
3.2 Нормальные колебания симметричных молекул
Рассмотрим малые колебания механических систем (молекул), состоящих из n частиц (атомов). Геометрия молекулы в каждый момент времени характеризуется вектором r в 3n-мерном «пространстве смещений» – совокупностью смещений всех атомов из положений равновесия: r = (r1, r2, …, rn). Естествен- ные координаты системы – совокупность декартовых компонент смещений ri, соответствующий базис (X1, Y1, Z1, …), так что
r= å(xi Xi + yiYi + ziZi ) º å xia Xia.
i=1 ia
Здесь a = 1, 2, 3 соответствуют x, y, z-координатам. При преобразованиях сим- метрии молекулы смещение r переходит в некоторое другое возможное смещение той же молекулы, r′ = D(g)r. В (ортогональном) представлении Г, g ® D(g), выделяются инвариантные части, соответствующие поступательному и вращательному движению молекулы, так что Г = Гпост + Гвр + Гкол. [8, c. 52]
Энергия системы
H= T+V=![]()
![]()
где Tˆ и Vˆ – симметричные операторы, соответствующие положительно-определенным квадратичным формам T и V. Невырожденным линейным преобразованием
H приводится к диагональному виду
H=![]()
Здесь ql – нормальные координаты. Движение системы, при котором отлична от нуля только координата ql, называется нормальным колебанием с собственной частотой wl. Если к частоте w относятся r разных колебаний, она называется r-кратной частотой, а соответствующие колебания вырожденными.
Преобразование в общем случае (если не все массы одинаковы) неортогонально, но преобразование от приведенных координат
![]() ортогонально, ибо оно сохраняет квадратичную форму
ортогонально, ибо оно сохраняет квадратичную форму

Если задать скалярное произведение соотношением
(Х`ia
, X`jβ) = δia,jβ,
то ![]() собственный
вектор оператора V, относящийся к собственному значению
собственный
вектор оператора V, относящийся к собственному значению ![]() . [8, c. 60]
. [8, c. 60]
Три
вектора, описывающие смещение молекулы как целой вдоль направлений .
x,y,z: Qa (пост)![]()
![]() Ортогональность
вектора смещения
Ортогональность
вектора смещения ![]() векторам Qа
означает, что при таком смещении центр тяжести молекулы остается на месте:
векторам Qа
означает, что при таком смещении центр тяжести молекулы остается на месте:
![]()
Вектор
смещения, соответствующий вращению молекулы около направления Ω на
(малый) угол | Ω |: ![]() , где радиус-вектор Ri
определяет равновесное положение i-го атома относительно центра вращения,
который целесообразно совместить с центром тяжести молекулы.
Ортогональность
, где радиус-вектор Ri
определяет равновесное положение i-го атома относительно центра вращения,
который целесообразно совместить с центром тяжести молекулы.
Ортогональность
![]()
означает, что при смещении р не возникает момент импульса молекулы.
Молекулу
со смещением ![]() можно рассматривать как
результат поворота g всей молекулы с исходным смещением р. Это действие
эквивалентно изменению системы координат и не вызывает изменения энергии
системы, так что
можно рассматривать как
результат поворота g всей молекулы с исходным смещением р. Это действие
эквивалентно изменению системы координат и не вызывает изменения энергии
системы, так что ![]() , и
, и ![]()
Отсюда вытекает соотношение
![]()
т.е., нормальные координаты, связанные друг с другом преобразованиями симметрии, относятся к одной частоте. Можно сказать и так: преобразования Dˆ (g) связывают друг с другом лишь координаты, относящиеся к одной и той же частоте. Таким образом, пространство смещений молекулы расщепляется на инвариантные относительно Dˆ (g) подпространства, каждое из которых соответствует колебаниям с определенной частотой wi. Это означает разложение Гколеб:
Гкол = Ga(w1) + Gb(w2) + …
Индуцированные представления Г(wi), как правило, неприводимы; приводимость Г(wi) означала бы возможность дальнейшего расщепления, Г(wi) = Г′(wi) 6 Г′′(wi), и ее можно было бы трактовать как случайное вырождение колебаний из двух или более подпространств, не связанных преобразованиями Dˆ (g). [8, c. 70]
Соотношение говорит о том, что каждую частоту нормальных колебаний и соответствующие этой частоте нормальные координаты можно классифицировать индексом НП группы симметрии молекулы. Проведя разложение, можно предсказать число различных (отвлекаясь от возможности случайного вырождения) частот, их тип (НП) и кратность вырождения (размерность НП). Фактическое разложение Гкол позволяет указать форму колебаний типа Га, если Га входит в Гкол только один раз. В противном случае процедура проектирования, используемая при таком разложении, позволяет получить лишь так называемые координаты симметрии – смеси однотипных колебаний.
Для установления числа различных частот системы (типов нормальных колебаний) вычислим характеры представлений Г, Гкол. Если атом с i-го места под действием операции симметрии переходит на j-ое место, то D(g)ri = rj, где ri – смещение системы, при котором из положения равновесия выведен только i-ый атом. Поэтому диагональные матричные элементы в естественном базисе отличны от нуля только для тех Xia, которые отвечают атомам, остающимся на месте. Отсюда для поворота на угол j около некоторой оси и зеркального поворота получим, соответственно [8, c. 72]:
cГ(C(j)) = NC (1 + 2cosj), cГ(S(j)) = NS (-1 + 2cosj),
где NC и NS – число атомов, остающихся на местах при этих преобразованиях. Характер представления Gпост:
cпост(С(j)) = 1 + 2соsj, cпост(S(j)) = -1 + 2соsj.
Базис (ненормированный) этого представления: ![]() . Базис
представления Гвр состоит из трех аксиальных векторов
. Базис
представления Гвр состоит из трех аксиальных векторов ![]() – три
независимых вектора поворота. Характер представления Гвр:
– три
независимых вектора поворота. Характер представления Гвр:
cвр(С(j)) = 1 + 2соsj, cвр(S(j)) = 1 - 2соsj.
Отметим, что для линейных молекул представление Гвр двумерно, и в характерах следует опустить 1. Сравнивая, получаем характер колебательного представления
cкол(С(j)) = (NC - 2)(1 + 2соsj), cкол(S(j)) = NS(-1 + 2соsj).
В частности, cкол(I) = -3NI, cкол(s) = Ns (число атомов в плоскости отражения).
Отметим, что все представления и величины в этой задаче вещественны, поэтому встречающиеся при разложениях невещественные НП необходимо брать в паре с сопряженными НП, частоты колебаний для таких НП совпадают. При разложении полезно учесть, что молекула представляется в виде «слоев» эквивалентных атомов, сохраняющихся при преобразованиях симметрии, так что
G = åGk, где индекс k нумерует слои.
Пример – октаэдрическая молекула XY6, mX = M, mY = m, системы координат для всех атомов выберем идентичными
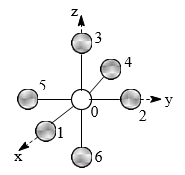
Рис. 3.
Группа симметрии системы Oh = O ´ Сi (характеры см. в приложении 2). Пространство смещений 21-мерно, характеры представлений Гпост,
Гвр и Гкол, вычисленные по формулам (4.10) – (4.12)
|
E 8C3 3 |
6C4 |
I |
8S6 |
3s |
6sd |
6S4 |
||||
|
cпост |
3 |
0 |
-1 |
-1 |
1 |
-3 |
0 |
1 |
1 |
-1 |
|
cвр |
3 |
0 |
-1 |
-1 |
1 |
3 |
0 |
-1 |
-1 |
1 |
|
cкол |
15 |
0 |
-1 |
1 |
1 |
-3 |
0 |
5 |
3 |
-1 |
Отсюда Гпост = Г4u, Гвр = Г4g, Гкол = Г1g + Г3g + Г5g + 2Г4u + Г5u (здесь индекс g означает четное по отношению к инверсии неприводимое представление группы Oh, u – нечетное). Поступательному и вращательному движению в (4.6) со- ответствуют нулевые частоты. Кроме того, имеются шесть типов нормальных колебаний. Координаты симметрии (канонический базис), находим проектированием, причем полезно обратить внимание на следующее. Пусть ищется смещение, соответствующее четному НП Гag = Гa(O) ´ Г1(Ci):
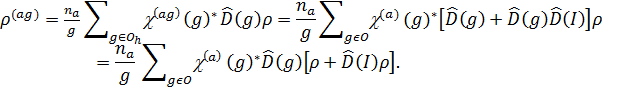
Таким образом, для нахождения четного (нечетного) относительно инверсии неприводимого смещения достаточно проектировать произвольное четное (нечетное) смещение оператором проектирования для подгруппы О.
Для НП, содержащихся в Гкол по одному разу, координаты симметрии уже являются нормальными координатами. Поэтому в приводимом ниже наборе все координаты, за исключением тех, которые соответствуют Г4u, являются нормальными [7, c. 66]:
![]() ;
;
![]()
![]()
![]()
![]()
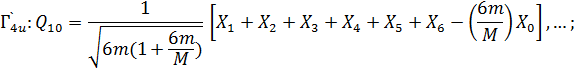
![]()
![]()
![]()
![]()
![]()
Недостающие координаты
представлений Г4u получаются из Q7, Q10, Q16 заменой в них X на Y и Z. При
операциях g ![]() O координаты симметрии
Qa(Г3) преобразуются как 3z2 - r2,Ö3 (x2 -
y2),
Qa(G4)
как x, y, z и Qa(G5)
как yz, xz, xy.
Разбиение на слои выглядит здесь как G =
GX +
GY.
Из GX µ
G4u и
поступательного смещения слоя Y6 скомбинированы координаты представлений G4u
(пост) и G‘4u.
O координаты симметрии
Qa(Г3) преобразуются как 3z2 - r2,Ö3 (x2 -
y2),
Qa(G4)
как x, y, z и Qa(G5)
как yz, xz, xy.
Разбиение на слои выглядит здесь как G =
GX +
GY.
Из GX µ
G4u и
поступательного смещения слоя Y6 скомбинированы координаты представлений G4u
(пост) и G‘4u.
Матрица упругих постоянных V на базисных векторах Qa диагональна за исключением блока, соответствующего представлениям Г4u. Этот блок, согласно и свойству симметричности, имеет вид
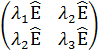
где E – единичная матрица третьего порядка, l1 = (Q7, VQ7) = …, l2= (Q7, VQ10) = …
Частоты нормальных колебаний ![]() находятся диагонализацией матрицы
находятся диагонализацией матрицы
![]() и эта же процедура обеспечивает
коэффициенты
и эта же процедура обеспечивает
коэффициенты ![]() ,
, ![]() ,
выражающие истинные нормальные координаты через координаты симметрии
,
выражающие истинные нормальные координаты через координаты симметрии ![]() Частоты остальных нормальных
колебаний задаются непосредствeнно элементами матрицы V. Например, w2(G1g)
= (Q1, VQ1),
и, подставляя сюда выражение Q1 через Xia из (4.15), находим связь w2(G1g)
с упругими постоянными kia,
jb =
(Xia, VXjb).
Частоты остальных нормальных
колебаний задаются непосредствeнно элементами матрицы V. Например, w2(G1g)
= (Q1, VQ1),
и, подставляя сюда выражение Q1 через Xia из (4.15), находим связь w2(G1g)
с упругими постоянными kia,
jb =
(Xia, VXjb).
Инвариантность матрицы V и ортогональность матриц D(g) приводят к соотношениям между различными матричными элементами: kia, jb = (D(g)Xia, VD(g)Xjb). Отметим аналогию с предыдущим параграфом: тензор второго ранга kia, jb на 3n-мерном пространстве смещений преобразуется по представлению[Г2] = N1Г1 + … группы симметрии, содержит N1 инвариантов группы, или независимых компонент тензора. Например, октаэдрическая молекула ХY6 имеет 11 несвязанных преобразованиями симметрии компонент [8, c. 74]:
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Остальные компоненты равны нулю. На упругие постоянные накладываются еще 4 условия, связанные с выделением поступательного и вращательного движений: (Q16, VQ16) = (Q7, VQ16) = (Q10, VQ16) = (Q21, VQ21) = 0. Или, после некоторых упрощений:
![]()
![]()
![]()
![]()
Частоты колебаний и параметры l:
![]() ,
,
![]() ,
,
![]()
![]() ;
;
![]()
![]()
![]()
В молекулах с осевой симметрией представление Гk, соответствующее слою k, расщепляется на две части: Гk = Гkz + Гkxy, Гkz осуществляется смещениями атомов слоя вдоль оси симметрии z, а Гkxy – смещениями в перпендикулярной к z плоскости xy. Более того, «плоские» смещения атомов слоя в направлении линии, соединяющей атом с осью, при преобразованиях симметрии также переходят в аналогичные смещения других атомов слоя. В связи с этим может оказаться удобным использовать индивидуальные системы координат (xy) для атомов, в которых ось x направлена от оси симметрии, а ось y – перпендикулярно к этому направлению. Тогда Гkxy = Гkx + Гky. Поступательные координаты всей молекулы комбинируются из поступательных координат слоев, а вращательные – из поступательных и вращательных координат слоев [17, c. 57].
Характеры Гka для отдельных слоев весьма простые. Так, слой атомов, занимающих общие положения (не на элементах симметрии) содержит g атомов, где g – порядок группы симметрии. Для такого слоя каждое представление Гka совпадает с регулярным.
Рассмотрим молекулу NH3 с симметрией C3v Обозначим M массу атома N, m – массу H, ось z для всех атомов направлена вдоль оси С3, оси x, y для атомов Н выбраны в соответствии со сказанным выше и указаны на рис.
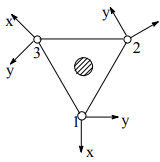
Рис.4.
x0 || x1, y0 || y1. Имеем два слоя: N (1 атом) и Н (3 атома). Характеры и разложения представлений Гka очевидны
ГHz = Г1(Hz)(Z0),
ГHxy = Г3(H)(X0,-X0/2+(![]() )Y0,
)Y0,
ГHz = Г1(Hz)(Z1 + Z2 + Z3) + Г3(Hz)(2Z1 - Z2 - Z3, 2Z2 - Z3 - Z1), ГHx = Г1(Hx)(X1 + X2 + X3) + Г3(Hx)(2X1 - X2 - X3, 2X2 - X3 - X1), ГHy = Г2(Hy)(Y1 + Y2 + Y3) + Г3(Hy)(Y2 - Y3, Y3 - Y1).
В скобках указаны базисные векторы НП (ненормированные), причем для каждого НП Г3 пара базисных векторов преобразуется подобно двум неортогональным векторам на плоскости, расположенным под углом 120о. Из Г1(N) и Г1(Hz) комбинируется одно «поступательное» представление Г1(пост.) с координатой Q7 = Z0 + Z1 + Z2 + Z3 и одно колебательное Г1 с Q1 = (3m/M)Z0 - Z1 - Z2 - Z3.
Г1(Hx) –
колебательное представление ![]()
представление G2 c Q10 = Y1 + Y2 + Y3 – врощательное (поворот молекулы около оси z). Из Г3(Hx) и Г3(Hy) комбинируется поступательное смещение слоя Н в плоскости xy:
![]()
Где колебательное представление Г3:
![]()
![]()
В Q3 атом 2 смещается перпендикулярно стороне 12 треугольника, атом 3 – навстречу ему перпендикулярно стороне 13; величины смещений всех атомов равны. Далее из Г3N и Г3(пост.Н) комбинируется представление, соответствующее поступательному смещению всей молекулы:
![]()
![]()
и ортогональная комбинация (промежуточная):
![]()
![]()
Наконец, из Г3(Hz) и Г3(пром.) комбинируем Г3(вращ.) и второе колебательное Г3:
![]()
![]()
где a – расстояние от оси до атома Н, h0 – расстояние от центра тяжести молекулы до плоскости атомов Н. Q11 соответствует повороту около оси, проходящей через центр тяжести параллельно y1, Q12 – около оси, параллельной y2.
![]()
![]()
Матрица упругих постоянных в координатах Q1 – Q6 имеет вид
V= 
Диагонализация ее сводится к решению двух квадратных уравнений, в результате чего получаются частоты двух полносимметричных невырожденных колебаний типа Г1 и двух двукратно вырожденных колебаний типа Г3 [13, c. 110].
3.3 Применение теории групп к вычислению матричных элементов
Определим
неприводимые тензорные операторы ![]() , i =
1, 2, …, na:
, i =
1, 2, …, na:
![]()
(запись преобразования операторов в форме ![]() устанавливает
связь представлений g
устанавливает
связь представлений g ![]() и g
и g ![]() на
пространстве операторов и пространстве функций, соответственно). Разложение
произвольного оператора на неприводимые части аналогичн. Матричные элементы
неприводимых тензорных операторов на стационарных состояниях:
на
пространстве операторов и пространстве функций, соответственно). Разложение
произвольного оператора на неприводимые части аналогичн. Матричные элементы
неприводимых тензорных операторов на стационарных состояниях:
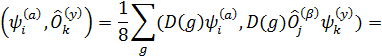
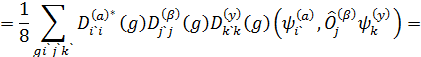
Нo![]()
где ![]() – приведенная
форма матриц представления
– приведенная
форма матриц представления ![]() . Поэтому (
. Поэтому (![]()

Правила отбора: матричный элемент отличен от нуля только в
том случае, если ![]() или
или ![]() *
*![]() . Отличные от нуля матричные
элементы можно записать в виде:
. Отличные от нуля матричные
элементы можно записать в виде:
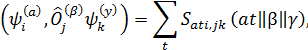
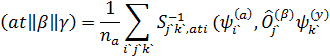
Величины (at||b||g), t = 1, 2, …, Na называют приведенными матричными эле- ментами. Коэффициенты Клебша-Гордона (группы G) – матричные элементы S, S-1. Теорема Вигнера-Эккарта [3] утверждает: зависимость матричных элементов (4.21) от индексов строчек НП полностью определяется коэффициентами Клебша-Гордона, т.е., симметрией гамильтониана. Приведенные матричные элементы можно найти, вычисляя Na обычных матричных элементов и решая систему относительно (at||b||g). Теорема Вигнера-Эккарта чаще всего используется для группы вращений.
Заключение
Теория групп, начиная с конца XIX века, оказала огромное влияние на развитие математического анализа, геометрии, механики и, наконец, физики. Оно впоследствии проникло в другие области математики - появились группы Ли в теории дифференциальных уравнений, группы Клейна в геометрии. Возникли также группы Галилея в механике и группы Лоренца в теории относительности. Произошло это всё благодаря универсальности этого понятия.
Ведь из каких бы «предметов» ни состояла группа: из чисел, движений или операций, - все они могут рассматриваться как абстрактные элементы, не обладающие никакими специфическими признаками. Для того чтобы определить группу, надо только сформулировать общие правила, которые должны выполняться для того, чтобы данную совокупность «предметов» можно было назвать группой. В настоящее время математики называют такие правила групповыми аксиомами. Тогда мы получаем, что теория групп состоит в перечислении всех логических следствий из этих аксиом.
При этом последовательно обнаруживаются все новые и новые свойства; доказывая их, математик все более и более углубляет теорию. Существенно, что ни сами предметы, ни операции над ними никак не конкретизируются. Если после этого при изучении какой-нибудь частной задачи приходится рассмотреть некоторые специальные математические или физические объекты, образующие группу, то, исходя из общей теории, можно предвидеть их свойства.
Теория групп, таким образом, дает ощутимую экономию в средствах; кроме того, она открывает новые возможности применения математики в исследовательской работе.
Введение понятия группы избавило математиков от обременительной обязанности рассматривать множество различных теорий. Оказалось, что нужно лишь выделить «основные черты» той или иной теории, и так как, по сути дела, все они совершенно аналогичны, то достаточно обозначить их одним и тем же словом, и сразу становится ясно, что бессмысленно изучать их по отдельности. Особую полезность абстрактное понятие группы получает благодаря свойству гомоморфизм, т.е. такой связи между различными группами, при котором групповая операция сохраняется. Гомоморфизм группы различной природы имеют одинаковые свойства, и изучение одной группе можно заменить изучением другой.
Например, группа поворотов трехмерного тела гомоморфную группе специальных ортогональных матриц 3×3, групповой операцией которой является умножение матриц. В большой мере именно благодаря гомоморфизмам теория групп нашла широкое применение в различных областях математики и физики, поскольку позволяет выделить общие черты в объектах очень разной природы. В настоящий момент теория групп является важной частью более глобальной области науки - «общей алгебры». В теории групп в настоящий момент много перспективных направлений, которые активно развиваются учеными всего мира.
1. Абрагам А., Блини Б. Электронный парамагнитный резонанс переходных металлов. Т. 2. М.: Мир, 1973. 351 с.
2. Барут А., Рончка Р. Теория представлений групп и ее приложения. Т. 1, 2. М.: Мир, 1980.
3. Бир Г. Л., Пикус Г. Е. Симметрия и деформационные эффекты в полупроводниках. М.: Наука, 1972. 584 с.
4. Вейль Г. Теория групп и квантовая механика. М.: Наука, 1986. 496 с. Вейль Г. Симметрия. М.: Наука, 1968. 192 с.
5. Вигнер Е. Теория групп и ее приложения к квантомеханической теории атом- ных спектров. М.: ИИЛ, 1961. 444 с.
6. Гельфанд И. М., Минлос Р. А., Шапиро З. Я. Представления группы вращений и группы Лоренца, их применения. М.: Физматгиз, Москва, 1958. 367 с.
7. Горенстейн Д. Конечные простые группы (введение в их классификацию). М.: Мир, 1985. 352 с.
8. Изюмов Ю. А., Сыромятников В. Н. Фазовые переходы и симметрия кристаллов. М.: Наука, 1984. 245 с.
9. Каргаполов М. И., Мерзляков Ю. И. Основы теории групп. Изд. 5-е. СПб.: Лань, 2009. 288 с
10. Ковалев О. В. Неприводимые и индуцированные представления и копредставления федоровских групп. М.: Наука, 1986. 368 с.
11. Курош А. Г. Теория групп. Изд. 4-е. СПб.: Лань, 2005. 648 с
12. Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). Изд. 6-е. М.: Физматлит, 2008. 800 с.
13. Ландау Л. Д., Лифшиц Е. М. Теория упругости. Изд. 5-е. М.: Физматлит, 2007. 264 с.
14. Любарский Г. Я. Теория групп и ее применение в физике: курс лекций для физиков-теоретиков. М.: URSS, Ленанд, 2014. 360 с.
15. Ляпин Е. С., Айзенштат А. Я., Лесохин М. М. Упражнения по теории групп. Изд. 2-е. СПб.: Лань, 2010. 272 с.
16. Най Дж. Физические свойства кристаллов и их описание при помощи тензоров и матриц. М.: Мир, 1967. 388 с.
17. Наймарк М. А. Теория представлений групп. Изд. 2-е. М.: Физматлит, 2010. 572 с. Эллиот Дж., Добер П. Симметрия в физике. Т. 1, 2. М.: Мир, 1983.
18. Нокс Р., Голд А. Симметрия в твердом теле. М.: Наука, 1970. 424 с.
19. Хамермеш М. Теория групп и ее применение к физическим проблемам. Изд. 3-е. М.: Либроком, 2010. 584 с.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.