Задача скачана с сайта www.MatBuro.ru

©МатБюро - Решение задач по высшей математике

Тема: Теория игр

ЗАДАНИЕ.  Найти стратегии игроков А, В и цену игры, заданной матрицей (с помощью формул и графически)

3     5     2   0

6 −1   3  5

РЕШЕНИЕ. Найдем наилучшую стратегию первого игрока: минимальное число в каждой строке обозначим ^α_i . Получаем: ^α₁ = 0, ^α₂ =−1. Выберем максимальное из этих значений α=0 - нижняя цена игры. 

Аналогично для второго игрока. Найдем максимальные значения выигрыша по столбцам:  ^β₁ = 6,^β₂ = 5,^β₃ = 3,^β₄ = 5 и минимальное из этих чисел β= 3 - верхняя цена игры. 

Так как верхняя и нижняя цены игры различны, игра не имеет решения в чистых стратегиях, цена игры находится в промежутке от 0 до 3 (между нижней и верхней ценой игры). 

Игра имеет большую размерность, попробуем ее уменьшить, выделив невыгодные стратегии и вычеркнув их из матрицы: все элементы столбца В1 больше элементов столбца В3, поэтому вычеркиваем столбец В1. 

−    5     2   0

− −1   3  5

Получили матрицу (А1, А2, В2, В3, В4):

 5     2   0

−1 3  5_  

Теперь найдем решение игры, заданной данной платежной матрицей в смешанных стратегиях.

Найдем две активные стратегии игрока B . Для этого определим оптимальные смешанные стратегии игрока A. 

Игрок B имеет три чистые стратегии,  им будут соответствовать три прямые в геометрическом решении игры. 

Вычислим средний выигрыш первого игрока, при условии, что он применяет свою смешанную стратегию, а второй – свою чистую j -ю стратегию: M j ( )x1 =(a1j −a x a2 j ) 1 + 2 j . 

Получаем:

M x_{1 1}( ) = (a₁₁ −a_{21 1})x +a₂₁ = 6x₁ −1, M₂(x₁) = (a₁₂ −a₂₂)x₁ +a₂₂ =− +x₁      3,

M₃(x₁) = (a₁₃ −a₂₃)x₁ +a₂₃ =−5x₁ +5 .

                                                                             1

Задача скачана с сайта www.MatBuro.ru

©МатБюро - Решение задач по высшей математике

Строим соответствующие прямые линии в прямоугольной системе координат: 

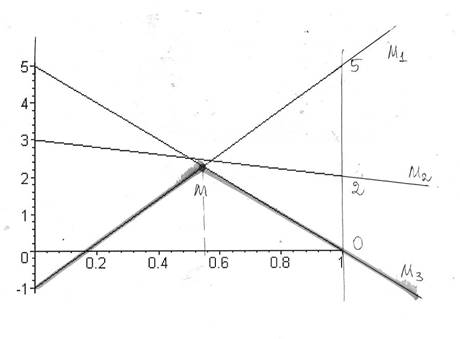
Цель второго игрока – минимизировать выигрыш первого за счет выбора своих стратегий, поэтому берем самые нижние отрезки. Цель первого игрока – максимизировать выигрыш  за счет выбора x₁, поэтому берем самую высокую точку M (см. чертеж). 

Те линии стратегии, пересечением которых образована точка M , являются активными стратегиями игрока B , в нашем случае это B₁ и B₃. Таким образом, игра сводится к игре ×2  с  матрицей ₋5₁ 0₅_.

2

Находим оптимальные стратегии:

6x₁ − =−1 5x₁ + =5 v , x₁ + x₂ =1.

Откуда x₁ = 11⁶ , x₂ = 11⁵ , v = 11²⁵ .

Теперь найдем стратегии второго игрока:

5q₁ +0q₂ = =v 11²⁵ ⇒ q₁ = 11⁵ , q₂ = 11⁶ .

Получили P^* =^_ ⁶ ; ^{5 }_ , Q^* =^_0; ⁵ ;0; ⁶ _^ . v= ²⁵ - цена игры. 

                                   11 11             11      11         11

                                                                             2