Тест по геометрии 8 класс по теме "Синус, косинус и тангенс острого угла прямоугольного треугольника"

Синус, косинус и тангенс острого угла прямоугольного треугольника

Задание 1

Вопрос:

Запишите формулу для вычисления tg α в треугольнике, изображенном на рисунке:

Изображение:

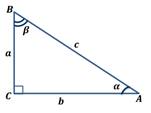
Задание 2

Вопрос:

Чему равен синус наименьшего угла прямоугольного треугольника, изображенного на рисунке? Ответ запишите в виде десятичной дроби.

Изображение:

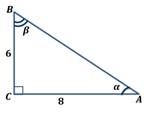
Задание 3

Вопрос:

Что можно сказать про прямоугольный треугольник, тангенс острого угла которого равен 1?

Задание 4

Вопрос:

Чему равен косинус острого угла прямоугольного треугольника, синус которого равен ? Ответ запишите в виде обыкновенной дроби.

Задание 5

Вопрос:

Вставьте пропущенное слово:

Синусом острого угла прямоугольного треугольника называется отношение ___________ катета к гипотенузе.

Задание 6

Вопрос:

Вставьте пропущенное слово:

Косинусом острого угла прямоугольного треугольника называется отношение ___________ катета к гипотенузе.

Задание 7

Вопрос:

Вставьте пропущенные слова. Укажите верное соответствие между номером и словом:

Тангенсом строго угла прямоугольного треугольника называется отношение 1)___________ катета к 2)_____________.

Задание 8

Вопрос:

Вставьте пропущенное слово:

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к _____________.

Задание 9

Вопрос:

Вставьте пропущенное слово:

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к _____________.

Контрольная работа по теме «Соотношения между сторонами и углами в прямоугольном треугольнике»