
1. ИНФОРМАЦИЯ
1.1. Количество информации
Количеством информации называют ее числовую характеристику, отражающую ту степень неопределенности, которая исчезает после получения информации. Для оценки и измерения количества информации в сообщении применяются различные подходы, среди которых следует выделить статистический и алфавитный.
Статистический подход. Для количественной оценки неопределенности или энтропии Н Хартли Р. предложил формулу, содержащую логарифм от числа равновероятных возможностей N
H = log2 N, (1)
которую можно записать в следующем виде:
2H = N, (2)
где H – количество информации.
Минимальной единицей количества информации, именуемой битом, будет выбор из двух возможностей.
При не равновероятной возможности выбора количество информации hi, зависящей от индивидуальной вероятности Pi i – го выбора, вычисляется по формуле К. Шеннона
![]() ,
(3)
,
(3)
которую можно преобразовать к виду
![]() . (4)
. (4)
Удобнее в качестве меры количества информации пользоваться не значением hi, а средним значением количества информации
![]() .
(5)
.
(5)
Алфавитный подход позволяет определить количество текстовой информации. Количество информации, которое несёт каждый символ вычисляется по формуле
i = log 2 N, (6)
где N – мощность алфавита, равная количеству символов в нём.
Текст, содержащий K символов, имеет объём информации, равный
I = K · i. (7)
Максимальное количество слов L из m букв, которое можно составить с помощью алфавита мощностью N, определяется как
П 1.1. Пусть имеется колода карт, содержащая 32 различные карты. При выборе одной карты имеется 32 возможности.
П 1.2. При бросании монеты выбор одного результата (например, выпадения орла) несет один бит информации, поскольку количество возможных равновероятных результатов N = 2 (орел или решка). Действительно, подставляя N = 2 в формулу (1), получим H = 1 бит.
П 1.3. Какой объем информации содержит сообщение, уменьшающее неопределенность в 4 раза?
Решение: так как неопределенность знаний уменьшается в 4 раза, следовательно, она была равна 4, т.е. существовало 4 равновероятных события. Сообщение о том, что произошло одно из них, несет 2 бита информации (4 = 22).
Ответ: 2 бита.
П 1.4. В коробке лежат 16 кубиков. Все кубики разного цвета. Сколько информации несет сообщение о том, что из коробки достали красный кубик?
Решение: из 16 равновероятных событий нужно выбрать одно. Поэтому N = 16, следовательно, H = 4, (16 = 24).
Пояснение: события равновероятны, т.к. всех цветов в коробке присутствует по одному.
Ответ: 4 бита.
П 1.5. Сообщение о том, что ваш друг живет на 10 этаже, несет 4 бита информации. Сколько этажей в этом доме?
Решение: N = 24 = 16 этажей.
Пояснение: события равновероятны, т.к. номера этажей не повторяются.
Ответ: 16 этажей.
Примеры решения задач с не равновероятными событиями
П 1.6. В корзине лежат 8 черных шаров и 24 белых. Сколько информации несет сообщение о том, что достали черный шар?
Дано: Nч = 8; Nб = 24. Найти: Hч = ?
Решение:
1) N = 8 + 24 = 32 – шара всего;
2) Pч = 8/32 = ¼ - вероятность доставания черного шара;
3) H = log2 (1/ ¼) = 2 бита.
Ответ: 2 бита.
П 1.7. В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей было в коробке?
Дано: Nч = 64; Hб = 4. Найти: Кб = ?
Решение:
1) Hб = log2(1/Pб); 4 = log2(1/Pб); 1/Pб = 16; Pб = 1/16 – вероятность доставания белого карандаша;
2) Pб = Кб/N; 1/16 = Кб/64; Кб = 64/16 = 4 белых карандаша.
Ответ: 4 белых карандаша.
П 1.8. В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего шаров в корзине?
Дано: Кч = 16, N = 2 бита. Найти: N - ?
Решение:
1) 1/Pб = 21, 1/Pб = 22 = 4, Pб = ¼ - вероятность доставания белого шара;
2) Pб = Кб/N = Кб/(Кб + Кч), ¼ = Кб/(Кб + 18), Кб + 18 = 4 * Кб, 18 = 3 * Кб, Кб = 6 – белых шаров;
3) N = Кб + Кч = 18 + 6 = 24 шара было в корзине.
Ответ: 24 шара лежало в корзине.
Примеры решения задач на измерение алфавитного объёма
П 1.9. Найти объем текста HT, записанного на языке, алфавит которого содержит N = 128 символов и K = 2000 символов в сообщении.
Решение:
1) H = log2N = log2128 = 7 бит – объем одного символа.
2) HT = H × K = 7 × 2000 = 14 000 бит – объем сообщения.
Ответ: 14 000 бит.
П 1.10. В алфавите некоторого языка всего N = 2 буквы, каждое слово в языке состоит точно из m = 7 букв. Какой максимальный запас слов в языке?
а) 128; б) 256; в) 64; г) 1024.
Решение:
Если мощность алфавита N, а максимальное количество букв в слове, записанном с помощью этого алфавита, – m, то максимально возможное количество слов определяется по формуле L = Nm, откуда N = 27, следовательно, N = 128.
Т 1.1. «Вы выходите на следующей остановке?» - спросили человека в автобусе. «Нет», - ответил он. Сколько информации содержит ответ?
Варианты ответа: а) 1 бит; б) 2 бита; в) 3 бита; г) 4 бита.
Т 1.2. Сколько информации содержит сообщение, уменьшающее неопределенность знаний в 8 раз?
Варианты ответа: а) 1 бит; б) 2 бита; в) 3 бита; г) 4 бита.
Т 1.3. При угадывании целого числа в некотором диапазоне было получено 8 бит информации. Сколько чисел содержит этот диапазон?
Варианты ответа: а) 128; б) 256; в) 64; г) 32.
Т 1.4. В школьной библиотеке 16 стеллажей с книгами. На каждом стеллаже 8 полок. Библиотекарь сообщил Пете, что нужная ему книга находится на пятом стеллаже на третьей сверху полке. Какое количество информации библиотекарь передал Пете?
Варианты ответа: а) 5 бит; б) 6 бит; в) 7 бит; г) 8 бит.
Т 1.5. При угадывании целого числа в диапазоне от 1 до N было получено 9 бит информации. Чему равно N?
Варианты ответа: а) 64; б) 128; в) 256; г) 512.
Т 1.6. В группе N = 30 студентов. За контрольную работу по математике получено К5 = 15 пятерок, К4 = 6 четверок, К3 = 8 троек и К2 = 1 двойка. Какое количество информации Н5 в сообщении о том, что Андреев получил пятерку?
Варианты ответа: а) 1 бит; б) 2 бита; в) 3 бита; г) 4 бита.
Т 1.7. За семестр студент получил N = 100 оценок. Сообщение о том, что он получил пятерку, несет Н5 =2 бита информации. Сколько пятерок К5 студент получил за четверть?
Варианты ответа: а) 15; б) 20; в) 25; г) 30.
Т 1.8. В ящике лежат перчатки (белые и черные). Среди них – Кч = 2 пары черных. Сообщение о том, что из ящика достали пару черных перчаток, несет Нч = 4 бита информации. Сколько пар белых перчаток Кб было в ящике?
Варианты ответа: а) 20; б) 30; в) 40; г) 48.
Т 1.9. Для ремонта актового зала использовали белую, синюю и коричневую краски. Израсходовали одинаковое количество банок белой и синей краски Кб = Кс. Сообщение о том, что закончилась банка белой краски, несет Нб = 2 бита информации. Синей краски израсходовали Кс = 8 банок. Сколько банок коричневой краски Кк израсходовали на ремонт актового?
Варианты ответа: а) 8; б) 12; в) 16; г) 20.
Т 1.10. На остановке останавливаются троллейбусы с разными номерами. Сообщение о том, что к остановке подошел троллейбус с номером N1, несет НN1 = 4 бита информации. Вероятность появления на остановке троллейбуса с номером N2 в два раза меньше, чем вероятность появления троллейбуса с номером N1 (РN1 = 2РN2). Сколько информации НN2 несет сообщение о появлении на остановке троллейбуса с номером N2?
Варианты ответа: а) 5 бит; б) 6 бит; в) 7 бит; г) 8 бит.
Т 1.11. В корзине лежат 32 клубка шерсти. Среди них – 4 красных. Сколько информации несет сообщение о том, что достали клубок красной шерсти?
Варианты ответа: а) 1 бит; б) 2 бита; в) 3 бита; г) 4 бита.
Т 1.12. В корзине лежат красные и зеленые шары. Среди них 15 красных шаров. Сообщение о том, что из корзины достали зеленый шар, несет 2 бита информации. Сколько всего в корзине шаров?
Варианты ответа: а) 18; б) 20; в) 22; г) 24.
Т 1.13. Известно, что в ящике лежат N = 20 шаров. Из них – Кс = 10 синих, Кз = 5 – зеленых, Кж = 4 – желтых и Кк = 1 – красный. Какое количество информации несут сообщения о том, что из ящика случайным образом достали черный шар Нч, белый шар Нб, желтый шар Нж, красный шар Нк?
Варианты ответа:
а) Нч = 1 бит, Нб = 2 бита, Нж = 2,236 бит, Нк = 4,47 бит.
б) Нч = 2 бита, Нб = 4 бита, Нж = 2, 6 бит, Нк = 4,47 бит.
в) Нч = 1 бит, Нб = 2 бита, Нж = 3 бита, Нк = 4 бита.
г) Нч = 3 бита, Нб = 2 бита, Нж = 2,236 бит, Нк = 4,47 бит.
Т 1.14. В корзине находятся всего 128 красных, синих и белых шаров, причем красных шаров в три раза больше, чем синих. Сообщение о том, что достали белый шар, содержит 3 бита информации. Найти количество синих шаров. Варианты ответа: а) 24; б) 28; в) 32; г) 36.
Т 1.15. В озере обитает 12500 окуней, 25000 пескарей, а карасей и щук по 6250. Сколько информации мы получим, когда поймаем какую-нибудь рыбу?
Варианты ответа: а) 1, 5 бит; б) 1, 75 бит; в) 2 бита; г) 2, 25 бит.
Т 1.16. Сообщение, записанное буквами из 64-х символьного алфавита, содержит 20 символов. Какой объем информации оно несет?
Варианты ответа: а) 100 бит; б) 110 бит; в) 120 бит; г) 130 бит.
Т 1.17. Информационное сообщение объемом 1,5 Кбайта содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?
Варианты ответа: а) 8; б) 16; в) 24; г) 32.
Т 1.18. Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Какой объем информации содержат 5 страниц текста?
Варианты ответа: а) 850 байт; б) 950 байт; в) 1050 байт; г) 1150 байт.
Т 1.19. В алфавите некоторого языка всего две буквы: «А» и «Б». Все слова, записанные на этом языке, состоят из 11 букв. Какой максимальный словарный запас может быть у этого языка?
Варианты ответа: а) 22; б) 11; в) 2048; г) 1024; д) 44.
Т 1.20. Словарный запас некоторого языка составляет 256 слов, каждое из которых состоит точно из 4 букв. Сколько букв в алфавите языка?
Варианты ответа: а) 8; б) 4; в) 64; г) 1024; д) 256.
1.2. Представление числовой информации
Системы исчисления
Система счисления – это способ представления чисел и соответствующие ему правила действия с числами.
Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает.
Примером непозиционной системы счисления является римская система (римские цифры). В римской системе в качестве цифр используются латинские буквы:
I V X L C D M
1 5 10 50 100 500 1000
П 1.11. Число CCXXXII складывается из двух сотен, трех десятков и двух единиц и равно 232.
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются, например:
VI = 5 + 1 = 6, а IV = 5 – 1 = 4.
П 1.12. Записать римское число MCMXCVIII в десятичной системе
MCMXCVIII = 1000 + (- 100 + 1000) + (-10 +100) + 5 + 1 + 1+ 1 = 1998.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием позиционной системы счисления.
Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Позиционный характер этой системы легко понять на примере любого многозначного числа. Например, в числе 333 первая тройка означает три сотни, вторая – три десятка, третья – три единицы.
Для записи чисел в позиционной системе с основанием n нужно иметь алфавит из n цифр. Обычно для этого при n < 10 используют n первых арабских цифр, а при n > 10 к десяти арабским цифрам добавляют буквы. Вот примеры алфавитов нескольких систем:
|
Основание |
Название |
Алфавит |
|
n = 2 |
двоичная |
0 1 |
|
n = 3 |
троичная |
0 1 2 |
|
n = 8 |
восьмеричная |
0 1 2 3 4 5 6 7 |
|
n = 16 |
шестнадцатеричная |
0 1 2 3 4 5 6 7 8 9 A B C D E F |
Если требуется указать основание системы, к которой относится число, то оно приписывается нижним индексом к этому числу. Например: 1011012, 36718, 3В8F16.
В системе счисления с основанием q (q-ичная система счисления) единицами разрядов служат последовательные степени числа q. q единиц какого-либо разряда образуют единицу следующего разряда. Для записи числа в q-ичной системе счисления требуется q различных знаков (цифр), изображающих числа 0, 1, …, q – 1. Запись числа q в q-ичной системе счисления имеет вид 10. Развернутой формой записи числа называется запись в виде
![]()
Здесь Aq –само число, q – основание системы счисления, ai – цифры данной системы счисления, n – число разрядов целой части числа, m – число разрядов
дробной части числа.
Свернутой формой записи числа называется запись в виде
![]()
которой пользуются в повседневной жизни.
П 1.13. Записать в развернутом виде число А10 = 4718,63
А10 = 4*103 + 7*102 + 1*101 + 8*100 + 6*10-1 + 3*10-2 .
П 1.14. Записать в развернутом виде число А8 = 7764,1
А8 = 7*83 + 7*82 + 6*81 + 4*80 + 1*8-1 .
П 1.15. Записать в развернутом виде число А16 = 3АF
А16 = 3*163 + 10*161 + 15*160 .
П 1.16. Все числа 1123, 1011012, 15FC16, 101,112 перевести в десятичную систему
1123 = 1*32 + 1*31 + 2*30 = 9 + 3 + 2 = 1410,
1011012 = 1*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 32 + 8 + 4 + 1 = 4510,
15FC16 = 1*163 + 5*162 + 15*161 + 12 = 4096 + 1280 + 240 + 12 = 562810,
101,112 = 1*22 + 0*21 + 1*20 + 1*2-1 + 1*2-2 = 4 + 1 + ½ + ¼ = 5 + 0,5 + 0, 25 = 5,7510.
П 1.17. У жителей села «Не десятичное» на ферме имеется 120 голов рогатого скота, из них 53 коровы и 34 быка. Какая система счисления используется сельчанами?
Решение: Самая большая цифра в рассматриваемых числах – это цифра 5. Значит, она входит в состав алфавита искомой системы счисления. Тогда основание системы счисления больше 5. Задачу можно решить методом подстановки оснований 6 и 7 или математически.
Примем за х основание искомой системы счисления. Тогда после перевода чисел, стоящих в правой и левой частях, в десятичную систему счисления получим следующее равенство: х2 + 2х = 5х + 3 + 3х + 4. После преобразований получим уравнение х2 – 6х – 7 = 0.
Ответ х = 7.
Перевод десятичных чисел в другие системы счисления
1) Последовательно выполнить деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получите неполное частное, меньшее делителя;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего частного.
П 1.18. Перевести число 3710 в двоичную систему счисления. Для обозначения цифр в записи числа используем символику: а5 а4 а3 а2 а1 а0.
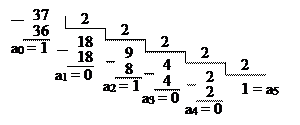 Отсюда 3710 = 1001012.
Отсюда 3710 = 1001012.
П 1.19. Перевести десятичное число 315 в восьмеричную и в шестнадцатеричную системы счисления:
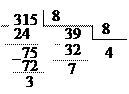 |
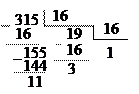 |
Отсюда следует: 31510 = 4738 = 13В16.
Напомним, что 1110 = В16.
Перевод двоичных чисел в системы счисления с основанием 2n
Для того, чтобы целое двоичное число записать в системе счисления с основанием q = 2n (4, 8, 16 и т.д.), нужно:
1) данное двоичное число разбить справа налево на группы по n цифр в каждой группе;
2) если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q = 2n.
Ниже приводится таблица с числами систем счисления с основаниями q = 2n, где n = 1, 3, 4 и десятичной системы счисления.
|
Десятичная |
Двоичная |
Восьмеричная |
Шестнадцатеричная |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
2 |
10 |
2 |
2 |
|
3 |
11 |
3 |
3 |
|
4 |
100 |
4 |
4 |
|
5 |
101 |
5 |
5 |
|
6 |
110 |
6 |
6 |
|
7 |
111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
1001 |
11 |
9 |
|
10 |
1010 |
12 |
А |
|
11 |
1011 |
13 |
B |
|
12 |
1100 |
14 |
C |
|
13 |
1101 |
15 |
D |
|
14 |
1110 |
16 |
E |
|
15 |
1111 |
17 |
F |
П 1.20. Перевести число 11001010011010101112 в восьмеричную систему счисления.
Разбиваем число на группы по три цифры – триады (т.к. q = 8, 8 = 2n, n = 3) справа налево и, пользуясь таблицей, записываем соответствующее восьмеричное число.
|
001 |
100 |
101 |
001 |
101 |
010 |
111 |
|
1 |
4 |
5 |
1 |
5 |
2 |
7 |
Ответ: 14515278
П 1.21. Перевести число 11001010011010101112 в шестнадцатеричную систему счисления.
Разбиваем число на группы по четыре цифры – тетрады (т.к. q = 16, 16 = 2n, n = 4) справа налево и, пользуясь таблицей, записываем соответствующее шестнадцатеричное число.
|
0110 |
0101 |
0011 |
0101 |
0111 |
|
6 |
5 |
3 |
5 |
7 |
Ответ: 6535716
П 1.22. Чему равно значение основания системы счисления Х, если известно, что 175Х = 7D16?
Решение: Запишем числа 175Х и 7D16 в десятичной системе счисления.
175Х = Х 2 + 7Х + 5,
7D16 = 7·16 + 13 = 125.
Но так как эти числа равны, то Х 2 + 7Х + 5 = 125.
Корни полученного квадратного уравнения: Х = 8 и Х = -15 (не подходит, так как основание системы счисления не может быть отрицательной величиной). Следовательно, основание системы счисления – 8.
Для того, чтобы произвольное число, записанное в системе счисления с основанием q = 2n, перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-разрядным эквивалентом в двоичной системе счисления.
Применительно к компьютерной информации часто используются системы с основанием 8 (восьмеричная) или 16 (шестнадцатеричная).
П 1.23. Перевести двоичное число 110111101011101111 в шестнадцатеричную систему счисления.
Решение: Разделим данное число на группы по четыре цифры, начиная справа. Если в крайней левой группе окажется меньше четырех цифр, то дополним ее нулями
0011 0111 1010 1110 1111.
А теперь, глядя на двоично-шестнадцатеричную таблицу, заменим каждую двоичную группу на соответствующую шестнадцатеричную цифру
3 7 А Е F.
Следовательно
1101111010111011112 = 37AEF16.
Тестовые задачи
Т 1.21. В саду 100q плодовых кустарников, из них 33 куста малины, 22 куста смородины красной, 16 кустов черной смородины и 17 кустов крыжовника. В какой системе счисления подсчитаны деревья?
Варианты ответа: а) 7; б) 9; в) 11; г) 13.
Т 1.22. Было 53q груши. После того, как каждую из них разрезали пополам, стало 136 половинок. В системе счисления с каким основанием вели счет?
Варианты ответа: а) 11; б) 13; в) 15; г) 17.
Т 1.23. Какое число больше?
Варианты ответа: а) 1527; б) 15210; в) 15212; г) 15216.
Т 1.24. Переведите двоичные числа в восьмеричную систему счисления:
а) 110000110101; 1010101 б) 11100001011001; 1000010101.
Т 1.25. Переведите двоичные числа в шестнадцатеричную систему счисления: а) 11011010001; 111111111000001 б) 10001111010; 100011111011.
Т 1.26. Переведите шестнадцатеричные числа в двоичную систему счисления: а) 1АС7 б) FACC.
Т 1.27. Переведите числа из восьмеричной системы счисления в шестнадцатеричную: а) 774; б) 665.
1.3. Представление символьной информации
Правило представления символьной информации (буквы алфавита и другие символы) заключается в том, что каждому символу в компьютере ставиться в соответствие двоичный код – совокупность нулей и единиц.
Так, 1 бит (принимающий значения 0, 1) позволяет кодировать 2 символа, 2 бита (00, 01, 10, 11) – 4 символа, 3 бита (000, 001, 010, 100, 011, 101, 110, 111) – 8 символов и, наконец, n бит – 2n символов. Минимальное количество бит n, необходимое для кодирования N символов определяется по формуле
N ≤ 2n. (9)
С текстовыми данными можно производить следующие операции: сравнение двоичных кодов (>, <, =, ≠), слияние и разбиение текста на отдельные символы или группы символов.
В наиболее распространенном ASCII стандарте кодировки каждому символу поставлено в соответствие двоичное число от 0 до 255 (8-битовый двоичный код), например: А – 01000001 (41), В – 01000010 (42), С – 01000011 (43), D – 01000100 (44) и т.д. Символы от 0 до 127 – латинские буквы, цифры и знаки препинания – составляют постоянную (базовую) часть таблицы. Расширенная таблица от 128 до 255 символов отводиться под национальный стандарт.
В настоящее время идет внедрение нового стандарта – Unicode. Этот стандарт определяет кодировку каждого символа двумя байтами. Соответственно, число одновременно все известные символы, в том числе японские и китайские иероглифы.
Существуют и национальные стандарты кодировки. Например, в СССР был введен стандарт КОИ-8 (код обмена информацией восьмизначный), который по сей день используется для кодировки текста.
П 1.24. Какое количество бит необходимо для кодирования 33 строчных и прописных букв русского алфавита.
Решение. Всего необходимо закодировать N = 66 букв, для чего согласно формуле (9)
![]()
потребуется n = 7 бит.
П 1.25. Закодируйте в двоичном, десятичном и шестнадцатеричном коде слово АВВА.
Ответ:
1) в двоичном коде: АВВА2 = 01000001 01000010 0100001001000001.
2) в десятичном коде:
А10 = 0*27 + 1*26 + 0*25 + 0*24 + 0*23 + 0*22 + 0*21 + 1*20 = 65
В10 = 0*27 + 1*26 + 0*25 + 0*24 + 0*23 + 0*22 + 1*21 + 0*20 = 66
АВВА10 = 65666665
3) в шестнадцатеричном коде
А16 = 41, В16 = 42.
АВВА16 = 41424241.
П 1.26. Какое максимальное количество символов может содержать кодировочная таблица, если при хранении один символ из этой таблицы занимает 10 бит памяти?
а) 800; б) 80; в) 1024; г) 512; д) 256.
Ответ: в.
Пояснение: необходимо воспользоваться формулой 2i = N, где i = 10 бит. Тогда N = 210 = 1024 – количество символов в кодировочной таблице.
П 1.27. Выбрать слово, имеющее наибольшую сумму кодов символов в таблице кодировки ASCII.
а) окно; б) кино; в) ника; г) конь; д) ночь.
Ответ: д.
Пояснение: При решении этой задачи используется принцип последовательного кодирования. Буквы в кодировочной таблице располагаются в алфавитном порядке. Нет необходимости знать код каждой буквы. Сопоставим, например, слова «кино» и «ника». Они отличаются только одной буквой. Код (номер) буквы «о» больше, чем код буквы «а». Следовательно, слово «кино» имеет большую сумму кодов символов. Аналогично проведем анализ остальных слов.
Тестовые задачи
Т 1.28. Выбрать фрагмент текста, имеющий минимальную сумму кодов в таблице ASCII.
Варианты ответа: а) 2b2d; б) файл; в) file; г) 1999; д) 2001.
Т 1.29. Какое минимальное количество бит потребуется для кодирования 26 прописных и строчных латинских букв.
Варианты ответа: а) 5 бит; б) 6 бит; в) 7 бит; г) 8 бит.
Т 1.30. В каком порядке будут идти фрагменты текста «excel», «байт», «8в», «10г», «9а», «10а», если упорядочить их по убыванию?
Варианты ответа:
а) байт, excel, 8в, 9а, 10г, 10а;
б) байт, excel, 8в, 9а, 10а, 10г;
в) 10а, 10г, 9а, 8в, байт, excel;
г) байт, excel, 10г, 10а, 9а, 8в;
д) excel, байт, 10г, 10а, 9а, 8в.
Т 1.31. Во сколько раз увеличиться информационный объем страницы текста при его преобразовании из кодировки Windows 1251 (таблица кодировки содержит 256 символов) в кодировку Unicode (таблица кодировки содержит 65536 символов)?
Варианты ответа: а) 2; б) 4; в) 6; г) 8.
1.4. Представление графической информации
Графическая информация представляет собой изображение, сформированное из определенного числа точек, именуемых пикселями. Качество изображения зависит от количества цветов и точек, составляющих изображение.
Пиксель – наименьший элемент изображения на экране (точка на экране).
Растр – прямоугольная сетка пикселей на экране.
Разрешающая способность экрана – размер сетки растра, задаваемого в виде произведения M×N, где M – число точек по горизонтали, N – число точек по вертикали (число строк).
Видеоинформация – информация об изображении, воспроизводимом на экране компьютера, хранящаяся в компьютерной памяти.
Видеопамять – оперативная память, хранящая видеоинформацию во время ее воспроизведения в изображение на экране.
Графический файл – это файл, хранящий информацию о графическом изображении.
Разрешающей способностью называют количество точек, которую определяют 4 основных ее значения: 640×480, 800×600, 1024×768, 1280×1024.
Битовой глубиной цвета называется количество бит, необходимое для кодирования цвета точки. Наиболее распространенными значениями битовой глубины цвета являются 4, 8, 16 и 24 бита на точку.
Количество цветов можно вычислить по формуле N = 2i, где i – битовая глубина цвета.
При кодировании цвета в основном используют две цветовые модели: RBG (R, Red – красный; B, Blue – синий; G, Green – зеленый) и CMYK (C, Cyan – голубой; M, Magenta – пурпурный; Y, Yellow – желтый; K, Black – черный).
П 1.28. Какой объем видеопамяти необходим для хранения четырех страниц изображения при условии, что разрешающая способность дисплея равна 640×480 точек, а используемых цветов – 32?
Решение:
1) N = 2i, 32 = 2i, i = 5 бит – глубина цвета;
2) 640*480*5*4 = 6144000 = 750 Кбайт.
Ответ: 750 Кбайт.
П 1.29. Объем видеопамяти равен 1875 Кбайтам и она разделена на 2 страницы. Какое максимальное количество цветов можно использовать при условии, что разрешающая способность экрана монитора 800×600?
Решение:
1) 1875*1024*8 = 30720000 бит – объем видеопамяти;
2) 30720000:800:600:2 = 16 бит – глубина цвета;
3) N = 2i = 216 = 65536 цветов.
Ответ: 65536 цветов.
П 1.30. 265-цветный рисунок содержит 1Кайт информации. Из скольких точек он состоит?
Решение:
1) N = 2i, 256 = 2i, i = 8 бит – информационный объем одной точки;
2) 1024*8 = 8192 бит – объем изображения;
3) 8192:8 = 1024 точек – на изображении.
Ответ: 1024 точек.
П 1.31. После преобразования графического изображения количество цветов уменьшилось с 256 до 32. Во сколько раз уменьшился объем занимаемой памяти?
Решение:
1) N1 = 2i, 256 = 2i, i1 = 8;
2) N2 = 2i, 32 = 2i, i2 = 5;
3) i1 / i2 = 8/5 = 1,6 раза.
Ответ: 1,6 раз.
Тестовые задачи
Т 1.32. Какой объем видеопамяти необходим для хранения двух страниц изображения при условии, что разрешающая способность дисплея равна 640×350 пикселей, а количество используемых цветов – 16?
Варианты ответа: а) 54,3 Кбайт; б) 124,3 Кбайт; в) 174,4 Кбайт ; г) 218,7 Кбайт.
Т 1.33. Какой объем видеопамяти необходим для хранения четырех страниц изображения, если битовая глубина равна 24, а разрешающая способность дисплея – 800×600 пикселей?
Варианты ответа: а) 4,8 Мбайт; б) 5,5 Мбайт; в) 6,7 Мбайт; г) 7,2 Мбайт.
Т 1.34. Объем видеопамяти равен 1 Мбайт. Разрешающая способность дисплея – 800×600. Какое максимальное количество цветов можно использовать при условии, что видеопамять делится на две страницы?
Варианты ответа: а) 64; б) 128; в) 256; г) 512.
Т 1.35. Битовая глубина равна 32, видеопамять делится на две страницы, разрешающая способность дисплея – 800×600. Вычислить объем видеопамяти.
Варианты ответа: а) 3,7 Мбайт; б) 4,8 Мбайт; в) 5,5 Мбайт; г) 6,4 Мбайт.
Т 1.36. Видеопамять имеет объем, в котором может храниться 4-х цветное изображение размером 640×480. Какого размера изображение можно хранить в том же объеме видеопамяти, если использовать 256-цветную палитру?
Варианты ответа: а) 160×120; б) 320×240; в) 640×480; г) 800×600.
Т 1.37. На экране монитора необходимо получить 1024 оттенка серого цвета. Какой должна быть глубина цвета?
Варианты ответа: а) 10 бит; б) 20 бит; в) 30 бит; г) 40 бит.
Т 1.38. Объем видеопамяти – 2 Мбайта, разрешающая способность дисплея равна 800×600. Сколько оттенков серого цвета можно получить на экране при условии, что видеопамять делится на две страницы?
Варианты ответа: а) 512; б) 1024; в) 1536; г) 2048.
Ответ: 1024 оттенка.
Т 1.39. Объем видеопамяти равен 2,5 Мбайта, глубина цвета – 16, разрешающая способность экрана монитора – 640×480 точек. Найти максимальное количество страниц, которое можно использовать при этих условиях. Варианты ответа: а) 2; б) 3; в) 4; г) 5.
Т 1.40. Видеопамять имеет объем, в котором может хранится 8-цветное изображение размером 640×350 точек. Какого размера изображение можно хранить в том же объеме видеопамяти, если использовать 512-цветную палитру? Варианты ответа: а) 151245; б) 182434; в) 253624; г) 273066.
Т 1.41. После преобразования графического изображения количество цветов увеличилось с 256 до 65536. Во сколько раз увеличился объем занимаемой памяти?
Варианты ответа: а) 3,5; б) 2,5; в) 1,5; г) 0,5.
Т 1.42. Растровый графический редактор предназначен для:
а) создания чертежей; в) построения диаграмм;
б) построения графиков; г) создания и редактирования рисунков.
Т 1.43. Из предложенного списка графическими форматами является:
1) TIFF; 2) TXT; 3) MPI; 4) JPG; 5) BMP.
Верные утверждения содержатся в варианте ответа:
а) 2, 3, 5; б) 1, 4, 5; в) 4, 5; г) 1, 2.
Т 1.44. Энтропия в информатике – это свойство:
а) данных; б) знаний; в) информации; г) условий поиска.
Т 1.45. Семантический аспект информации:
а) определяет информацию с точки зрения ее практической полезности для получателя;
б) определяет отношения между единицами информации;
в) определяет значение символа естественного алфавита;
г) дает возможность раскрыть ее содержание и показать отношение между смысловыми значениями ее элементов.
Т 1.46. СMYK является:
а) графическим редактором; б) системой представления цвета;
в) форматом графических файлов; г) типом монитора.
Т 1.47. Если 1110 = 23х, то основание системы счисления Х равно:
а) 4; б) 8; в) 10; г) 16.82.
Т 1.48. Словарный запас некоторого языка составляет 256 слов, каждое из которых состоит точно из 4 букв. Сколько букв в алфавите языка?
а) 8; б) 4; в) 64; г) 1024; д) 256.
2. ТЕХНИЧЕСКИЕ СРЕДСТВА РЕАЛИЗАЦИИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ
2.1. Основные этапы развития информатики и вычислительной техники
С этой темой можно ознакомиться в разделе 2.1. пособия [1].
Тестовые задачи
Т 2.1. Установите хронологическую последовательность изобретения перечисленных приспособлений для счета:
а) аналитическая машина Ч. Беббиджа; б) арифмометр «Паскалина»;
в) абак; г) счеты.
Т 2.2. Первым программистом считается:
а) Готфрид Лейбниц; б) Ада Лавлейс;
в) Джон фон Нейман; г) Блез Паскаль.
Т 2.3. Продолжите фразу: «Деление электронной вычислительной техники на поколения обусловлено…»
а) исторической обстановкой; б) развитием элементной базы;
в) уменьшением размеров компьютеров; г) развитием науки.
Т 2.4. Установите соответствие между поколениями ЭВМ и основными составляющими элементной базы. К каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
|
|
Поколение ЭВМ |
|
Элементная база |
|
1 |
I поколение |
а |
Микросхемы |
|
2 |
II поколение |
б |
БИС, СБИС |
|
3 |
III поколение |
в |
Транзисторы |
|
4 |
IV поколение |
г |
Электронные лампы |
Запишите в таблицу выбранные буквы, а затем получившуюся последовательность букв без пробелов и других символов запишите в ответ.
2.2. Состав и назначение основных элементов персонального компьютера
С этой темой можно ознакомиться в разделе 2.2. пособия [1].
Тестовые задачи
Т 2.5. В левой части таблицы приведены названия носителей, а в правой – их возможная емкость. К каждой позиции левого столбца подберите соответствующую позицию из правого столбца.
|
|
Носитель |
|
Емкость |
|
1 |
Жесткий диск |
а |
256Мбайт – 2Гбайт |
|
2 |
Флоппи-диск |
б |
700Мбайт |
|
3 |
CD-RW |
в |
1,44Мбайт |
|
4 |
Флэш-память |
г |
80Мбайт и более |
Запишите в таблицу выбранные буквы, а затем получившуюся последовательность букв без пробелов и других символов запишите в ответ.
Т 2.6. Что из перечисленного является носителем информации?
1. дистрибутив; 2. флоппи-диск; 3. блокнот; 4. пластинка; 5. дисковод.
Выберите правильный вариант ответа:
а) 2, 3, 4, 5; б) 2, 3, 4; в) 1, 2, 5; г) 1, 2, 4, 5.
Т 2.7. Что из перечисленного входит в состав системы НЖМД?
1. головки записи / чтения; 2. гибкий диск; 3. дисковод; 4. жесткий диск.
Выберите правильный вариант ответа:
а) 1, 2, 3; б) 1, 2, 4; в) 1, 2, 3; г) 1, 2, 4.
Т 2.8. К какому типу памяти относится жесткий диск персонального компьютера?
а) внутренняя; б) внешняя; в) центральная; г) переносная.
Т 2.9. Теоретические основы функционирования и структуры ЭВМ разработаны группой ученых под руководством:
а) Джона фон Неймана; б) Билла Гейтса;
в) Эмиля Поста; г) Алана Тьюринга.
Т 2.10. Во время исполнения прикладная программа хранится:
а) в видеопамяти; б) в процессоре;
в) в оперативной памяти; г) в ПЗУ.
Т 2.11. При отключении компьютера информация стирается:
а) из оперативной памяти; б) из постоянного запоминающего устройства;
в) на магнитном диске; г) на компакт-диске.
2.3. Устройства ввода (вывода)
С этой темой можно ознакомиться в разделе 2.3. пособия [1].
Тестовые задачи
Т 2.12. Установите соответствие между периферийными устройствами компьютера и их разновидностью в классификации. К каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
|
|
Носитель |
|
Емкость |
|
1 |
Сканер |
а |
Устройство ввода |
|
2 |
Плоттер |
б |
Устройство вывода |
|
3 |
Световое перо |
в |
|
|
4 |
Джойстик |
г |
|
|
5 |
Колонки |
д |
|
|
6 |
Микрофон |
е |
|
Запишите в таблицу выбранные буквы, а затем получившуюся последовательность букв без пробелов и других символов запишите в ответ.
Т 2.13. Какое из перечисленных устройств вывода можно использовать для ввода информации?
а) монитор с сенсорным экраном; б) принтер – копир;
в) плоттер; г) звуковые колонки.
3. ПРОГРАММНЫЕ СРЕДСТВА РЕАЛИЗАЦИИ
С этой темой можно ознакомиться в главе 3 пособия [1].
Тестовые задачи
Т 3.1. Выберите операционную
систему:
а) Adobe; б) IBM PC; в) API; г) UNIX.
Т 3.2. Редактирование текста представляет собой:
а) процесс внесения изменений в имеющийся текст;
б) процедуру сохранения текста на диске в виде текстового файла;
в) процесс передачи текстовой информации по компьютерной сети;
г) процедуру считывания с внешнего запоминающего устройства ранее
созданного текста.
Т 3.3. Задан полный путь к файлу C:\KOD\MOD\text.doc. Каково содержимое корневого каталога диска С:
а) MOD; б) KOD; в) KOD\MOD; г) text.doc.
Т 3.4. В основные функции операционной системы не входит:
а) организация файловой структуры; б) обеспечение диалога с пользователем;
в) разработка программ для ЭВМ; г) управление ресурсами компьютера.
Т 3.5. Для управления файлами и папками в ОС Windows можно использовать:
а) панель управления; б) проводник; в) меню кнопки «Пуск»; г) панель задач.
Т 3.6. В текстовом редакторе при задании параметров страницы устанавливаются:
а) гарнитура, размер, начертание; б) отступ, интервал;
в) поля, ориентация; г) стиль, шаблон.
Т 3.7. Установите соответствие между приложениями, перечисленными в первом столбце, и их назначением во втором столбце таблицы.
|
|
Приложение |
|
Назначение приложения |
|
1 |
WinRar |
а |
Файловый менеджер |
|
2 |
Doctor Web |
б |
Восстановление поврежденных файлов и дисков |
|
3 |
Windows Commander |
в |
Архивация и разархивация данных |
|
4 |
ScanDick |
г |
Антивирусная проверка |
Выберите правильный ответ.
а) г в а б; б) в г б а; в) в г а б; г) б г а в.
Т 3.8. Из предложенного списка файлов:
1) .doc; 2) .gif; 3).jpg; 4) .exe; 5) .bmp; 6) .bak,
выберите расширения графических файлов:
а) 1,3,5; б) 2,3,4; в) 2,3,5; г) 3,5,6.
4. МОДЕЛИ РЕШЕНИЯ ФУНКЦИОНАЛЬНЫХ И ВЫЧИСЛИТЕЛЬНЫХ ЗАДАЧ
4.1. Основы логики
Логические выражения и операции
Логика – это наука о формах и способах мышления. Это учение о способах рассуждений и доказательств.
Законы мира, сущность предметов, общее в них мы познаем посредством абстрактного мышления. Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны.
Мышление всегда осуществляется через понятия, высказывания и умозаключения.
Понятие – это форма мышления, которая выделяет существенные признаки предмета или класса предметов, позволяющие отличать их от других.
Высказывание – это формулировка своего понимания окружающего мира. Высказывание является повествовательным предложением, в котором что-либо утверждается или отрицается.
По поводу высказывания можно сказать, истинно оно или ложно.
П 4.1. Истинное высказывание: «Буква «а» - гласная».
Ложное высказывание: «Компьютер был изобретен в середине XIX века».
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение (знание или вывод).
Алгебра логики отвлекается от смысловой содержательности высказываний и принимает во внимание только истинность или ложность высказывания.
Можно определить понятия логической переменной, логической функции и логической операции.
Логическая переменная – это простое высказывание, содержащее только одну мысль. ЕЕ символическое обозначение – латинская буква (например, A, B, X, Y и т.д.). Значением логической переменной могут быть только константы ИСТИНА или ЛОЖЬ; True (T) или False (F); 1 или 0.
Составное высказывание – это логическая функция, которая содержит несколько простых мыслей, соединенных между собой с помощью логических операций. Ее символическое обозначение – F(A, B,…).
На основании простых высказываний могут быть построены составные высказывания.
Логические операции – это логическое действие.
Рассмотрим три базовые логические операции – отрицание, конъюнкцию, дизъюнкцию и дополнительные – импликацию и эквивалентность.
A |
B |
|
|
|
|
А↔В |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
Если составное высказывание (логическую функцию) выразить в виде формулы, в которую войдут логические переменные и знаки логических операций, то получится логическое выражение, значение которого можно вычислить. Значением логического выражения могут быть только ЛОЖЬ или ИСТИНА. При составлении логического выражения необходимо учитывать порядок выполнения логических операций, а именно:
1) действия в скобках;
2) инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.
П 4.2. Записать в виде логического выражения следующее высказывание: «Летом Петя поедет в деревню и, если будет хорошая погода, то он пойдет на рыбалку».
1. Проанализируем составное высказывание.
Оно состоит из следующих простых высказываний: «Петя поедет в деревню», «Будет хорошая погода», «Он пойдет на рыбалку». Обозначим их через логические переменные:
А = Петя поедет в деревню;
В = Будет хорошая погода;
С = Он пойдет на рыбалку.
2. Запишем высказывание в виде логического выражения, учитывая порядок действий. Если необходимо, расставим скобки:
F = A Λ (B→C).
П 4.3. Есть два простых высказывания:
А – «Число 10 – четное»
В – «Волк – травоядное животное».
Составьте из них все возможные высказывания и определите их истинность. Ответ:
AΛB |
A V B |
|
|
A → B |
A ↔ B |
|
Ложь (0) |
Истина (1) |
Ложь (0) |
Истина (1) |
Ложь (0) |
Ложь (0) |
Составить и записать сложные высказывания из простых с использованием логических операций.
Т 4.1. Неверно, что ![]() и
Z < 0.
и
Z < 0.
Варианты ответа:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]()
Т 4.2. Z является min (Z, Х, Y).
Варианты ответа:
а) (Z < Y)Λ(Z < X); б) (Z > Y)Λ(Z < X);
в) (Z < Y)V(Z < X); г) (Z < Y)Λ(Z > X).
Т 4.3. А является max (A, B, C).
Варианты ответа:
а) (A > B) Λ (A < C); б) (A > B) Λ (A > C);
в) (A < B) Λ (A > C); г) (A > B) V (A > C).
Т 4.4. Любое из чисел X, Y, Z положительно.
Варианты ответа:
а) (X > 0) Λ (Y > 0) V (Z > 0); б) (X > 0) V (Y > 0) Λ (Z > 0);
в) (X > 0) V (Y > 0) V (Z > 0); г) (X > 0) Λ (Y > 0) Λ (Z > 0).
Т 4.5. Любое из чисел X, Y, Z отрицательно.
Варианты ответа:
а) (X < 0) V (Y < 0) V (Z < 0); б) (X > 0) V (Y < 0) Λ (Z < 0);
в) (X < 0) Λ (Y < 0) V (Z < 0); г) (X < 0) Λ (Y < 0) Λ (Z < 0).
Т 4.6. Все числа X, Y, Z равны 12.
Варианты ответа:
а) (X = 12) V (Y = 12) Λ (Z = 12); б) (X = 12) Λ (Y = 12) V (Z = 12);
в) (X = 12) Λ (Y = 12) Λ (Z = 12); г) (X = 12) V (Y = 12) V (Z = 12).
Т 4.7. Только одно из чисел X, Y отрицательно.
Варианты ответа:
а) (X < 0) Λ (Y > 0) Λ (X > 0) Λ (Y < 0); б) (X < 0) V (Y > 0) V (X > 0) Λ (Y < 0);
в) (X < 0) Λ (Y< 0) V (X > 0) Λ (Y < 0); г) (X < 0) Λ (Y > 0) V (X > 0) Λ (Y < 0).
Т 4.8. Какое логическое выражение соответствует высказыванию: «Точка Х принадлежит интервалу (А, В)»?
Варианты ответа:
а) (X < A) или (X > B); б) (X > A) и (X < B);
в) не (X < A) или (X > B); г) (X > A) или (X > B).
Решение логических выражений принято записывать в виде таблиц истинности – таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных.
Для составления таблицы необходимо:
1) выяснить количество строк в таблице (вычисляется как 2n, где n – количество переменных);
2) выяснить количество столбцов = количество переменных + количество логических операций;
3) установить последовательность выполнения логических операций;
4) построить таблицу, указывая названия столбцов и возможные наборы значений исходных переменных;
5) заполнить таблицу истинности по столбцам.
П
4.4. Построим таблицу истинности для выражения F = (A V B) Λ (![]() V
V ![]() ).
).
Количество строк = 22 (2 переменных) + 1(заголовки столбцов) = 5.
Количество столбцов = 2 логические переменные (А, В) + 5 логических операций (V, Λ, - , V, - ) = 7.
Расставим порядок выполнения операций: 1 5 2 4 3
(А V B) Λ ( ![]() V
V ![]() )
)
A |
B |
A V B |
|
|
|
(A V B)Λ( |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Из трех логических операций конъюнкции, дизъюнкции и инверсии (отрицания), выполняемых соответствующими элементами конъюнктром, дизъюнк-
тром и инвертором, можно реализовать любые логические выражения.
А1 1 0 0 |
В1 0 1 0 |
Результат 1 0 0 0 |
А1 1 0 0 |
В1 0 1 0 |
Результат 1 1 1 0 |
А1 0 |
0 1 |
Конъюнктор |
Дизъюнктор |
Инвертор |
|||||
|
|
|
|
|||||
Построение логических схем
Правило построения логических схем:
1) Определить число логических переменных;
2) Определить количество логических операций и их порядок;
3) Изобразить для каждой логической операции соответствующий ей вентиль;
4) Соединить вентили в порядке выполнения логических операций.
П 4.5. Пусть Х = истина, Y = ложь. Составить логическую схему
для следующего логического выражения: F = X ![]() Y
Y ![]() X.
X.
1) Две переменные – X и Y;
2) Две логические операции: 2 1
X ![]() Y
Y![]() X;
X;
3) Строим схему:
 |
|||
 |
|||
Ответ: 1 V 0 Λ 1 = 1.
П 4.6. Построить логическую схему,
соответствующую логическому выражению F = X
![]() Y
Y ![]()
![]() .
Вычислить значения выражения для Х = 1, Y = 0.
.
Вычислить значения выражения для Х = 1, Y = 0.
1) Переменных две: Х и Y;
2) Логических операций три: конъюнкция и две дизъюнкции: 1 4 3 2
X ![]() Y
Y ![]()
![]() ;
;
3) Схему строим слева направо в соответствии с порядком логических операций:
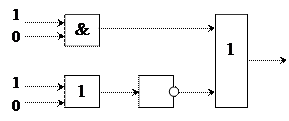 |
4)
Вычислим значение
выражения: F = 1 ![]() 0
0
![]()
![]() =
0.
=
0.
Т 4.9. Составьте таблицы истинности для следующих логических выражений:
1) F = (X ![]()
![]() )
) ![]() Z.
Z.
2) F = X ![]() Y
Y ![]() X.
X.
3) F = ![]()
![]() (Y
(Y ![]() X).
X).
4) F = ![]()
![]() (Z Λ Y).
(Z Λ Y).
Т 4.10. Для какого из указанных значений числа X истинно высказывание:
(X > 4) \/ ((X > 1) → (X > 4))?
а) 1; б) 2; в) 3; г) 4.
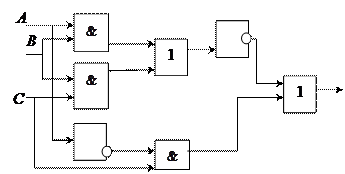
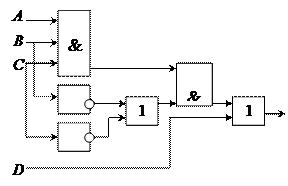
Т 4.11. Постройте логическое выражение по логической схеме:
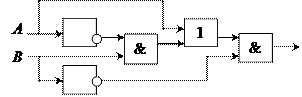
 а)
б)
а)
б)
 |
|||
 |
|||
в) г)
Законы логики
Рассмотрим 6 законов логики и преобразование импликации:
1) коммутативность: A Ú B=B Ú A , A Ù B = B Ù A;
2) ассоциативность: A Ú (B Ú C) = (A Ú B) Ú C,
A Ù (B Ù C) = (A Ù B) Ù C;
3) отрицание операнда: A Ù ![]() =F ,
=F , ![]() Ú A=T ,
Ú A=T , ![]() =A ,
=A , ![]() =T;
=T;
4) дистрибутивность: A Ù (B Ú C) = (A Ù B) Ú (A Ù C),
A Ú (B Ù C) = (A Ú B) Ù (A Ú C);
5) поглощения операнда
A Ú (A ÙB) = A Ù (A Ú B) = А;
6) отрицание формулы (законы де Моргана):
![]() .
.
5) преобразование импликации
A® B = ![]() Ú B.
Ú B.
Законы логики часто используют для упрощения логического выражения.
П 4.7. Упростить логическое выражение ![]() .
.
1) Избавимся от отрицания, используя закон 6 де Моргана
![]() ;
;
2) Применим закон поглощения операнда
к формуле ![]() , тогда
, тогда ![]() .
.
П 4.8. Упростить логическое выражение F = (A→B)![]() (B→A).
(B→A).
1) Избавимся от импликации (A→B) и (B→A), используя преобразование 7
(A→B)![]() (B→A) =
(B→A) = ![]() ;
;
2) Сгруппируем ![]() и применим закон 3 отрицания операнда
и применим закон 3 отрицания операнда
![]() .
.
Т 4.12. а) ![]() .
Т 4.13. а)
.
Т 4.13. а) ![]() ;
;
б) ![]() . б)
. б) ![]() ;
;
в) ![]() в)
в) ![]() .
.
Преобразование высказываний в логическую формулу осуществляется следующим образом:
- выделяют простые высказывания и обозначают их латинскими буквами;
- записывают условия задачи на языке алгебры логики.
П 4.9. Синоптик объявляет прогноз погоды на завтра и утверждает следующее:
1. Если не будет ветра, то будет пасмурная погода без дождя.
2. Если будет дождь, то будет пасмурно и без ветра.
3. Если будет пасмурная погода, то будет дождь и не будет ветра.
Решение:
1. Выделим простые высказывания и запишем их через переменные:
А – «Ветра нет».
В – «Пасмурно».
С – «Дождь».
2. Запишем логические функции (сложные высказывания).
а) «Если не будет ветра, то будет
пасмурная погода без дождя» – ![]() ;
;
б) «Если будет дождь, то будет
пасмурно и без ветра» – ![]() ;
;
в) «Если будет пасмурная погода, то
будет дождь и не будет ветра» – ![]() .
.
Запишите в виде логической формулы следующие высказывания:
Т 4.13. Если Иванов здоров и богат, то он здоров.
Т 4.14. Число является простым, если оно делится только на единицу и само на себя.
Т 4.15. Если число делится на 4, оно делится на 2.
Т 4.16. Произвольно взятое число делится либо на 2, либо делится на 3.
Т 4.17. Спортсмен подлежит дисквалификации, если он некорректно ведет себя по отношению к сопернику или судье, и если он принимал «допинг».
5. АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ
С этой темой можно ознакомиться в главе 5 пособия [1].
Тестовые задачи
Т 5.1. Кто является создателем
языка Pascal?
а) Никлаус Вирт; б) Блез Паскаль; в) Деннис Ритчи; г) Бьерн Страуструп.
Т 5.2. Какая информация известна, если задан тип данных?
а) количество обращений к данным; б) количество записей
данных;
в) начальное
значение; г)
диапазон
возможных значении.
Т 5.3. При выполнении подпрограммы
Алг пр1 (арг цел X, рез цел F)
Нач
если X <= 1
то F:= 2
иначе F: = F * (X – 1) + 3
все
кон
с параметрами (2, А)
значение переменной А будет равно:
а) 5; б) 0; в) 6; г) 2; д) 3.
Т 5.4. Переменная в программе считается полностью заданной, если известны ее:
а) тип, имя; в) тип, значение; б) имя, значение; г) тип, имя, значение.
Т 5.5. Из перечисленных языков программирования
1) ADA; 2) АССЕМБЛЕР; 3) PASСAL; 3) LISP; 4) МАКРОАССЕМБЛЕР
к языкам высокого уровня не относят:
а) 3 и 5; б) 1 и 3; в) 2 и 5; г) только 5; д) только 1.
Т 5.6. После введения значений переменных А, В, С и выполнения фрагмента программы переменная N принимает значение A2.
N=A
IF N > В THEN N = В
IF N < C THEN N = C
N=A*N
Это возможно при следующем соотношении входных переменных:
а) А>B и В>C; б) A<В и А>C; в) А< В и А < С; г) A>B и С < В.
Т 5.7. Первым программистом мира является:
а) Мария Кюри; б) Стив Возняк; в) Билл Гейтс; г) Ада Лавлейс.
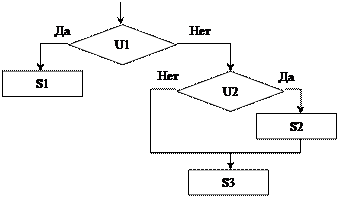 Т 5.8. Дана блок – схема
алгоритма. U1,
U2 обозначают некоторые
условия, а S1,
S2, S3 – операторы. Выбрать
логическое выражение, задающее условие, при котором будет выполняться оператор S3.
Т 5.8. Дана блок – схема
алгоритма. U1,
U2 обозначают некоторые
условия, а S1,
S2, S3 – операторы. Выбрать
логическое выражение, задающее условие, при котором будет выполняться оператор S3.
а) U1 = ложь или U2 = ложь;
б) U1 = ложь ;
в) U2 = ложь или U2 = истина;
г) U1 = ложь или U2 = истина;
д) U2 = истина и U2 = ложь.
6. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ И ТЕХНОЛОГИИ
ПРОГРАММИРОВАНИЯ
С этой темой можно ознакомиться в главе 6 пособия [1].
Тестовые задачи
Т 6.1. Для реализации логики алгоритма и программы, с точки зрения структурного программирования НЕ ДОЛЖНЫ применяться
а) повторение вычислений (циклы); в) ветвления;
б) последовательное выполнение; г) безусловные переходы.
Т 6.2. Виртуальная машина Java является…
а) интерпретатором; в) обработчиком; б) анализатором; г) компилятором.
Т 6.3. Какая стадия трансляции занимается проверкой в выражениях?
а) синтаксический анализ; в) лексический анализ;
б) генерация кодов; г) семантический анализ.
Т 6.4. Программа интерпретатор обеспечивает:
а) поиск файлов на диске;
б) формирование текстового файла;
в) пооператорное выполнение программы;
г) запись машинного кода в виде загрузочного файла.
Т 6.5. Программа-компилятор обеспечивает:
а) перевод исходного текста в машинный код;
б) формирование текстового файла;
в) запись машинного кода в форме загрузочного файла;
г) поиск файлов на дискете.
Т 6.6. Создание исполняемого файла из исходного текста программы предполагает выполнение процессов:
1) компиляции; 2) компоновки; 3) интерпретации; 4) исполнения программы.
Варианты ответов: а) 1, 4; б) 2, 3; в) 1, 2, 3; г) 1, 2.
Т 6.7. Транслятор необходим при программировании на:
а) языке низкого уровня; б) языке машинных команд;
в) языке высокого уровня; г) физическом языке.
Т 6.8. При проектировании программного обеспечения используются подходы:
1) «сверху-вниз»; 2) «снизу-вверх»; 3) «слева-направо»; 4) «справо-налево».
Варианты ответов: а) 1, 4; б) 2, 3; в) 3, 4; г) 1, 2.
7. ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
С этой темой можно ознакомиться в главе 7 пособия [1].
Тестовые задачи
Т 7.1. Среди приведенных отыщите формулу для электронной таблицы:
а) А3В8 + 12; б) А1 = А3*В8 + 12; в) А3*В8 + 12; г) = А3*В8 + 12.
Т 7.2. При перемещении или копировании в электронной таблице абсолютные ссылки:
а) не изменяются;
б) преобразуются вне зависимости от нового положения формулы;
в) преобразуются в зависимости от нового положения формулы;
г) преобразуются в зависимости от длины формулы.
Т 7.3. После копирования формулы из ячейки В1 в ячейку В2 результатом вычисления в ячейке В2 будет:
|
|
A |
B |
C |
|
1 |
2 |
=A1*$C1 |
6 |
|
2 |
3 |
|
7 |
а) 14; б) 10; в) 18; г) 21.
Т 7.4. В электронной таблице выделена группа ячеек А1:В3. Сколько ячеек входит в эту группу?
а) 6; б) 5; в) 3; г) 4.
Т 7.5. После копирования формулы из ячейки В1 в ячейку В2 результатом вычислений в ячейке В2 будет:
|
|
A |
B |
C |
|
1 |
1 |
=ЕСЛИ(A$1>1;5;A1+C$1) |
3 |
|
2 |
2 |
|
4 |
а) 3; б) 4; в) 5; г) 6.
Т 7.6. Каким будет результат в ячейке С2 после буксировки в нее функции из ячейки С1:
|
|
A |
B |
С |
|
1 |
1 |
2 |
=СУММ(A1;B$1) |
|
2 |
3 |
4 |
|
а) 4; б) 5; в) 6; г) 3.
Т 7.7. Представлен фрагмент электронной таблицы в режиме отображения формул.
|
|
А |
В |
|
1 |
1 |
2 |
|
2 |
2 |
|
|
3 |
|
=СЧЕТ(А1:В2;А2) |
Значение в ячейке В3 будет равно
а) 5; б) 3; в) 4; г) 2.
Т 7.8. Дан фрагмент таблицы в режиме отображения формул. Какое числовое значение будет высвечиваться в клетке с адресом В6, если формулу из клетки В2 скопировать в диапазон клеток В3 : В6?
|
|
A |
B |
|
1 |
1 |
=А1 |
|
2 |
2 |
=В1*А$2 |
|
3 |
3 |
|
а) 720; б) 32; в) 120; г) 2; д) 6.
8. БАЗЫ ДАННЫХ
С этой темой можно ознакомиться в главе 8 пособия [1].
Тестовые задачи
Т 8.1. Наиболее точным аналогом реляционной базы данных может служить:
а) неупорядоченное множество данных; б) вектор;
в) генеалогическое дерево; г) двумерная таблица.
Т 8.2. Что из перечисленного не является объектом Access?
а) модули; б) таблицы; в) макросы;
г) ключи; д) формы; е) отчеты;
Т 8.3. Для сохранения программы на языке Visual Basic в СУБД Access используется:
а) модуль; б) таблица; в) отчет; г) форма.
Т 8.4. В таблице базы данных условию запроса:
|
№ п/п |
Страна |
Столица |
Часть света |
Население млн., человек |
Площадь тыс. кв. км |
|
1 |
Австрия |
Вена |
Европа |
7513 |
84 |
|
2 |
Франция |
Париж |
Европа |
53183 |
551 |
|
3 |
Греция |
Афины |
Европа |
9280 |
132 |
|
4 |
Япония |
Токио |
Азия |
114276 |
372 |
|
5 |
США |
Вашингтон |
Америка |
217700 |
9363 |
|
6 |
Афганистан |
Кабул |
Азия |
20340 |
647 |
(Первая_буква (Часть света) = «А») И НЕ((площадь > 700) И (Население > 200000)) удовлетворяют записи: а) 5; б) 4 и 6; в) 4, 5 и 6; г) 4.
Т 8.5. Какую строку будет занимать число 308 после проведения сортировки по возрастанию в полях Фамилия и Предмет?
а) 1; б) 2; в) 3; г) 4.
Фамилия |
Предмет |
Аудитория |
|
Петров |
Химия |
225 |
|
Иванов |
Алгебра |
205 |
|
Иванов |
Геометрия |
111 |
|
Петров |
Биология |
308 |
Т 8.6. Пусть некоторая база данных содержит поля ФАМИЛИЯ, ГОД РОЖДЕНИЯ, ДОХОД. Какая из перечисленных ниже записей этой БД будет найдена при поиске по условию: ГОД РОЖДЕНИЯ>1958 OR ДОХОД<3500
а) Петров, 1956, 3600; в) Сидоров, 1957, 5300;
б) Иванов, 1956, 2400; г) Козлов, 1952, 4200.
Т 8.7. Поле, однозначно идентифицирующее каждую запись в таблице реляционной базы данных, называется:
а) записью; б) ключом; в) отношением; г) доменом.
Т 8.8. Ниже в табличной форме представлен фрагмент базы данных о
результатах тестирования студентов (используется сто балльная шкала):
Фамилия Пол Математика Экология Физика Информатика Экономика
Аганян ж 82 56 46 32 70
Воронин м 43 62 45 74 23
Гришин м 54 74 68 75 83
Роднина ж 71 63 56 82 79
Сергеева ж 33 25 74 38 46
Чернова ж 18 92 83 28 61
Сколько записей в данном фрагменте удовлетворяют условию
«Пол=’м’ ИЛИ Физика>Экономика»?
а) 5; б) 2 в) 3; г) 4.
С этой темой можно ознакомиться в главе 9 пособия [1].
Тестовые задачи
Т 9.1. BBS – это:
а) программа обслуживания сервера организации; б) навигатор;
в) программа для работы и Интернете;
г) система электронных досок объявлений в Интернете.
Т 9.2. Программа The Bat позволяет:
а) архивировать электронную почту; б) загружать веб-страницы;
в) загружать
и редактировать электронную почту.
Т 9.3. HTML (Hyper Text Markup Language) является:
а) сервером Интернета; в) компилятором;
б) средством создания web-страниц; г) локальной сетью.
Т 9.4. Компьютер, подключенный к Интернету, обязательно имеет:
а) IP-адрес; в) домашнюю web-страницу;
б) web-сервер; г) доменное имя.
Т 9.5. Задан адрес электронной почты в сети Интернет: user_name@mtu-net.ru. Имя домена верхнего уровня:
а) ru; б) mtu-net.ru; в) user_name; г) mtu-net.ru.
Т 9.6. В Интернете по протоколу FTP работает:
а) почтовый сервер для
получения сообщений;
б) почтовый сервер для
отправления сообщений;
в) сервер управления обменом
файлами;
г) сервер передачи
гипертекста.
Т 9.7. Сетевой протокол – это:
а) набор соглашений о взаимодействиях в компьютерной сети;
б) последовательная событий, происходящих в компьютерной сети;
в) правила интерпретации данных, передаваемых по сети;
г) правила установления связи между двумя компьютерами в сети;
д) согласование различных процессов во времени.
Т 9.8. Компьютер, предоставляющий свои ресурсы в пользование другим компьютерам при совместной работе, называется:
а) адаптером; в) коммутатором; г) станцией;
б) сервером; д) клиент-сервером.
10. ОСНОВЫ ЗАЩИТЫ ИНФОРМАЦИИ
С этой темой можно ознакомиться в главе 10 пособия [1].
Тестовые задачи
Т 10.1. Сетевые черви это –
а) программы, распространяющиеся только при помощи электронной почты через Интернет
б) программы, которые изменяют файлы на дисках, и распространяются в пределах компьютера;
в) вредоносные программы, действия которых заключается в создании сбоев при питании компьютера от эл. сети;
г) программы, которые не изменяют файлы на дисках, а распространяются в компьютерной сети, проникают в операционную систему компьютера, находят адреса других компьютеров или пользователей и рассылают по этим адресам свои копии.
Т 10.2. Антивирусным пакетом является...
а) PKZIP; б) ARJ; в) WIN.COM; г) DRWEB.
Т 10.3. Сетевые вирусы могут попасть на локальный компьютер:
а) при подключении
к локальной сети;
б) при вводе логина и пароля;
в) при копировании файла с удаленного компьютера;
г) при просмотре web-страницы.
Т 10.4. Загрузочные вирусы характеризуются тем, что:
а) поражают загрузочные сектора дисков;
б) поражают программы в начале их работы;
в) запускаются при загрузке компьютера;
г) изменяют весь код заражаемого файла;
д) всегда меняют начало и длину файла.
Т 10.5. Назначение антивирусных программ под названием детекторы:
а) обнаружение и уничтожение вирусов;
б) контроль возможных путей распространения компьютерных вирусов;
в) обнаружение компьютерных вирусов;
г) “излечение” зараженных файлов;
д) уничтожение зараженных файлов.
Т 10.6. Назначение антивирусных программ под названием доктора:
а) обнаружение и уничтожение вирусов;
б) контроль возможных путей распространения компьютерных вирусов;
в) обнаружение компьютерных вирусов;
г) “излечение” зараженных файлов;
д) уничтожение зараженных файлов.
Т 10.7. К антивирусным программам не относятся:
а) детекторы; б) фильтры; в) ревизоры; г) интерпретаторы;
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.