Лабораторная работа №3

Тема: Транспортная задача линейного программирования

Цель: формирование навыков разработки алгоритма решения транспортной задачи методом потенциалов.

Вид работы: индивидуальный.

Время выполнения: 4 часа.

Теоретический материал

Постановка транспортной задачи

Однородный груз, имеющийся в m пунктах отправления (производства) А1, А2, ..., Аm соответственно в количествах а1, а2, ..., аm единиц, требуется доставить в каждый из n пунктов назначения (потребления) В1, В2, ..., Вn соответственно в количествах b1, b2, ..., bn единиц. Стоимость перевозки (тариф) единицы продукции из Аi в Вj известна для всех маршрутов Ai, Bj и c_ij (i = 1, m; j = 1, n). Требуется составить такой план перевозок, при котором весь груз из пунктов отправления вывозится, и запросы всех пунктов потребления удовлетворяются (закрытая модель), т. е:

а суммарные транспортные расходы минимальны.

Математическая модель транспортной задачи

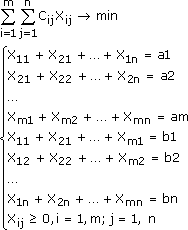
Будем называть любой план перевозок допустимым, если он удовлетворяет системам ограничений и требованиям неотрицательности.

Допустимый план, будем называть опорным, если в нем отличны от нуля не более m+n-1 базисных перевозок, а остальные перевозки равны 0.

План будет называться оптимальным, если он, среди всех допустимых планов, приводит к максимальной суммарной стоимости перевозок.

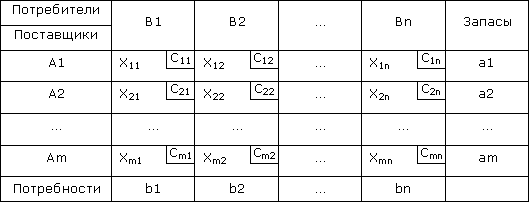
Условия задачи удобно располагать в таблице №4, вписывая в ячейки количество перевозимого груза из Аi в Bj груза X_ij ≥ 0, а в маленькие клетки – соответствующие тарифы C_ij.

Таблица №4

Условия задачи

Затем решение задачи разбивается на два этапа:

1.   Определение опорного плана.

2.   Нахождение оптимального решения путем последовательных операций.

1.    Найдем вначале допустимое (опорное) решение транспортной задачи. Это решение можно найти, используя метод "северо-западного угла" или метод "минимального элемента".

Метод северо-западного угла (диагональный)

Сущность метода заключается в том, что на каждом шаге заполняется левая верхняя (северо-западная) клетка оставшейся части таблицы, причем максимально возможным числом: либо полностью выносится груз из Аi, либо полностью удовлетворяется потребность Вj. Процедура продолжается до тех пор, пока на каком-то шаге не исчерпаются запасы аi и не удовлетворятся все потребности bj. В заключении проверяют, удовлетворяют ли найденные компоненты плана Х_ij горизонтальным и вертикальным уравнениям.

Метод наименьшего элемента

Сущность метода в том, что на каждом шаге заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф; в случае наличия нескольких таких равных тарифов заполняется любая из них. В остальном действуют аналогично предыдущему способу.

2.   Метод потенциалов решения транспортной задачи

Соотношения

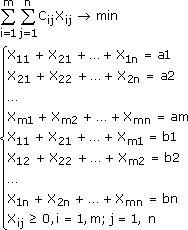
определяют систему из m+n-1 линейных уравнений с m+n известными, имеющую бесчисленное множество решений; для её определённости одному неизвестному присваивают произвольное значение (обычно альфа равное 0), тогда все остальные неизвестные определяются однозначно.

Критерий оптимальности

Если известны потенциалы решения Х0 транспортной задачи и для всех незаполненных ячеек выполняются условия α_i+β_j ≤ C_ij, то Х0 является оптимальным планом транспортной задачи.

Если план не оптимален, то необходимо перейти к следующему плану (таблице) так, чтобы транспортные расходы не увеличивались.

Цикл перерасчёта таблицы – это последовательность ячеек, удовлетворяющая условиям:

1.      Одна ячейка пустая, все остальные занятые.

2.      Любые две соседние ячейки находятся в одной строке или в одном столбце.

3.      Никакие три соседние ячейки не могут быть в одной строке или в одном столбце.

Пустой ячейке присваивают знак "+", остальным – поочерёдно знаки "–" и "+".

Для перераспределения плана перевозок с помощью цикла перерасчёта сначала находят незаполненную ячейку (r, s), в которой αr+βs > Crs, и строят соответствующий цикл; затем в минусовых клетках находят число X = min(X_ij). Далее составляют новую таблицу по следующему правилу:

4.      В плюсовых клетках добавляем Х.

5.      Из минусовых клеток вычитаем Х.

6.      Все остальные клетки вне цикла остаются без изменения.

Получим новую таблицу, дающую новое решение Х, такое, что F (X₁) ≤ F (X₀); оно снова проверяется на оптимальность через конечное число шагов, обязательно найдем оптимальный план транспортной задачи, ибо он всегда существует.

Ход работы:

1. Согласно своему варианту, решить задания без использования  ЭВМ.

2. Написать программу, реализующую алгоритм решения транспортной задачи в соответствии с вариантом.

Задания:

Вариант 1. Четыре предприятия данного экономического района для производства продукции используют три вида сырья. Потребности в сырье каждого из предприятий соответственно равны 120, 50, 190 и 110 ед. Сырье сосредоточено в трех местах его получения, а запасы соответственно равны 160, 140 и 170 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются матрицей:

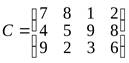
Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.

Вариант 2. Для строительства трех объектов используется кирпич, изготовляемый на трех заводах. Ежедневно каждый из заводов может изготовлять 100, 150 и 50 ус. ед. кирпича. Ежедневные потребности в кирпиче на каждом из строящихся объектов соответственно равны 75, 80, 60 и 85 усл. ед. Известны также тарифы перевозок 1 усл. ед. кирпича с каждого завода к каждому из строящихся объектов и задаются матрицей:

Составить такой план перевозок кирпича, при котором общая стоимость перевозок является минимальной.

Вариант 3. Сельскохозяйственный кооператив «Ласточка» в области имеет три филиала Ф1, Ф2 и Ф3, которые обеспечивают поставками подсолнечных семян в соответствии с заявками пять заводов производителей подсолнечного масла  А, В, С, D и Е. Объемы запасов семян, объемы заказов на поставку и тарифы на перевозку приведены в транспортной таблице №5.

Таблица №5

Условия задачи

Построить оптимальный план перевозки подсолнечных семян с минимальными транспортными расходами

Вариант 4. Фирма «Союз» обеспечивает доставку видео- и аудиокассет с четырех складов, расположенных в разных точках города в четыре магазина. Запас кассет, имеющихся на складах, а также объемы заказов магазинов и тарифы на доставку представлены в транспортной таблице №6.

Таблица №6

Условия задачи

Определить  объемы перевозок, обеспечивающих их минимальные затраты.

Вариант 5. Московский филиал фирмы «The Coca-Cola Company», выпускающей газированные напитки приблизительно равного спроса (Sprite, Coca-Cola, Fanta), складируемые в разных местах, должен поставить свою продукцию в четыре крупных московских супермаркета: «Рамстор-1», «Рамстор-2». «Седьмой Континент», супермаркет «Арбатский».

Каждая упаковка содержит 12 банок емкостью 0,33 литра. Тарифы на доставку товара, объемы запасов и заказы на продукцию приведены в таблице №7.

Таблица №7

Условия задачи

Определить оптимальный план поставок газированных напитков в супермаркеты города, а также затраты на перевозку.

Вариант 6. Автотранспортная компания «Астрада» обеспечивает доставку шин «Bridgestone» с трех оптовых складов, расположенных в Москве, Нижнем Новгороде и Покрове в пять магазинов в Чебоксарах, Нижнем Новгороде, Вязниках, Набережных челнах и Казани. Объемы запасов шин на складах, объемы заявок магазинов и тарифы на перевозку приведены в транспортной таблице №8.

Таблица №8

Условия задачи

Составить оптимальный план, обеспечивающий минимальные транспортные расходы перевозок.

Вариант 7. Фирма «Московия» заключила контракт с компанией АЛРОСА (Алмазы России — Саха) на покупку промышленного золота для его реализации в пяти городах в объемах: Самара — 80 кг, Москва — 260 кг, Ростов-на-Дону — 100 кг, Санкт-Петербург — 140 кг. Нижний Новгород — 120 кг.

Компания располагает тремя месторождениями «Мирное», «Удачный» и «Полевое», которые планируют за год выработать соответственно 200, 250 и 250 кг золота.

Определить минимальную стоимость фрахта специализированного транспорта, обеспечивающую полное удовлетворение заявок покупателей, при заданной матрице тарифов.

        7 9 15 4 18

С = 13 25 8 15 5

        5 11 6 20 12

Вариант 8. Составить оптимальный план перевозки автомобилей из городов Ижевск, Казань, Тольятти в города Москва, Саранск и Ульяновск. Стоимость перевозки одного автомобиля составляет 10 руб. за км. Расстояние между городами, объемы заявок и заказов представлены в таблице №9.

Таблица №9

Условия задачи

Составить оптимальный план перевозок, обеспечивающий минимальные затраты на перевозку.

Вариант 9. Составить оптимальный план перевозки лекарств с минимальными затратами из аптечных складов в пять аптек города: больница №15, городские клинические больницы № 7, № 23 и № 50 и институт им. Бурденко. Запасы лекарств на складах, заявки потребителей и тарифы перевозок представлены в таблице №10.

Таблица №10

Условия задачи

Вариант 10. Составить оптимальный план перевозки угля с минимальными транспортными расходами с шахт Варгашорская (В). Западная (3) и Комсомольская (К), еженедельно добывающих соответственно 26, 32 и 17 тыс. т. Покупатели угля расположены в разных городах А, В, С и D, заявки которых составляют 28,19,12 и 16 тыс. т соответственно. Тарифы, определяющие стоимость перевозки 1 тыс. т между поставщиками и потребителями представлены в транспортной таблице №11.

Таблица №11

Условия задачи

Вариант 11. Составьте оптимальный план завоза хлебобулочной продукции с минимальными транспортными расходами из трех пекарен фирмы «Колос» в четыре булочных города: А, В, С, D. Заказы на поставку хлебобулочных изделий, производительность пекарен и транспортные тарифы представлены в транспортной таблице №12.

Таблица №12

Условия задачи

Контрольные вопросы:

1.      Дайте определение транспортной задаче.

2.      Этапы решения транспортной задачи.

3.      Отличие метода "северо-западного угла" от метода "минимального элемента".

Скачано с www.znanio.ru