


Основные свойства тригонометрических функций
|
|
y= sin x |
y=cosx |
|
Область определения |
(−;+) |
(−;+) |
|
Множество значений |
−1;1 |
−1;1 |
|
Четность |
нечетная |
четная |
|
Периодичность (основной период) |
2 |
2 |
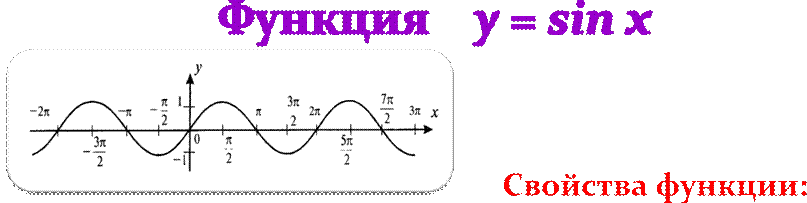
1. D(sin x) = R
2. y = sin x – нечетная функция, график симметричен относительно начала координат
3. периодичноть: T = 2π
4. sin x = 0 при х = πn, nZ (нули функции) 5. промежутки знакопостоянства:
sin x > 0 при 0 + 2πn < x < π+ 2πn, nZ sin x < 0 при π + 2πn < x < 2π+ 2πn, nZ
6. промежутки монотонности:
x[-π/2 + 2πn; π /2 + 2πn], nZ – возрастает
x[π/2 + 2πn; 3π/2 + 2πn], nZ– убывает
7. экстремумы:
y max = 1 при х = π/2 + 2πn, nZ
y min = - 1 при х = -π/2 + 2πn, nZ
8. E(sin x) = [- 1 ; 1]
 Построение
функции y = sin x ±b
Построение
функции y = sin x ±b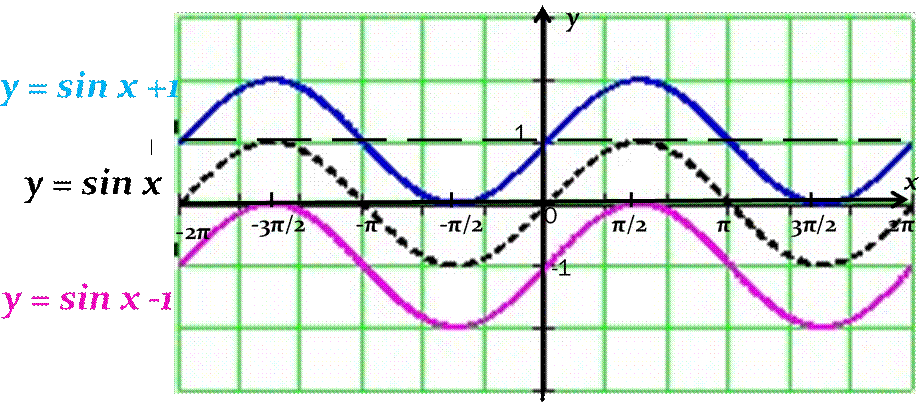
 Построение
функции y = sin x ±b
Построение
функции y = sin x ±b


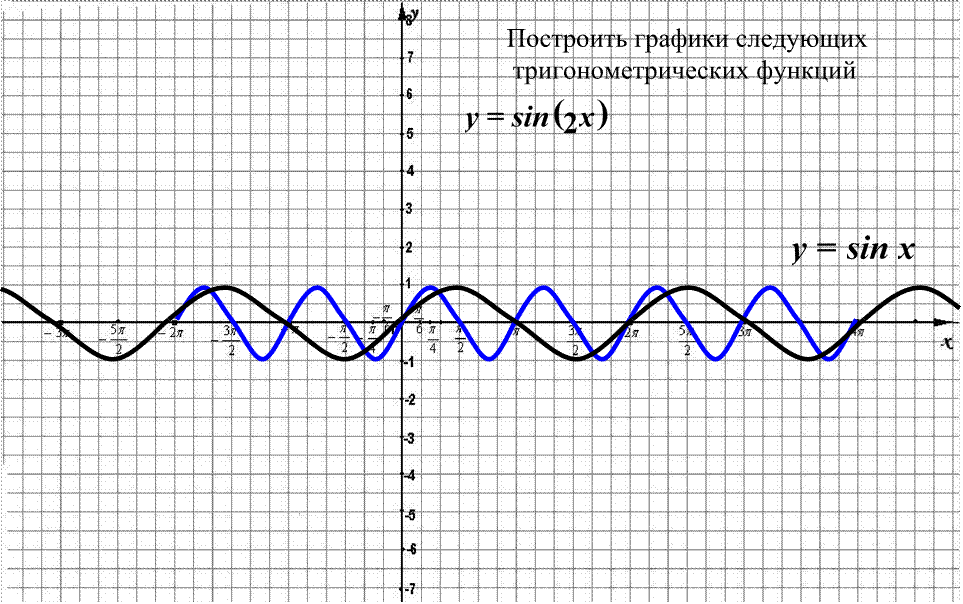
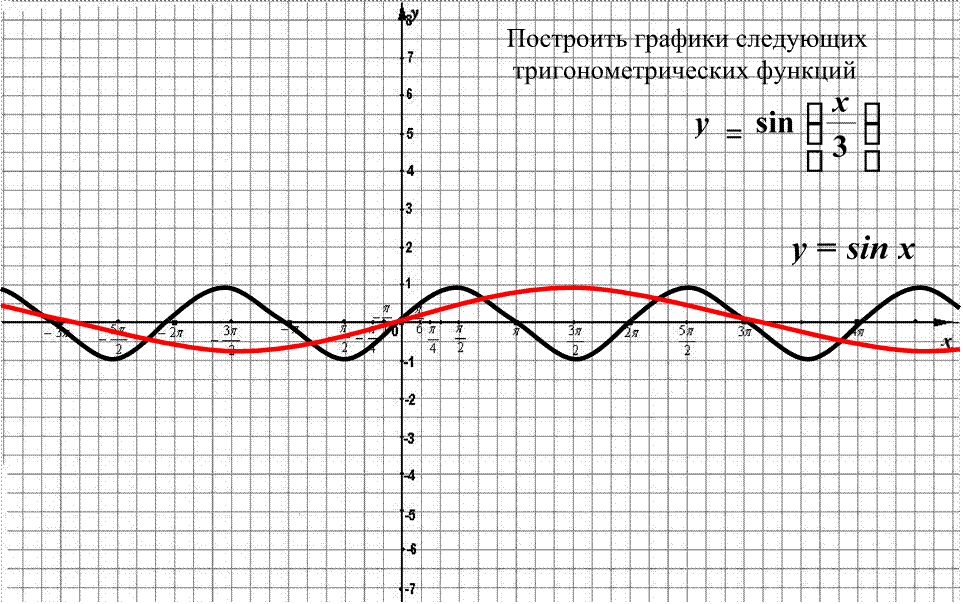
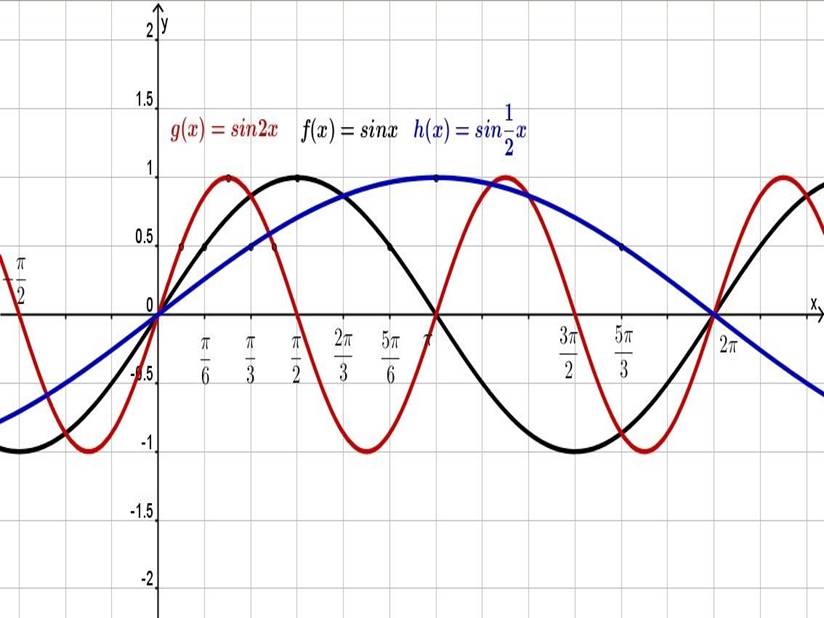
Растяжение (сжатие) в k раз вдоль оси OX (оси
абсцисс)
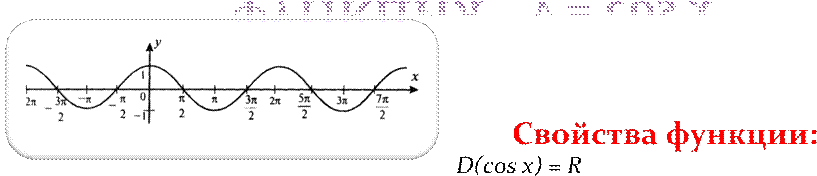 ФУНКЦИЯ y = cos x
ФУНКЦИЯ y = cos x
1.
График функции y = cos x 2. y = cos x – четная функция, график симметричен относительно оси ординат
3. периодичноть: T = 2π
4. cos x = 0 при х = π/2 + πn, nZ (нули функции) 5. промежутки знакопостоянства:
cos x > 0 при -π /2 + 2πn < x < π/2 + 2πn, nZ cos x < 0 при π/2 + 2πn < x < 3π/2 + 2πn, nZ
6. промежутки монотонности: x[ π+ 2πn; 2π+ 2πn], nZ – возрастает
x[0 + 2πn; π+ 2πn], nZ– убывает
7. экстремумы:
y max = 1 при х = 2πn, nZ
y min = - 1 при х = π+ 2πn, nZ
8. E(cos x) = [- 1 ; 1]
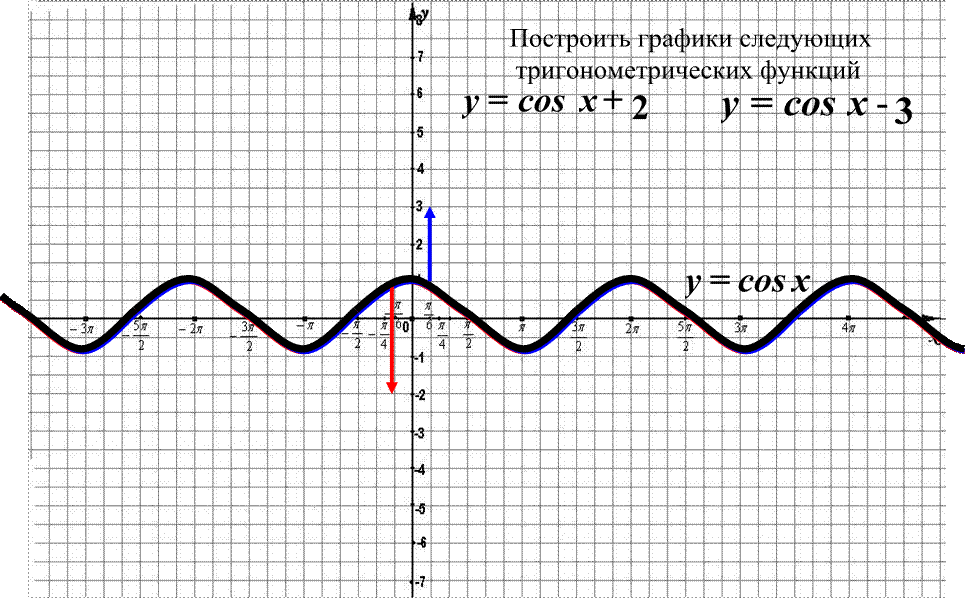
Параллельный перенос вдоль оси OY (оси ординат)
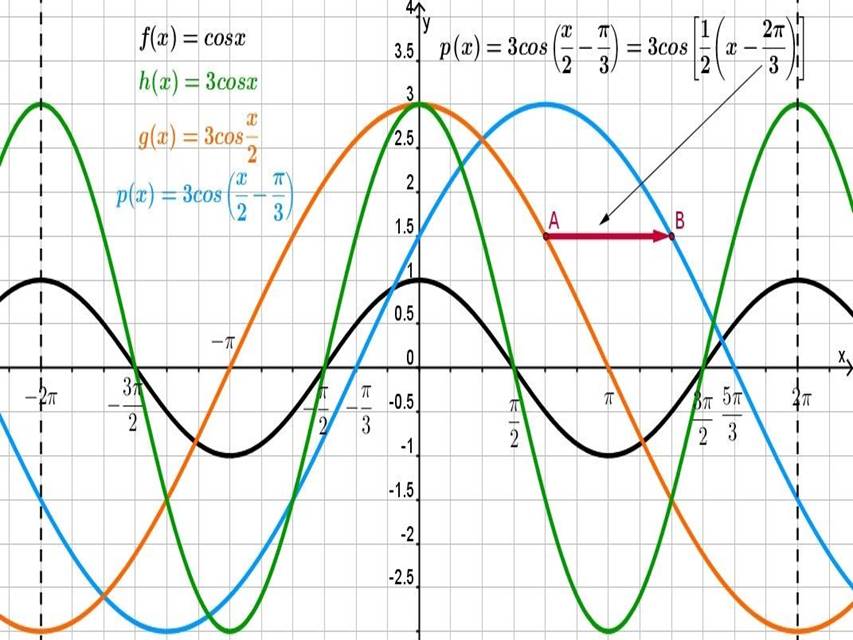
 Построение
функции y = cos(x ±π/2)
Построение
функции y = cos(x ±π/2)



Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.