Тригонометрические функции и их графики

Тема «Тригонометрические функции и их графики»

Перепишите конспект и аккуратно постройте графики.

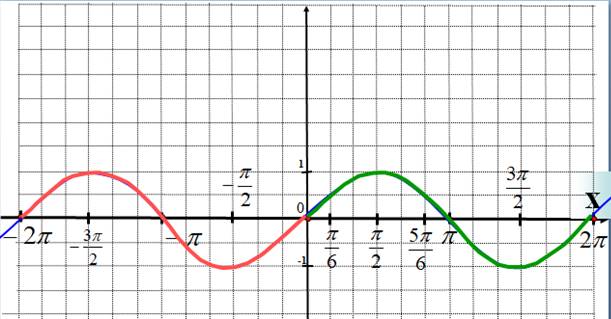
1. Функция синус и ее график

Рассмотрим функцию .

Основные свойства этой функции:

1) Область определения ;

2) Область значений ;

3) Функция нечетная ;

4) Функция не является монотонной на всей своей области определения;

5) Функция периодична с периодом .

Построим график функции . При этом удобно начинать построение с изображения области, которая ограничивает графика сверху числом 1 и снизу числом -1, что связано с областью значений функции. Кроме того, для построения полезно помнить значения синусов нескольких основных табличных углов, например, что  Это позволит построить первую полную «волну» графика и потом перерисовывать ее вправо и влево, пользуясь тем, что картинка будет повторяться со смещением на период, т.е. на .

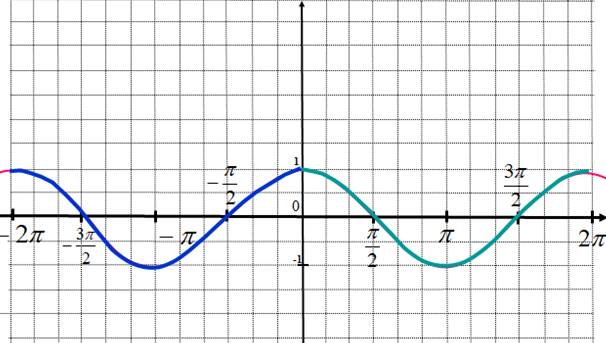
2. Функция косинус и ее график

Теперь рассмотрим функцию

Основные свойства этой функции:

1) Область определения ;

2) Область значений ;

3) Функция четная  Из этого следует симметричность графика функции относительно оси ординат;

4) Функция не является монотонной на всей своей области определения;

5) Функция периодична с периодом .

Построим график функции . Как и при построении синуса удобно начинать с изображения области, которая ограничивает график сверху числом 1 и снизу числом -1, что связано с областью значений функции. Также нанесем на график координаты нескольких точек, для чего необходимо помнить значения косинусов нескольких основных табличных углов, например, что  С помощью этих точек мы можем построить первую полную «волну» графика и потом перерисовывать ее вправо и влево, пользуясь тем, что картинка будет повторяться со смещением на период, т.е. на .

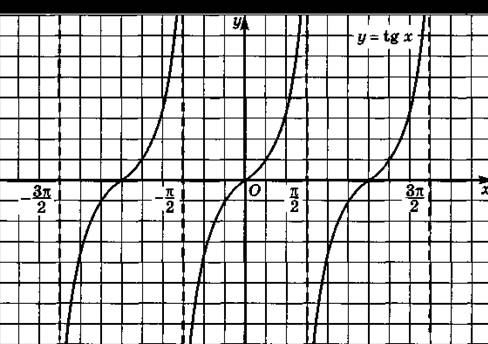
3. Функция тангенс и ее график

Перейдем к функции

Основные свойства этой функции:

1) Область определения  кроме , где .

2) Область значений , т.е. значения тангенса не ограничены;

3) Функция нечетная ;

4) Функция монотонно возрастает в пределах своих так называемых веток тангенса, которые мы сейчас увидим на рисунке;

5) Функция периодична с периодом 

Построим график функции . При этом удобно начинать построение с изображения вертикальных асимптот графика в точках, которые не входят в область определения, т.е.  и т.д. Далее изображаем ветки тангенса внутри каждой из образованных асимптотами полосок, прижимая их к левой асимптоте и к правой. При этом не забываем, что каждая ветка монотонно возрастает. Все ветки изображаем одинаково, т.к. функция имеет период, равный . Это видно по тому, что каждая ветка получается смещением соседней на  вдоль оси абсцисс.

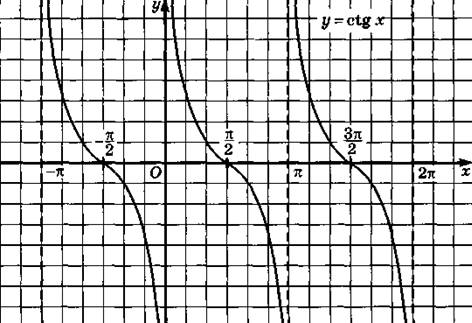
4. Функция котангенс и ее график

И завершаем рассмотрением функции

Основные свойства этой функции:

1) Область определения  кроме , где .

2) Область значений , т.е. значения котангенса не ограничены;

3) Функция нечетная ;

4) Функция монотонно убывает в пределах своих веток, которые похожи на ветки тангенса;

5) Функция периодична с периодом 

Построим график функции . При этом, как и для тангенса, удобно начинать построение с изображения вертикальных асимптот графика в точках, которые не входят в область определения, т.е.  и т.д. Далее изображаем ветки котангенса внутри каждой из образованных асимптотами полосок, прижимая их к левой асимптоте и к правой. В этом случае учитываем, что каждая ветка монотонно убывает. Все ветки аналогично тангенсу изображаем одинаково, т.к. функция имеет период, равный .

Скачано с www.znanio.ru