Тригонометрические функции и их свойства

План урока

1.      Повторение:

Область определения функции

Множество всех значений, которые принимает аргумент (т.е. х) функции, называется областью определения функции и обозначается  D (f) или D (y).

Например:

 1. D (у): (- ∞; 0) и (0;+∞) всё множество действительных чисел, кроме нуля.

2. D (у): ( -∞; +∞) всё мн-во действит.чисел

3. D (у): ( -∞; 0] всё мн-во действит. отриц.чисел

4. D (у):[0; +∞) мн-во неотрицат.чисел

Множество значений функции

Множество всех значений, которые может принять зависимая переменная (т.е. у), называется множеством или областью значения функции и обозначается E (f) или E (y).

Например:

1. Е (у): ( -∞; 0) и (0;+∞) всё множество действительных чисел, кроме нуля.

2. Е (у): [0; +∞) мн-во неотрицат.чисел

3. Е (у):(- ∞; +∞) всё мн-во действит.чисел 

4. Е (у): ( -∞; 0] мн-во отрицат.чисел

2. Пройди по ссылке

https://www.youtube.com/watch?v=aRJYpokr5ZM

3.С помощью текста заполнить таблицу:

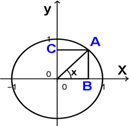Каждому действительному числу x соответствует единственная точка единичной окружности,  получаемая поворотом точки (1;0) на угол x радиан.

Для этого угла определены sin x и cos x. Тем самым каждому действительному числу x поставлены в соответствие числа sin x и cos x, т.е. на множестве R всех действительных чисел определены функции

y = sin x и y = cos x

Таким образом:

областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.

Чтобы найти множество значений функции y = sin x и y = cos x , нужно выяснить, какие значения может принимать y при различных значениях x, т.е. установить, для каких значений y есть такие значения x, при которых sin x = y. Известно, что уравнения sin x = a и cos x  = a имеет корни, если |a| ≤ 1, и не имеет корней, если |a| >1.
Следовательно:

Множеством значений функции y = sin x и y = cos x  является отрезок -1 ≤ y ≤ 1.

Функция y = tg x определяется формулой y = tg x = sin x/cos x. Эта функция определена при тех значениях x, для которых cos x ≠ 0. Известно, что cos x = 0 при x = π/2 + πk, k Є Z.
Следовательно:

3.областью определения функции y = tg x является множество чисел x ≠ π/2 + πk, k Є Z.
Так как уравнение tg x = a имеет корни при любом действительном значении a, значит

4.множеством значений функции y = tg x является множество R всех действительных чисел.

Функции y = sin x, y = cos x, y = tg x называют тригонометрическими функциями.

4. Закрепление.  Выполни задания письменно в тетради

1.Найдите область определения функции:

а)  ;                             

б)  ;

в)  
г)  .

2. Найдите множество значений функции:

 а) ;

б) 

 в)  ;

г)  

5. Вышли свою работу учителю

Скачано с www.znanio.ru