Центральные и вписанные углы

Тема. Центральные и вписанные углы

рис1                              рис2.                                                                                               рис3

Устно. Вспомните, что называется окружностью? Что называется ради­усом диаметром, хордой. Какая прямая называется касательной?

Задание 1. Постройте в тетради окружность и все названные элементы рис1. Назовите  радиусы окруж­ности. Сколько можно провести радиу­сов, диаметров, хорд в окружности? При построении этих элементов ок­ружности у нас получились углы. Назовите их.

Внимание вопрос!  Вспомните, что вы знаете о паре углов AOC и BOA.. Как называется угол ВОС?  Что является сторонами этих углов? А вершины углов где расположены?  А угол BCD - он какой?  Чем являются стороны этого угла?

 Задание 2.  Выпишите углы с вершиной в точке О.

Внимание вопрос. Чем является точка О? Какие отрезки являются сторонами углов?

Вывод. Такие углы называются центральными. Запишем определение в тетрадь.

Проблема! Все ли названы углы с вершиной в точке О? «Градусная мера центрального угла равна градусной мере дуги на которую он опирается». Дуга CВ  называется полуокружностью. Тогда вся ок­ружность имеет градусную меру 360°. Если дана градусная мера одного из центральных углов можно найти другие углы. Рис2. Закрепление.

  Мы возвращаемся к рисунку 1

Угол CBD не является центральным, его вершина располо­жена на окружности, а стороны являют­ся хордами. Этот угол имеет свое назва­ние - вписанный. Запишите определение.

  «Угол, вершина которого лежит на окружности, а сто­роны пересекают окружность, называется впи­санным.»

 Начертите рис3. На­зовите вписанный угол: его вершину и стороны. По аналогии с центральным углом вписанному углу тоже соответ­ствует определенная дуга. Назовите ее.  CAB - вписанный угол, А - вершина угла. - АС и АВ - стороны (хорды). - Угол CAB опирается на дугу С ДВ.

Проблема! Назовите центральные углы? На какую дугу он опирается?

Вывод! Вписанный угол измеряется полови­ной дуги, на которую он опирается (или половиной центрального угла).

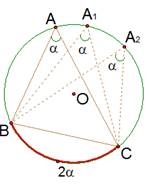
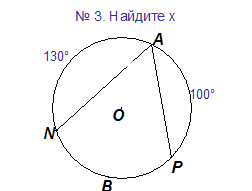
Следствие 1: Вписанные углы, опирающиеся на одну и ту же дугу, равны между собой (см. Рис. 4).

                         Рис4                                                    рис5                                               рис6                                       

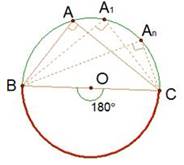
Следствие 2: Вписанные углы, опирающиеся на диаметр, прямые (см. Рис. 5).

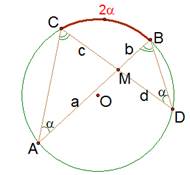
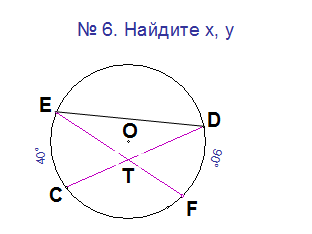
Теорема о хордах. Если две хорды пересекаются, то произведение отрезков одной хорды равны произведению отрезков другой хорды. ВМ*МА=СМ*МД.

 Проверка знаний .

 Вариант I. Вместо многоточия вставьте верный вариант ответа: в 2 раза больше; в 2 раза меньше; равно.

     1. Вписанный в окружность угол всегда…………………соответствующего центрального угла.

     2. Центральный угол всегда………………соответствующей дуге.

     3. Вписанный в окружность угол всегда…………соответствующей дуги.

     4. Центральный угол всегда…………соответствующего вписанного угла.

     5. Дуга окружности всегда……………соответствующего вписанного угла.

     6. Градусная мера дуги всегда……………….соответствующему центральному углу.

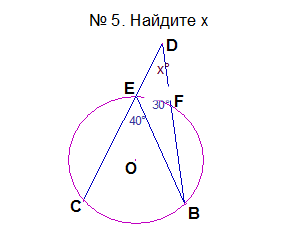
Проверка знаний .

Вариант II.  Вместо многоточия вставьте верный вариант ответа: в 2 раза больше; в 2 раза меньше; равно.

1. Градусная мера дуги всегда………...соответствующему центральному углу.

2. Центральный угол всегда…………...соответствующей дуге.

     3. дуга окружности всегда………………..соответствующего вписанного угла.

     4. Центральный угол всегда………………соответствующего вписанного угла.

     5. Вписанной в окружность угол всегда…………………соответствующей дуги.

     6. Вписанный в окружность угол всегда…………………..соответствующего центрального угла.

Скачано с www.znanio.ru