
ЦЕПНЫЕ ДРОБИ
Оглавление
Введение
Глава I. Правильные конечные цепные дроби
§1.1. Представление рациональных чисел цепными дробями
§1.2. Подходящие дроби
Глава II. Бесконечные цепные дроби
§2.1. Разложение действительного иррационального числа в правильную бесконечную цепную дробь
§2.2. Сходимость правильных бесконечных цепных дробей
§2.3. Практическое применение цепных дробей
Заключение
Список литературы
Вопрос о теории цепных дробей является одним из древнейших математических вопросов, а теория цепных дробей, в свою очередь, одной из первых в математике.
В свою очередь, что же называется
цепной дробью? В качестве примера можно рассмотреть дробь ![]() . Наибольшим целым числом, при этом
не превосходящим данной дроби является 1:
. Наибольшим целым числом, при этом
не превосходящим данной дроби является 1:
![]()
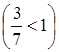 .
.
Далее перевернем дробь ![]() :
:
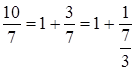 .
.
Наибольшим целым числом, при этом не
превосходящим дроби ![]() является 2. Таким
образом, получаем:
является 2. Таким
образом, получаем:
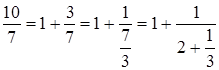 .
.
Это и называется цепной дробью для
дроби ![]() . Таким же образом можно представлять все числа. Если
число является иррациональным, то данный процесс будет продолжаться бесконечно.
Если же число является рациональным, то дробь такого вида будет конечна.
. Таким же образом можно представлять все числа. Если
число является иррациональным, то данный процесс будет продолжаться бесконечно.
Если же число является рациональным, то дробь такого вида будет конечна.
Теорией цепных дробей занимался итальянский математик Рафаэль Бомбелли. Именно он в 1572 году ввел данное понятие. Так же начало современной теории цепных дробей было положено Пьетро Антонио Катальди в 1613 году. Данный ученый отметил их основное свойство ˗ положение между подходящими дробями, а так же и ввёл обозначение, которое напоминает современное. Позднее его теория была расширена Джоном Валлисом, которым и был предложен термин «непрерывная дробь». В конце XVIII века появился эквивалентный термин «цепная дробь».
Цепными дробями однозначно отображаются действительные числа. Таким образом, зная цепную дробь, которая изображает действительное число, можно определить само это число с достаточной точностью. В этом и заключается основное значение такого изображения. Именно поэтому тема курсовой работы достаточно актуальна.
Цель работы: изучить современные подходы к исследованию цепных дробей и систематизировать изученный материал.
В соответствии с целью были поставлены следующие задачи:
1. найти материал по данной теме в учебных и научных источниках;
2. определить понятие цепной дроби;
3. рассмотреть теорию правильных конечных цепных дробей и бесконечных цепных дробей;
4. проанализировать изученную литературу;
5. систематизировать и изложить материал в форме курсовой работы.
Основное содержание курсовой работы описано в двух главах и, соответственно, в 5 параграфах, в которых приведены основные понятия и утверждения, которые касаются теории цепных дробей. Так же приведена практическая часть, где можно увидеть задачи и примеры, касающиеся практического применения цепных дробей, а так же показывающая их применение в жизни.
Целое число ![]() называется общим делителем целых
чисел
называется общим делителем целых
чисел ![]() , если
, если ![]() Целое
число
Целое
число ![]() называется наибольшим
общим делителем чисел
называется наибольшим
общим делителем чисел ![]() , если:
, если:
1) ![]() -
общий делитель;
-
общий делитель;
2) ![]() где
где ![]() -
любой общий делитель чисел
-
любой общий делитель чисел ![]() .
.
Как правило, в качестве наибольшего общего делителя рассматриваются только положительные числа [3, c.50].
Наибольший общий делитель
обозначается ![]()
Пусть ![]() - рациональное число, причем b>0. Применив к a и b алгоритм Евклида для определения их
наибольшего общего делителя.
- рациональное число, причем b>0. Применив к a и b алгоритм Евклида для определения их
наибольшего общего делителя.
1) Разделим ![]() на
на
![]() с остатком:
с остатком: ![]()
2) Разделим ![]() на
на
![]() с
остатком:
с
остатком: ![]()
Продолжая процесс и так далее, получаем конечную систему равенств:
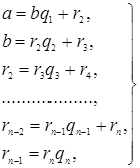 (1)
(1)
где
неполным частным последовательных делений ![]() соответствуют остатки
соответствуют остатки ![]() с
условием
с
условием ![]() .
.
Системе равенств (1) соответствует равносильная система
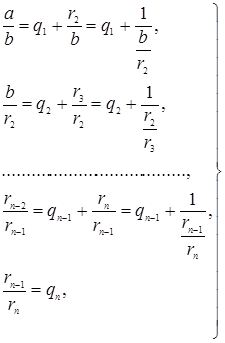 (2)
(2)
из которой
последовательной заменой каждой из дробей ![]() и т.д. ее соответствующим выражением из следующей строки
получается представление дроби
и т.д. ее соответствующим выражением из следующей строки
получается представление дроби ![]() в виде:
в виде:
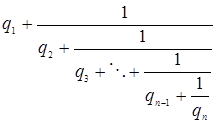
Такое выражение
называется правильной (конечной) цепной или правильной непрерывной дробью, при
этом предполагается, что ![]() – целое число, а
– целое число, а ![]() - натуральные числа [5, c.320].
- натуральные числа [5, c.320].
Имеются различные формы записи цепных дробей:
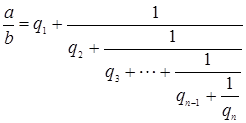 ,
,
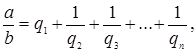
![]()
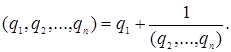
Числа ![]() называются элементами цепной
дроби.
называются элементами цепной
дроби.
Найти представление любого рационального числа в виде цепной дроби дает возможность алгоритм Евклида. В качестве элементов цепной дроби получаются неполные частные последовательных делений в системе равенств (1), именно поэтому элементы цепной дроби называются также неполными частными. Кроме того, равенства системы (2) показывают, что процесс разложения в цепную дробь состоит в последовательном выделении целой части и перевертывании дробной части [1, c.120].
Последняя точка зрения является более общей по сравнению с первой, так как она применима к разложению в непрерывную дробь не только рационального, но и любого действительного числа.
Так как алгоритм Евклида последовательного деления ![]() на
на ![]() является
конечным, то разложение рационального числа
является
конечным, то разложение рационального числа ![]() имеет, очевидно,
конечное число элементов [4, c.24].
имеет, очевидно,
конечное число элементов [4, c.24].
Каждая цепная дробь представляет определенное
рациональное число, то есть равна определенному рациональному числу. Но
возникает следующий вопрос: «Не имеются ли различные представления одного и
того же рационального числа цепной дробью?» Оказывается, что не имеются, если
потребовать, чтобы было ![]() .
.
Теорема. Существует одна и
только одна конечная цепная дробь, равная данному рациональному числу, но при
условии, что ![]() .
.
Доказательство: 1) Заметим, что при уклонении
от указанного условия единственность представления не выполняется.
Действительно, при ![]() :
:
![]()
так что представление можно увеличить:
![]()
например, (2, 3, 1, 4, 2) = ( 2, 3, 1, 4, 1, 1).
2) Принимая условие ![]() ,
можно утверждать, что целая часть цепной дроби
,
можно утверждать, что целая часть цепной дроби ![]() равна ее первому
неполному частному
равна ее первому
неполному частному ![]() . Действительно:
. Действительно:
1. При n=1 процесс очевиден;
2.
При
n=2 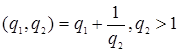 ; поэтому
; поэтому ![]()
3. При n>2
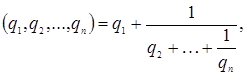 где
где 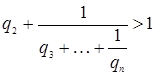 , т.к.
, т.к. ![]()
Поэтому и здесь ![]() .
.
Докажем, что рациональное число ![]() однозначно
представляется цепной дробью
однозначно
представляется цепной дробью ![]() , при условии, если
, при условии, если ![]() .
.
Пусть ![]() с
условием
с
условием ![]() ,
, ![]() . Тогда
. Тогда 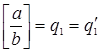 , так что
, так что ![]() . Повторным сравнением целых частей
получаем
. Повторным сравнением целых частей
получаем ![]() , следовательно
, следовательно ![]() и так далее. Если
и так далее. Если ![]() , то в продолжении указанного
процесса получим также
, то в продолжении указанного
процесса получим также ![]() . Если же
. Если же ![]() , например
, например ![]() , то получим
, то получим 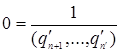 , что невозможно.
, что невозможно.
Теорема доказана [9, c.534].
Вместе с тем было установлено, что при соблюдении
условия ![]() между рациональными
числами и конечными цепными дробями существует взаимно однозначное
соответствие.
между рациональными
числами и конечными цепными дробями существует взаимно однозначное
соответствие.
Замечания:
1.
В
случае разложения правильной положительной дроби первый элемент ![]() , например,
, например, 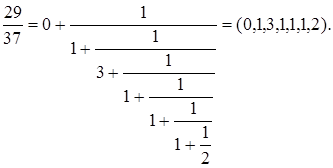
2. При разложении отрицательной дроби (отрицательный знак дроби всегда относится к числителю) первый элемент будет отрицательным, остальные положительными, так как целая часть отрицательной дроби является целым отрицательным числом, а ее дробная часть, как всегда, положительна [13, c. 112].
Пример:
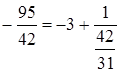 , а
так как
, а
так как ![]() , то
, то ![]() [18, c.51].
[18, c.51].
3. Всякое целое число можно рассматривать как непрерывную дробь, которая состоит из одного элемента.
Пример: 5=(5); ![]() .
.
Задача обращения или свертывания цепной дроби ![]() в простую дробь
в простую дробь ![]() противостоит задаче разложения
обыкновенной дроби в непрерывную дробь.
противостоит задаче разложения
обыкновенной дроби в непрерывную дробь.
Определение: Если процесс построения конечной цепной дроби остановить на некотором шаге, то мы получим дробь, которая называется подходящей дробью [17, c.57].
При этом основную роль играют дроби следующего вида:
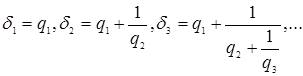 или
или
![]() которые
и называются подходящими дробями данной непрерывной дроби или соответствующего
ей числа
которые
и называются подходящими дробями данной непрерывной дроби или соответствующего
ей числа ![]() .
.
Заметим, что ![]() =
=![]() =
=![]() . Считается, что
подходящая дробь
. Считается, что
подходящая дробь ![]() имеет
порядок k.
имеет
порядок k.
Прежде чем приступить к вычислению подходящих дробей, необходимо
заметить, что ![]() переходит
в
переходит
в ![]() ,
если в первой заменить
,
если в первой заменить ![]() выражением
выражением 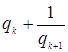 .
.
Имеем 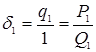 ,
,
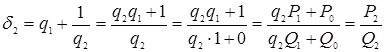 ,
,
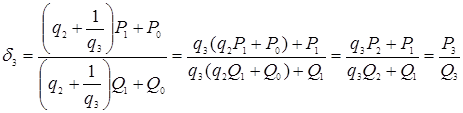 , …,
, …,
при этом принимается, что ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() и так далее.
и так далее.
Закономерность, которую можно заметить в построении
формулы для ![]() (ее числителя
(ее числителя ![]() и знаменателя
и знаменателя ![]() ), сохраняется при переходе к
), сохраняется при переходе к ![]() и сохранится также при переходе от
k к (k+1).
и сохранится также при переходе от
k к (k+1).
Поэтому, воспользовавшись методом математической
индукции, для любого k,
где ![]() ,
имеем
,
имеем
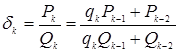 ,
(1)
,
(1)
причем
![]() (2)
(2)
![]() (3)
(3)
Далее, говоря о подходящих дробях ![]() (в свернутом виде), будем иметь в
виду их форму
(в свернутом виде), будем иметь в
виду их форму ![]() [16, c.300].
[16, c.300].
Соотношения (1) являются рекуррентными формулами для
вычисления подходящих дробей, а также их числителей и знаменателей. Из формул
для числителя и знаменателя можно сразу увидеть, что при увеличении k
они возрастают. Последовательное вычисление числителей ![]() и знаменателей
и знаменателей ![]() подходящих дробей по
формулам (2) и (3) удобно располагать по схеме:
подходящих дробей по
формулам (2) и (3) удобно располагать по схеме:
|
|
|
|
|
… |
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
… |
|
Теорема 1:
При ![]() числитель
и знаменатель двух соседних дробей связаны соотношением:
числитель
и знаменатель двух соседних дробей связаны соотношением: ![]() [14, c.320].
[14, c.320].
Доказательство: Проведем индукцию по k:
1)
При
k=1 равенство справедливо, так как ![]()
![]() .
.
2)
Пусть
это равенство верно при некотором k=n
(![]() ).
).
3) Докажем справедливость равенства при k=n+1.
![]()
![]() , то есть равенство верно
при k=n+1.
, то есть равенство верно
при k=n+1.
Согласно принципу полной математической индукции
равенство верно для всех k(![]() ).
).
Теорема 2:
Числитель и знаменатель любой подходящей дроби – взаимно простые числа, то есть всякая k–подходящая дробь несократима [19, c.32].
Доказательство: Докажем это свойство методом от
противного. По предыдущему свойству имеем ![]() .
.
Пусть ![]() , то
есть
, то
есть ![]() ,
тогда из равенства
,
тогда из равенства 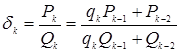 следует, что
следует, что ![]() делится на
делится на ![]() без остатка, что невозможно.
Значит, наше допущение неверно, а верно то, что требовалось доказать, то есть
без остатка, что невозможно.
Значит, наше допущение неверно, а верно то, что требовалось доказать, то есть ![]() .
.
Теорема 3:
При ![]()
1)
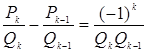 (
(![]() )
)
2)
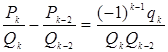 (
(![]() )
)
Доказательство: Первое соотношение можно
получить из равенства ![]() , доказанного выше, путем
деления обеих частей на
, доказанного выше, путем
деления обеих частей на ![]() .
Получаем
.
Получаем 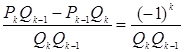
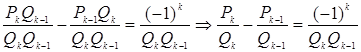 , что
и требовалось доказать.
, что
и требовалось доказать.
Докажем второе соотношение.
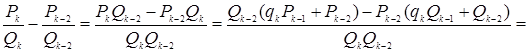
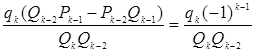 .
.
Теорема 4.
Знаменатели подходящих дробей – это натуральные числа и они образуют неубывающую последовательность, которая со второго члена становится строго возрастающей [20, c.67].
Доказательство: ![]() ,
, ![]() , так что
, так что ![]() и
и ![]() положительны.
положительны.
Соотношение ![]() (
(![]() ) (*) показывает, что и все
следующие знаменатели
) (*) показывает, что и все
следующие знаменатели ![]() положительны.
При
положительны.
При ![]() , поскольку тогда
, поскольку тогда ![]() , из (*) получаем
, из (*) получаем
![]() , что
и требовалось доказать.
, что
и требовалось доказать.
Теорема 5.
Подходящие дроби четного порядка образуют возрастающую последовательность, а нечетного порядка – убывающую последовательность [15, c.400].
Доказательство: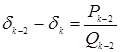 -
-![]() =
=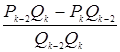 =
=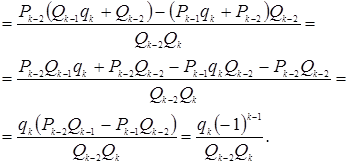
Теорема 6:
Каждая подходящая дробь четного порядка меньше соседних подходящих дробей [6, c. 211].
Доказательство: Рассмотрим дроби ![]() - подходящая дробь четного порядка.
- подходящая дробь четного порядка.
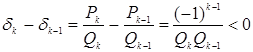 .
.
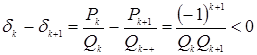
Теорема 7:
Расстояние между двумя соседними подходящими дробями 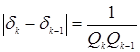 [2, c.13].
[2, c.13].
Доказательство: Так как
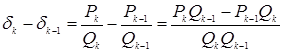 , то
, то 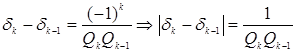 ,
,
что и требовалось доказать.
Процесс выделения целой части и перевертывания дробной можно применить к любому действительному числу.
Для иррационального числа ![]() данный
процесс должен быть бесконечным, так как конечная цепная дробь равна
рациональному числу [11, c.18].
данный
процесс должен быть бесконечным, так как конечная цепная дробь равна
рациональному числу [11, c.18].
Выражение 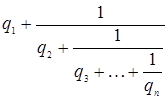 (где
(где ![]() ,
, ![]() ) (2)
) (2)
возникающее в таком процессе или заданное формально,
будем называть правильной бесконечной цепной, или непрерывной дробью, или дробью
бесконечной длины и обозначать кратко через (![]() ), а числа
), а числа ![]() – ее элементами или неполными
частными [7, c.155].
– ее элементами или неполными
частными [7, c.155].
Разложение ![]() возможно
только в единственном виде, так как процесс выделения целой части – процесс
однозначный.
возможно
только в единственном виде, так как процесс выделения целой части – процесс
однозначный.
Рассмотрим пример разложения иррационального числа ![]() .
.
Пусть ![]() .
Выделим из
.
Выделим из ![]() его целую часть.
его целую часть. ![]() =3, а дробную часть
=3, а дробную часть ![]() –3, которая меньше 1, представим в
виде
–3, которая меньше 1, представим в
виде ![]() , где
, где ![]() .
.
Повторяя операцию выделения целой части и перевертывания дробной, мы получаем:
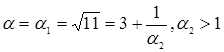 ;
;
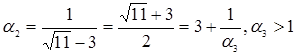 ;
;
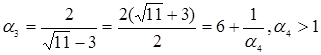 .
.
Если остановиться на этом шаге, то можно записать:
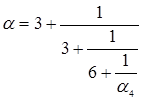 .
.
С другой стороны, из формулы для ![]() видно, что
видно, что ![]() =3+
=3+![]() . Поэтому
. Поэтому ![]() , вследствие чего, начиная с этого
момента, неполные частные станут повторяться [9, c.175].
, вследствие чего, начиная с этого
момента, неполные частные станут повторяться [9, c.175].
Бесконечная непрерывная дробь, в которой определенная последовательность неполных частных, начиная с некоторого места, периодически повторяется, называется периодической непрерывной дробью.
Если, в частности, периодическое повторение начинается с первого звена, то цепная дробь называется чисто периодической, в противном случае – смешанной периодической [6, c.70].
Чисто периодическая дробь ![]() записывается в виде
записывается в виде ![]() , а смешанная периодическая
, а смешанная периодическая ![]() в виде
в виде ![]() .
.
Итак, ![]() разлагается в смешанную
периодическую дробь (3, 3, 6, 3, 6, …) или (3, (3, 6)) [12, c.79].
разлагается в смешанную
периодическую дробь (3, 3, 6, 3, 6, …) или (3, (3, 6)) [12, c.79].
В общем случае разложения действительного
иррационального числа ![]() поступаем так же, как в
примере. Останавливаясь при этом в процессе выделения целой части после k–го
шага, будем иметь:
поступаем так же, как в
примере. Останавливаясь при этом в процессе выделения целой части после k–го
шага, будем иметь:
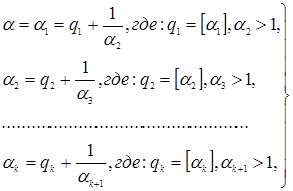 (3)
(3)
так что
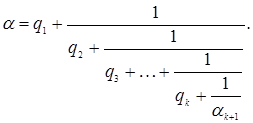
Числа ![]() называют остаточными
числами порядка k разложения
называют остаточными
числами порядка k разложения ![]() .
.
Бесконечную последовательность конечных непрерывных дробей можно построить для бесконечной цепной дроби (2).
![]()
Именно такие дроби называются подходящими. Для них останутся те же свойства, которые выводятся из закона образования знаменателей и числителей подходящих дробей, так как правило образования соответствующих им простых дробей такое же, как и для подходящих дробей в случае непрерывных конечных дробей [8, c.60].
Получаем в частности следующее:
1)
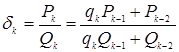 , причем
, причем 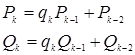 ;
;
2)
![]() , отсюда следует несократимость
подходящих дробей
, отсюда следует несократимость
подходящих дробей 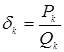 ;
;
3)
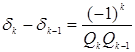 .
.
Теперь сравним подходящую дробь ![]() и кусок разложения
и кусок разложения ![]() до остаточного числа
до остаточного числа ![]() . Имеем следующее:
. Имеем следующее:
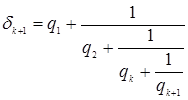
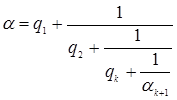 .
.
Отсюда видно, что вычисление ![]() по
по ![]() производится тем же самым
образом, что и вычисление
производится тем же самым
образом, что и вычисление ![]() по
по ![]() ,
но лишь с тем отличием, что в одном случае
,
но лишь с тем отличием, что в одном случае ![]() заменяется на
заменяется на 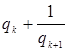 , а в другом
, а в другом ![]() заменяется на
заменяется на 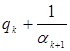 . Именно поэтому на основании следующей
формулы:
. Именно поэтому на основании следующей
формулы: 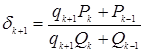 можно
сделать вывод о справедливости следующего соотношения:
можно
сделать вывод о справедливости следующего соотношения:
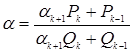 .
(5)
.
(5)
С помощью формулы (5) можно вывести теорему о расположении
подходящих дробей разложения ![]() [10, c.
370].
[10, c.
370].
Теорема. Действительное число ![]() всегда находится между двумя
соседними подходящими дробями своего разложения, причем оно ближе к
последующей, чем к предыдущей подходящей дроби [11, c.80].
всегда находится между двумя
соседними подходящими дробями своего разложения, причем оно ближе к
последующей, чем к предыдущей подходящей дроби [11, c.80].
Доказательство: Из формулы (5) следует:
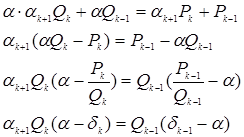
Однако ![]() ,
,
![]() , так что
, так что ![]()
1)
(![]() ) и (
) и (![]() )
имеют одинаковый знак, что означает, что
)
имеют одинаковый знак, что означает, что ![]() находится между
находится между ![]() и
и ![]() ;
;
2)
![]() , то есть
, то есть ![]() ближе к
ближе к ![]() , чем к
, чем к ![]() .
.
Так как ![]() , то
, то ![]() , и т.д.; Теперь можно сделать
следующие выводы о взаимном расположении подходящих дробей:
, и т.д.; Теперь можно сделать
следующие выводы о взаимном расположении подходящих дробей:
1)
![]() больше
всех подходящих дробей нечетного порядка и меньше всех подходящих дробей
четного порядка;
больше
всех подходящих дробей нечетного порядка и меньше всех подходящих дробей
четного порядка;
2)
подходящие
дроби нечетного порядка образуют возрастающую последовательность, а четного
порядка – убывающую. В случае, если ![]() иррационально, то
указанные последовательности являются бесконечными. В случае же рационального
иррационально, то
указанные последовательности являются бесконечными. В случае же рационального ![]() :
:
![]() .
.
————![]() ——
——![]() ————
————![]() ——
——![]() ———
———![]() ————
————
![]()
![]()
![]()
![]()
![]()
Обращая внимание на то, что при ![]() и
и ![]() , вследствие чего
, вследствие чего 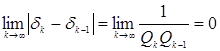 , можно сделать вывод, что в случае
иррационального
, можно сделать вывод, что в случае
иррационального ![]() сегменты
сегменты
![]() ,
, ![]() ,
… образуют стягивающуюся последовательность, которая должна иметь единственную
общую точку, которая в свою очередь, является общим пределом
последовательностей. Однако, так как
,
… образуют стягивающуюся последовательность, которая должна иметь единственную
общую точку, которая в свою очередь, является общим пределом
последовательностей. Однако, так как ![]() принадлежит всем
сегментам последовательности, то
принадлежит всем
сегментам последовательности, то ![]() совпадает с указанной
точкой, таким образом
совпадает с указанной
точкой, таким образом ![]() .
.
Следовательно, бесконечная последовательность
подходящих дробей ![]() , возникающая
при разложении иррационального
, возникающая
при разложении иррационального ![]() , сходится к
, сходится к ![]() , колеблясь около него [11,
c.81].
, колеблясь около него [11,
c.81].
Докажем, что сходится последовательность подходящих
дробей не только такой бесконечной непрерывной дроби, которая возникает при
разложении иррационального числа ![]() , но и любой бесконечной
непрерывной дроби
, но и любой бесконечной
непрерывной дроби ![]() , где
, где ![]() , а
, а ![]() -
это произвольно выбранные целые положительные числа [3, c.15].
-
это произвольно выбранные целые положительные числа [3, c.15].
Для этого необходимо заново исследовать взаимное расположение подходящих дробей.
С данной целью рассмотрим следующие формулы:
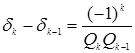 (1)
и
(1)
и 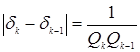 (2),
(2),
которые являются справедливыми для любой непрерывной бесконечной дроби.
1.
Любая
подходящая дробь четного порядка больше двух соседних подходящих дробей, у
которых порядок на единицу меньше или больше, чем у нее. Данное утверждение
показывает формула (1). То есть ![]() и
и ![]() . Согласно этому
. Согласно этому ![]() и
и ![]() расположены
слева от
расположены
слева от ![]() ,
, ![]() и
и ![]() –
слева от
–
слева от ![]() и так далее.
и так далее.
2. Расстояние между соседними подходящими дробями при увеличении k убывает. Данное утверждение показывает формула (2).
Действительно, так как ![]() , то
, то
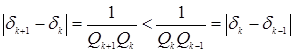
3.
Согласно
данному свойству ![]() ближе к
ближе к ![]() , чем
, чем ![]() ,
а так как
,
а так как ![]() и
и ![]() находятся слева от
находятся слева от ![]() , то
, то ![]() .
.
————![]() ———
———![]() ———
———![]() ———
———![]() ————
————
![]()
![]()
![]()
![]()
Отсюда следует, что подходящая дробь ![]() , которая, так же как и
, которая, так же как и ![]() , расположена справа от
, расположена справа от ![]() , ближе к
, ближе к ![]() , чем к
, чем к ![]() ,
то есть
,
то есть ![]() .
.
Таким же образом располагаются и подходящие дроби дальнейших порядков.
Таким образом, подходящие дроби четного порядка
убывают с ростом порядка, а подходящие дроби нечетного порядка наоборот увеличиваются
с ростом порядка. Однако, при этом все подходящие дроби четного порядка больше
всех подходящих дробей нечетного порядка, то есть ![]() при любых k
и l [5, c.40].
при любых k
и l [5, c.40].
Пары подходящих дробей ![]() ,
,
![]() , …, так как
, …, так как ![]() образуют стягивающуюся
последовательность отрезков, которая имеет единственную общую точку, которая, в
свою очередь, является общим пределом последовательностей
образуют стягивающуюся
последовательность отрезков, которая имеет единственную общую точку, которая, в
свою очередь, является общим пределом последовательностей ![]() ,
, ![]() ,
… и
,
… и ![]() ,
, ![]() ,
…. Обозначим этот предел за
,
…. Обозначим этот предел за ![]() . Далее имеем
. Далее имеем ![]() , при этом, очевидно, что
, при этом, очевидно, что ![]() для любого k,
то есть
для любого k,
то есть ![]() находится
между любыми двумя соседними подходящими дробями [8, c.
29].
находится
между любыми двумя соседними подходящими дробями [8, c.
29].
Таким образом, подходящие дроби любой непрерывной
бесконечной дроби имеют некоторый предел ![]() , который принимается в
качестве значения бесконечной непрерывной дроби. Говорят, что бесконечная
непрерывная дробь сходится к
, который принимается в
качестве значения бесконечной непрерывной дроби. Говорят, что бесконечная
непрерывная дробь сходится к ![]() или представляет число
или представляет число ![]() . Можно записать
. Можно записать ![]() , подразумевая при этом, что
, подразумевая при этом, что ![]() =
=![]() .
.
Пример 1. Представить дробь ![]() в виде цепной дроби и найти все
подходящие дроби.
в виде цепной дроби и найти все
подходящие дроби.
Решение: Для того, чтобы представить указанную дробь в виде цепной дроби рассмотрим алгоритм Евклида и разделим a на b.
![]() , остаток
, остаток ![]() ;
;
![]()
![]() ;
;
![]()
![]()
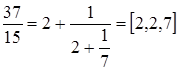 .
.
Для того, чтобы найти все
подходящие дроби воспользуемся следующим способом: пусть ![]() - первые коэффициенты цепной дроби.
Тогда
- первые коэффициенты цепной дроби.
Тогда 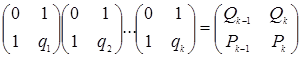 . Т.е., перемножив данные
матрицы, получаем в перевернутом виде подходящие дроби
. Т.е., перемножив данные
матрицы, получаем в перевернутом виде подходящие дроби ![]() и
и ![]() .
.
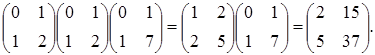
![]()
Пример 2: Разложите число ![]() в цепную дробь, замените его
подходящей дробью
в цепную дробь, замените его
подходящей дробью ![]() и укажите
погрешность замены.
и укажите
погрешность замены.
Решение: Так как 29<37 положим ![]() , а дробь
, а дробь ![]() представим в виде цепной дроби.
представим в виде цепной дроби.
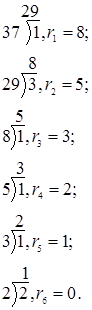
Таким образом 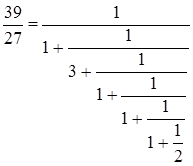 .
.
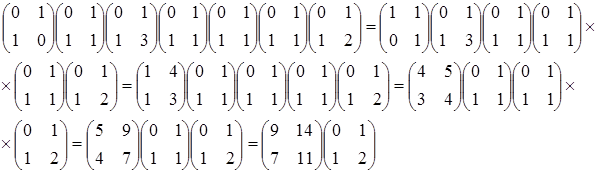
Таким образом, мы получили ![]()
Погрешность замены: ![]()
Ответ: ![]() ; погрешность:
; погрешность: ![]()
Пример 3: По данной конечной цепной дроби ![]() найдите соответствующие ей
обыкновенные несократимые дроби.
найдите соответствующие ей
обыкновенные несократимые дроби.
Решение:
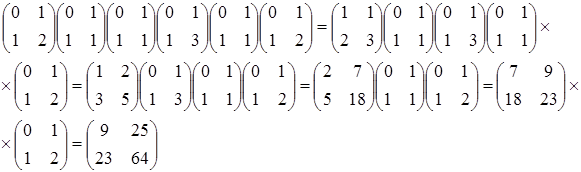
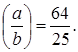
Ответ: 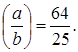
Пример 4: С помощью метода подходящих дробей решите неопределенное уравнение 119x-68y=34
Решение: ![]() =119;
=119; ![]() =68;
=68; ![]() =34.
=34.
(![]() ,
,![]() )=17. Сократим на 17 a,b и c. Получаем:
)=17. Сократим на 17 a,b и c. Получаем: ![]()
![]()
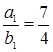
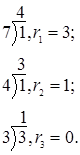
![]() ; n=2.
; n=2.



Ответ:

Таким образом, подводя итоги курсовой работы можно обобщить следующее: главным, но совсем не единственным назначением цепных дробей является то, что они позволяют находить довольно хорошие приближения вещественных чисел в виде обычных дробей. Цепные дроби широко используются в теории чисел и вычислительной математике, а их обобщения являются очень полезными в математическом анализе и многих других разделах математики. Кроме того, используются в небесной механике, физике, технике и других прикладных сферах деятельности.
Необходимо также отметить, что в данной работе удалось: определить такие понятия, как: цепные дроби, подходящие дроби, рассмотреть разложение действительного иррационального числа в правильную бесконечную цепную дробь, а так же изучить некоторые примеры с использованием цепных дробей.
Таким образом, в ходе работы были выполнены все поставленные задачи:
1. найти материал по данной теме в учебных и научных источниках;
2. определить понятие цепной дроби;
3. рассмотреть теорию правильных конечных цепных дробей и бесконечных цепных дробей;
4. проанализировать изученную литературу;
5. систематизировать и изложить материал в форме курсовой работы.
А так же была достигнута поставленная цель.
1. Алфутова Н.Б. Алгебра и теория чисел. Сборник задач для математических школ / Н.Б. Алфутова. – Москва : МЦНМО, 2002. – 264 с.
2. Арнольд В.И. Цепные дроби / В.И. Арнольд. – Москва : МЦНМО, 2015. – 40 с.
3. Бескин Н.М. Цепные дроби / Н.М. Бескин. – Москва : Квант, 1970. – 62 с.
4. Боднарчук П.И. Успехи и задачи теории цепных и ветвящихся цепных дробей / П.И. Бондарчук. – Киев : Институт математики АН УССР, 1978. – 180 с.
5. Бухштаб А.А. Теория чисел / А.А. Бухштаб. – Москва : Просвещение, 2012. – 387 с.
6. Вейль А. Основы теории чисел / А.Вейль. – Москва : Мир, 1972. – 408 с.
7. Виленкин Н.Я. Алгебра и теория чисел / Н.Я. Виленкин. – Москва : Просвящение, 2002. – 250 с.
8. Виноградов И.М. Основы теории чисел / И.М. Виноградов. – Москва : Юрайт, 2018. – 100 с.
9. Демидович Б.П. Основы вычислительной математики / Б.П. Демидович. – Москва : Физмалит, 2007. – 660 с.
10. Джоунс У. Непрерывные дроби. Аналитическая теория и приложения / У. Джоунс. – Москва : Мир, 1985. – 416 с.
11. Дэвенлорт Г. Высшая арифметика. Введение в теорию чисел / Г. Дэвенлорт. – Москва : Наука, 1965. – 176 с.
12. Кудреватов Г.А. Сборник задач по теории чисел / Г.А. Кудреватов. – Москва : Просвящение, 1970. – 200 с.
13. Ляпин Е.С. Алгебра и теория чисел / Е.С. Ляпин. – Москва : Просвящение, 2007. – 296 с.
14. Михелович Ш.Х. Теория чисел / Ш.Х. Михелович. – Москва : Высшая школ, – 1962.
15. Нестеренко Ю.В. Теория чисел / Ю.В. Нестеренко. – Москва : Просвещение, – 2008. – 438 с.
16. Ожигова Е.П. Что такое теория чисел / Е.П. Ожигова. – Москва : Знание, 1970. – 321 с.
17. Оре О. Приглашение в теорию чисел / О.Оре. – Москва : Едиториал, 2003. – 128 с.
18. Просветов Г.Н. Теория чисел: задачи и решение / Г.Н. Просветов. – Москва : Альфа-Пресс, 2010. – 72 с.
19. Хичин А.Я. Цепные дроби / А.Я. Хичин. – Москва : ГИФМЛ, 2018. – 112 с.
20. Хованский А.Н. Приложение цепных дробей и их обобщений к вопросам приближённого анализа / А.Н. Хованский. – Москва : Государственное издательство технико-теоретической литературы, 1956. – 204 с.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.