
Квадрат теңдеуді циркуль және сызғыш көмегімен шешу
Шамшиева Рахима Нажибудиговна
№24 лицей мұгалімі. Іле ауданы.Өтеген батыр кенті
ах2+вх+с=0 квадраттық
теңдеуін циркуль және сызғыш көмегімен шешу
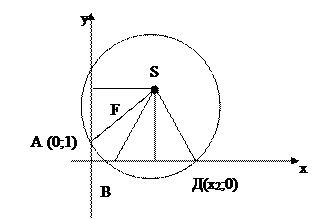
әдісін ұсынамыз (1-сурет). Ізделінді шеңбер абцисса
өсінде В(х![]() ;0) және Д (х2;0)
нүктелерінде қиылыссын делік. Мұндағы х1, х2
- ах2 + вх + с=0 теңдеуінің түбірлері
және ординат осінен А(0;1) және С(0;
;0) және Д (х2;0)
нүктелерінде қиылыссын делік. Мұндағы х1, х2
- ах2 + вх + с=0 теңдеуінің түбірлері
және ординат осінен А(0;1) және С(0;![]() )
нүктелері арқылы өтеді делік. Олай болса, қима туралы
теорема бойынша мынаны аламыз:
)
нүктелері арқылы өтеді делік. Олай болса, қима туралы
теорема бойынша мынаны аламыз:
![]()
ОВ·ОД=ОА·ОС,
бұдан ОС=![]()
1-сурет
Шеңбер центрі АС және ВД хорда ортасында орналасқан перпендикуляр SF пен SК-ның
қиылысу нүктелері болып табылады,
сондықтан![]() SК=
SК=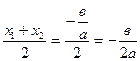 ;
;
SF =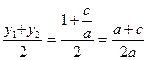
Сонымен,
1) S![]() (шеңбер
центрі) және А (0;1) нүктелерін тұрғызамыз;
(шеңбер
центрі) және А (0;1) нүктелерін тұрғызамыз;
2) SА радиусты шеңбер жүргіземіз;
3) Осы шеңбердің Ох осі арқылы өтетін қиылысу нүктелері бастапқы квадрат теңдеудің түбірі болады.
Сонымен үш түрлі жағдай болуы мүмкін:
1-ші жағдай.Шеңбер радиусы ордината
центрінен артық (АS > SК, немесе, ![]()
![]() шеңбер Ох осін екі
нүктеде (2а-сурет) В (х
шеңбер Ох осін екі
нүктеде (2а-сурет) В (х![]() ; 0) және Д
(х2;0) нүктелерде қияды. Мұндағы х1
және х2-ах2+вх+с =0 квадрат теңдеуінің
түбірлері).
; 0) және Д
(х2;0) нүктелерде қияды. Мұндағы х1
және х2-ах2+вх+с =0 квадрат теңдеуінің
түбірлері).
2-ші жағдай.Шеңбер радиусы ордината
центрінде (АS= SК; немесе ![]() тең,
шеңбер Ох осін В (х1; 0) нүктесінде (2б)-сурет) жанап
өтеді, мұндағы х1 – квадрат теңдеудің
түбірі).
тең,
шеңбер Ох осін В (х1; 0) нүктесінде (2б)-сурет) жанап
өтеді, мұндағы х1 – квадрат теңдеудің
түбірі).
3-ші жағдай.Шеңбер радиусы ордината
центрінен кіші (А S < SК, немесе ![]() ) кем,
щеңбердің абцисса осімен қиылысатын нүктесі жоқ
(2в – сурет), бұл жағдайда теңдеудің шешімі болмайды.
) кем,
щеңбердің абцисса осімен қиылысатын нүктесі жоқ
(2в – сурет), бұл жағдайда теңдеудің шешімі болмайды.
![]()
![]()
![]() у у
у
у у
у
 |
|||||
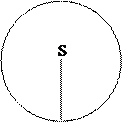 |
|||||
 |
|||||
А(0;1) В 0 х2 х х х А(0;1) 0 В А 0 х1 В
![]()
![]()
![]()
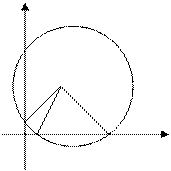
2-сурет
а) АS>SВ, ![]() екі шешімі
бар: х1 және х2
екі шешімі
бар: х1 және х2
б) АS=SВ, ![]() бір шешімі
бар: х1
бір шешімі
бар: х1
в) АS<SВ, ![]() шешім
жоқ.
шешім
жоқ.
Қолданылған әдебиеттер:
1. Математика, информатика, физика журналы . №5, 2003ж.
2. Брадис В.М. Төрт таңбалы матем. таблицалар – М.: Просвещение, 1990
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.