
Дагестанский Государственный Университет
факультет физики,
кафедра теоретической физики,
магистратура, 1 курс.
Курсовая работа
на тему
«Туннельный эффект в сверхпроводниках»
Выполнила
Аскадинова Заира Магомедсаидовна.
Руководитель:
Мусаев Гапиз Мусаевич.
Махачкала. 2013.
Ощущение тайны – наиболее
прекрасное из доступных нам переживаний.
Именно это чувство стоит у колыбели
истинного искусства и настоящей науки.
Альберт Энштейн.
Аннотация
Объектом исследования данной работы является математический аппарат описания эффекта Джозефсона. В экспериментальной части описаны вольт-амперные характеристики туннельного диода. В теоретической части – стационарный и нестационарный эффекты Джозефсона в туннельном SIS-контакте, в простейшем сквиде, в SIN-контакте, в SINIS-контакте, эффект резонанса, применение сверхпроводников Также рассмотрена теория Асламазова и Ларкина, теория Гинзбурга–Ландау.
Объем работы составляет 47 стр. Курсовая работа содержит следующие части: теория, эксперимент, результаты, выводы.
Содержание
Введение.............................................................................................................................4
Глава 1. Туннельные эффекты.........................................................................................5
Глава 2. Джозефсоновский ток...................................................................................7
§1. Теория Гинзбурга–Ландау........................................................................................7
§2. Общие свойства джозефсоновского тока..............................................................11
Глава 3. Стационарный эффект Джозефсона.............................................................13
§1. Эффект Джозефсона в туннельном SIS-контакте.................................................13
§2. Простейший сквид................................................................................................14
§3. Эффект близости в SIN-контакте..........................................................................15
§4. Эффект Джозефсона в SINIS-контакте...................................................................16
§5. Теория Асламазова и Ларкина.............................................................................18
Глава 4. Нестационарный эффект Джозефсона в туннельных структурах................21
§1. Общие свойства....................................................................................................21
§2. Резистивная модель..............................................................................................24
§3. Резистивная модель с ёмкостью...........................................................................28
Глава 5.Использование сверхпроводимости..............................................................30
§1. Контактом Джозефсона........................................................................................33
§2. Сканирующая туннельная микроскопия...............................................................35
Эксперимент..............................................................................................................36
§1. Элементы теории туннельного эффекта...............................................................36
§2. Туннельный диод.................................................................................................41
Заключение................................................................................................................46
Литература............................................................................................................................47
Введение
Термин эффект Джозефсона в настоящее время относится к совокупности явлений, имеющих место в контактах двух сверхпроводников через слабую связь. В 1962 году появилась короткая теоретическая работа английского физика Б.Д. Джозефсона, где исследовался туннельный переход (контакт сверхпроводников через прослойку диэлектрика), и было предсказано два эффекта:
1) через контакт в отсутствие приложенного напряжения может течь постоянный сверхпроводящий ток;
2) при конечном напряжении ![]() через контакт помимо обычного
постоянного тока будет также течь переменный сверхпроводящий ток частоты
через контакт помимо обычного
постоянного тока будет также течь переменный сверхпроводящий ток частоты![]() .
.
Это предсказание было весьма необычным и вызвало серьёзные споры, в которых некоторые учёные, в том числе весьма именитые, ставили предсказанные эффекты под сомнение. Независимые вычисления других теоретиков, однако, показали правильность результатов Джозефсона, а затем они были подтверждены и экспериментом.
В 1973 году Джозефсон получил за своё открытие Нобелевскую премию.
Дальнейшие исследования показали, что эффект Джозефсона весьма общий и проявляется не только в туннельных переходах, но и при соединении двух сверхпроводников через слабую связь любого вида (например, нормальный металл, ферромагнетик, геометрическое сужение и др.).
Одной из мотиваций, приведших Джозефсона к открытию,
являлось желание выяснить, имеет ли какие-либо наблюдаемые следствия фаза
параметра порядка. Действительно, как известно, сверхпроводник описывается
комплексным параметром порядка ![]() . Модуль параметра
порядка
. Модуль параметра
порядка![]() определяет как
бы «силу» сверхпроводимости, в частности сверхпроводящую щель в одночастичном
спектре. А фаза
определяет как
бы «силу» сверхпроводимости, в частности сверхпроводящую щель в одночастичном
спектре. А фаза ![]() ? На что она влияет? Что
будет, например, если привести в контакт два сверхпроводника с одинаковыми по
модулю, но разными по фазе параметрами порядка? Именно из этих вопросов и
возникла работа Джозефсона. Оказалось, что величина сверхпроводящего тока через
контакт (джозефсоновского тока) определяется именно разностью фаз параметров
порядка с двух сторон. Параметр порядка
? На что она влияет? Что
будет, например, если привести в контакт два сверхпроводника с одинаковыми по
модулю, но разными по фазе параметрами порядка? Именно из этих вопросов и
возникла работа Джозефсона. Оказалось, что величина сверхпроводящего тока через
контакт (джозефсоновского тока) определяется именно разностью фаз параметров
порядка с двух сторон. Параметр порядка ![]() можно рассматривать как волновую функцию
сверхпроводящего конденсата (куперовских пар электронов), поэтому эффект
Джозефсона — квантовый эффект. С другой стороны, конденсат куперовских пар
состоит из огромного количества электронов, и в джозефсоновском токе участвует огромное
число электронов, поэтому эффект Джозефсона — одновременно и макроскопический
эффект. Он явился очень важным шагом в понимании природы сверхпроводящего
состояния. Кроме того, он нашёл значительное и растущее число применений для
создания уникальных измерительных приборов. Ниже я пытаюсь на основе простых
примеров объяснить физику эффекта Джозефсона и основные явления, связанные с ним.
можно рассматривать как волновую функцию
сверхпроводящего конденсата (куперовских пар электронов), поэтому эффект
Джозефсона — квантовый эффект. С другой стороны, конденсат куперовских пар
состоит из огромного количества электронов, и в джозефсоновском токе участвует огромное
число электронов, поэтому эффект Джозефсона — одновременно и макроскопический
эффект. Он явился очень важным шагом в понимании природы сверхпроводящего
состояния. Кроме того, он нашёл значительное и растущее число применений для
создания уникальных измерительных приборов. Ниже я пытаюсь на основе простых
примеров объяснить физику эффекта Джозефсона и основные явления, связанные с ним.
Глава 1. Туннельные эффекты.
Туннельный эффект известен в физики давно. Это один из основных квантово- механических эффектов и разобраться в нем можно только подходя с помощи квантового описания происходящих событий.
Представьте себе горизонтальный желоб, по которому без трения скользит массивный шарик. Что произойдет, если шарик встретит на своем пути горку – участок с наклоном? По оси абсцисс отложена координата шарика х, а по оси ординат – его потенциальная энергия.
Теряя скорость, шарик покатиться в гору. Если его начальная кинетическая энергия была больше потенциальной максимальной энергии, то она благополучно перевалить через вершину горки шарик не сможет. На склоне найдется такая «точка поворота», где вся кинетическая энергия перейдет в потенциальную, и в соответствии с законом сохранения энергии шарик остановиться, а затем покатиться обратно. Шансов проникнуть за барьер (горку) у него абсолютно никаких.
А вот квантовая частица – электрон, на пути которого возникает преграда, в аналогичной ситуации все же как-то «умудряется» просочиться через барьер.
Попытаемся внести в этот абстрактный образ до некоторой степени противоречащий нашему здравому смыслу ввести хотя бы некоторый элемент наглядности. Невозможность проникновения частицы (в нашем случае шарика) в область за барьером можно уподобить известному в оптике явлению полного внутреннего отражения. Согласно геометрической оптике лучи, подающие под углом больше предельного не проникают, не проникают из среда оптически более плотной, в среду, оптически менее плотную.
Однако более подробное рассмотрение этого явления, основанное на законах не геометрической, а волновой оптике, приводит к возможности проникновения света во вторую среду. При этом если оптически более плотная среда представляет собой тонкую пластину, то световая волна проходит сквозь неё, несмотря на то, что угол падения больше предельного.
А теперь вспомним о двойственной природе электрона. Частица в квантовой механике – это не совсем обычный шарик, пусть даже сверхмалых размеров, она даже обладает и волновыми свойствами, а волна, как мы выяснили, все же слегка проникает в запретную область, она как бы проверяет возможность проникновения в эту среду. При этом амплитуда затухает и тем быстрее, или говорят иначе, чем выше энергетический барьер. Выходит, что какова бы не была энергия электрона и как бы ни был высок энергетический барьер, всегда есть отличная от нуля вероятность найти электрон внутри барьера, а если барьер не очень гладок, то и за барьером, по другую сторону. Тогда на обратной стороне барьера появляется конечная амплитуда, а согласно законам квантовой механики квадрат амплитуды и определяет вероятность того, что электрон будет здесь найден, если провести соответствующие эксперименты. При этом электроны «пробивают» только строго горизонтальные туннели, на выходе из которых полная энергия частиц точно такая же, как и на входе. Тунелирование возможно только в том случае, если уровни, на которые переходят электроны, не заняты, и то в противном случае запрет Паули.
Итак, не имея достаточной энергии, чтобы перескочить через преграду, как бы «порывает» туннель в его недрах. Вероятность такого перехода, или как говорят физики, прозрачность энергии зависит от энергии электрона и очень сильно от ширины и высоты барьера. Туннельный эффект становиться наблюдаем лишь при очень малых толщинах барьеров, так что у применяемых электрических изоляционных покрытий громадный запас прочности в отношении туннельного тока.
Итак, Эффект Джозефсона — явление протекания сверхпроводящего тока через тонкий слой диэлектрика, разделяющий два сверхпроводника. Такой ток называют джозефсоновским током, а такое соединение сверхпроводников — джозефсоновским контактом. В первоначальной работе Джозефсона предполагалось, что толщина диэлектрического слоя много меньше длины сверхпроводящей когерентности, но последующие исследования показали, что эффект сохраняется и на гораздо больших толщинах.
Глава 2. Джозефсоновский ток.
§1. Теория Гинзбурга–Ландау.
Существенная часть
этого рассмотрения будет построена на описании сверхпроводимости в рамках теории
Гинзбурга–Ландау. Полная
теория, описывающая поведение сверхпроводника, довольно сложна. Ситуация, однако,
существенно упрощается в области температур вблизи точки сверхпроводящего
перехода![]() . Здесь
оказывается возможным построить систему относительно простых уравнений. В общей
теории Ландау фазовых переходов второго рода отличие «несимметричной» фазы от «симметричной»
описывается параметром порядка, обращающимся в точке перехода в нуль. Для сверхпроводящей
фазы естественным таким параметром является конденсатная волновая функция(её ещё
иногда называют волновой функцией куперовских пар). Отправным пунктом теории Гинзбурга–Ландау
(ГЛ) является выражение для свободной энергии сверхпроводника как функционала от
параметра порядка. В соответствии с общими положениями теории Ландау, оно получается
разложением плотности свободной энергии по степеням малого (вблизи точки перехода)
параметра порядка и его производных по координатам. Во избежание излишних (с принципиальной
точки зрения) усложнений будем считать, что сверхпроводящее состояние - спин-синглетное
(полный спин куперовской пары
. Здесь
оказывается возможным построить систему относительно простых уравнений. В общей
теории Ландау фазовых переходов второго рода отличие «несимметричной» фазы от «симметричной»
описывается параметром порядка, обращающимся в точке перехода в нуль. Для сверхпроводящей
фазы естественным таким параметром является конденсатная волновая функция(её ещё
иногда называют волновой функцией куперовских пар). Отправным пунктом теории Гинзбурга–Ландау
(ГЛ) является выражение для свободной энергии сверхпроводника как функционала от
параметра порядка. В соответствии с общими положениями теории Ландау, оно получается
разложением плотности свободной энергии по степеням малого (вблизи точки перехода)
параметра порядка и его производных по координатам. Во избежание излишних (с принципиальной
точки зрения) усложнений будем считать, что сверхпроводящее состояние - спин-синглетное
(полный спин куперовской пары ![]() ) и s-волновое
(полный орбитальный момент куперовской пары
) и s-волновое
(полный орбитальный момент куперовской пары ![]() ,т.е.
состояние изотропное). Параметр порядка в этом случае сводится к комплексному скаляру.
Тогда разложение свободной энергии для сверхпроводника в магнитном поле имеет вид:
,т.е.
состояние изотропное). Параметр порядка в этом случае сводится к комплексному скаляру.
Тогда разложение свободной энергии для сверхпроводника в магнитном поле имеет вид:
 , (1), где
, (1), где
![]() — свободная энергия в нормальном состоянии
в отсутствие магнитного поля,
— свободная энергия в нормальном состоянии
в отсутствие магнитного поля,
∆ — параметр порядка,
![]() — заряд электрона,
— заряд электрона,
![]() — векторный потенциал внешнего магнитного
поля B,
— векторный потенциал внешнего магнитного
поля B,
![]() — критическая температура сверхпроводника,
записанная в энергетических единицах, поэтому константа Больцмана нигде в
формулах не возникает.
— критическая температура сверхпроводника,
записанная в энергетических единицах, поэтому константа Больцмана нигде в
формулах не возникает.
Коэффициент 2 перед векторным потенциалом — это есть прямое следствие того, что в сверхпроводимости участвуют пары электронов. Интегрирование ведётся по объёму образца.
Теперь обсудим коэффициенты в
разложении свободной энергии (1). Величина ![]() имеет
размерность времени, изменяет знак в точке сверхпроводящего перехода,
так что
имеет
размерность времени, изменяет знак в точке сверхпроводящего перехода,
так что ![]() (2), где
(2), где
![]() — температура.
— температура.
Удобно нормировать параметр порядка так, чтобы его модуль совпадал
с щелью в квазичастичной плотности состояний объёмного образца. Коэффициенты ![]() ,
,![]() ,
,![]() и
и ![]() слабо
зависят от температуры, и их можно найти из модели сверхпроводимости Бардина–Купера–Шриффера
(БКШ). Мне будет в основном интересен так называемый грязный предел (реализующийся,
например, в сверхпроводящих сплавах с примесями), когда длина свободного пробега
электрона
слабо
зависят от температуры, и их можно найти из модели сверхпроводимости Бардина–Купера–Шриффера
(БКШ). Мне будет в основном интересен так называемый грязный предел (реализующийся,
например, в сверхпроводящих сплавах с примесями), когда длина свободного пробега
электрона ![]() много меньше, чем
много меньше, чем ![]() (характерный размер куперовской пары
при
(характерный размер куперовской пары
при ![]() ), — именно такая ситуация чаще всего
реализуется в эксперименте. В этом случае
), — именно такая ситуация чаще всего
реализуется в эксперименте. В этом случае ![]() совпадает
с коэффициентом диффузии электрона на уровне Ферми (т.е.
совпадает
с коэффициентом диффузии электрона на уровне Ферми (т.е.![]() ,
где
,
где ![]() — скорость Ферми), а остальные коэффициенты
имеют следующие значения:
— скорость Ферми), а остальные коэффициенты
имеют следующие значения:
![]() ,
, ![]() ,
, ![]() ,
(3), где
,
(3), где
![]() — плотность состояний электрона на уровне
Ферми в нормальном состоянии,
— плотность состояний электрона на уровне
Ферми в нормальном состоянии,
![]() — импульс Ферми,
— импульс Ферми,
![]() ;
;![]() -
дзета-функция Римана.
-
дзета-функция Римана.
В то же время чистый случай отличается лишь значениями коэффициентов в выражении (1) для свободной энергии:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
где
,
где
![]() — плотность электронов,
— плотность электронов,
![]() — энергия Ферми,
— энергия Ферми,
![]() — масса электрона.
— масса электрона.
Условие применимости разложения (1) — малость
параметра порядка ![]() по сравнению с его значением
по сравнению с его значением
![]() при T≪ T. Для сверхпроводника
при T≪ T. Для сверхпроводника![]() ~
~![]() и
и
![]() ~
~![]() ~
~![]() , откуда следует условие
, откуда следует условие![]() . Кроме того, ∆ должна меняться
в пространстве не слишком быстро, а именно на расстояниях много больших
. Кроме того, ∆ должна меняться
в пространстве не слишком быстро, а именно на расстояниях много больших ![]() . Именно это позволяет оставить в
уравнении (1) основные вклады по параметру порядка и его производным, в то время
как отброшенные члены имеют более высокий порядок малости (при этом удерживать член
четвёртого порядка по ∆ рядом с квадратичным необходимо, т.к. коэффициент
при квадратичном члене очень мал; вклады нечётного порядка по ∆ отсутствуют,
т.к. параметр порядка определён с точностью до общего фазового множителя, в
результате чего энергия не должна меняться при изменении знака ∆).
. Именно это позволяет оставить в
уравнении (1) основные вклады по параметру порядка и его производным, в то время
как отброшенные члены имеют более высокий порядок малости (при этом удерживать член
четвёртого порядка по ∆ рядом с квадратичным необходимо, т.к. коэффициент
при квадратичном члене очень мал; вклады нечётного порядка по ∆ отсутствуют,
т.к. параметр порядка определён с точностью до общего фазового множителя, в
результате чего энергия не должна меняться при изменении знака ∆).
Из
условия минимума свободной энергии можно найти уравнения, которым удовлетворяет
параметр порядка. Приравнивая вариацию ![]() по
по
![]() и A нулю, найдём
и A нулю, найдём
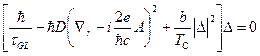 ,
(4)
,
(4)
![]() ,
(5)
,
(5)
![]() , (6)
, (6)
где ![]() — плотность сверхпроводящего тока.
— плотность сверхпроводящего тока.
Хочу обратить внимание, что если сделать замену ![]() , и
, и ![]() в
(6), то выражение для тока примет такой же вид, как ток в квантовой механике одной
частицы с волновой функцией
в
(6), то выражение для тока примет такой же вид, как ток в квантовой механике одной
частицы с волновой функцией ![]() , зарядом
, зарядом ![]() и массой
и массой ![]() .
Квадрат модуля волновой функции имеет размерность плотности вероятности, как и должно
быть в квантовой механике, и равен плотности куперовских пар (это и есть «частицы»
с зарядом
.
Квадрат модуля волновой функции имеет размерность плотности вероятности, как и должно
быть в квантовой механике, и равен плотности куперовских пар (это и есть «частицы»
с зарядом ![]() и массой
и массой ![]() ).
Плотность сверхпроводящих электронов
).
Плотность сверхпроводящих электронов ![]() по определению в
два раза больше плотности куперовских пар, поэтому
по определению в
два раза больше плотности куперовских пар, поэтому ![]() .Замечу
также, что (5) — одно из уравнений Максвелла.
.Замечу
также, что (5) — одно из уравнений Максвелла.
В однородном сверхпроводнике в отсутствие
магнитного поля градиентный член в (4) равен нулю. В этом случае находим 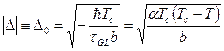 . (7)
. (7)
При наличии и градиентного члена из
самого вида уравнения (4) ясно, что возникает характерная длина 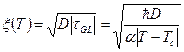 . (8)
. (8)
Эту длину можно трактовать как размер куперовской пары при температурах, близких к критической.
Очень важной особенностью формулы (6) для
тока является то, что в отсутствие векторного потенциала сверхпроводящий ток возникает
только в случае изменения в пространстве фазы параметра порядка. Например, если
модуль параметра порядка постоянен, т.е. ![]() ,
мы получаем
,
мы получаем ![]() .
(9)
.
(9)
Система
уравнений (4)–(6) станет замкнутой после того, как будут сформулированы граничные
условия для ∆. На границе, совершенно непроницаемой для электронов (граница
сверхпроводника с вакуумом или, например, толстый слой окисла), граничные условия
имеют вид ![]() ,
(10) где
,
(10) где ![]() — нормаль к поверхности.
— нормаль к поверхности.
Уравнение (10) можно вывести из условия равенства нулю интегралов по поверхности в вариации свободной энергии (1). Отсюда следует, в частности, отсутствие тока через непроницаемую границу.
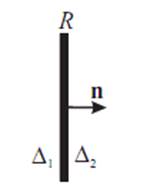 Рис.1. Граница с сопротивлением R между двумя сверхпроводниками с параметрами порядка ∆
и ∆2.
Рис.1. Граница с сопротивлением R между двумя сверхпроводниками с параметрами порядка ∆
и ∆2.
Общие граничные условия на границе между двумя
сверхпроводниками (см.рис.1) должны находиться, вообще говоря, из микроскопических
соображений, исходя из поведения параметра порядка на расстояниях ![]() вблизи границы. Однако уже на расстоянии
порядка
вблизи границы. Однако уже на расстоянии
порядка![]() вблизи границы уравнения ГЛ неприменимы,
поэтому невозможно сшить решения по разную сторону границы, опираясь только на феноменологическую
теорию ГЛ.
вблизи границы уравнения ГЛ неприменимы,
поэтому невозможно сшить решения по разную сторону границы, опираясь только на феноменологическую
теорию ГЛ.
Если предположить, что материальные параметры веществ, находящихся с двух сторон контакта (проводимость, коэффициент диффузии, плотность состоянии на уровне Ферми в нормальном состоянии), одинаковы. Константы электрон-электронного взаимодействия предполагаются близкими, но тем не менее могут отличаться, так что в некотором диапазоне температур одна из сторон может быть в сверхпроводящем состоянии, а другая — в нормальном (такие системы будут рассмотрены ниже). Кроме того, естественно, могут быть различными (произвольными) фазы параметров порядка с двух сторон. Уравнение ГЛ (4) имеет второй порядок по градиентам, как и уравнение Шрёдингера. Поэтому естественно, что на границе возни кают два граничных условия назначения параметров порядка и их производных с двух сторон:
![]() (11)
(11)
Вид правой части можно было бы угадать, исходя из требования
линейности по ![]() и
и ![]() (так как параметр порядка мал), а также
из того, что при перестановке местами полупространств 1 и 2 ток должен менять направление
— поэтому должна войти разность
(так как параметр порядка мал), а также
из того, что при перестановке местами полупространств 1 и 2 ток должен менять направление
— поэтому должна войти разность ![]() и
и ![]() .
.
Параметр![]() имеет
размерность длины и равен
имеет
размерность длины и равен ![]() ~
~![]() , где
, где
![]() — проводимость сверхпроводника в нормальном
состоянии (при нагревании выше T),
— проводимость сверхпроводника в нормальном
состоянии (при нагревании выше T),
![]() и
и ![]() —
сопротивление и площадь границы,
—
сопротивление и площадь границы,
![]() — длина свободного пробега,
— длина свободного пробега,
![]() —вероятность туннелирования электрона
с энергией порядка энергии Ферми через границу между сверхпроводниками при
—вероятность туннелирования электрона
с энергией порядка энергии Ферми через границу между сверхпроводниками при ![]() .
.
Хочу обратить внимание на следующую связь между формулой (6) для тока в объёме сверхпроводника и граничным условием (11): обе формулы показывают, что сверхпроводящий ток связан с изменением параметра порядка в пространстве (градиент в объёме и разность параметров порядка с двух сторон границы соответственно).
Используя (6), можно записать граничные условия (11) через ток на границе:
![]() (12)
(12)
Уравнение (12) — одно из самых важных для объяснения в рамках приближения ГЛ эффекта интерференции волновых функций конденсатов двух близких сверхпроводников (эффект Джозефсона).
§2. Общие свойства джозефсоновского тока
Из симметрийных соображений можно определить многие свойства
джозефсоновского тока. Подобно тому, как внутри сверхпроводников ток определяется
градиентом фазы конденсатной волновой функции (см. (9)), так величина протекающего
через контакт сверхпроводящего тока ![]() связана с разностью
значений
связана с разностью
значений ![]() фаз параметра порядка в двух берегах
контакта.
фаз параметра порядка в двух берегах
контакта.
Поскольку значения фаз, отличающиеся
на целое кратное от ![]() , физически тождественны,
ясно, что ток
, физически тождественны,
ясно, что ток ![]() должен быть в общем
случае периодической функцией разности фаз с периодом
должен быть в общем
случае периодической функцией разности фаз с периодом ![]() :
:
![]() (13). Влиянием
на ток со стороны собственного магнитного поля токов внутри контакта можно пренебречь
— в противном случае вместо разности сверхпроводящих фаз должно было бы фигурировать
калибровочно инвариантное выражение, включающее в себя векторный потенциал).
(13). Влиянием
на ток со стороны собственного магнитного поля токов внутри контакта можно пренебречь
— в противном случае вместо разности сверхпроводящих фаз должно было бы фигурировать
калибровочно инвариантное выражение, включающее в себя векторный потенциал).
Операция обращения времени меняет знак тока
![]() и в то же время меняет знак фаз (поскольку
волновые функции заменяются своими комплексно-сопряжёнными). Это значит, что ток
и в то же время меняет знак фаз (поскольку
волновые функции заменяются своими комплексно-сопряжёнными). Это значит, что ток
![]() должен быть нечётной функцией разности
фаз и обращаться в нуль при разности фаз, равной нулю:
должен быть нечётной функцией разности
фаз и обращаться в нуль при разности фаз, равной нулю: ![]() ,
, ![]() (14).
(14).
Кроме того, поскольку сверхпроводящий ток
может течь лишь в присутствии градиента фазы параметра порядка, ток через слабую
связь будет отсутствовать не только при ![]() ,
но и при
,
но и при ![]() (этот случай соответствует изменению
знака за счёт прохождения параметра порядка через ноль, а не за счёт непрерывного
изменения фазы). В результате можно утверждать, что
(этот случай соответствует изменению
знака за счёт прохождения параметра порядка через ноль, а не за счёт непрерывного
изменения фазы). В результате можно утверждать, что ![]() (15).
(15).
Будучи, разумеется, ограниченной, функция![]() имеет свои максимальное и минимальное
значения, между которыми она и меняется при изменении разности фаз, а в силу нечётности
функции эти значения одинаковы по абсолютной величине; обозначу их через
имеет свои максимальное и минимальное
значения, между которыми она и меняется при изменении разности фаз, а в силу нечётности
функции эти значения одинаковы по абсолютной величине; обозначу их через ![]() :
: ![]() (16).
(16).
Эти свойства не зависят от типа слабой связи и являются общими для всех видов джозефсоновских контактов.
Глава 3. Стационарный эффект Джозефсона
§1. Эффект Джозефсона в туннельном SIS-контакте
Рассмотрим простейший (и исторически первый) тип джозефсоновского контакта — два сверхпроводника (S), разделённых тонким слоем диэлектрика (I), —такой контакт называют туннельным, или SIS- контактом. Для электронов слой диэлектрика представляет собой потенциальный барьер, и если слой достаточно тонок, то существует конечная вероятность их проникновения через него путём квантового туннелирования. Даже если коэффициент пропускания барьевого туннелирования. Даже если коэффициент пропускания барьеной конденсатной волновой функцией. Это обстоятельство и приводит к эффекту Джозефсона. Единство конденсатной волновой функции системы означает, что через контакт между двумя сверхпроводниками может течь, даже в отсутствие приложенной извне разности потенциалов, сверхпроводящий ток (например, в системе, изображённой на рис.2).
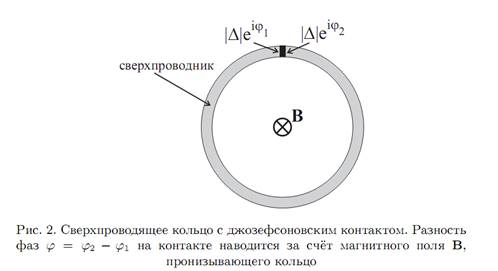
Если граница мало прозрачна, то модули
параметров порядка с двух сторон от границы совпадают со своими значениями (7) в
объёме, и параметры порядка отличаются только фазами: ![]() Используя
граничные условия (12), легко получаем, что плотность тока на границе равна
Используя
граничные условия (12), легко получаем, что плотность тока на границе равна ![]() (17).
(17).
Умножив (17) на площадь поверхности контакта![]() , получим полный ток:
, получим полный ток:
![]() ,
, ![]() (18).
(18).
С учётом (7) получаем линейную зависимость критического тока от температуры:
![]() ,
, ![]() (19).
(19).
§2. Простейший сквид
Рассмотрим сверхпроводящее кольцо, сделанное из толстого сверхпроводящего
провода, замкнутое через джозефсоновский контакт (см.рис.2). Пусть толщина провода
много больше мейсснеровской глубины проникновения магнитного поля ![]() , тогда ток внутри провода равен нулю
(т.к. магнитное поле заэкранировано поверхностными мейсснеровскими токами), и модуль
параметра порядка постоянен, в то время как фаза может зависеть от координаты. Подставляя
, тогда ток внутри провода равен нулю
(т.к. магнитное поле заэкранировано поверхностными мейсснеровскими токами), и модуль
параметра порядка постоянен, в то время как фаза может зависеть от координаты. Подставляя
![]() в формулу (6) для тока и
интегрируя от стороны контакта 1 до стороны контакта 2 по контуру
в формулу (6) для тока и
интегрируя от стороны контакта 1 до стороны контакта 2 по контуру ![]() , проходящему внутри провода, получаем
, проходящему внутри провода, получаем
![]() (20),
где
(20),
где
![]() — магнитный поток
внутри кольца.
— магнитный поток
внутри кольца.
В результате![]()
![]() (21),
(21),
где введён квант магнитного потока ![]() .
.
И
окончательно: 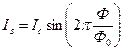 .
(22)
.
(22)
Таким образом, джозефсоновский ток весьма чувствителен к величине
магнитного поля (т.к. ![]() мало). Используя это свойство
эффекта Джозефсона, можно измерять магнитное поле с высокой точностью. Кольцо с
джозефсоновским контактом, рассмотренное выше, является простейшим примером сквида
(от английского сокращения SQUID—superconducting quantum interference device, т.е.
сверхпроводящее квантовое интерференционное устройство) — прибора, измеряющего магнитное
поле с высокой точностью.
мало). Используя это свойство
эффекта Джозефсона, можно измерять магнитное поле с высокой точностью. Кольцо с
джозефсоновским контактом, рассмотренное выше, является простейшим примером сквида
(от английского сокращения SQUID—superconducting quantum interference device, т.е.
сверхпроводящее квантовое интерференционное устройство) — прибора, измеряющего магнитное
поле с высокой точностью.

§3. Эффект близости в SIN-контакте
Рассмотрим теперь контакт сверхпроводник–диэлектрик–нормальный
металл (сокращённо SIN). Сверхпроводящий параметр порядка, вообще говоря, не равен
нулю в нормальном металле вблизи границы со сверхпроводником. Такое «индуцирование»
сверхпроводимости в нормальный металл называют эффектом близости. Количественно
эффект близости в системе, где сверхпроводник занимает полупространство ![]() , а нормальный металл — полупространство
, а нормальный металл — полупространство
![]() (см.рис.3а), может быть описан в рамках
теории Гинзбурга–Ландау. Поскольку теория ГЛ применима при температурах, близких
к критической, необходимо, чтобы нормальный металл был в действительности нормальным
состоянием сверхпроводника, имеющего более низкую критическую температуру
(см.рис.3а), может быть описан в рамках
теории Гинзбурга–Ландау. Поскольку теория ГЛ применима при температурах, близких
к критической, необходимо, чтобы нормальный металл был в действительности нормальным
состоянием сверхпроводника, имеющего более низкую критическую температуру ![]() . Тогда в интервале температур
. Тогда в интервале температур ![]() (и в случае выполнения условия система
будет представлять собой SIN-контакт, в котором применима теория ГЛ. Будем предполагать,
что магнитное поле отсутствует (A=0), тогда фазу параметра порядка в SIN-контакте
можно выбрать равной нулю, поэтому параметр порядка вещественен. Задача теперь
сводится к решению уравнения (4) с граничными условиями (11). В случае непрозрачной
границы параметр порядка слева давался бы выражением (7), а справа был бы равен
нулю. В случае же слабопрозрачной границы параметр порядка можно представить в виде
(и в случае выполнения условия система
будет представлять собой SIN-контакт, в котором применима теория ГЛ. Будем предполагать,
что магнитное поле отсутствует (A=0), тогда фазу параметра порядка в SIN-контакте
можно выбрать равной нулю, поэтому параметр порядка вещественен. Задача теперь
сводится к решению уравнения (4) с граничными условиями (11). В случае непрозрачной
границы параметр порядка слева давался бы выражением (7), а справа был бы равен
нулю. В случае же слабопрозрачной границы параметр порядка можно представить в виде
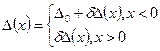 (23)
(23)
где ![]() . Линеаризуя уравнения по
. Линеаризуя уравнения по ![]() , получаем
, получаем
 ,
, ![]() (24)
(24)
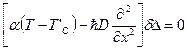 ,
,
![]() (25)
(25)
![]() ,
,
![]() . (26)
. (26)
Решая эти уравнения
получим, что  (27) , где
(27) , где
![]() и
и ![]() .
.
Схематическая зависимость параметра порядка от координаты
приведена на рис.3б. Легко увидеть, что ![]() ~
~![]() примерно равно размеру куперовской
пары в сверхпроводнике (нормальном металле). Следовательно, условие малости
примерно равно размеру куперовской
пары в сверхпроводнике (нормальном металле). Следовательно, условие малости ![]() , т.е.
, т.е. ![]() ,
означает, что куперовская пара должна быть много меньше
,
означает, что куперовская пара должна быть много меньше![]() ,что
может реализоваться при малой прозрачности границы между сверхпроводником и нормальным
металлом.
,что
может реализоваться при малой прозрачности границы между сверхпроводником и нормальным
металлом.
Когда это условие не выполняется, линеаризация уравнений ГЛ неприменима и необходимо, решать общие нелинейные уравнения.
§4. Эффект Джозефсона в SINIS-контакте
Эффект Джозефсона связан с тем, что в системе устанавливается единый параметр порядка. В туннельном контакте параметр порядка проникал через туннельный барьер. В предыдущем разделе я показала, что параметр порядка может проникать в нормальный металл. Это означает, что эффект Джозефсона возможен в системе SINIS (контакт двух сверхпроводников через нормальный металл с диэлектрическими прослойками на границах), где он весьма наглядно проявляется в виде интерференции параметров порядка, приходящих от двух берегов.
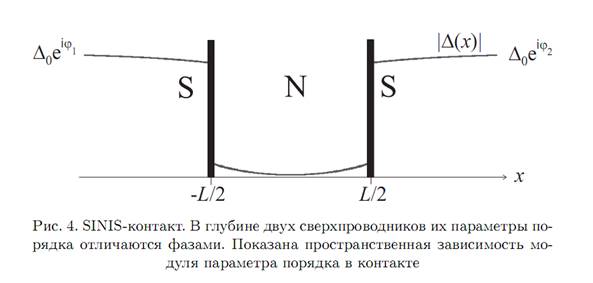
Количественно эффект Джозефсона в системе SINIS (см.рис.4) может быть описан в рамках теории ГЛ в тех же предположениях, что и в предыдущем разделе. В отличие от предыдущего раздела необходимо учесть разные фазы в глубине сверхпроводников:
![]() . Нужно найти решение в нормальной части
контакта и затем вычислить ток.
. Нужно найти решение в нормальной части
контакта и затем вычислить ток.
В граничные условия теперь добавляются фазы:
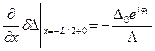 ,
,  (28)
(28)
![]()
Решение уравнения ГЛ при ![]() будем искать в виде
линейной комбинации решений, приходящих от двух берегов:
будем искать в виде
линейной комбинации решений, приходящих от двух берегов: ![]() (29)
(29)
Из граничных условий (28) находим
 ,
, 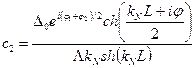 (30),
где
(30),
где ![]() .
.
Подставляя полученное решение в формулу (6) для тока (при A=0), найдём
![]() ,
, ![]() (31).
(31).
— ток не зависит от точки, в которой его вычисляют, как и должно быть. Интерференция
параметров порядка, приходящих от двух берегов, приводит к возникновению комбинации
![]() . В пределе длинного контакта, т.е.
при
. В пределе длинного контакта, т.е.
при ![]() критический ток экспоненциально мал:
критический ток экспоненциально мал:
![]() .
.

§5. Теория Асламазова и Ларкина
Теперь я хочу проанализировать случай короткого и грязного
сужения: ![]() , (32), где
, (32), где ![]() - мейсснеровская глубина проникновения
магнитного поля в сверхпроводник. Основа понимания того, как происходит эффект Джозефсона
в таких слабых связях, была заложена теорией Асламазова и Ларкина.
- мейсснеровская глубина проникновения
магнитного поля в сверхпроводник. Основа понимания того, как происходит эффект Джозефсона
в таких слабых связях, была заложена теорией Асламазова и Ларкина.
Малость ![]() позволяет существенно упростить
уравнения ГЛ. В первых, соотношение
позволяет существенно упростить
уравнения ГЛ. В первых, соотношение ![]() даёт возможность
в векторном потенциале
даёт возможность
в векторном потенциале ![]() , который должен в принципе
рассчитываться из уравнений Максвелла совместно с (4), пренебречь вкладом от токов
через слабую связь. Оставшуюся часть,
, который должен в принципе
рассчитываться из уравнений Максвелла совместно с (4), пренебречь вкладом от токов
через слабую связь. Оставшуюся часть, ![]() отражающую
вклад удалённых источников поля, можно представить в виде градиента некоторой
скалярной функции (т.к. для удалённых источников
отражающую
вклад удалённых источников поля, можно представить в виде градиента некоторой
скалярной функции (т.к. для удалённых источников ![]() в
области контакта). Но поскольку величина
в
области контакта). Но поскольку величина ![]() всегда
определена с точностью до такого градиента, можно выбрать калибровку
всегда
определена с точностью до такого градиента, можно выбрать калибровку![]() , включая тем самым влияние внешних
полей в фазу ∆. Во-вторых, при
, включая тем самым влияние внешних
полей в фазу ∆. Во-вторых, при ![]() можно пренебречь
в уравнении (4) всеми членами, кроме градиентного, поскольку его величина имеет
порядок
можно пренебречь
в уравнении (4) всеми членами, кроме градиентного, поскольку его величина имеет
порядок ![]() (т.к. в сужении ∆ меняется на
длине
(т.к. в сужении ∆ меняется на
длине ![]() на величину порядка
на величину порядка ![]() ) в то время как остальные члены порядка
) в то время как остальные члены порядка
![]() . Это означает, что по порядку величины
градиентный член больше остальных в
. Это означает, что по порядку величины
градиентный член больше остальных в ![]() раз. Таким образом,
уравнение (4) сводится просто к уравнению Лапласа:
раз. Таким образом,
уравнение (4) сводится просто к уравнению Лапласа: ![]() ,
(33)
,
(33)
что позволяет решить задачу до конца даже при произвольной форме слабой связи.
Условие больших градиентов физически следует из того, что большим куперовским парам
с размерами порядка ![]() трудно проникнуть в узкое
сужение с размерами много меньше, чем
трудно проникнуть в узкое
сужение с размерами много меньше, чем ![]() .
Это уравнение нужно решать с граничными условиями:
.
Это уравнение нужно решать с граничными условиями:
 , соответственно в глубине берега
1 и 2. (34),
, соответственно в глубине берега
1 и 2. (34),
![]() ,
(35), где
,
(35), где
![]() — граница слабой связи,
— граница слабой связи,
![]() — нормаль к этой поверхности.
— нормаль к этой поверхности.
Последнее условие есть частный случай
(12). Как было замечено в работе Асламазова–Ларкина и можно убедиться прямой подстановкой,
решение (единственное) краевой задачи (33)–(35) имеет вид ![]() (36), где
(36), где
![]() — действительная функция координат,
удовлетворяющая следующей краевой задаче:
— действительная функция координат,
удовлетворяющая следующей краевой задаче:
![]() ,
, ![]() ,
(37)
,
(37)
![]() в глубине
соответственно берега 1 или 2. (38)
в глубине
соответственно берега 1 или 2. (38)
Подставляя решение (36) в (6), получаем для плотности сверхпроводящего тока:
![]() .
(39)
.
(39)
Таким образом, плотность тока в каждой точке слабой связи и, следовательно,
полный ток пропорциональны ![]() — аналогично
случаю туннельного контакта.
— аналогично
случаю туннельного контакта.
Выражение (39) для плотности сверхпроводящего
тока содержит функцию ![]() , которую при произвольной
форме границы найти нельзя. Однако, даже не зная эту функцию, можно выразить полный
сверхпроводящий ток через сопротивление контакта в нормальном состоянии. Для этого
заметим, что через функцию
, которую при произвольной
форме границы найти нельзя. Однако, даже не зная эту функцию, можно выразить полный
сверхпроводящий ток через сопротивление контакта в нормальном состоянии. Для этого
заметим, что через функцию ![]() выражается
также ток
выражается
также ток ![]() через ту же самую слабую связь в нормальном
состоянии. Обозначим скалярный потенциал буквой
через ту же самую слабую связь в нормальном
состоянии. Обозначим скалярный потенциал буквой ![]() .
Согласно уравнениям Максвелла, он удовлетворяет уравнению Пуассона
.
Согласно уравнениям Максвелла, он удовлетворяет уравнению Пуассона ![]() , где
, где ![]() —
плотность заряда в проводнике.
—
плотность заряда в проводнике.
В проводниках с большой точностью выполняется
закон электронейтральности (заряд электронов компенсируется зарядом ионов), поэтому
![]() и
и ![]() в
каждой точке проводника, даже когда течёт ток. Очевидно, что решение краевой задачи
для скалярного потенциала
в
каждой точке проводника, даже когда течёт ток. Очевидно, что решение краевой задачи
для скалярного потенциала ![]() :
:
![]() ,
, ![]() ,
(40)
,
(40)
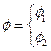 , соответственно
в глубине берега 1 или 2. (41).
, соответственно
в глубине берега 1 или 2. (41).
Записывается аналогично (36) с той же самой функцией![]() :
:
![]() ,
(42).
,
(42).
и поэтому ток в нормальном состоянии:
![]() ,
(43), где
,
(43), где ![]() .
.
Для вычисления полного тока через контакт мы можем проинтегрировать
это выражение по любому поперечному сечению ![]() :
:
![]() ,
(44),
,
(44),
что должно совпадать
с обычным законом Ома: ![]() , следовательно, мы получаем
формулу для сопротивления контакта в нормальном состоянии:
, следовательно, мы получаем
формулу для сопротивления контакта в нормальном состоянии: ![]() (45).
(45).
Теперь интегрируя (39) по
тому же самому сечению ![]() ,мы можем записать результат
в виде
,мы можем записать результат
в виде ![]() с критическим током, имеющим такой
же вид, как и в туннельном контакте (формула (18)):
с критическим током, имеющим такой
же вид, как и в туннельном контакте (формула (18)): ![]() .
(46)
.
(46)
Теория Асламазова–Ларкина не только описывает эффект Джозефсона
в слабых связях, но и даёт возможность очень ясно усмотреть его физическое происхождение.
Действительно, формула (36) показывает, что в области слабой связи (где ![]() ) параметр порядка есть линейная суперпозиция
двух членов, каждый из которых пропорционален значению
) параметр порядка есть линейная суперпозиция
двух членов, каждый из которых пропорционален значению ![]() в
одном из берегов и координатному множителю, плавно спадающему при удалении от данного
берега вглубь слабой связи. Таким образом, внутри слабой связи происходит интерференция
двух волновых функций, источниками которых являются конденсаты куперовских пар в
сверхпроводящих берегах. Такая интерференция немедленно даёт ток
в
одном из берегов и координатному множителю, плавно спадающему при удалении от данного
берега вглубь слабой связи. Таким образом, внутри слабой связи происходит интерференция
двух волновых функций, источниками которых являются конденсаты куперовских пар в
сверхпроводящих берегах. Такая интерференция немедленно даёт ток ![]() т.е. эффект Джозефсона.
т.е. эффект Джозефсона.
Глава 4. Нестационарный эффект Джозефсона в туннельных структурах
§1. Общие свойства
Эффект Джозефсона, рассмотренный в разделе 4, называют стационарным, т.к. ток через контакт не меняется во времени. Ток через контакт течёт в отсутствие напряжения на контакте и поэтому является бездиссипативным (не сопровождается выделением джоулева тепла).
Основной результат этого раздела — формула (18) — сразу же вызывает несколько вопросов:
1) что будет, если к такому контакту приложить напряжение,
2) что будет, если через контакт пустить ток, превышающий критический ток
![]() .
.
Оказывается, что это две стороны одного и того же вопроса. Дело в том, что через джозефсоновский контакт могут течь два разных вида токов: бездиссипативный сверхпроводящий ток куперовских пар и обычный диссипативный ток отдельных электронов (сопровождающийся выделением джоулева тепла). Величина каждого из токов определяется условиями, которые мы задаём в берегах контакта.
Стационарный эффект Джозефсона имеет место в случае, когда в берегах задана фиксированная разность сверхпроводящих фаз (пример экспериментальной реализации этого случая — рис.2). В таких условиях весь ток через контакт — сверхпроводящий, и он не зависит от времени.
Пусть теперь к туннельному контакту приложена от внешнего источника
некоторая разность потенциалов ![]() .Тогда в контакте
возникает электрическое поле
.Тогда в контакте
возникает электрическое поле ![]() , которое будем описывать
скалярным потенциалом
, которое будем описывать
скалярным потенциалом ![]() ,так что
,так что ![]() . Влияние этого поля на сверхпроводящий
ток через контакт можно выяснить уже на основании требований калибровочной инвариантности,
т.е. на основании того, что скалярный потенциал
. Влияние этого поля на сверхпроводящий
ток через контакт можно выяснить уже на основании требований калибровочной инвариантности,
т.е. на основании того, что скалярный потенциал ![]() (вместе
с векторным потенциалом
(вместе
с векторным потенциалом![]() ) определены неоднозначно
и могут быть подвергнуты калибровочному преобразованию, при котором никакие физические
величины не меняются.
) определены неоднозначно
и могут быть подвергнуты калибровочному преобразованию, при котором никакие физические
величины не меняются.
В отсутствие
поля (при ![]() ) фаза волновой функции независит от
времени:
) фаза волновой функции независит от
времени: ![]() , что соответствует стационарному эффекту
Джозефсона. Для обобщения этого равенства на случай наличия электрического поля
заметим, что общее соотношение должно быть инвариантно по отношению к калибровочному
преобразованию скалярного потенциала:
, что соответствует стационарному эффекту
Джозефсона. Для обобщения этого равенства на случай наличия электрического поля
заметим, что общее соотношение должно быть инвариантно по отношению к калибровочному
преобразованию скалярного потенциала: ![]() ,
(47)
,
(47)
не затрагивающему векторный потенциал (который предполагается независящим от времени). При этом волновые функции электронов домножаются на фазовые множители:
![]() .
(48)
.
(48)
Сверхпроводящий параметр порядка является волновой функцией пар электронов
(куперовских пар), поэтому связан с произведением волновых функций двух электронов,
следовательно, его фаза преобразуется как ![]() (49)
(49)
Отсюда ясно, что калибровочно инвариантным будет соотношение
![]() (50),
(50),
переходящее в ![]() при
при![]() .
Фазу
.
Фазу ![]() и потенциал
и потенциал ![]() в этом соотношении следует снабдить
индексами 1, 2, т.к. оно должно выполняться для каждого из сверхпроводящих берегов.
После этого, вычитая одно из другого, получаем
в этом соотношении следует снабдить
индексами 1, 2, т.к. оно должно выполняться для каждого из сверхпроводящих берегов.
После этого, вычитая одно из другого, получаем
![]() ,
(51), где
,
(51), где ![]() ,
, ![]()
Этот фундаментальный результат теории эффекта Джозефсона, связывающий скорость изменения во времени разности фаз между берегами контакта с напряжением на контакте, очень важен для дальнейшего рассмотрения. Несмотря на кажущуюся простоту его вывода, он основан на глубоком понимании микроскопической природы сверхпроводящего состояния, связанной с образованием куперовских пар, — именно из этих соображений была получена формула (49).
В случае постоянного электрического поля (51) даёт
![]() (52), где
(52), где ![]() — константа. Поскольку сверхпроводящий
ток через контакт является периодической функцией разности фаз
— константа. Поскольку сверхпроводящий
ток через контакт является периодической функцией разности фаз ![]() , а разность фаз зависит от времени
линейно, можно сразу придти к выводу о том, что при приложении к джозефсоновскому
контакту постоянной разности потенциалов
, а разность фаз зависит от времени
линейно, можно сразу придти к выводу о том, что при приложении к джозефсоновскому
контакту постоянной разности потенциалов ![]() возникает
нестационарный эффект Джозефсона: сверхпроводящий ток становится переменным с частотой
возникает
нестационарный эффект Джозефсона: сверхпроводящий ток становится переменным с частотой
![]() (53).
(53).
При этом явная зависимость тока от времени — вопрос более сложный, и ответ
на него зависит от величины разности потенциалов. Проще всего случай, когда разность
потенциалов мала, так что джозефсоновская частота ![]() много
меньше характерной для сверхпроводимости частоты
много
меньше характерной для сверхпроводимости частоты ![]() :
:
![]() (54)
(54)
В таком случае нормальная компонента тока (неизбежно возникающая
при наличии разности потенциалов) мала, и почти весь ток является сверхпроводящим,
зависящим от времени в соответствии с (18), куда нужно теперь подставить зависящую
от времени разность фаз (52): ![]() .
(55)
.
(55)
Потребляемая в контакте мощность даётся произведением ![]() ; её среднее (по времени) значение
равно нулю, т.е. систематическая затрата энергии от внешнего источника отсутствует
— как и должно быть для сверхпроводящего тока, несвязанного с диссипацией
энергии (при этом, конечно, малый нормальный ток, которым мы пренебрегли, будет
приводить к слабой диссипации).
; её среднее (по времени) значение
равно нулю, т.е. систематическая затрата энергии от внешнего источника отсутствует
— как и должно быть для сверхпроводящего тока, несвязанного с диссипацией
энергии (при этом, конечно, малый нормальный ток, которым мы пренебрегли, будет
приводить к слабой диссипации).
Для обсуждения более общей ситуации, когда нормальный ток не обязательно мал по сравнению со сверхпроводящим, мы рассмотрим контакт в немного другом режиме — незаданного напряжения, а заданного тока.
§2. Резистивная модель
Предположим, что контакт находится в режиме заданного тока,
а напряжение подстраивается под него в соответствии со свойствами системы (такой
режим часто изучается в эксперименте). Пока заданный ток ![]() меньше критического
меньше критического ![]() весь ток переносится куперовскими парами
(т.е. сверхпроводящим током). Если же
весь ток переносится куперовскими парами
(т.е. сверхпроводящим током). Если же ![]() ,
то куперовские пары уже не могут обеспечить такой ток, и в дополнение к сверхпроводящему
току возникает нормальная компонента, а значит, и напряжение на контакте, т.к. нормальная
компонента связана с диссипацией.
,
то куперовские пары уже не могут обеспечить такой ток, и в дополнение к сверхпроводящему
току возникает нормальная компонента, а значит, и напряжение на контакте, т.к. нормальная
компонента связана с диссипацией.
При ![]() сверхпроводимость
в берегах, а также сверхпроводящая связь между берегами не разрушаются —
нормальная компонента тока появляется в дополнение к сверхпроводящей. Эта ситуация
не имеет отношения к так называемому току распаривания объёмного сверхпроводника,
связанному с тем, что куперовские пары начинают разрушаться при определённой скорости
движения, — в таком случае при превышении током соответствующего критического значения
сверхпроводимость разрушалась бы полностью. В джозефсоновском же контакте речь идёт
именно о свойствах контакта, и ток
сверхпроводимость
в берегах, а также сверхпроводящая связь между берегами не разрушаются —
нормальная компонента тока появляется в дополнение к сверхпроводящей. Эта ситуация
не имеет отношения к так называемому току распаривания объёмного сверхпроводника,
связанному с тем, что куперовские пары начинают разрушаться при определённой скорости
движения, — в таком случае при превышении током соответствующего критического значения
сверхпроводимость разрушалась бы полностью. В джозефсоновском же контакте речь идёт
именно о свойствах контакта, и ток ![]() мал в силу большого
сопротивления туннельной границы, в частности гораздо меньше тока распаривания
берегов.
мал в силу большого
сопротивления туннельной границы, в частности гораздо меньше тока распаривания
берегов.
Итак, оказывается, что при ![]() на
контакте возникает напряжение. Фундаментальным результатом теории эффекта Джозефсона
является соотношение (51) между напряжением на контакте и скоростью изменения во
времени разности фаз между берегами.
на
контакте возникает напряжение. Фундаментальным результатом теории эффекта Джозефсона
является соотношение (51) между напряжением на контакте и скоростью изменения во
времени разности фаз между берегами.
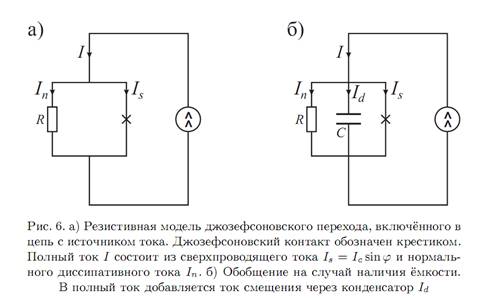
Рассмотрим нестационарный эффект Джозефсона в рамках так
называемой резистивной модели, которая прямо вытекает из этой картины. Полный ток
![]() через систему является суммой сверхпроводящего
тока
через систему является суммой сверхпроводящего
тока ![]() определяемого формулой (18), и нормального
определяемого формулой (18), и нормального
![]() тока, где
тока, где ![]() —
сопротивление контакта в нормальном состоянии. Таким образом, джозефсоновский контакт
можно представить в виде параллельного соединения идеального (бездиссипативного)
джозефсоновского контакта и сопротивления
—
сопротивление контакта в нормальном состоянии. Таким образом, джозефсоновский контакт
можно представить в виде параллельного соединения идеального (бездиссипативного)
джозефсоновского контакта и сопротивления ![]() (см.рис.6а).
Используя соотношение (51), получаем уравнение
(см.рис.6а).
Используя соотношение (51), получаем уравнение
![]() ,
(56)
,
(56)
определяющее динамику фазы при заданном токе ![]() через
контакт. Обратите внимание, что вся микроскопическая информация о контакте содержится
в величинах
через
контакт. Обратите внимание, что вся микроскопическая информация о контакте содержится
в величинах ![]() и
и ![]() ,
в то время как резистивная модель принимает эти величины как данные и изучает поведение
макроскопической характеристики контакта — разности фаз
,
в то время как резистивная модель принимает эти величины как данные и изучает поведение
макроскопической характеристики контакта — разности фаз ![]() ,
которая характеризует сверхпроводящее состояние контакта в целом, т.е. содержит
информацию только о фазе сверхпроводящего конденсата, состоящего из огромного количества
электронов.
,
которая характеризует сверхпроводящее состояние контакта в целом, т.е. содержит
информацию только о фазе сверхпроводящего конденсата, состоящего из огромного количества
электронов.
Уравнение (56) на функцию ![]() интегрируется
в элементарных функциях, после чего формула (51) при подходящем выборе начала
отсчёта времени даёт
интегрируется
в элементарных функциях, после чего формула (51) при подходящем выборе начала
отсчёта времени даёт
![]() , (57) где
, (57) где ![]() (58).
(58).
Итак, если заданный постоянный ток ![]() через контакт превышает критический
ток контакта
через контакт превышает критический
ток контакта ![]() на нём возникает напряжение
на нём возникает напряжение ![]() , периодически зависящее от времени.
Следовательно, джозефсоновский контакт начинает излучать электромагнитные волны
— это явление называется джозефсоновской генерацией.
, периодически зависящее от времени.
Следовательно, джозефсоновский контакт начинает излучать электромагнитные волны
— это явление называется джозефсоновской генерацией.
Усреднение формулы (57) по времени приводит к соотношению
![]() , (59) имеющему простую физическую
интерпретацию: при переходе с одной стороны контакта на другую куперовские пары
в среднем приобретают энергию
, (59) имеющему простую физическую
интерпретацию: при переходе с одной стороны контакта на другую куперовские пары
в среднем приобретают энергию![]() , которая затем выделяется
в виде кванта электромагнитного излучения с частотой
, которая затем выделяется
в виде кванта электромагнитного излучения с частотой ![]() .
.
Вольтметр постоянного тока, подключенный к переходу, будет
показывать именно среднее напряжение ![]() ,
поэтому полученная с его помощью вольт-амперная характеристика будет иметь вид
,
поэтому полученная с его помощью вольт-амперная характеристика будет иметь вид ![]() ,(60) следующий из формул (59) и (58)
и показанный на рис. 7 а.
,(60) следующий из формул (59) и (58)
и показанный на рис. 7 а.
Если ток ![]() через переход лишь немного
превышает
через переход лишь немного
превышает ![]() , то в основном он течёт в виде сверхпроводящего
тока
, то в основном он течёт в виде сверхпроводящего
тока ![]() через джозефсоновский элемент на эквивалентной
схеме рис.6а, в то время как нормальный ток мал. Наоборот, при
через джозефсоновский элемент на эквивалентной
схеме рис.6а, в то время как нормальный ток мал. Наоборот, при ![]() почти весь ток течёт через резистор
почти весь ток течёт через резистор
![]() и вольт-амперная характеристика на
этом участке выходит на линейную характеристику перехода в нормальном состоянии.
и вольт-амперная характеристика на
этом участке выходит на линейную характеристику перехода в нормальном состоянии.

Для джозефсоновского контакта наиболее энергетически выгодным является состояние
с разностью фаз, равной нулю (или целому кратному![]() ),—
при этом ток через контакт отсутствует. Если же разность фаз
),—
при этом ток через контакт отсутствует. Если же разность фаз ![]() ненулевая и через контакт течёт некоторый
ток
ненулевая и через контакт течёт некоторый
ток![]() ,то это означает, что в контакте запасена
энергия. Найти её можно следующим образом. Будем отсчитывать энергию от энергии
при
,то это означает, что в контакте запасена
энергия. Найти её можно следующим образом. Будем отсчитывать энергию от энергии
при ![]() и представив, что ток
и представив, что ток ![]() возник в результате медленного нарастания
разности фаз от нуля до
возник в результате медленного нарастания
разности фаз от нуля до ![]() в течение некоторого
времени
в течение некоторого
времени ![]() . Если фаза менялась во времени, значит,
на контакте возникало напряжение, и запасённую энергию можно найти как
. Если фаза менялась во времени, значит,
на контакте возникало напряжение, и запасённую энергию можно найти как 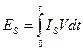 (61), где
(61), где ![]() определяется по формуле (51).
определяется по формуле (51).
Подставляя сюда также обычное джозефсоновское соотношение ![]() и переходя к интегрированию по
и переходя к интегрированию по ![]() , получаем
, получаем![]() (62) , где
(62) , где ![]() (63).
(63).
Энергию (62) называют джозефсоновской энергией. Джозефсоновский переход можно рассматривать как нелинейный индуктивный элемент, запасающий энергию при изменении тока через него.
Формула
(62) для зависимости ![]() применима для случая синусоидальной
зависимости сверхпроводящего тока от разности фаз. Это так в туннельном контакте,
но в общем случае зависимость
применима для случая синусоидальной
зависимости сверхпроводящего тока от разности фаз. Это так в туннельном контакте,
но в общем случае зависимость ![]() может быть более
сложной. Мы легко можем, однако, выразить сверхпроводящий ток через джозефсоновскую
энергию в общем случае. Для этого продифференцируем формулу (61) по времени,
что даёт
может быть более
сложной. Мы легко можем, однако, выразить сверхпроводящий ток через джозефсоновскую
энергию в общем случае. Для этого продифференцируем формулу (61) по времени,
что даёт ![]() и далее
и далее ![]() . В результате напряжение сокращается,
и мы получаем общее соотношение
. В результате напряжение сокращается,
и мы получаем общее соотношение ![]() .
(64)
.
(64)
Обсуждение джозефсоновской энергии ![]() относится непосредственно к контакту.
Если же рассматривать джозефсоновский контакт не сам по себе, а включённым в цепь
с источником тока, то при вычислении свободной энергии цепи нужно также учитывать
энергию, затрачиваемую источником тока:
относится непосредственно к контакту.
Если же рассматривать джозефсоновский контакт не сам по себе, а включённым в цепь
с источником тока, то при вычислении свободной энергии цепи нужно также учитывать
энергию, затрачиваемую источником тока:
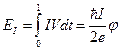 (65)
(65)
Таким образом, свободная энергия цепи для случая заданного
тока как функция разности фаз на контакте даётся формулой ![]() (66)
(66)
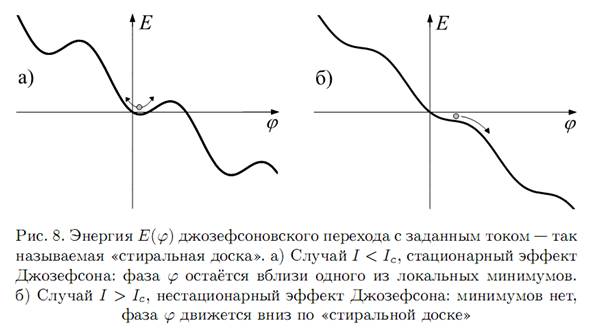
которая проиллюстрирована
на рис. 8. Такую форму кривой, получающуюся из формулы (66), часто называют «стиральной
доской». Обсуждение эффекта Джозефсона на языке ![]() становится
весьма наглядным. При
становится
весьма наглядным. При ![]() фаза
фаза ![]() находится в локальном минимуме свободной
энергии, что соответствует стационарному эффекту Джозефсона (см. рис. 8а). С увеличением
тока
находится в локальном минимуме свободной
энергии, что соответствует стационарному эффекту Джозефсона (см. рис. 8а). С увеличением
тока ![]() средний наклон «стиральной доски» возрастает,
а глубина локальных минимумов уменьшается. При
средний наклон «стиральной доски» возрастает,
а глубина локальных минимумов уменьшается. При ![]() локальные
минимумы пропадают, и фаза начинает «скатываться» вниз по «стиральной доске» — значит,
локальные
минимумы пропадают, и фаза начинает «скатываться» вниз по «стиральной доске» — значит,
![]() непрерывно меняется во времени, следовательно,
на контакте возникает напряжение — это и есть нестационарный эффект Джозефсона (см.
рис. 8б).
непрерывно меняется во времени, следовательно,
на контакте возникает напряжение — это и есть нестационарный эффект Джозефсона (см.
рис. 8б).
§3. Резистивная модель с ёмкостью
При составлении эквивалентной схемы джозефсоновского контакта, изображённой на рис. 6а, надо учесть ещё один фактор, который может оказаться важным: как видно из самого устройства джозефсоновского контакта, в котором два берега разделены прослойкой диэлектрика, такая конструкция напоминает конденсатор, следовательно, должна обладать некоторой ёмкостью. Если данная ёмкость мала (с чем её надо сравнивать, станет ясно из дальнейшего рассмотрения), то ею можно пренебречь, и применимо предыдущее рассмотрение. В этом же разделе мы обсудим, к чему приводит наличие ёмкости.
Итак, в общем случае в рамках резистивной модели необходимо
дополнить эквивалентную схему параллельно включённой ёмкостью С (см.рис.6б). Хотя
постоянный ток через конденсатор невозможен, тем не менее, через него может течь
переменный ток смещения: ![]() ,
(67)
,
(67)
связанный с перезарядкой
обкладок конденсатора. Этот ток необходимо добавить в левую часть соотношения (56),
одновременно выразив напряжение через разность фаз по общей формуле (51). Домножая
также обе стороны на ![]() , получаем следующее уравнение
на функцию
, получаем следующее уравнение
на функцию ![]() :
: 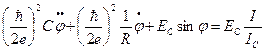 (68)
(68)
которое имеет такой
же вид, как и уравнение движения маятника под действием вынуждающей силы и при наличии
трения. Кроме того, отождествляя ![]() с линейной координатой
с линейной координатой
![]() , мы можем смотреть на это уравнение
как на уравнение движения частицы массой
, мы можем смотреть на это уравнение
как на уравнение движения частицы массой ![]() при
наличии трения с коэффициентом трения
при
наличии трения с коэффициентом трения ![]() в
периодическом потенциале
в
периодическом потенциале ![]() под действием внешней
силы
под действием внешней
силы ![]() . Собственная частота малых колебаний
вблизи одного из минимумов потенциала равна
. Собственная частота малых колебаний
вблизи одного из минимумов потенциала равна ![]() (69)
(69)
и называется в джозефсоновском случае плазменной частотой перехода. Плазменная частота может рассматриваться также как резонансная частота
![]() (70)
(70)
контура с ёмкостью
![]() «собственной индуктивностью» джозефсоновского
перехода:
«собственной индуктивностью» джозефсоновского
перехода:
![]() (71)
(71)
«Масса», определяющая
инерционное поведение перехода при изменении ![]() ,
связана с величиной ёмкости
,
связана с величиной ёмкости ![]() .Таким образом, рассмотренный
в предыдущем разделе случай соответствует безмассовой частице. К чему же теперь
приводит наличие массы? Предположим, что мы сначала увеличиваем ток
.Таким образом, рассмотренный
в предыдущем разделе случай соответствует безмассовой частице. К чему же теперь
приводит наличие массы? Предположим, что мы сначала увеличиваем ток ![]() от нуля до бесконечности, а за тему
уменьшаем обратно до нуля. Как и раньше, массивная частица начнёт непрерывно двигаться
при наклоне «стиральной доски», соответствующем
от нуля до бесконечности, а за тему
уменьшаем обратно до нуля. Как и раньше, массивная частица начнёт непрерывно двигаться
при наклоне «стиральной доски», соответствующем ![]() .
Правда, в отличие от безмассовой частицы, которая при
.
Правда, в отличие от безмассовой частицы, которая при ![]() ,
слегка превышающем
,
слегка превышающем ![]() движется очень медленно,
частица с конечной массой сразу же разгонится до некоторой конечной скорости (т.е.
с увеличением тока при
движется очень медленно,
частица с конечной массой сразу же разгонится до некоторой конечной скорости (т.е.
с увеличением тока при ![]() на контакте скачком возникнет
конечное напряжение). При дальнейшему увеличении наклона скорость будет расти. Существенная
особенность массивной частицы проявится при уменьшении тока. Уменьшив ток до, мы
снова получим частицу, движущуюся с конечной скоростью. В связи с инерцией частицы
остановить её можно, только несколько уменьшив угол наклона по сравнению с критическим,
т.е. при некотором «токе возврата». Ток возврата тем меньше, чем выше ёмкость («масса»)
и чем выше сопротивление (т.е. чем меньше «вязкость»).
на контакте скачком возникнет
конечное напряжение). При дальнейшему увеличении наклона скорость будет расти. Существенная
особенность массивной частицы проявится при уменьшении тока. Уменьшив ток до, мы
снова получим частицу, движущуюся с конечной скоростью. В связи с инерцией частицы
остановить её можно, только несколько уменьшив угол наклона по сравнению с критическим,
т.е. при некотором «токе возврата». Ток возврата тем меньше, чем выше ёмкость («масса»)
и чем выше сопротивление (т.е. чем меньше «вязкость»).
Таким
образом, наличие ёмкости у джозефсоновского контакта при водит к гистерезису его
вольт-амперной характеристики (см. рис.7б — зависимость ![]() различна
для случаев увеличения и уменьшения
различна
для случаев увеличения и уменьшения ![]() ). Количественно
ток возврата и гистерезисные свойства определяются величиной параметра МакКамбера:
). Количественно
ток возврата и гистерезисные свойства определяются величиной параметра МакКамбера:
![]() (72)
(72)
С помощью параметра ![]() и характерной джозефсоновской
частоты
и характерной джозефсоновской
частоты ![]() мы можем записать (68) в более компактном
виде:
мы можем записать (68) в более компактном
виде:  (73).
(73).
При ![]() ёмкостным членом можно пренебречь.
В этом случае уравнение сводится к виду (56), и вольт-амперная характеристика
имеет однозначный вид (60). С увеличением
ёмкостным членом можно пренебречь.
В этом случае уравнение сводится к виду (56), и вольт-амперная характеристика
имеет однозначный вид (60). С увеличением ![]() возникает
гистерезис с током возврата
возникает
гистерезис с током возврата ![]() , который убывает
с ростом и стремится к нулю в пределе
, который убывает
с ростом и стремится к нулю в пределе ![]() т.е.
в этом пределе возвратная часть вольт- амперной характеристики становится линейной).
т.е.
в этом пределе возвратная часть вольт- амперной характеристики становится линейной).
Глава 5. Использование сверхпроводимости.
Идея
высокотемпературной сверхпроводимости (ВТСП) в органических соединениях
была выдвинута в 1950г. Ф.Лондоном и лишь спустя 14 лет появился
отклик на эту идею в работах американского физика В.Литтла, вызвавший
критические отзывы, отрицающие возможность ВТСП в неметаллических
системах. Таким образом, хотя идея ВТСП родилась в работе Ф. Лондона в
1950г., годом рождения проблемы следует считать время появления первых,
пока, правда, малочисленных потоков информации по ВТСП - 1964г.. Если
рассмотреть эволюцию температуры сверхпроводящего перехода, то станет ясно,
что рост температуры сверхпроводящего перехода приводил к возможности
использования хладагентов с все более высокой температурой кипения
(жидкий гелий, водород, неон, азот). Хотя до азотных температур перехода,
открытых недавно в металлокерамиках, практически использовался для
охлаждения жидкий гелий, однако скачки в росте температуры перехода дают
право положить их в основу периодизации ВТСП о гелиевом, водородном, неоновом
и, наконец, азотном периодах ВТСП. Так ![]() сменился
сменился
![]() , затем наибольшая температура была
обнаружена в 1973-81гг. у
, затем наибольшая температура была
обнаружена в 1973-81гг. у ![]() (23,9 K), которая оставалась рекордной вплоть
до сверхпроводимости металлокерамиками.
(23,9 K), которая оставалась рекордной вплоть
до сверхпроводимости металлокерамиками. ![]() при
при
![]() в 1986г., вырастая до 100 К
на материале
в 1986г., вырастая до 100 К
на материале ![]() . Ключевым для проблемы
ВТСП является вопрос критической температуры от характеристики вещества.
. Ключевым для проблемы
ВТСП является вопрос критической температуры от характеристики вещества.
С открытием в 1986 нового класса сверхпроводящих материалов с более высокими, чем ранее критическими температурами, во всем мире развернулись работы по изучению по изучению свойств ВТСП с целью определения возможности их применения в различных областях науки и техники. Интерес к ВТСП объясняется в первую очередь тем, что повышение рабочей температуры до азотной позволит существенно упростить и удешевить системы криогенного обеспечения, повысить их надежность. Для успешного применения ВТСП в сильноточных устройствах (соленоидах, накопителях энергии, электромагнитах, транспорте с магнитным подвесом) необходимо решить ряд вопросов. Одной из важнейших проблем при создании сильноточных устройств с использованием ВТСП является проблема обеспечения устойчивой работы обмоток с током. Проблема стабилизации ВТСП включает в себя несколько аспектов. Внутренним свойством сверхпроводимости является скачкообразный характер проникновения в них магнитного поля. Этот процесс сопровождается выделением части запасенной энергии магнитного поля при его распределении. Поэтому, наиболее важное направление стабилизации сверхпроводников - их стабилизация против сигналов потока. Кроме того, проводники, внутренне стабилизированные против сигналов потока, при работе подвергаются действию различного рода возмущений как механического, так и электромагнитного характера, тоже сопровождающиеся выделением энергии.
Вопросы различных применений сверхпроводимости стали обсуждаться практически сразу же после открытия этого поразительного явления. Еще Камерлинг – Оннес считал, что с помощью сверхпроводников можно создавать экономичные установки для получения сильных магнитных полей. Однако реальное использование сверхпроводимости началось лишь в конце 50-х – начале 60-х годов. В настоящее время уже работают сверхпроводящие магниты различных размеров и формы. Их применение вышло за рамки чисто научных исследований, и сегодня они широко используются в лабораторной практике, в ускорительной технике, томографах, установках для управляемой термоядерной реакции. С помощью сверхпроводимости стало возможным повысить чувствительность некоторых измерительных приборов. Особенно следует подчеркнуть влияние сквидов в технику, в том числе и в современную медицину. Сверхпроводимость стала большой отдельной отраслью промышленности. Открытие высокотемпературной сверхпроводимости создало предпосылки к более широкому внедрению в повседневную практику различных сверхпроводящих устройств.
Наибольшее применение сверхпроводники нашли в настоящее время в области создания сильных магнитных полей. Современная промышленность производит из сверхпроводников второго рода разнообразные провода и кабели, используемые для изготовления обмоток магнитов. Преимущества сверхпроводящих магнитов очевидны. С помощью сверхпроводников получают значительно более сильные магнитные поля, чем при использовании железных магнитов. Сверхпроводящие магниты являются и более экономичными.
Следует отметить, что максимально возможное магнитное поле, создаваемое сверхпроводящими магнитами, ограничено верхним пределом для плотности тока (критическими токами). Критический ток определяется, как правило, технологией приготовления проводников, а не верхним критическим полем материала.
Сверхпроводящие магниты обладают еще одним преимуществом по сравнению с обычными. Они могут работать в короткозамкнутом режиме, когда поле заморожено в объеме, что обеспечивает практически не зависящую от времени стабильность поля. Это свойство чрезвычайно важно при измерениях в веществе ядерного магнитного и электронного парамагнитного резонансов, в томографах и т.п.
В сверхпроводящих соленоидах с большим объемом поля запасенная энергия достаточно велика. В случае перехода катушки в нормальное состояние эта энергия превратиться в тепло. Если при переходе в нормальное состояние вся энергия бесконтрольно превратиться в тепло, то это может привести к полному разрушению магнита. Во-избежании таких катастрофических последствий самопроизвольного перехода катушки в нормальное состояние соленоиды, в особенности большие, снабжаются специальными защитными устройствами, предназначенными для быстрого вывода запасенной энергии.
Очень заманчиво попытаться использовать сверхпроводники в электротехнике и энергетике. Ведь в настоящее время потери на джоулево тепло в проводящих проводах оцениваются величиной 30 - 40%, то есть более трети всей производимой энергии тратиться даром – на «отопление» Вселенной. Если же передавать электроэнергию по сверхпроводящим проводам с нулевым сопротивлением, то таких потерь не будет вообще. Это равносильно увеличению выработки электроэнергии более чем на треть. На основе сверхпроводников можно создавать электродвигатели и генераторы с высоким КПД и другими улучшенными рабочими характеристиками.
Если над металлическим кольцом с током поместить сверхпроводящую сферу, то на её поверхности в силу эффекта Мейснера индуцируется сверхпроводящий ток, что приводит к появлению сил отталкивания между кольцом и сферой, и сфера висит над кольцом. Подобный эффект механического отталкивания наблюдается и в том случае, когда над сверхпроводящим кольцом помещается постоянный магнит. Этот эффект, часто используемый для демонстраций явления сверхпроводимости, получил название «гроб Магомета», ибо, по преданию, гроб Магомета висел в пространстве без всякой поддержки.
Явление механического отталкивания применяется, в частности, для создания подшипников и опор без трения. Заманчива перспектива использования левитации сверхпроводника в транспорте. Речь идет о создании поезда на магнитной подушке, в котором будут полностью отсутствовать потери на трении о колею дороги. Модель такой сверхпроводящей дороги длиной 400м была создана в Японии еще в 70-х годах. Расчеты показывают, что поезд на магнитной подушке сможет развивать скорость до 500 км/ч. такой поезд будет «зависать» над рельсами на расстоянии 2 – 3 см, что и даст ему возможность разгоняться до указанных скоростей.
Широко используется в настоящее время сверхпроводящие, объемные резонаторы. С одной стороны, такие сверхпроводящие резонаторы позволяют получить высокую частотную избирательность. С другой стороны, сверхпроводящие резонаторы широко используются в сверхпроводящих ускорителях, позволяя существенно уменьшить мощность, требуемую для создания ускоряющего электрического поля. Как правило, сверхпроводящие резонаторы изготовляются из свинца либо из ниобия.
Одно из самых распространенных направлений прикладной сверхпроводимости – использование сквидов как в научных исследованиях, так и в различных технических областях. градиометры на основе сквидов реагируют чрезвычайно слабые магнитные поля, поэтому их уже сегодня эффективно используют в медицине и биологии для исследования полей живых организмов и человека. В геологии сквиды применяются для определения изменения силы гравитации в различных точках Земли. Такая информация нужна для поиска полезных ископаемых.
Наиболее перспективными направлениями широкого использования высокотемпературных сверхпроводников считаются криоэнергетика и криоэлектроника. В криоэнергетике уже разработана методика приготовления достаточно длинных проводов (до 1000 метров) проводов и кабелей на основе висмутовых ВТСП – материалов. Этого уже хватает для изготовления небольших двигателей со сверхпроводящей обмоткой, сверхпроводящих трансформаторов, индуктивностей и т.п. На основе этих материалов уже созданы сверхпроводящие соленоиды, обеспечивающие при температуре жидкого азота (77К) магнитные поля порядка 10 000Гс.
Темп технологических и прикладных исследований очень высок, так что, возможно, промышленность освоит выпуск изделий из высокотемпературных сверхпроводников раньше, чем будет достоверно выяснена природа сверхпроводимости в металлооксидных соединениях. Для технологии в первую очередь важен сам факт существования материалов, сверхпроводящих при температуре жидкого азота. Однако целенаправленное и осмысленное движение вперед, в том числе технологической сфере, невозможно без всестороннего исследования уже известных ВТСП, без понимания всех тонкостей высокотемпературной сверхпроводимости как интереснейшего физического явления. Тем более это относится к поиску новых сверхпроводников.
Я привела лишь несколько примеров практического использования сверхпроводимости. Не меньшее значение, конечно, имеют проблемы передачи электроэнергии на большие расстояния без потерь, создания накопителей энергии, защиты космических аппаратов от космического излучения и т.д. примеров научного и технического применения сверхпроводимости множество, но подобное изучение этих вопросов выходит за рамки данной работы.
§1. Контакт Джозефсона
Следующее практическое применение сверхпроводимости
относится к технике чувствительных электронных приборов. Экспериментальные
образцы приборов с контактом Джозефсона могут обнаруживать напряжения порядка
10![]() Вт. Магнитометры, способные
обнаруживать магнитные поля порядка 10
Вт. Магнитометры, способные
обнаруживать магнитные поля порядка 10![]() Гс,
используются при изучении магнитных материалов, а также в медицинских
магнитокардиографах. Чрезвычайно чувствительные детекторы вариаций силы тяжести
могут применяться в различных областях геофизики.
Гс,
используются при изучении магнитных материалов, а также в медицинских
магнитокардиографах. Чрезвычайно чувствительные детекторы вариаций силы тяжести
могут применяться в различных областях геофизики.
Техника сверхпроводимости и особенно контакты Джозефсона оказывают все большее влияние на метрологию. С помощью джозефсоновских контактов создан стандарт 1 В. Был разработан также первичный термометр для криогенной области, в которой резкие переходы в некоторых веществах используются для получения реперных (постоянных) точек температуры. Новая техника используется в компараторах тока, для измерений радиочастотной мощности и коэффициента поглощения, а также для измерений частоты. Она применяется также в фундаментальных исследованиях, таких, как измерение дробных зарядов атомных частиц и проверка теории относительности.
Сверхпроводимость будет широко использоваться в компьютерных технологиях. Здесь сверхпроводящие элементы могут обеспечивать очень малые времена переключения, ничтожные потери мощности при использовании тонкопленочных элементов и большие объемные плотности монтажа схем. Разрабатываются опытные образцы тонкопленочных джозефсоновских контактов в схемах, содержащих сотни логических элементов и элементов памяти.
Пример:
Патент США 3626391: Запоминающая матрица выполнена на запоминающих элементах, содержащих туннельные вентили (вентили туннельных криотронов) с использованием тока Джозефсона. Каждый запоминающий элемент состоит из двух устройств на основе эффекта Джозефсона, каждое из которых находится в отдельной ветви элемента. Предусмотрены также возбуждающие дешифраторы, использующие устройства на основе эффекта Джозефсона, для коммутации тока по различным шинам матрицы, связанные с запоминающими элементами. Направление тока, протекающего и запоминающем элементе, определяет его двоичное состояние.
§2. Сканирующая туннельная микроскопия
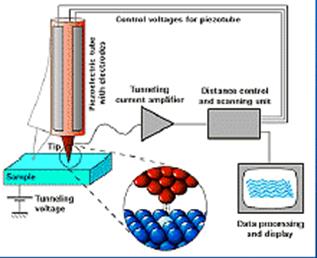
Это сканирующий туннельный микроскоп, созданный в отделении IBM в Цюрихе. Принцип его действия — туннельный эффект. Этот прибор работает, потому что работает квантовая механика. Как это действует? Есть образец, есть другое устройство, тип, которое вы подносите очень близко. Промежуток между образцом и типом представляет собой потенциальный барьер для электрона. Они могут через него туннелировать. Если вы увеличиваете расстояние, вероятность туннелирования очень быстро падает. А прохождение электронов — это электрический ток. И вы можете удерживать этот образец на таком расстоянии, чтобы ток оставался постоянным, для этого его нужно то - приближать, то удалять. И дальше это движение вдоль образца прорисовывает вам распределение электронной плотности. Вы можете видеть отдельные атомы и манипулировать ими. Один из самых популярных объектов для сканирующей туннельной спектроскопии — это графит. Мы знаем его атомную структуру. Она состоит из шестиугольных слоев. Мы это знаем из других экспериментальных методов. Говорят, что сканирующая туннельная микроскопия позволяет видеть отдельные атомы.
Эксперимент.
§1. Элементы теории туннельного эффекта
Рассмотрим
прохождение микрочастицей прямоугольного потенциального барьера высотой ![]() и шириной
и шириной ![]() (рис.1).
(рис.1).
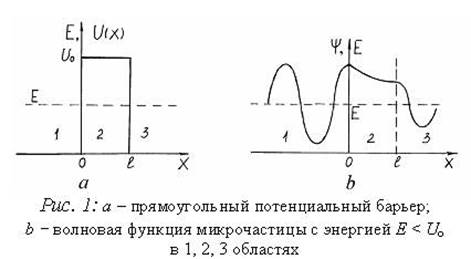
По классическим представлениям частица, движущаяся слева направо, пройдет
в область ![]() только в том случае, если ее
полная энергия
только в том случае, если ее
полная энергия ![]() больше высоты барьера
больше высоты барьера ![]() . Кинетическая энергия частицы в
областях 1, 2, 3 принимает соответственно значения
. Кинетическая энергия частицы в
областях 1, 2, 3 принимает соответственно значения ![]() .
Если энергия частицы меньше Uo (E < Uo), то на границе х
= 0, частица отражается от барьера и движется обратно (кинетическая энергия Ек
= Е - Uo не может иметь отрицательные
значения).
.
Если энергия частицы меньше Uo (E < Uo), то на границе х
= 0, частица отражается от барьера и движется обратно (кинетическая энергия Ек
= Е - Uo не может иметь отрицательные
значения).
Совершенно иная ситуация складывается для частиц, подчиняющихся квантовым закономерностям. Для них есть отличная от нуля вероятность отражения от барьера при энергии Е > Uo и отличная от нуля вероятность проникновения в область х > l через барьер при Е < Uo.
В чем же причина такого «абсурдного» поведения частицы с точки зрения «наблюдателя», живущего в макромире и наблюдающего движение макротел, подчиненное законам классической механики? Современная физика утверждает: в микромире частицы обладают свойствами и частицы, и волны (такое явление называют корпускулярно-волновым дуализмом).
Обсудим качественно движение микрочастиц в области потенциального
барьера. С этой целью обратимся к соотношению неопределенностей Гейзенберга: ![]() (1),
(1),
где Dх, Dрх - неопределенности координаты х и импульса Dрх,
h - постоянная Планка.
В областях 1 и 3
частица имеет вполне определенный импульс ![]() ,
но совершенно неопределенную координату
,
но совершенно неопределенную координату ![]() .
.
В области 2
координата частицы имеет неопределенность порядка ширины барьера ![]() , а значит, неопределенность
импульса не меньше
, а значит, неопределенность
импульса не меньше ![]() (2)
(2)
и
неопределенность кинетической энергии не меньше ![]() (3).
(3).
То есть в области барьера полную энергию частиц нельзя представить в виде суммы точно определенных кинетической и потенциальной энергий. В связи с имеющейся неопределенностью в значении кинетической энергии частиц в области 2, возможно либо ее отражение, либо прохождение в область 3.
Явление прохождения частиц с ![]() через
барьер получило название туннельного эффекта (туннелирования).
Проходя через барьер, частица не изменяет свою полную энергию, т.е., как бы
проходит через «туннель» в этом барьере.
через
барьер получило название туннельного эффекта (туннелирования).
Проходя через барьер, частица не изменяет свою полную энергию, т.е., как бы
проходит через «туннель» в этом барьере.
Оценка 1. Оценим ширину барьера высотой Uо = 5 эВ, через который возможно туннелирование электрона с энергией Е = 2 эВ.
Если
определить минимальную неопределенность импульса через превышение высоты
барьера над энергией частицы ![]() и
и ![]() , то из соотношения (1) следует,
что ширина барьера, доступная для туннелирования, равна
, то из соотношения (1) следует,
что ширина барьера, доступная для туннелирования, равна 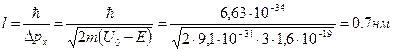
Строгое описание движения частиц в области барьера
можно получить, решив стационарное уравнение Шредингера, которое при ![]() имеет вид
имеет вид ![]() (4) в
областях 1 и 3,
(4) в
областях 1 и 3,
и ![]() (5) в области 2.
(5) в области 2.
Решения уравнений (4) и (5) могут быть записаны в виде:
область 1 ![]()
область 2 ![]() (6)
(6)
область 3 ![]()
Здесь ![]() ,
, ![]() ,
,
![]()
![]() .
.
Итак: ![]()
![]() -
для области 1,
-
для области 1,
![]() - для области 2,
- для области 2,
![]() - для области 3.
- для области 3.
Первые слагаемые первого и третьего уравнений (6) можно интерпретировать как плоские волны, распространяющиеся слева направо, а вторые как волны, отраженные в точках разрыва потенциальной функции Uо, то есть от «стенок» потенциального барьера. В связи с этим коэффициент В3 следует положить равным нулю, так как в области 3 нет физических причин для «отражения».
Решения (6) должны удовлетворять условиям непрерывности, конечности и иметь непрерывные производные:
![]() ,
, ![]() (7а)
(7а)
![]() ,
, ![]() (7б)
(7б)
Условия (7а и 7б) позволяют связать между собой
коэффициенты уравнений (6) и выразить их через А1.
Качественно вид волновых функций (6) показан на рис.1 б. В
областях 1 и 3 функции ![]() и
и ![]() описывают состояние частицы с
энергией Е и имеют одинаковую частоту, но отличаются амплитудой. Функция
описывают состояние частицы с
энергией Е и имеют одинаковую частоту, но отличаются амплитудой. Функция
![]() имеет вид затухающей функции.
имеет вид затухающей функции.
Отношение квадратов модулей амплитуд прошедшей и
падающей на барьер волны  определяет
вероятность прохождения (туннелирования) частицы через барьер и называется коэффициентом
прохождения или коэффициентом прозрачности.
определяет
вероятность прохождения (туннелирования) частицы через барьер и называется коэффициентом
прохождения или коэффициентом прозрачности.
Для
прямоугольного барьера можно показать из (6) и (7), что ![]() (8)
(8)
Оценка 2. Оценим коэффициент прозрачности для барьера, рассмотренного в оценке 1. То есть, рассмотрим туннелирование электрона с энергией 2 эВ через барьер шириной l = 0,7 нм и высотой Uо =5 эВ:
![]()
Коэффициент прозрачности рассматриваемого относительно широкого барьера мал, но при уменьшении ширины барьера в 5 раз (l = 1,4×10-10 м) проницаемость барьера составит уже весьма заметную величину:
![]()
Туннельный эффект лежит в основе многих явлений атомной и ядерной физики (например, a-распада, автоионизации атомов под действием электрического поля, термоядерных реакций), физики твердого тела (например, автоэлектронной эмиссии электронов из металла под действием электрического поля). Туннельный эффект является основой работы приборов современной микроэлектроники – диодов и транзисторов.
Оценка 3. В полях высокой напряженности электроны могут переходить из валентной зоны полупроводника в зону проводимости посредством туннелирования через запрещенную зону. Этот эффект называется эффектом Зиннера или электростатической ионизацией.

Энергетическая диаграмма собственного полупроводника,
помещенного в электрическое поле напряженностью ![]() ,
показана на рис.2.
,
показана на рис.2.
Электрон
из точки О валентной зоны (Еv) может
перейти в зону проводимости (Ес), туннелируя через
потенциальный барьер, энергия которого изменяется по закону ![]() , если отсчитывать ее от потолка
валентной зоны. Для барьера произвольной формы
, если отсчитывать ее от потолка
валентной зоны. Для барьера произвольной формы ![]() (рис.3)
коэффициент прозрачности определяется выражением
(рис.3)
коэффициент прозрачности определяется выражением 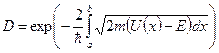 (9)
(9)
В рассматриваемом случае треугольного барьера при учете, что ![]() выражение (9) примет следующий вид
выражение (9) примет следующий вид
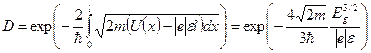 (10)
(10)
где ![]() - эффективная масса носителя
заряда.
- эффективная масса носителя
заряда.
Оценим
величину электрического поля ![]() и ширину
потенциального барьера l, при которых
вероятность туннелирования электрона из валентной зоны в зону проводимости
составляет D = 0,01. Положим ширину запрещенной
зоны
и ширину
потенциального барьера l, при которых
вероятность туннелирования электрона из валентной зоны в зону проводимости
составляет D = 0,01. Положим ширину запрещенной
зоны ![]() = 1 эВ, а массу
носителя
= 1 эВ, а массу
носителя![]() , тогда
, тогда
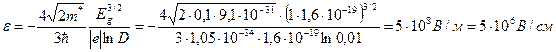
![]()
Экспериментальные данные для полупроводников с шириной запрещенной зоны около 1 эВ показывают, что эффект Зиннера действительно наблюдается в них при напряженностях поля 106 ¸107 В/см, которым соответствует ширина потенциального барьера 1,10 нм. Следовательно, полученная оценка является достоверной.
Выводы:
![]() - для области 2,
- для области 2,
![]() - для области 3.
- для области 3.
§2. Туннельный диод
Туннельным диодом называют полупроводниковый прибор, работа которого основана на квантовом эффекте туннелирования электронов через тонкий потенциальный барьер в области контакта двух полупроводников с различным типом проводимости. Впервые этот эффект на p-n – переходе был изучен японским ученым Есаки. За работы по развитию методов туннельной спектроскопии Есаки в 1973 году разделил Нобелевскую премию с Жевером и Джозефсоном (за работы по исследованию эффектов туннелирования в сверхпроводниках).
Изготавливают туннельные диоды из сильнолегированных полупроводников, у которых уровень Ферми располагается в зоне проводимости в полупроводнике n – типа и в валентной зоне в полупроводнике р – типа. Такие полупроводники называются вырожденными. Уровень Ферми–это уровень, соответствующий максимальной кинетической энергии электронов ЕF при температуре Т=0 К. Энергию, соответствующую этому уровню называют энергией Ферми. При абсолютном нуле температуры в полупроводнике все состояния с энергией Е £ ЕF заняты электронами, а состояния с Е > ЕF - свободны.

На рис.4а показана диаграмма p-n – перехода в вырожденных полупроводниках в состоянии термодинамического равновесия (внешнее электрическое поле отсутствует) при температурах вблизи абсолютного нуля.
Ширина области контакта l в вырожденном p-n – переходе настолько мала (l<10 нм), что возможно туннелирование носителей через переход. Уровень Ферми постоянен вдоль перехода. В области n–типа электроны заполняют зону проводимости вплоть до уровня Ферми, в то время как состояния выше уровня Ферми в области р–типа заняты дырками. Число туннельных переходов электронов слева направо и справа налево одинаково, и ток через переход отсутствует.
Равновесие можно нарушить, приложив к переходу напряжение смещения V. Если положительный полюс источника напряжения присоединен к материалу р–типа, а отрицательный к материалу n–типа, то такое включение диода называется прямым (положительным). При этом энергетические состояния в зоне проводимости смещаются вверх по отношению к энергетическим состояниям валентной зоны. Напротив состояний, занятых электронами в n–области, оказываются состояния, занятые дырками в р–области (рис.4б). Электроны из зоны проводимости n–области туннелируют через потенциальный барьер на свободные состояния (занятые дырками) в р–области.
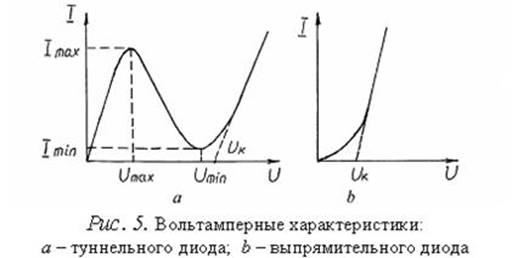
При увеличении напряжения ток через переход возрастает
(рис.5) и достигает максимума при напряжении Vmax,
при котором максимумы функций распределения электронов и дырок совпадают, т.е.
наибольшая плотность занятых состояний в n–области
соответствует максимальной плотности свободных состояний в р–области.
Анализ энергетических диаграмм показывает, что при почти одинаковых
концентрациях электронов и дырок ![]()
![]() (11),
где
(11),
где
Еm – энергия, соответствующая максимуму функции распределения электронов n (E).
Концентрацию электронов в n–области
можно рассчитать, пользуясь выражением ![]() ,
,
![]() (12) где
(12) где
m – эффективная масса электрона, ![]() – постоянная Планка.
– постоянная Планка.
При дальнейшем увеличении напряжения ток через переход уменьшается, и при совпадении границ зоны проводимости n-области и валентной зоны р–области туннельный ток практически прекращается, так как против энергетических состояний, занятых электронами, находятся запрещенные состояния. При V=Vmin через p-n–переход протекает обычный диодный ток p-n–перехода, смещенного в прямом направлении. С увеличением напряжения (V > Vmin) диодный ток резко возрастает. Как видно из рис.4а,
![]() (13)
(13)
При подаче на p-n–переход отрицательного смещения (рис.4г), через него протекает туннельный ток, обусловленный переходами электронов из р–области на пустые состояния n–области.
Как показывает теоретический анализ, энергия Еm, соответствующая максимуму функции распределения
электронов в зоне проводимости, может быть найдена из выражения ![]() (14), где
(14), где
k – постоянная Больцмана,
Т – температура;
а энергетическое
расстояние между дном зоны проводимости и уровнем Ферми можно рассчитать по
формуле ![]()
![]() (15)
(15)
Наличие в вольтамперной характеристике туннельного диода участка с отрицательным дифференциальным сопротивлением (rg=dV/dI, ток уменьшается с ростом напряжения) позволяет успешно использовать его для генерации и детектирования сверхвысокочастотных колебаний вплоть до частот 1011 Гц в различных устройствах приемопередающей аппаратуры и радиолокационных станциях. Высокая скорость переключения (около 10-10 с) дает возможность широко использовать туннельные диоды в импульсных схемах ЭВМ и различных устройствах автоматики.
Работая на основных носителях, туннельные диоды значительно менее чувствительны к ионизирующему излучению по сравнению с обычными полупроводниковыми приборами. Это свойство крайне важно при проектировании аппаратуры, работающей в условиях повышенного фона ионизирующего излучения (бортовая аппаратура спутников, приборы автоматики ядерной энергетики и др.).
В работе исследуются вольтамперная характеристика германиевого туннельного диода и для сопоставления с ней вольтамперная характеристика выпрямительного плоскостного диода.
Схема установки для снятия вольтамперной характеристики туннельного диода представлена на рис.6а.
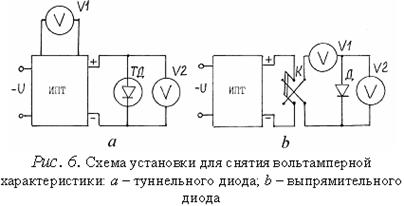
Туннельный диод (ТД) подключен в прямом направлении к регулируемому источнику постоянного тока (ИПТ) с низким внутренним сопротивлением. Сопротивление источника питания должно быть меньше отрицательного сопротивления диода на падающем участке вольтамперной характеристики. Ток диода контролируется цифровым вольтметром (V1), включенным в выходную цепь источника питания, а напряжение на диоде измеряется цифровым вольтметром (V2), включенным параллельно диоду. Схема для снятия вольтамперной характеристики выпрямительного диода показана на рис.6 б.
Напряжение от регулируемого источника постоянного тока (ИПТ) подается на диод (Д) через ключ (К), позволяющий изменить полярность включения диода. Ток, протекающий через диод, и напряжение на нем контролируются цифровыми вольтметрами (V1) и (V2).
Выполнение работы и обработка результатов измерений
Пусть мы включили установку для снятия вольтамперной характеристики туннельного диода: изменяя напряжение через 10 мВ в диапазоне от 0 до Vmax= 50 мВ.
По формуле (11) определим![]() .
.
Концентрация ионов в ![]() области по
формуле (12) равна
области по
формуле (12) равна 
![]() .
.
Энергетическое расстояние между дном зоны проводимости и уровнем Ферми по
формуле (15) равна ![]() .
.
По формуле (13) определим ![]()
Построим для туннельного диода эскиз графика зависимости тока от напряжения.
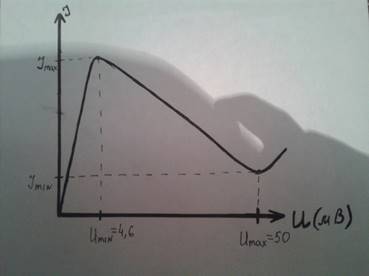
Изобразим с соблюдением масштаба по энергии энергетическую диаграмму p-n–перехода туннельного диода (ширина запрещенной зоны
германия ![]() , ширина p-n–перехода
l = 2,0 нм, площадь перехода S = 10-7
м2.).
, ширина p-n–перехода
l = 2,0 нм, площадь перехода S = 10-7
м2.).
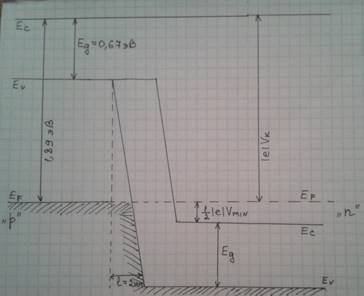
Выводы:
Ширина запрещенной зоны германия при комнатной температуре ![]() .
.
Ширина p-n–перехода туннельного диода l = 2,0 нм.
Характерные точки вольтамперной характеристики туннельного диода: ![]() ,
, ![]()
![]()
![]()
Энергетическое расстояние между уровнем Ферми и энергией, соответствующей
максимуму функции распределения электронов ![]()
Энергетическое расстояние между уровнем Ферми и дном зоны проводимости
![]()
Концентрация носителей в зонах вырожденного p-n–перехода
![]() .
.
Заключение.
В этой работе я лишь приподняла завесу над исследованием физики сверхпроводимости. Эту тему можно было бы изучить намного глубже, но к большому сожалению подобное изучение данной темы выходит за рамки данной работы. Остается еще много вопросов, на которые пока не получены ответы.
В 1974 году Л. Купер в своей Нобелевской лекции привел следующие высказывания выдающегося французского математика Анри Пуанкаре: «Ученый должен систематизировать факты. Наука состоит из них подобно тому, как здание состоит из кирпичей. Однако простое нагромождение фактов похоже на науку не более, чем груда камней на дом». От себя Купер добавил: «Из обычных камней можно построить и скромный дом, и великолепный замок. С утилитарной точки зрения и то, и другое служит для ограничения некоторой части пространства с целью предохранить её от дождя и холода. Разница состоит в претензиях и средствах строителей и в искусстве, с которым они воплощают свой замысел. Теория, оперирующая стандартными понятиями, также может быть полезна при решении многих скромных задач. Однако когда мы вступаем в сферу общих концепций и идей, перед нашим взором открывается нечто подобное архитектурным шедеврам с колоннами умопомрачительной высоты и арками дерзкой и почти невероятной ширины. Они сводят во едино данные о магнитном моменте электрона и о явлениях на стыке двух различных металлов при абсолютном нуле, они покрывают расстояние от свойств вещества при экстремально низких температурах до его поведения в недрах звезд, от четности операторов относительно движения времени до особенностей коэффициентов затухания вблизи критической температуры. Говоря об этом, я хотел бы убедить моих коллег – теоретиков, а также и самого себя в том, что в конечном счете наша «голубая мечта» должна состоять в построении не только практически полезного, но и эстетически прекрасного здания науки».
От себя я могу только добавить, что все мы живем в этом городе науки, где есть дворцы, есть и хижины. Кто приносит на строительство этих сооружений маленький кирпич, кто стесывает резкие углы глыбы, внесенных гигантами. Я хочу пожелать будущим жителям этого города любить его. В нем не только необычайной красоты проспекты и улицы, но и прекрасные закоулки, надо только учиться видеть неповторимую красоту результатов деятельности человеческого разума.
Литература:
1) В.М. Свистунов, В.Н. Леонова «Туннелирование в сврхпроводниках под давлением», статья/ УДК-539.292/ г. Харьков – НТУ «Харьковский политехнический университет.
2) Н.Б. Делоне «Туннельный эффект», статья/ г. Долгопрудный, Московская область –Московский физико-технический институт, 2000.
3) Г.В. Жарков «Туннельный эффект Джозефсона в сверхпроводниках», статья/ 537.312.62/ Физический институт им. П. Н. Лебедева АН СССР – 1996., том 88, вып. 3.
4) В.В.Курин «Физика сверхпроводников. Вводный курс», уч. пособие для студентов РФ и ВШОПФ ННГУ им. Лобачевского/ Институт физики микроструктур/ г. Нижний Новгород, 2004.
5) Я.В.Фоминов, Н.М.Щелкачёв «Эффект Джозефсона», учебно-методическое пособие/ УДК538.945/ Московский физико-технический институт, кафедра теоретической физики - М.: МФТИ, 2010.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.