Учебно-исследовательская работа «Необыкновенные способы сложения и вычитания обыкновенных дробей»

Управление по образованию

Молодечненского райисполкома

 

Государственное учреждение образования

«Городиловская средняя школа Молодечненского района»

 

 

Учебно-исследовательская работа

 

«Необыкновенные способы сложения и вычитания обыкновенных дробей»

 

 

 

 

 

 

Выполнили работу:

Войтехович Виктория,

учащаяся 5 класса,

Иванчик Анастасия,

учащаяся 5 класса,

Лазарь Кирилл

учащийся 5 класса,

Радиончик Иван,

учащийся 5 класса

 

Руководитель:

Михновец Е.И.,

учитель математики

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2021

СОДЕРЖАНИЕ

СОДЕРЖАНИЕ …….................................................................................................2

ВВЕДЕНИЕ ………………………………………………………………………….3

СНОВНАЯ ЧАСТЬ ………………………….……………………………….……...5

1. НЕСТАНДАРТНЫЕ СПОСОБЫ СЛОЖЕНИЯ ДРОБЕЙ ………………..……5

1.1. Метод бабочки ……...……………………………………………………..……5

1.2. Сложение и вычитание обыкновенных дробей.Решаем быстро и красиво ……………….……………………………………..………...…...………………….6

2. АНАЛИЗ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ ……...……...……….…………8

ЗАКЛЮЧЕНИЕ ………………….……………………………….…….……………9

ЛИТЕРАТУРА……………………………………………………………...……..  10

ПРИЛОЖЕНИЕ 1 …………………………..……………………….…………….11

ПРИЛОЖЕНИЕ 2 …………………………………………………….…………..12

ПРИЛОЖЕНИЕ 3 ………………………………………………..……………….13

ПРИЛОЖЕНИЕ 3 ………………………………………………..………….……14

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

\

 

 

 

 

 

 

 

 

 

 

ВВЕДЕНИЕ

С обыкновенными дробями мы познакомились ещё в начальной школе. Интересным и необычным было всё: начиная с их непривычной записи и заканчивая решением простейших задач на дроби. Нам казалось, что обыкновенные дроби – это легко и просто. В пятомклассе продолжили изучать тему «Обыкновенные дроби». При изучении данной темы мы по-новому раскрыли для себя удивительный мир обыкновенных дробей, узнали много новых фактов из   истории их возникновения и развития. 

На уроках математики и в повседневной жизни всё время приходится сталкиваться с дробями. Оказалось, что действия с дробями довольно сложные и требуют набора определённых знаний и навыков, которые все вместе дают возможность применять в реальной жизни полученные в школе знания.  Сдробями математика оказалась гораздо сложнее, чем мы думали, но в тоже время захватывающей и увлекательной.

Актуальность исследования: Натуральные числа встречаются в математике и тем более при решении практических задач редко.Магазин, аптека, банк, ателье, стройка, ферма, сад и огород  всюду встречаемся с дробными значениями величин, поэтому так необходимо владеть всеми действиями с дробями, включая сложение и вычитание дробей.

Объектом исследования является: алгоритм сложение и вычитания дробей

Предметом исследования выступает процесс вычисления.

Методы исследования:

·        изучение литературы и Интернет-ресурсов по данной теме;

·        анализ информации с помощью сравнения, обобщения, аналогии;

·        личные наблюдения, опросы;

·        обработка результатов опроса.

Цель: изучить нестандартные приемы вычислений и экспериментальным путем выявить причину отказа от использования этих способов при обучении математике современных школьников.

В соответствии с поставленной целью решались следующие задачи:

·        изучить необходимую литературу, Интернет-ресурсы;

·        описать классический способ вычисления суммы и разности обыкновенных дробей и выявить трудности в их использовании;

·        рассмотреть некоторые нестандартные приемы вычисления суммы и разности обыкновенных дробей и на конкретных примерах показать преимущества их использования.

·        предложить свой способ нахождения суммы и разности обыкновенных дробей;

·        провести анкетирование;

·        обобщить собранные материалы.

Гипотеза исследования: в результате этой работы нам удастся найти свой оригинальный способ сложения и вычитания обыкновенных дробей, который будет отличаться от известных ранее.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОСНОВНАЯ ЧАСТЬ

Глава 1. Нестандартные способы сложения дробей

В этом учебном году мы познакомились с основными свойствами дробей, научились выполнять все действия с ними (складывать, вычитать, умножать и делить), решать основные типы задач на дроби.     

Самым сложным для нас было освоить правило сложения и вычитания дробей. Для многих наших одноклассников сложной оказалась тема сложения и вычитания дробей с разными знаменателями.  Первые неудачи и разочарования. Возник вопрос, а может есть другие, балле простые, способы сложения дробей? Это заставило нас заняться изучением данного вопроса. 

Глава 1.1. Метод бабочки.

При работе с Интернет-ресурсами мы сразу же нашли интересную публикацию учителя математики Дмитрия Давидюка, который опубликовал свой способ, помогающий легко складывать дроби с разными знаменателями, с красивым названием «Метод бабочки». Ролик набрал много миллионов просмотров.

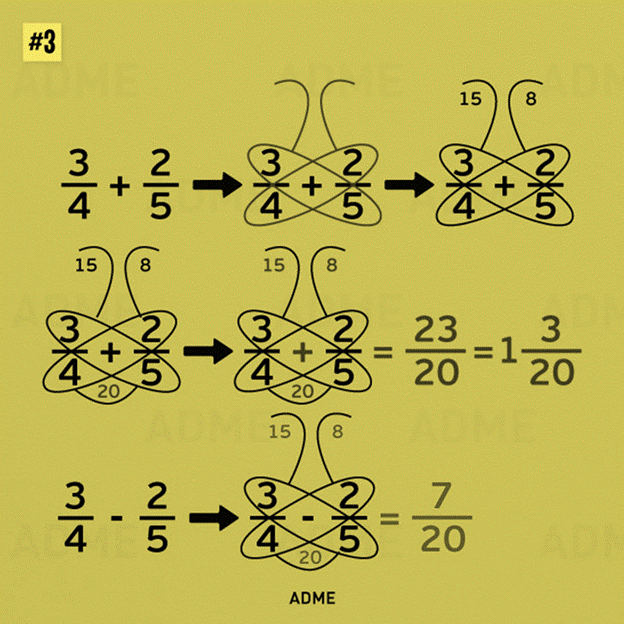
Суть «Метода бабочки» заключается в том, что при сложении дробей нужно умножить числитель первой дроби на знаменатель второй, а затем числитель второй на знаменатель первой. Сумма двух получившихся чисел будет числителем дроби в ответе, а ее знаменателем — результат умножения знаменателей складываемых дробей.(Приложение 1)

Тысячи восторженных комментариев. «Если бы так прекрасно учителя объясняли в школе, то я любила бы математику», — написала одна из пользовательниц. Первое впечатление действительно «гениально». Возник вопрос почему в школе не используют этот метод?

Способ предложенный в школьном учебнике универсальный. При детальном рассмотрении «Метода бабочки» сразу становиться понятно, что данный способ прекрасно работает лишь когда знаменатели однозначные числа и по существу, повторяет правило сложения дробей для случая, когда знаменатели взаимно простые числа.       Давайте попробуем сложить дроби «Методом бабочки» если знаменателидвузначные или трёхзначныечисла.

Учитель математики выслушав нас, предложи сложить «методом бабочки»   +   и    +   (случай, когда знаменатели двузначные или трёхзначные числа).

 Решение.

1)  +   =  =  =   =  =   =  (*);

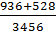2)   +  =  =  =   = =  =  (**)

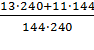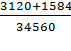Нам сразу стало понятно, что данный способ прекрасно работает лишь тогда, когда знаменатели однозначные числа и по существу, повторяет правило сложения дробей для случая, когда знаменатели взаимно простые числа.

Очевидно, в случае, когда знаменатели многозначные числа, данный метод требует громоздких письменные вычислений в столбик при решении не с примеров на сложение и вычитание дробей.

Делаем выводы:очевидно«метод бабочки» работает только в случае, когда знаменатели однозначные числа и по существу является применением правила сложения дробей со взаимно простыми знаменателями, простейшие примеры из учебника, в которых знаменатели двузначные числа, а тем более трёхзначные в ходе решения требуют громоздких вычислений, что не является рациональным; сложение в цепочку более двух слагаемых невозможно.

Глава 1.2. Сложение и вычитание обыкновенных дробей. Решаем быстро и красиво

При решении поставленных нами задач, мы столкнулись с необходимостью расширить знания признаков делимости натуральных чисел.

Знание признаков деления натуральных чисел необходимо при решении многих арифметических задач, в частности при выполнении действий с обыкновенными дробями.

Из школьного курса математики каждому из нас хорошо известны признаки делимости чисел на 2, на 3, на 4, на 5, на 9 и 10. Очевидно, что признаки делимости на 6, на 8, на 12, на 14, на 15, на 25 следуют из перечисленных выше. Например, если число a делится на число 12 тогда и только тогда, когда число a делится на 3 и на 5 одновременно.(Приложение 2)

Самая сложная часть в алгоритме сложения дробей – найти наименьший общий знаменатель. В ходе исследований мы заметили следующую закономерность. Допустим надо привести дроби      и    к наименьшему общему знаменателю, между знаменателями 16 и 36 есть связь - их связывает общий делитель 4 (16:4 4 и 36:4 9).

Мы заметили, что, если взять результат деления первого знаменателя в качестве дополнительного множителя ко второй дроби  и, соответственно, второго знаменателя в качестве дополнительного множителя к первой дроби, мы получим наименьший общий знаменатель.

Приведем примеры:

1.       и ; и ;       и  (4:2=2 и 6:2=3, связаны делителем 2)

2.       и  ;   и ;        и     (45:15=3 и 60:15=4связаны делителем 15)

3.       и  ;    и ;       и  (21:7=3 и 35:7=5, связаны делителем 7)

 

Как видно, приводить к общему знаменателю с помощью общего делителя очень просто.   Дроби с общим знаменателем  слаживать и вычитать  умеют все.

Примеры.

1.   +   = +   =    +   =

        

2.    +   = +   =    +   =  = (   =  =  ) 

 

3.  +   = +   =    +   = (   =  =  ) 

 

4.    +  = +   =  +  = (   =  =  ).

Разберем решение примеров (*) и (**), предложенных на странице 4, с помощь признаков деления:

1.  +  = +  =+ = ( );

 

2.    +  = +  =+  = =  ( )

Преимущество нашего способа очевидно. Учитель математики согласился с нами. Большинство наших одноклассников при сложении и вычитании дробей используют полученный нами алгоритм.

Найденный нами способ сложения и вычитания дробей с помощью признаков деления чисел гораздо проще, принятого через нахождения НОК. Почему его нет в школьных учебниках? У этого способа есть один существенный недостаток: сложение в цепочку более двух слагаемых невозможно, а при решении примеров сложной конструкции этот момент играет важную роль.

Делаем выводы:используя признаки деления натуральных чисел находить общий знаменатель двух дробей гораздо проще, чем через НОК, что значительно упрощает алгоритм сложения дробей с разными знаменателями, но сложение в цепочку более двух слагаемых невозможно.

 

ГЛАВА 2. АНАЛИЗ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ

Всем понятно, что пока мы учимся в школе, то   нам необходимы знания дробей и действий над ними. А нужны ли знания дробей в повседневной жизни нашим родителям, бабушкам и дедушкам, применяют ли они эти знания при решении практических задач.  Мы провели опрос средиродителей своего класса. Результаты приведены в диаграмме 2.1. (Приложение 3)

Большинство родителей подтвердили, что дроби в нашей жизни встречаются практически на каждом шагу.Мама использует дроби для расчета продуктов при приготовлении блюд, отец при изготовлении строительных растворов и смесей, провизоры в аптеках при изготовлении лекарств, садовод использует при приготовлении удобрений и защиты растений, учителя математики и музыки используют в своей работе.

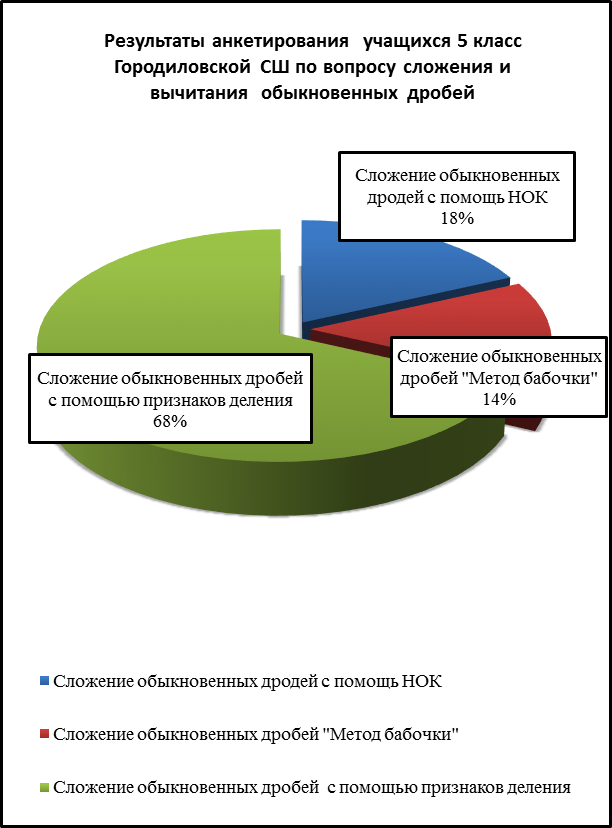
С результатами наших исследований мы прежде всего познакомили своих одноклассников. Нам удалось убедить их в том, что предложенный нами способ простой и эффективный. Как показало анкетирование, большинство из них при сложении дробей используют именно его. Результатыанкетирования  учеников 5 класса Городиловской СШ  приведены в диаграмме 2.2. (Приложение 4)

Делаем выводы:родители и ученики убеждены в необходимости знаний обыкновенных дробей, их свойств не только для успешного   изучения предмета математика, но и в повседневной жизни при решении практика ориентированных задач.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗАКЛЮЧЕНИЕ

Обыкновенные дроби – это отдельный раздел в математике со своими интересными определениями, свойствами, правилами. Действия с дробями важно не только знать, но по-настоящему владеть ими.

Результаты анкетирования в 5 классе родителей и учеников показали, что дроби присутствуют вокруг нас. А значит, выбранная нами тема не только важна при изучении математики в школе, но и будет актуальна при различных расчетах практических задач в реальной жизни.

На уроках математики и факультативах мы познакомили своих одноклассников с результатами нашего исследования. Большинству из них материал показался интересным, многие стали его использовать при вычислениях.

Надеемся, что результаты нашей работы будут использоваться не только нашими одноклассниками, но и учителями нашей школы. Свои результаты мы постараемся распространить среди школьников и с помощью социальных сетей.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЛИТЕРАТУРА

1.     Большая энциклопедия школьника. Москва «Махаон» 2006г.

2.     2. Ожегов С.И., Шведова Н.Ю. Толковый словарь русского языка С. И. Ожегов, Н. Ю. Шведова. – М. : Азбуковник, 1999. — 944 с.

3.     Энциклопедия для детей. Всё обо всём – М.: 1996 – 446 с.

4.     https://umath.ru/theory/priznaki-delimosti-chisel/

5.     https://www.facebook.com/watch/?v=444990942702045

6.     https://www.adme.ru/zhizn-nauka/10-prostyh-matematicheskih-tryukov-837610/

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ 1.

«Метод бабочки» для сложения и вычитания дробей

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ 2.

Таблица признаков делимости чисел

 

Число n	Число a делится на число n тогда и только тогда, когда
2	Последняя цифра числа a делится на 2
3	Сумма цифр числа a делится на 3
4	Число, составленное из двух последних цифр числа a, делится на 4
5	Число a оканчивается цифрой 0 или 5
6	Число a делится на 2 и на 3
7	Знакочередующаяся сумма трёхзначных граней* числа a делится на 7
8	Число, составленное из трёх последних цифр числа a, делится на 8
9	Сумма цифр числа a делится на 9
10	Число a оканчивается цифрой 0
11	Знакочередующаяся сумма трёхзначных граней* a делится на 11
12	Число a делится на 3 и на 4
13	Знакочередующаяся сумма трёхзначных граней* a делится на 13
14	Число a делится на 2 и на 7
15	Число a делится на 3 и на 5
13	Знакочередующаяся сумма трёхзначных граней* a делится на 13
25	Число, составленное из двух последних цифр числа a, делится на 25

 

*Грани числа – числа, полученные при разбиении исходного числа на двузначные или трёхзначные числа, взятые справа налево. Например, разбиение числа 1234567 на двузначные грани выглядит так: 1|23|45|67, а на трёхзначные так: 1|234|567.

        

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ 3.

Диаграмма 2.1

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ 4.

Диаграмма 2.2

 

 

Скачано с www.znanio.ru