Учебно-методический материал по информатике и ИКТ "Алгебра логики" теория, 1 часть, для 7-11 классов

УЧЕБНО-МЕТОДИЧЕСКИЙ МАТЕРИАЛ ПО ИНФОРМАТИКЕ И ИКТ

«АЛГЕБРА ЛОГИКИ»

Теория

1 часть

СОДЕРЖАНИЕ:

1. История развития логики                                                                - 3

2. Основные формы мышления                                                           - 5

3. Логические операции

4. Порядок составления

таблиц истинности для логических выражений             - 11   -

5. Законы алгебры логики

Правила преобразования логических выражений          - 12

1. История развития логики

Логика, созданная как наука Аристотелем (384–322 г. до н.э.), на протяжении столетий использовалась для развития многих областей знания, включая теологию, философию, математику.

Она – тот фундамент, на котором построено все здание математики. По сути,  логика — это наука о рассуждениях, которая позволяет определить истинность или ложность того или иного математического утверждения, исходя из совокупности первичных предположений, называемых аксиомами. Логика применяется также в информатике для построения компьютерных программ и доказательства их корректности. Понятия, методы и средства логики лежат в основе современных информационных технологий. Одна из основных целей этой работы — изложить основы математической логики, показать, как она используется в информатике, и разработать методы анализа и доказательства математических утверждений.

Вначале логика возникла и развивалась в недрах философии как единой науки, объединявшей всю совокупность представлений людей об окружающем мире и самом человеке, его мышлении. При этом первоначально законы и формы правильного мышления изучались в границах ораторского искусства, как одного из средств воздействия на умы людей, убеждения их в целесообразности определенного поведения.

I этап – формальная логика.

Основатель – древнегреческий философ Аристотель (384-322 гг. до н.э.), первым систематизировал формы и правила мышления, сформулировал основные законы мышления, ввел основные формы абстрактного мышления, разработал теорию умозаключений и доказательств. Аристотель приехал в Афины и поступил в школу - академию Платона, где пробыл 20 лет, сначала в качестве ученика, а затем в качестве учителя. Аристотель часто спорил со своим великим учителем, отстаивая свои философские идеи. Аристотель на всю свою жизнь сохранил уважение к своему Великому Учителю и ушел из академии только после его смерти. В 335 г. до н.э. в предместье Афин Аристотель создал свою школу, которую назвал лицеем. Занимаясь преподавательской деятельностью, Аристотель не прерывал связи с Александром Македонским. В своих письмах царю, он предостерегал его от упоения властью, призывал ценить друзей и карать льстецов и наушников. Аристотель создавал логику как науку о доказательстве истины. Он подошел вплотную к теории доказательств. Но решить эту задачу даже очень гениальному человеку было не под силу. Потребовались тысячелетия упорного труда до получения результатов.Античную логику, основанную Аристотелем, принято называть формальной логикой. Формальная логика связана с анализом обычных рассуждений, выражаемых разговорным языком.

II этап – математическая логика

 Основатель – немецкий ученый философ и математик Г.В.Лейбниц (1646-1716), высказал  идею о возможности математизации логики. Он пытался создать универсальный язык, с помощью которого разрешались бы споры между людьми, каждому понятию и суждению можно было бы дать числовую характеристику и установить такие правила  оперирования с этими числами, которые позволили бы сразу определить, истинно данное суждение или ложно. Воспитанию и образованию детей семье уделяли большое внимание. В пятнадцать лет Лейбниц поступил на юридический факультет Лейпцигского университета, а в 20 лет защитил докторскую диссертацию. Затем последовала вынужденная служба у коронованных особ. С 1668 года он работает в качестве дипломата, юриста, историографа. С 1676 г. – занимает должность заведующего придворной библиотекой при Брауншвейг-Люксембурском герцовством дворе. Всю жизнь его окружали недоверие и зависть. Их пренебрежение особенно усилилось в последние годы жизни. Но время подтвердило его гениальность, сохранив для потомков его имя и дела. Огромный титанический труд (около 75000 его работ хранятся в Ганноверском архиве) позволил ученому создать философскую систему, обогнав свое время на несколько столетий. Особый научный прорыв он совершил на стыке логики, математики, философии. Лейбниц был одним из первых, который всерьез интересовался двоичной системой счисления, в которой для счета достаточно двух цифр 0 и 1.

Лейбниц взглянул на логику Аристотеля через призму математики:

• все известные понятия сводились к сочетанию простых понятий;
• разработал идею логического счисления, то есть сформулировал правила действия с символами;
• простые рассуждения обозначались символами, сложные элементы логических высказываний обозначались формулами, а суждения – уравнениями;
• в результате удалось заменить содержательные высказывания формальными буквами, перейти к доказательству с помощью карандаша и бумаги.

Будущую теорию (которую он так и не завершил) он называет «всеобщая характеристика». Она включала все логические операции, свойства которых он ясно представлял

III этап – математическая логика (булева алгебра).

Основатель – английский математик Джордж Буль (1815-1864), перенес на логику законы и правила алгебраических действий, ввел логические операции, предложил способ записи высказываний в символической форме. Он автор известных произведений “Математический анализ логики” (1847) и “Исследование законов мысли” (1857) родился в городе Линкольне (Англия) в семье мелкого торговца. Материальное положение родителей было трудным, платить за обучение сына было невозможно, прошлось ограничиться начальными классами для детей бедняков. Джордж изо всех сил стремился получить образование. Он самостоятельно овладел латынью и греческим. Страсть к науке делала его невосприимчивым к пренебрежительным взглядам. В 1844 году он получает золотую медаль за работу по математическому анализу.

Оригинальные идеи Буля по достоинству оценены математиком Кембриджского университета А. Де Морганом и Д.Грегори. Благодаря их поддержке, не имея высшего образования, ни степени, в 1849 году он стал профессором математики католического колледжа в ирландском городе Корк, где провел последние пятнадцать лет своей жизни.

Основное произведение Д.Буля “Исследование законов мысли”. В этой книге представлена алгебраическая система, которую называют алгеброй высказывания.

Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной технике

2. Основные формы мышления

Логические представления - описание исследуемой сис­темы, процесса, явления в виде совокупности сложных высказываний, составленных из простых (элементарных) высказываний и логических связок между ними. Логические представления и их составляющие характеризуются опре­деленными свойствами и набором допустимых преобразо­ваний над ними (операций, правил вывода и т.п.), реализую­щих разработанные в формальной (математической) логике правильные методы рассуждений — законы логики.

 Алгебра — это раздел математики, исследующий операции, аналогичные сложению, умножению, вычитанию и делению, выполняемые не только над числами, но и над другими математическими объектами, например, многочленами, векторами, матрицами, операторами и т.д., над объектами самой различной природы. Возникла алгебра в связи с поисками общих приемов решения однотипных арифметических задач. В основе найденных алгеброй общих приемов лежат действия над величинами (составление и решение уравнений), выраженных буквами, независимо от их конкретного числового значения. 

В русском языке слово «умозаключение» используется в двух значениях: для обозначения процесса рассуждения, размышления, приводящего к некоторому выводу, и для обозначения результата этого процесса.

Ещё в древности было известно рассуждение, ставшее классическим образцом верного логического умозаключения:

Все люди смертны.

Сократ  человек.

Сократ смертен.

   Основными элементами математической логики являются высказывания или логические выражения. 

   Об объектах можно судить верно, или неверно, то есть высказывание может быть истинным или ложным. Истинным будет высказывание, в котором связь понятий правильно отражает свойства и отношения реальных вещей. 

   Пример: 

• Город Вашингтон – столица США (истинное);

• Число 2 является делителем числа 7 (ложное). 

   Высказывания могут быть представлены не только с помощью естественных языков, но и с помощью формальных языков (математических, химических и прочих знаков). 

Одно и то же высказывание разными людьми может восприниматься как истинное или ложное в зависимости от их взглядов, жизненного опыта, особенностей национальной культуры, воспитания, образования и т.д.

   Пример: 

• 5х5=25 (истинное); 

• Н+О=Н2О (ложное).

      Не все выражения являются высказываниями. 

   Пример: На улице идет дождь. Данное выражение не является высказыванием, так как в данном выражении не определены название города и улицы, не указано время. Поэтому нельзя установить истинность данного выражения. 

Примеры высказываний:

•         Земля – планета Солнечной системы (истинное высказывание).

•         3 + 6 > 10 (ложное высказывание).

•         Площадь прямоугольного треугольника равна произведению катетов (ложное высказывание).

•         Площадь прямоугольного треугольника равна половине произведения катетов (истинное высказывание).

•         Если на улице дождь, то асфальт – мокрый (истинное высказывание).

•         Свободу и комфорт человеку дают деньги (истинное или ложное высказывание, субъективно).

•         Солнце светит для всех  (истинное высказывание).

•         Все ученики любят информатику (ложное высказывание).

•         Некоторые ученики любят информатику (истинное высказывание)

•         Ты любишь информатику? (не высказывание, т.к. предложение не повествовательное).

•         Посмотри в окно (не высказывание).

•         Х*Х<0 (ложное высказывание, т.к. х*х всегда неотрицательно).

•         2*Х -5>0 (не высказывание, так как результат зависит от Х, значение которого неизвестно).

   Высказывание не может быть выражено повелительным или вопросительным предложением, так как оценка их истинности или ложности невозможна. Также, любое определение не может быть высказыванием, так как определения не могут быть истинными или ложными. Они фиксируют принятое использование терминов. 

   Высказывания могут быть простыми и сложными.

Например:

Квадрат – это ромб.

Звезды видны на небе только ночью.

Наступила зима.

Учебный год начинается 1 января.

Например, составное высказывание «Лил дождь, и дул холодный ветер» состоит из двух простых высказываний: «Лил дождь», «дул холодный ветер», соединенных союзом «и».

Истинность или ложность составных высказываний вычисляется с помощью использования алгебры высказываний.

 Например, составное высказывание «Принтер является устройством печати, а процессор является устройством вывода информации» является ложным, т.к. одно из простых высказываний, входящих в него является истинным, а другое – ложным.

   Простые логические высказывания обозначают заглавными латинскими буквами. значениями  логических высказываний могут быть только 0 (ложь) или 1 (истина).

Например:

A = Все мальчики – хулиганы. = 0 – ложное высказывание

B = В школе дети изучают информатику. = 1 – истинное высказывание

В алгебре логики над высказываниями можно производить определенные логические операции, в результате которых получают новые составные высказывания. Составное высказывание можно представить в виде формулы, в которую входят логические выражение, обозначающие высказывания, и знаки логических операций.

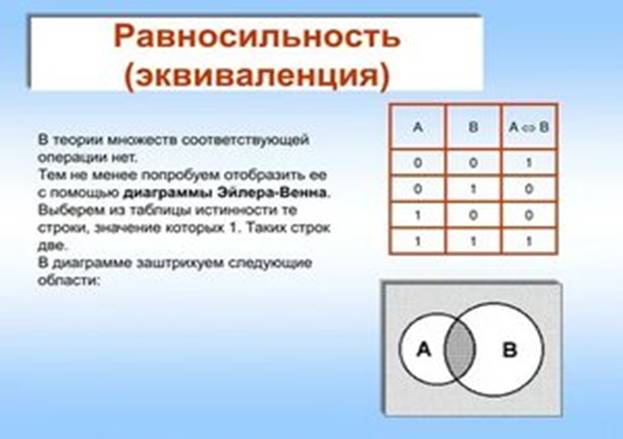
3. Логические операции

Порядок выполнения логических операций

1.      Операции в скобках

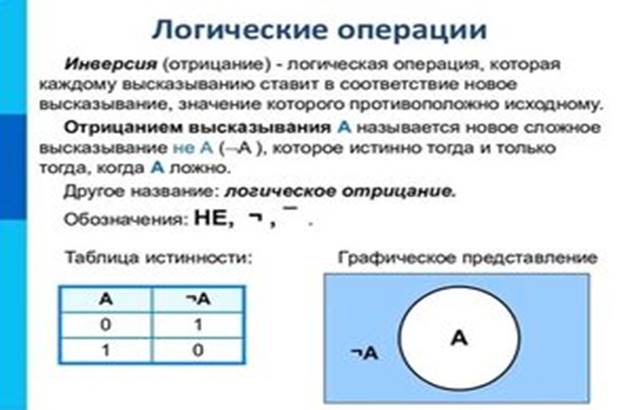
2.      Отрицание

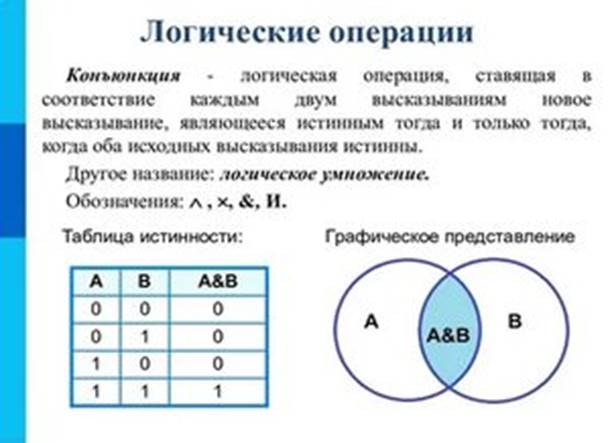
3.      Конъюнкция (логическое умножение)

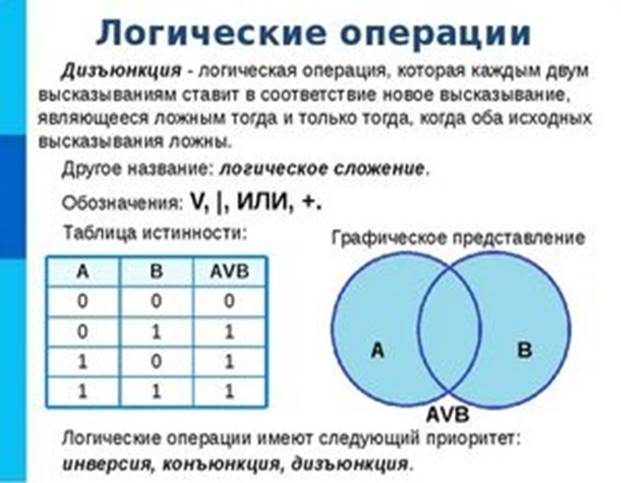
4.      Дизъюнкция (логическое сложение)

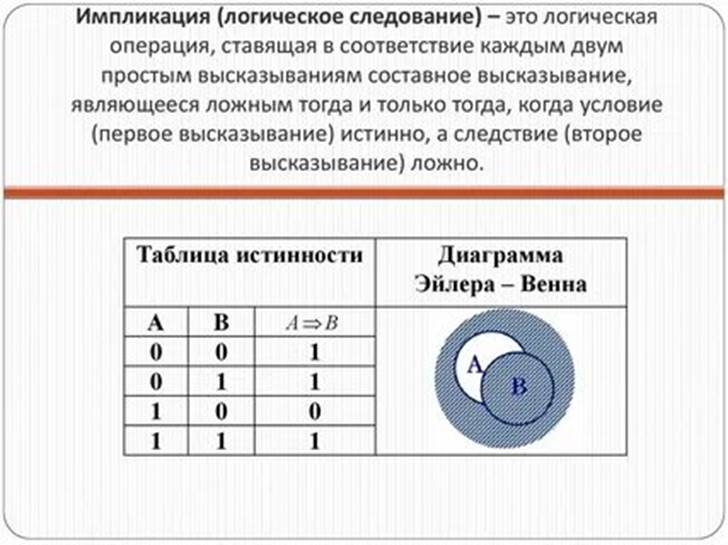
5.      Импликация

6.      Эквивалентность

7.       

Для изменения указанного порядка выполнения логических операций используются скобки.

4. Порядок составления таблиц истинности для логических выражений.

Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.

Количество строк (q) в таблице истинности можно вычислить по формуле

q = 2ⁿ

где n – количество логических выражений.

Количество столбцов в таблице истинности равно количеству логических выражений плюс количество логических операций в сложном логическом выражении.

Таблицу истинности необходимо заполнить по столбцам, выполняя логические операции в необходимой последовательности.

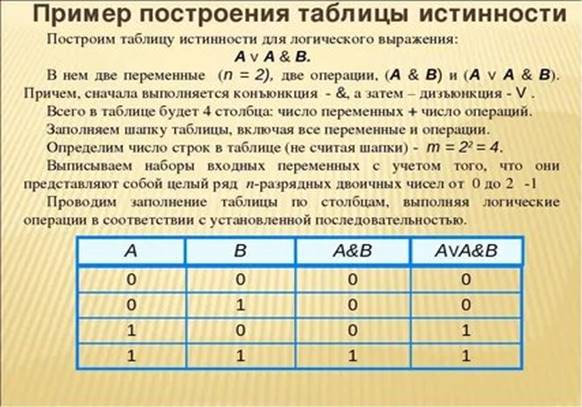
Алгоритм построения таблиц истинности:

1.     Определить количество строк в таблице истинности.

Количество строк = 2ⁿ, где n – количество логических переменных.

2.     Определить количество столбцов в таблице истинности, равное количеству логических переменных плюс количество логических операций.

3.     Построить таблицу истинности с указанным количеством строк и столбцов.

4.     Ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов.

5.     Заполнить столбцы входных переменных наборами значений.

6.     Заполнить таблицу истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.

5. Законы алгебры логики. Правила преобразования логических выражений

Законы логики отражают наиболее важные закономерности логического мышления. В алгебре логики законы логики записываются в виде формул, которые позволяют проводить преобразования логических выражений. Применение законов логики позволяет сокращать количество переменных в логических выражениях.

1.     Закон тождества:        А = А

Всякое понятие и суждение тождественно самому себе.

2.     Закон непротиворечия  или 

Не могут быть одновременно истинными суждение и его отрицание

3.     Закон исключенного третьего:

Высказывание может быть либо истинным, либо ложным, третьего не дано.

4.     Закон двойного отрицания:

Если отрицать дважды некоторое высказывание, то в результате получится исходное высказывание.

5.     Переместительный закон (закон коммутативности):

A v B = B v A           A & B = B & A

При операциях логического умножения или сложения можно менять местами логические переменные.

В математике: ab = ba; a + b = b + a

6.     Сочетательный закон (закон ассоциативности):

A v (B v C) = (A v B) v C

A & (B & C) = (A & B) & C

Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или расставлять их произвольно.

В математике: (ab)c=a(bc); (a+b)+c =a+(b+c)

7.     Распределительный закон (дистрибутивности):

A v (B & C) = (A v B) & (A v C)

A & (B v C) = (A & B) v ( A & C)

В алгебре логики  можно выносить за скобки общие множители и общие слагаемые.

В математике за скобки можно выносить только общие множители: ab + bc = b(a + c)

8.     Законы де Моргана:

9.     Законы поглощения:

Av (A & B) = A                  A & (A v B) = A

10. Законы идемпотентности:

A v A = A                 A & A = A

11. Свойства конъюнкции и дизъюнкции:

A v 0 = A         A & 0 = 0      A v 1 = 1           A & 1 = A

Применение законов алгебры логики для упрощения логических выражений

1.      Упростить логическое выражение:

= {7} =  = {3} =   = A

{7} – распределительный закон

{3} – закон исключенного третьего:

Для более наглядного восприятия заданное выражение можно записать, используя математические знаки действий:

2.     Упростить логическое выражение:

Способ 1. Применим закон дистрибутивности:

= {7} =  = {2} = A v 0 = A

Способ 2. Перемножим скобки на основании закона дистрибутивности:

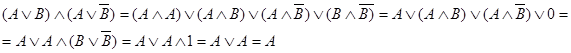
Запишем данное выражение, используя знаки математических действий:

Скачано с www.znanio.ru