Учебно-методический материал по информатике и ИКТ "Алгебра логики" теория, 2 часть, для 7-11 классов

 

 

 

 

 

 

УЧЕБНО-МЕТОДИЧЕСКИЙ МАТЕРИАЛ ПО ИНФОРМАТИКЕ И ИКТ

 

 

«АЛГЕБРА ЛОГИКИ»

 

 

 

Теория

2 часть

 

 

 

СОДЕРЖАНИЕ:

 

1.     Решение задач с помощью кругов Эйлера                                          - 2

2.     Решение логических задач табличным способом                              -17

3.     Логические элементы компьютера                                                     - 30

 

 

 

 

1.Решение задач с помощью кругов Эйлера

Леонард Эйлер, крупнейший математик XVIII в., родился в Швейцарии в 1707г. В 1727 г. по приглашению Петербургской академии наук он приехал в Россию. В Петербурге Эйлер попал в круг выдающихся ученых: математиков, физиков, астрономов, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира. Научное наследие Эйлера поражает своим объемом и разносторонностью. В списке его трудов более 800 названий. Полное собрание сочинений ученого занимает 72 тома. Среди его работ - первые учебники по дифференциальному и интегральному исчислению. В теории чисел Эйлер продолжил деятельность французского математика П. Ферма.

      Эйлер много работает в области математического анализа. Ученый впервые разработал общее учение о логарифмической функции. В геометрии Эйлер положил начало совершенно новой области исследований, выросшей впоследствии в самостоятельную науку-топологию.

    Имя Эйлера носит формула, связывающая число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника: В -Р + Г = 2. Даже основные результаты научной деятельности Эйлера трудно перечислить. Здесь и геометрия кривых и поверхностей, и первое изложение вариационного исчисления с многочисленными новыми конкретными результатами. У него были труды по гидравлике, кораблестроению, артиллерии, геометрической оптике и даже по теории музыки. Он впервые дает аналитическое изложение механики вместо геометрического изложения Ньютона, строит механику твердого тела, а не только материальной точки или твердой пластины. Одно из самых замечательных достижений Эйлера связано с астрономией и небесной механикой. Он построил точную теорию движения Луны с учетом притяжения не только Земли, но и Солнца. Это пример решения очень трудной задачи.

       Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже не писал сам, а диктовал ученикам, которые проводили за него наиболее громоздкие вычисления.

С1761 по 1768 год им были написаны знаменитые «Письма к немецкой принцессе», где Эйлер как раз и рассказывал о своем методе, об изображении множеств в виде кругов. Именно поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал, что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши рассуждения».       

  После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шредер (1841 – 1902). Этот метод широко используется в его книге «Алгебра логика». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.

Одним из основных понятий, которые используются в математике, является понятие множества. Для него не дается определения. Можно пояснить, что множеством называют произвольную совокупность объектов, а сами объекты – элементами данного множества. Так, можно говорить о множестве учеников в классе (элементы – ученики ),множестве дней недели (элементы – дни недели ), множестве натуральных делителей числа 6 (элементы – числа 1, 2, 3, 6 ) и т. д.

        В курсах алгебры и алгебры начало анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.

       Как правило, множества обозначают прописными буквами латинского алфавита.

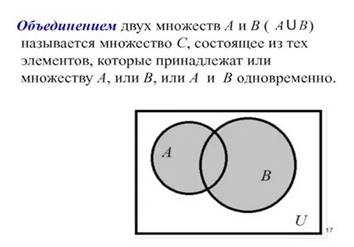
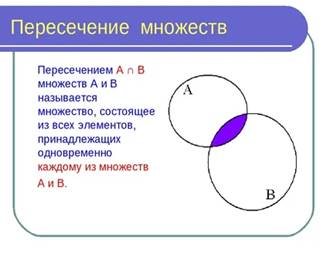
Над множествами можно выполнять определенные действия: находить их    пересечение, объединение. Дадим определение этих операций и проиллюстрируем их с помощью кругов.

 

 

 

 

 

 Задача № 1.

Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 - и значки, и марки.

Остальные не увлекаются коллекционированием. Сколько  школьников не увлекаются коллекционированием.

Решение.

 

В условии этой задачи не так легко разобраться. Если сложить 23 и 35, то получится больше 52. Это объясняется тем, что некоторых школьников мы здесь учли дважды, а именно тех, которые собирают и значки, и марки.

чтобы легче решать задачу, представим ее данные на следующей схеме

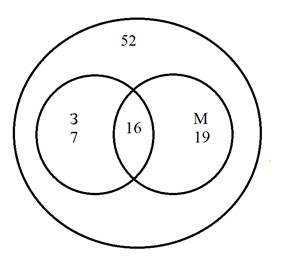На этой схеме большой круг означает всех школьников, о которых идёт речь. Круг З изображает школьников, собирающих значки (всего их 23), а круг М - школьников, собирающих марки (всего их 35). В пересечении кругов З и М стоит число 16 - это те, кто собирает и значки, и марки. Значит, только значки собирает 23 - 16 = 7 человек, только марки собирает 35 - 16 = 19 человек. Всего марки и значкисобирает19 + 7 + 16 = 42 человека. Остаётся 52 - 42 = 10 человек, не увлечённых коллекционированием. Это число можно вписать в свободное поле круга.    Ответ: 10 человек.

 

 

Задача 2.

 

В классе 15 мальчиков. Из них 10 человек занимается волейболом и 9 баскетболом. Сколько мальчиков занимается и  тем, и другим?

Решение.

Изобразим условие с помощью кругов Эйлера .  Этот рисунок подсказывает нам рассуждения. Разберём это рассуждение и впишем нужное число в каждую из образовавшихся на диаграмме частей .

Пусть всеми видами спорта занимаются  х мальчиков. Тогда  только волейболом  занимаются (10-х) мальчиков, а только баскетболом (9-х) мальчиков. Составим уравнение: 10-х + х+ 9-х=15, откуда х=4

 

 

                  В

                       10-х                            Б

                                      х               9-х

 

Ответ: 4 человека.

Задача № 3.

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Чучело», 11 человек – фильм «Выше неба», из них 6 смотрели и «Чучело», и «Выше неба». Сколько человек смотрели только фильм «Выше неба»?

Решение:  Чертим два множества таким образом:  6 человек, которые смотрели фильмы «Чучело» и «Выше неба», помещаем в пересечение множеств.

15 – 6 = 9 – человек, которые смотрели только «Чучело».
11 – 6 = 5 – человек, которые смотрели только «Выше неба».

 Получаем:
                                  

                                            

  Ответ. 5 человек смотрели только «Выше неба».

Задача № 4.

В группе из 80 туристов, приехавших на экскурсию в Москву, 52 хотят посетить Большой театр, 30 - Художественный театр, 12 хотят посетить оба театра, остальные в театры ходить не хотят. Сколько человек не собирается идти в театр?

Решение.

Только большой театр посетят: 52-12=40 туристов;

только художественный театр посетят

 30-12=18 туристов;

80-(40+18+12)=10 туристов не собираются идти в театр.

 

 

 

                        

      Ответ: 10 человек.

 

Задача № 5.

На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал Рон?

Решение.

Учитывая условия задачи, чертеж будет таков:

                         

 

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри.

Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал Рон.                                        

 Ответ. 8 книг прочитал Рон.

Задача№6.

       Сколько человек  участвует в прогулке, если известно, что 16 из них взяли бутерброд с  ветчиной, 24 - с колбасой, 15 - с сыром,  11 и с  ветчиной, и с колбасой,  8 и с ветчиной, и  с сыром,  12 и с колбасой, и с сыром, 6-бутерброды всех видов, а  5- взяли пирожки?                                                                                                                            Решение:  Изобразим множества следующим образом:     

16+24+15-11-8-12+6=30(чел)  -   участвовали в прогулке и с собой брали бутерброды или  3+2+6+5+7+6+1=30(чел)

30+5=35(чел)  -  участвовали в прогулке
Ответ. 35 человек

 

Задача № 7.

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение. Д - драмкружок; Х - хор; С - спорт. В круге Д - 27 ребят, в круге Х - 32 человека, в круге С - 22 ученика. Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8-3=5

спортсменов, не поющих в хоре и 6-3=3, не посещающих драмкружок. Легко видеть, что 5+3+3=11 спортсменов посещают хор или драмкружок, 22-(5+3+3)=11 заняты только спортом; 70-(11+12+19+7+3+3+5)=10 - не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.

                        

 

 

 

 

                                                              Ответ: 10 человек.

Задача № 8.

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

 

Запрос	Найдено страниц (в тысячах)
Пушкин	3500
Лермонтов	2000
Пушкин | Лермонтов	4500

Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

У нас всего есть две сущности: "Пушкин" и "Лермонтов". Поэтому рисуем два пересекающихся круга, желательно разными цветами.

 

Объединение двух кругов в общую фигуру, показывает операцию "Пушкин | Лермонтов". Эта операция всегда стремится увеличить площадь, объединить площади других фигур!

Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» "Пушкин | Лермонтов" (4500).

Нужно найти площадь фигуры Пушкин & Лермонтов. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.

Найдём сначала заштрихованную часть. Она равна: площадь правой фигуры (4500) минус площадь левого круга (3500).

Теперь легко найти площадь пересечения. Для этого нужно от площади правого круга вычесть площадь заштрихованной части. Получается:

Пушкин & Лермонтов (Количество страниц) = 2000 - 1000 = 1000

Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.

Ответ: 1000

 

Задача № 9.

 

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

 

Запрос	Найдено страниц (в тысячах)
Кокос | Ананас	3400
Кокос & Ананас	900
Кокос	2100

Какое количество страниц (в тысячах) будет найдено по запросу Ананас?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.

Найдём заштрихованную часть левого круга.

Весь левый круг 2100. Пересечение  равно 900. Заштрихованная часть равна 2100 - 900 = 1200.

После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь правого круга. Для этого нужно от площади объединения отнять площадь заштрихованной части!

Ананас (Количество страниц) = 3400 - 1200 = 2200

Ответ: 2200

 

Задача № 10.

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» - символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

 

Запрос	Найдено страниц (в тысячах)
(Космос & Звезда) | (Космос & Планета)	1100
Космос & Планета	600
Космос & Планета & Звезда	50

Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.

Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического "ИЛИ".

Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).

Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда

Теперь отметим вторую скобку Космос & Планета.

В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического "ИЛИ". Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!

Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.

Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!

Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.

Теперь у нас есть все компоненты, чтобы решить эту задачу.

Найдём заштрихованную область.

Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).

Количество страниц в заштрихованной части = 600 - 50 = 550

Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).

Количество страниц (при запросе Космос & Звезда) = 1100 - 550 = 550

Ответ: 550

Задача № 11.

 

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

 

Запрос	Найдено страниц (в тысячах)
Англия & (Уэльс & Шотландия | Ирландия)	450
Англия & Уэльс & Шотландия	213
Англия & Уэльс & Шотландия & Ирландия	87

 

Какое количество страниц (в тысячах) будет найдено по запросу

Англия & Ирландия?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.

Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.

Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.

Область Уэльс & Шотландия выглядит так:

Добавим к этой области Ирландию через логическое "ИЛИ". Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!

Теперь нужно сделать операцию логического "И" получившийся области с "Англией". Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:

Т.е. это общее между предыдущем серым контуром и красным кругом!

Отметим Англия & Уэльс & Шотландия - это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.

Отметим Англия & Уэльс & Шотландия & Ирландия - это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.

Отметим то, что нужно найти Англия & Ирландия чёрным цветом.

Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!

Найдём, сколько страниц приходится на бирюзовый кусочек:

Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) - Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 - 87 = 126

Найдём искомую чёрную область.

Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) - Количество (для бирюзового кусочка) =
450 - 126 = 324

Это и будет ответ!

Ответ: 324.

2. Решение логических задач табличным способом.

 

Пять простых шагов на пути поиска решения логических задач.
1. Составляйте таблицу, так как в таблице удаётся учесть все возможные варианты.
2. Внимательно читайте каждое утверждение, так как в каждом содержится что-то такое, что позволит вам исключить хотя бы один из вариантов.
3. Старайтесь отыскать ключевое утверждение, оно поможет развязать весь клубок.
4. После того как вы сравнили все утверждения и исключили из них те, невероятность которых была на поверхности, сравните утверждения между собой, установите связи и противоречия.
5. Решение можно найти простым методом последовательных исключений.

Задача 6. После соревнований бегунов на табло появилась надпись:
• Рустам не был вторым.
• Эдуард отстатл от Рустама на два места.
• Яков не был первым.
• Галина не была не первой ни последней.
• Карина финишировала сразу за Яковом.
Кто же победил в этих соревнованиях? Каково было распределение бегунов на финише?

Решение:
Рисуем таблицу, где столбцы –имена детей, а строки – номера мест. Читаем задачу, пошагово анализируем условие и ставим в таблицу «+», если соответствие установлено и «–», если точно соответствия нет.
Так как Рустам не был вторым и Эдуард отстал от Рустама на два места, то Эдуард не может быть ни первым, ни вторым, ни четвёртым.

Яков не был первым и Галина не была не первой ни последней и так как Карина финишировала сразу за Яковом то она не могла быть ни первой ни второй.

Отсюда видно, что Рустам был первым тогда Эдуард (по условию 2) был третьим.

Так как Карина финишировала сразу за Яковом, то очевидно, что Яков был четвёртым, а Карина последней и тогда Галина была второй.
Задача 4.
Шестеро друзей в ожидании электрички заскочили в буфет.
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром.
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье.
• Кирилл ел то же, что и Мила, но без луковых чипсов.
• Егор завтракал тем же что и Аня, но бутерброду с котлетой предпочел картофельные чипсы.
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад.
Из чего состоял завтрак каждого из друзей?

Решение: Так как
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром;
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье;
• Кирилл ел то же, что и Мила, но без луковых чипсов;
• Егор завтракал тем же что и Аня, но бутерброду с котлетой предпочел картофельные чипсы;
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад, то:

Второй раз проанализируем условия.
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром.
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье.
• Кирилл ел то же, что и Мила, но без луковых чипсов.
• Егор завтракал тем же что и Аня, но бутерброду с котлетой предпочел картофельные чипсы и Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром.
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад, то и Кирилл ел то же, что и Мила, но без луковых чипсов.

Третий раз проанализируем условия.
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье.
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад, то и Кирилл ел то же, что и Мила, но без луковых чипсов.
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром

Пример 7. 

В поездке пятеро друзей — Антон, Борис, Вадим, Дима и Гриша, знакомились с попутчицей. Они предложили ей отгадать их фамилии, причём каждый из них высказал одно истинное и одно ложное утверждение:

Дима сказал: "Моя фамилия — Мишин, а фамилия Бориса — Хохлов". Антон сказал: "Мишин — это моя фамилия, а фамилия Вадима — Белкин". Борис сказал: "Фамилия Вадима — Тихонов, а моя фамилия — Мишин". Вадим сказал: "Моя фамилия — Белкин, а фамилия Гриши — Чехов". Гриша сказал: "Да, моя фамилия Чехов, а фамилия Антона — Тихонов".

Какую фамилию носит каждый из друзей?

Решение. Обозначим высказывательную форму "юноша по имени А носит фамилию Б" как А_Б, где буквы А и Б соответствуют начальным буквам имени и фамилии.

Зафиксируем высказывания каждого из друзей:

1.     Д_М   и   Б_Х;

2.     А_М   и   В_Б;

3.     В_Т   и   Б_М;

4.     В_Б   и   Г_Ч;

5.     Г_Ч   и   А_Т.

Допустим сначала, что истинно Д_М. Но, если истинно Д_М, то у Антона и у Бориса должны быть другие фамилии, значит А_М и Б_М ложно. Но если А_М и Б_М ложны, то должны быть истинны В_Б и В_Т, но В_Б и В_Т одновременно истинными быть не могут.

Значит остается другой случай: истинно Б_Х. Этот случай приводит к цепочке умозаключений:
 
Б_Х истинно  Б_М ложно  В_Т истинно  А_Т ложно  Г_Ч истинно  В_Б ложно  А_М истинно.

Ответ: Борис — Хохлов, Вадим — Тихонов, Гриша — Чехов, Антон — Мишин, Дима — Белкин.

 

 

Пример 8.

Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты соглашения о полном разоружении, представленные каждой из стран. Отвечая затем на вопрос журналистов: "Чей именно проект был принят?", министры дали такие ответы:

Россия — "Проект не наш, проект не США";
США — "Проект не России, проект Китая";
Китай — "Проект не наш, проект России".

Один из них (самый откровенный) оба раза говорил правду; второй (самый скрытный) оба раза говорил неправду, третий (осторожный) один раз сказал правду, а другой раз — неправду.

Определите, представителями каких стран являются откровенный, скрытный и осторожный министры.

 

Решение. Для удобства записи пронумеруем высказывания дипломатов:

Россия — "Проект не наш"   (1),   "Проект не США"   (2);
США —   "Проект не России"   (3),   "Проект Китая"   (4);
Китай —   "Проект не наш"   (5),   "Проект России"   (6).

Узнаем, кто из министров самый откровенный.

Если это российский министр, то из справедливости (1) и (2) следует, что победил китайский проект. Но тогда оба утверждения министра США тоже справедливы, чего не может быть по условию.

Если самый откровенный — министр США, то тогда вновь получаем, что победил китайский проект, значит оба утверждения российского министра тоже верны, чего не может быть по условию.

Получается, что наиболее откровенным был китайский министр. Действительно, из того, что (5) и (6) справедливы, cледует, что победил российский проект. А тогда получается, что из двух утверждений российского министра первое ложно, а второе верно. Оба же утверждения министра США неверны.

Ответ: Откровеннее был китайский министр, осторожнее — российский, скрытнее — министр США.

 

Пример 9.

На одной улице стоят в ряд 4 дома, в которых живут 4 человека: Алексей, Егор, Виктор и Михаил. Известно, что каждый из них владеет ровно одной из следующих профессий: Токарь, Столяр, Хирург и Окулист, но неизвестно, кто какой и неизвестно, кто в каком доме живет.

Однако, известно, что:

1.     Хирург живет рядом с Окулистом

2.     Окулист живет правее Столяра

3.     Токарь живет рядом с Хирургом и Столяром

4.     Алексей живет рядом с Токарем

5.     Егор не живет рядом с Хирургом

6.     Михаил живет левее Алексея

Выясните, кто какой профессией обладает, и кто где живет. Ответ дайте в виде заглавных букв имени людей в порядке слева направо.

Например, если бы в домах жили (слева направо) Константин, Николай, Роман и Олег, то ответ был бы КНРО

 

Пример 10.

5 разных человек в 5 разных домах разного цвета, курят 5 разных марок сигарет, выращивают 5 разных видов животных, пьют 5 разных видов напитков. Вопрос: кто выращивает рыбок?

Подсказки:

·         Норвежец живет в первом доме.

·         Англичанин живет в красном доме.

·         Зеленый дом находится левее белого.

·         Датчанин пьет чай.

·         Тот, кто курит Rothmans, живет рядом с тем, кто

·         выращивает кошек.

·         Тот, кто живет в желтом доме, курит Dunhill.

·         Немец курит Marlboro.

·         Тот, кто живет в центре, пьет молоко.

·         Сосед того, кто курит Rothmans, пьет воду.

·         Тот, кто курит Pall Mall, выращивает птиц.

·         Швед выращивает собак.

·         Норвежец живет рядом с синим домом.

·         Тот, кто выращивает лошадей, живет в синем доме.

·         Тот, кто курит Philip Morris, пьет пиво.

·         В зеленом доме пьют кофе.

Решение задачи

Итак, у нас есть 25 позиций, которые необходимо заполнить следующими данными:

·         Национальность: Норвежец, Англичанин, Датчанин, Немец, Швед.

·         Цвет дома: Красный, Зелёный, Белый, Жёлтый, Синий.

·         Марка сигарет: Ротманс, Данхилл, Мальборо, Пелл Мелл, Филипп Моррис.

·         Животное: Кошки, Птицы, Собаки, Лошади, Рыбки.

·         Напиток: Чай, Молоко, Вода, Пиво, Кофе.

По сути, нам надо заполнить вот такую табличку:

Из подсказок сразу же заполняем ряд ячеек таблицы:

·         Норвежец живет в первом доме.

·         Норвежец живет рядом с синим домом.

·         Тот, кто выращивает лошадей, живет в синем доме.

·         Тот, кто живет в центре, пьет молоко.

Раз англичанин живёт в красном доме, значит, норвежец в красном жить не может. Равно норвежец не может жить в синем. Не может он жить и в белом, так как зелёный дом находится левее белового, а дом норвежца — самый левый. В зелёном он тоже жить не может, так как справа от зелёного белый дом, а справа от норвежца — синий. Значит, он живёт в жёлтом. Отсюда же делаем и вывод, что норвежец курит Данхилл.

Далее, раз зелёный дом находится левее белого, значит, у него номер либо 3, либо 4. Однако в третьем, среднем, доме пьют молоко, а в зелёном доме пьют кофе — значит номер зелёного дома = 4. Значит, белый дом у нас идёт под номером 5, а красный — под номером 3. Здесь же живёт англичанин. Кофе пьют в 4 доме.

Далее, раз немец курит Мальборо, то он не курит Филипп Моррис, и потому не пьёт пиво. Не пьёт он и молоко, которое пьёт англичанин. Не пьёт и чай — это делает датчанин. Значит, немец пьёт либо воду, либо кофе. Норвежец не может пить пиво (он курит другие сигареты), молоко (не англичанин), кофе (живёт не в зелёном доме), чай (не датчанин). Значит норвежец пьёт воду, а потом немец пьёт кофе, и живёт в зелёном доме. Плюс не забываем, что немец курит Мальборо. И раз воду у нас пьёт норвежец, то его сосед (второй дом) курит Ротманс.

Раз швед у нас выращивает собак, то он не может жить во втором доме (там выращивают лошадей), значит он живёт в пятом доме (белом). Значит во втором доме живёт датчанин, который пьёт чай.

Раз курильщик Пелл Мелл выращивает птиц, то это не швед, а значит — англичанин. Следовательно, швед курит Филипп Моррис и пьёт пиво.

И теперь у нас осталась последняя подсказка:

·         Тот, кто курит Rothmans, живет рядом с тем, кто выращивает кошек.

Ротманс курит датчанин, что живёт во втором доме. Справа от него живёт англичанин, который выращивает птиц, значит, второй сосед датчанина (слева), норвежец, этих кошек и выращивает. А потом рыбок выращивает немец. Ответ найден.

ОТВЕТ: НЕМЕЦ

 

Пример 11.

 

1.     На улице находятся 5 домов.

2.     Англичанин живет в красном доме.

3.     Хозяин собаки — испанец.

4.     Живущие в доме зеленого цвета употребляют кофе.

5.     Украинец любитель чая.

6.     Зеленый дом располагается правее от дома цвета слоновой кости.

7.     Предпочитающий сигареты, Олд Голд содержит улиток.

8.     В желтом доме курят сигареты марки Кулз.

9.     Посередине пьют молоко.

10. В доме № 1 живет норвежец.

11. Курящий Chesterfields приходится соседом тому, кто содержит лису.

12. Сигареты Кулз курят в доме, следующим за домом, где живет лошадь.

13. Курящий Лаки Страйк пьет апельсиновый сок.

14. Японец предпочитает сигареты Parlament.

15. Норвежец — сосед синего дома.

 

Вопросы, на которые необходимо получить ответы по завершению:

1.     Кто же из этих жильцов пьет воду?

2.     Кто является владельцем зебры?

 

Пояснение: все 5 указанных домов имеют индивидуальную окраску, в них живут люди нескольких национальностей, содержащие по одному домашнему питомцу. Они любители различных напитков и курят разные типы сигарет. Для более краткого описания дом цвета слоновой кости дальше упоминается как белый.

 

Последовательность логических умозаключений

Для того чтобы найти верное решение, нужно поэтапно вписывать известные данные в таблицу, предварительно исключив из списка невозможные варианты.

Этап I

По задаче (пункт 10), норвежец в доме № 1. За точку отсчета можно принять любое направление, которому нужно следовать на протяжении всего процесса.

Из пунктов 10 и 15 можно сделать вывод, что дом № 2 - синий. А какой цвет у дома норвежца? Из головоломки ясно, что его дом не будет зеленым или белым, так как эти здания стоят рядом. На это прямо указывает пункт 6 и предыдущее решение о том, что дом номер два синего цвета. В красном — англичанин, значит, жилье норвежца будет другого цвета. Остается лишь один вариант. Первый дом — желтый. Благодаря этому выводу ясно, что житель дома номер один курит Kools, а в доме № 2 живет лошадь.

 

Следующий вопрос, на который предстоит найти правильный ответ, гласит: «Что может пить норвежец, находящийся в доме № 1 желтого цвета и курящий сигареты Kools?». Есть данные, которые говорят о том, какие напитки считаются у жильцов любимыми. Украинец отдает предпочтение чаю, а кофе постоянно пьют в доме зеленого цвета. Также понятно из пункта 3, что в доме № 3 пьют только молоко. А вот человек, курящий Lucky Strike, пьет сок. Рассмотрев все варианты, можно понять, что воду употребляет норвежец. Что и требовалось узнать.

дом	1	2	3	4	5
цвет	желтый	синий		?	?
напиток	вода	?	молоко	?	?
животное	?	лошадь		?	?
сигареты	Kools	?		?	?
национальность	норвежец	?		?	?

Этап 2

Теперь нужно попытаться определить, что могут курить в доме номер два, синего цвета, и хозяин которого держит лошадь. Ясно, что Kools курят в доме номер один, а курящий Old Gold занимается разведением улиток. Чтобы продвинуться дальше, предполагается, что хозяин дома № 2 предпочитает Lucky Strike и обычно пьет сок. Если это действительно подходит, то в этом случае кто же в нем живет?

Становится ясно, что его хозяин фактически не может быть норвежцем (10), как и англичанином (2). Он не является испанцем (3), украинцем (5) или японцем (14), так как эти предположения противоречат пунктам условия головоломки, показанным в скобках. Получается, что владелец второго дома не будет курить Lucky Strike.

Маловероятно и то, что владелец второго дома курит Parlament, так как он в этом случае не может пить чай (5), молоко (9), кофе (4) и, конечно же, сок (13).

Исходя из этого, можно утверждать, что хозяин второго дома курит Chesterfield. Теперь нужно выяснить его национальность. Уже известно, что дом синий, а он держит лошадь. Не совпадают четыре условия: он - не норвежец, согласно пункту 10, и явно не англичанин (2), испанец - владелец собаки (3), а японец курит Parlament. Остается лишь один выбор — владелец второго дома — украинец, которому нравится чай.

Так, постепенно можно продвигаться вперед и заполнять по ходу рассуждений все окошки в таблице.

Этап 3

Шаг III необходим, чтобы узнать, в каком из домов живет лиса. Ее могут держать в домах № 1 или № 3, согласно пункту 11, так как в № 2 курят Chesterfield. Путем последовательных исключений можно понять, что лиса у владельца дома номер один.

 

 

 

Этап 4

Для того чтобы узнать, где живет хозяин улиток, курящий Old Gold, нужно выполнить Шаг IV. Предположение, что он пьет кофе, будет неверным, так как это не согласуется с уже полученными данными. Значит, данный человек в третьем доме.

А дальше остается совсем немного поразмышлять и получить правильный ответ. Владелец зебры — японец, который живет в пятом доме зеленого цвета.

 

 

3.Логические элементы компьютера.

 

 

С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.

Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.

Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”).

Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.

Работу логических элементов описывают с помощью таблиц истинности.

 

С х е м а   И . Конъюнктор.

Схема И реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис. 5.1.

Таблица истинности схемы И

Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.

Связь между выходом  z  этой схемы и входами  x  и  y  описывается соотношением:   z = x ^. y (читается как "x и y"). Операция конъюнкции на структурных схемах обозначается знаком  "&"  (читается как "амперсэнд"),  являющимся сокращенной записью английского слова  and.
 С х е м а   ИЛИ. Дизъюнктор.

Схема  ИЛИ  реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы  ИЛИ  будет единица, на её выходе также будет единица.

Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рис. 5.2.   Знак "1" на схеме — от устаревшего обозначения дизъюнкции как   ">=1"  (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1).    Связь между выходом  z  этой схемы и входами  x  и  y   описывается соотношением:  z = x v y  (читается как "x или y").

            

Таблица истинности схемы ИЛИ

 

С х е м а   НЕ. Инвертор.

 

Схема   НЕ  (инвертор) реализует операцию отрицания.  Связь между входом   x  этой схемы и выходом   z  можно записать соотношением   z = , x где      читается как   "не x"   или  "инверсия х".

Если на входе схемы  0,  то на выходе  1.  Когда на входе  1,  на выходе  0.  Условное обозначение на структурных схемах инвертора — на рисунке 5.3

 

Таблица истинности схемы НЕ

 

С х е м а   И—НЕ

 

Схема И—НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом: , где     читается как   "инверсия x и y".   Условное обозначение на структурных схемах схемы   И—НЕ  с двумя входами представлено на рисунке 5.4.

 

Таблица истинности схемы И—НЕ

 

С х е м а   ИЛИ—НЕ

Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора  и осуществляет отрицание результата схемы ИЛИ.     Связь между выходом  z  и входами  x  и  y  схемы записывают следующим образом:  ,  где  ,  читается как  "инверсия  x или y ". Условное обозначение на структурных схемах схемы ИЛИ—НЕ с двумя входами представлено на рис. 5.5.

 

Таблица истинности схемы ИЛИ—НЕ

 

Триггер.

Термин триггер происходит от английского слова trigger — защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает “хлопанье”. Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить (“перебрасываться”) из одного электрического состояния в другое и наоборот.