
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Калязинский колледж им. Н.М. Полежаева
УЧЕБНО – МЕТОДИЧЕСКИЙ КОМПЛЕКС
«МАТЕМАТИКА»
190604 Техническое обслуживание и ремонт автомобильного транспорта
151001 Технология машиностроения
080114 «Экономика и бухгалтерский учет (по отраслям)»
Автор: Старикова Н.В.
Калязин
2013
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Калязинский колледж им. Н.М. Полежаева
«МАТЕМАТИКА»
Калязин
2013
|
Автор: |
Старикова Наталия Валерьевна, преподаватель математики ГБОУ СПО Калязинский колледж им. Н.М. Полежаева
|
|
Рецензенты: |
Чевардина Галина Ивановна, преподаватель математики ГБОУ СПО Калязинский колледж им.Н.М. Полежаева
|
|
|
|
Учебно–методический комплекс «Математика» предназначен для преподавателей математики и студентов 2 курса, обучающихся по специальностям 190604, 151001, 080114.
Комплекс включает в себя: учебное пособие «Математика», методические указания по написанию практических работ; фонд оценочных средств: контрольно-оценочные средства для подготовки промежуточной аттестации; контрольно-оценочные средства для проведения промежуточной аттестации, сборник с практическими и контрольными работами; рабочую программу по предмету, справочное пособие и глоссарий.
Комплекс предназначен для методического обеспечения учебного процесса. Составлен в соответствии с федеральными государственными образовательными стандартами СПО по специальностям190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)». Комплекс направлен на приобретение практических навыков при решении прикладных задач. Материалы комплекса могут быть использованы для дистанционной формы обучения студентов.
![]() СОДЕРЖАНИЕ:
СОДЕРЖАНИЕ:
|
№ |
Наименование пособия
|
Предмет, специальность |
Страницы |
||
|
1. |
Рабочая программа. Технологическая карта. |
Математика 2 курс (190604, 151001, 080114)
|
2-17 |
||
|
2. |
Учебное пособие «Математика». |
Математика 2 курс (190604, 151001, 080114)
|
18-94 |
||
|
3. |
Учебно-методическое пособие «Методические рекомендации по написанию практических работ».
|
Математика 2 курс (190604, 151001, 080114) |
95-125 |
||
|
4. |
Фонд оценочных средств (ФОС).
|
Математика 2 курс (190604, 151001, 080114) |
127-219 |
||
|
|
4.1.Учебно-практическое пособие «Контрольно-измерительные материалы для подготовки промежуточной аттестации».
|
131-145 |
|
||
|
4.2.Учебно-практическое пособие «Контрольно-измерительные материалы для проведения промежуточной аттестации».
|
146-187 |
|
|||
|
|
4.3. «Учебно-практическое пособие «Сборник практических и контрольных работ».
|
188-221 |
|
||
|
5. |
Учебно-справочное пособие «Теоретический справочник»
|
Математика 2 курс (190604, 151001, 080114) |
222-229 |
|
|
|
6. |
Учебно-справочное пособие «Глоссарий»
|
Математика
|
230-243 |
|
|
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Калязинский колледж им. Н.М. Полежаева
|
|
|
|
|
|
|
|
РАБОЧАЯ ПРОГРАММа
дисциплины
ЕН.01 «Математика»
190604 Техническое обслуживание и ремонт автомобильного транспорта
151001 Технология машиностроения
080114 «Экономика и бухгалтерский учет (по отраслям)»
Санкт-Петербург
2012г.
Рабочая программа дисциплины разработана в соответствии с требованиями Федерального государственного образовательного стандарта (далее – ФГОС) по специальности среднего профессионального образования (далее – СПО). 190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)».
Организация разработчик:
ГБОУ СПО Калязинский колледж им. Н.М. Полежаева
Разработчик:
Старикова Н.В., преподаватель математики ГБОУ СПО Калязинский колледж им. Н.М. Полежаева
Рабочая программа рассмотрена на заседании предметной цикловой комиссии общих профессиональных дисциплин
СОДЕРЖАНИЕ
|
|
стр. |
1. ПАСПОРТ рабочеЙ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ
|
4 |
2. СТРУКТУРА и содержание УЧЕБНОЙ ДИСЦИПЛИНЫ |
6 |
3. условия реализации учебной дисциплины |
16 |
4. Контроль и оценка результатов Освоения учебной дисциплины5.ТЕХНОЛОГИЧЕСКАЯ КАРТА. |
17
13 |
МАТЕМАТИКА
Рабочая программа учебной дисциплины «Математика» является частью основной профессиональной образовательной программы по специальностям 190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)» относится к федеральному компоненту учебного плана ГБОУ СПО СПБ ТКУиК в соответствии с ФГОС третьего поколения.
Дисциплина «Математика» относится к математическому и общему естественнонаучному циклу.
В результате изучения обязательной части цикла студент должен уметь:
– решать задачи на отыскание производной сложной функции, производгных второго и высшитх порядков; применять основные методы интегрирования при решении задач;
В результате освоения дисциплины студент должен знать:
– значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы
– основные численные методы решения прикладных задач в области профессиональной деятельности
–основные понятия и методы математического анализа,
максимальной учебной нагрузки обучающегося 99 часов, в том числе:
обязательной аудиторной учебной нагрузки обучающегося 66 часов;
самостоятельной работы обучающегося 33 часов.
2. СТРУКТУРА И ПРИМЕРНОЕ СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ «МАТЕМАТИКА»
|
Вид учебной работы |
Объем часов |
|
Максимальная учебная нагрузка (всего) |
99 |
|
Обязательная аудиторная учебная нагрузка (всего) |
66 |
|
в том числе: |
|
|
практические занятия |
20 |
|
контрольные работы |
2 |
|
курсовая работа (проект) (если предусмотрено) |
нет |
|
Самостоятельная работа обучающегося (всего) |
33 |
|
в том числе: |
|
|
самостоятельная работа над курсовой работой (проектом) (если предусмотрено) |
нет |
|
решение задач |
9 |
|
составление практических задач |
2 |
|
составление алгоритма решения |
2 |
|
подготовка сообщений (презентаций) по теории пределов и по теории дифференциального исчисления |
4 |
|
Итоговая аттестация в форме |
экзамен |
« Математика »
|
Наименование разделов и тем |
Содержание учебного материала, лабораторные и практические работы, самостоятельная работа обучающихся, курсовая работа (проект) (если предусмотрено) |
Объем часов |
Уровень освоения |
|
1 |
2 |
3 |
4 |
|
Раздел 1. Пределы. |
|
8 |
|
|
Тема 1.1. Предел последовательности.
|
Содержание учебного материала |
|
|
|
1.Числовая последовательность. Понятие числовой последовательности. Монотонность и ограниченность числовой последовательности. Понятие предела числовой последовательности. Неопределённости видов: бесконечность на бесконечность. |
2 |
2 |
|
|
2.Второй замечательный предел. Решение упражнений на вычисление пределов последовательностей. |
2 |
2 |
|
|
Тема 1.2. Предел функции. |
3.Предел функции. Определение и свойства пределов функции. Вычисление пределов функции в точке и на бесконечности. |
2 |
2 |
|
4.Первый замечательный предел. Решение упражнений по теме. Практическая работа №1. Вычисление пределов последовательностей и функций. |
2 |
2 |
|
|
Самостоятельная работа обучающихся: Подготовка сообщений (презентаций) по теме: «Пределы». |
2 |
|
|
|
Раздел 2.Основы дифференциального исчисления. |
|
8 |
|
|
Тема 2.1. Правила дифференцирования |
Содержание учебного материала |
|
|
|
1.Определение производной. Правила дифференцирования. Дифференцирование основных элементарных функций. |
2 |
2 |
|
|
2. Производная сложной функции. Производная обратной функции. Определение второй производной. Решение упражнений по теме. Практическая работа №2. Нахождение производных функций. |
2
|
2
|
|
|
Самостоятельная работа обучающихся: Выполнение домашних заданий: - решение задач на нахождение производных элементарных функций - подготовка таблиц с формулами производных элементарных функций |
2
|
|
|
|
Тема 2.2 Механический и геометрический смысл производной |
Содержание учебного материала. |
|
|
|
1.Геометрический и физический смысл первой производной. Решение задач по теме. |
2 |
2 |
|
|
2. Геометрический и физический смысл второй производной. Решение задач по теме. Практическая работа №3. Геометрический и физический смысл производной. |
2 |
1 |
|
|
Самостоятельная работа обучающихся: Выполнение домашних заданий: - решение задач на физический и геометрический смысл производной. |
2 |
|
|
|
Раздел 3. Приложение производной к исследованию функций. |
|
14 |
|
|
Тема 3.1 Монотонность функции Экстремумы функции.
|
Содержание учебного материала. |
|
|
|
1. Признаки возрастания и убывания функции. Экстремумы функции. Необходимое и достаточное условие существования экстремума. |
2 |
1 |
|
|
Самостоятельная работа обучающихся: Выполнение домашнего задания: - задачи на нахождение промежутков монотонности функции, экстремумов функции; составление алгоритма нахождения промежутков монотонности функции, экстремумов функции; |
2 |
|
|
|
2. Решение упражнений по теме. Практическая работа №4. Нахождение промежутков монотонности функции. Нахождение экстремумов функции. |
2 |
2 |
|
|
Тема 3.2 Выпуклость графика функции
|
Содержание учебного материала. |
|
|
|
3. Определение промежутков выпуклости графика функции. Точки перегиба. -Практическая работа №5. Вторая производная. Приложение второй производной к исследованию функции. |
2 |
1 |
|
|
Самостоятельная работа обучающихся: Выполнение домашнего задания: - задачи на нахождение промежутков выпуклости графиков функции - составление алгоритма нахождения промежутков выпуклости графиков функции и точек перегиба. |
2 |
|
|
|
Тема 3.3 Наибольшее и наименьшее значения функции. |
Содержание учебного материала. |
|
|
|
4. Нахождение наибольшего и наименьшего значений функции на промежутке. Практическая работа №6. Нахождение наибольшего и наименьшего значений функции на промежутке. |
2 |
2 |
|
|
Самостоятельная работа обучающихся: Выполнение домашнего задания: - задачи на нахождение наибольшего и наименьшего значений функции. - составление алгоритма нахождения наибольшего и наименьшего значений функции. |
2 |
|
|
|
Тема 3.4 Приложение производной к исследованию функций. Построение графиков функций.
|
Содержание учебного материала.
|
|
|
|
5. Построение графиков функций.
|
2 |
2 |
|
|
6. Решение упражнений по теме.
|
2 |
2 |
|
|
7. Рубежный контроль. Контрольная работа №1. |
2 |
2 |
|
|
Самостоятельная работа обучающихся: Выполнение домашнего задания: - построение графиков функций; подготовка к рубежному контролю -подготовка презентаций по теме: «Дифференцирование» |
3 |
|
|
|
Раздел 4. Дифференциал. Первообразная. Интеграл. |
|
6 |
|
|
Тема 4.1 Определение неопределённого интеграла. Нахождение неопределённого интеграла непосредственно и при помощи замены переменной. |
Содержание учебного материала. |
|
|
|
1. Первообразная и неопределённый интеграл. Таблица интегралов. Вычисление интегралов. |
2
|
2
|
|
|
2.Вычисление интегралов способом подстановки. Практическая работа №7 Нахождение неопределённых интегралов |
4 |
2 |
|
|
Самостоятельная работа обучающихся: Выполнение домашнего задания: - вычисление неопределённых интегралов |
2
|
|
|
|
Раздел 5. Определённый интеграл. Решение прикладных задач. |
|
8 |
|
|
Тема 5.1 Понятие определённого интеграла. Формула Ньютона-Лейбница. |
Содержание учебного материала. |
|
|
|
1.Вычисление определённого интеграла при помощи формулы Ньютона-Лейбница.
|
2 |
1 |
|
|
Тема 5.2 Приложение определённого интеграла к решению прикладных задач. |
2.Приложение определённого интеграла к нахождению площадей плоских фигур |
4 |
2 |
|
3.Приложение определённого интеграла к решению физических задач. |
2 |
2 |
|
|
Раздел 6. Численное интегрирование. Численное дифференцирование. |
|
4 |
|
|
Тема 6.1 Понятие численного интегрирования и дифференцирования. |
Содержание учебного интеграла. |
|
|
|
1.Понятие численного интегрирования. Понятие численного дифференцирования. |
2 |
1 |
|
|
|
4.ЗАЧЁТНОЕ ЗАНЯТИЕ. |
2 |
|
ТЕХНОЛОГИЧЕСКАЯ КАРТА ЕН.01. МАТЕМАТИКА (030912; 034702)
|
Наименование раздела/ модуля/темы и № п/п |
Наименование, обязательных для выполнения студентами работ/вид работы студента по дисциплине |
Количество занятий, на которых студент может выполнить тот или иной вид работы |
Максимальное количество баллов за выполнение одного вида работы |
Сумма максимального накопления баллов по виду работы |
Сумма баллов по разделу/ модулю/теме |
|
|
Раздел 1.
Пределы. |
– Практическая работа №1. Вычисление пределов последовательностей и функций. |
1 |
4 |
4 |
8 |
|
|
Самостоятельная работа обучающихся: Подготовка презентации на тему: «Пределы». |
1 |
4 |
4 |
|
||
|
Раздел 2.
Основы дифференциального исчисления. |
Практическая работа№2. Нахождение производных функций. |
1 |
4 |
4 |
11 |
|
|
Самостоятельная работа обучающихся: Решение задач на нахождение производных элементарных функций. |
1 |
1 |
1 |
|
||
|
Подготовка таблиц с формулами производных элементарных функций. |
1 |
1 |
1 |
|
||
|
Практическая работа №3. Геометрический и физический смысл производной. |
1 |
4 |
4 |
|
||
|
Самостоятельная работа обучающихся: Решение задач на физический и геометрический смысл производной. |
1 |
1 |
1 |
|
||
|
Раздел 3. Приложение производной к исследованию функций
|
Самостоятельная работа обучающихся: составление алгоритма нахождения промежутков монотонности функции, экстремумов функции |
1 |
1 |
1 |
19
|
|
|
Практическая работа №4. Нахождение промежутков монотонности функции. Нахождение экстремумов функции.
|
1 |
4 |
4 |
|
||
|
Самостоятельная работа обучающихся: - составление алгоритма нахождения промежутков выпуклости графиков функции и точек перегиба.
|
1 |
1 |
1 |
|
||
|
Практическая работа №5. Вторая производная. Приложение второй производной к исследованию функции.
|
1 |
4 |
4 |
|
||
|
Самостоятельная работа обучающихся: - составление алгоритма нахождения наибольшего и наименьшего значений функции.
|
1 |
1 |
1 |
|
||
|
-Практическая работа №6. Нахождение наибольшего и наименьшего значений функции на промежутке.
|
1 |
4 |
4 |
|
||
|
Самостоятельная работа обучающихся: Составление учебной презентации по теме: «Приложение производной к исследованию функций»
|
1 |
4 |
4 |
|
||
|
Рубежный контроль. Контрольная работа №1.
|
1 |
10 |
10 |
|
||
|
Раздел 4. Дифференциал. Первообразная. Интеграл. |
Самостоятельная работа обучающихся: - составление таблиц неопределённых интегралов -решение задач на неопределённые интегралы
|
1 |
1 |
1 |
5 |
|
|
Практическая работа №7 Нахождение неопределённых интегралов
|
1 |
4 |
4 |
|||
|
Наименование раздела/ модуля/темы и № п/п |
Наименование, обязательных для выполнения студентами работ/вид работы студента по дисциплине |
Количество занятий, на которых студент может выполнить тот или иной вид работы |
Максимальное количество баллов за выполнение одного вида работы |
Сумма максимального накопления баллов по виду работы |
Сумма баллов по разделу/ модулю/теме |
|
|
Рубежный контроль |
Контрольная работа №1 |
1 |
10 |
10 |
10 |
|
|
Личностные качества студента |
Критерии: Выполнение заданий вовремя, посещение занятий, поведение во время занятий, активность на занятиях.
|
в течение обучения |
10 |
10 |
10 |
|
|
Зачет |
Электронное тестирование по всем темам курса в образовательной системе eduhouse.ru.
|
1 |
20 |
20 |
20 |
|
|
Итого, студент максимально, может набрать |
100 баллов |
|
||||
|
|
|
|||||
3. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ ДИСЦИПЛИНЫ
3.1. Требования к минимальному материально-техническому обеспечению
Реализация программы дисциплины требует наличия учебного кабинета математических дисциплин
Оборудование учебного кабинета: таблицы, схемы
3.2. Информационное обеспечение обучения
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы
1.Ермаков В.И. Общий курс высшей математики для экономистов, Ермаков В.И. , М,2008, 656 стр.
ISBN 5-06-003940-4 Настоящее пособие 5-е изд. — 2002 г. — 495 стр.
4. Рудник А.Е., Сборник задач по элементарной математике для техникумов, Рудник А.Е., Клюева Л.А., Мосолова М.С., Наука, 1974, 321 стр
5. Богомолов Н.В., Практические занятия по математике, Богомолов Н.В., Высшая школа, 6-е, стереотипное , 2003, 212 стр.
Справочная литература:
1) Выгодский М.Я. Справочник по высшей математике. Выгодский М.Я.-М.: Наука, 2007.
2) Ляшко И.И. Справочное пособие по высшей математике. Т.1: Математический анализ. Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П. – М.: Едиториал УРСС, 2008. – 360 с.
4. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ ДИСЦИПЛИНЫ
Контроль и оценка результатов освоения дисциплины осуществляется преподавателем в процессе проведения практических занятий и лабораторных работ, тестирования, а также выполнения обучающимися индивидуальных заданий, проектов, исследований.
|
Результаты обучения (усвоенные умения, усвоенные знания) |
Формы и методы контроля и оценки результатов обучения |
|
1. Знание основных понятий математики. |
1. Наблюдение за решением задач. |
|
2. Знание основ дифференциального и интегрального исчисления. |
2. Защита практических работ № 1, № 2, № 4, № 5, № 6, №3. Контрольная работа№1. |
|
3.Знание основ интегрального исчисления |
3. Защита практической работы №7. |
|
4.Умение решать простейшие прикладные задачи. |
4.Защита практической работы №6. |
|
5. Знание основных понятий теории математики. |
5. Устный опрос. Промежуточная аттестация. |
|
6. Умение применять стандартные методы и алгоритмы к решению задач. |
6. Тестирование. Промежуточная аттестация. |
|
7. Умение пользоваться формулами, графиками, алгоритмами при решении задач. |
7. Самостоятельные, практические работы, контрольные работы. Промежуточная аттестация. |
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Калязинский колледж им. Н.М. Полежаева
УЧЕБНОЕ ПОСОБИЕ
«МАТЕМАТИКА»
190604 Техническое обслуживание и ремонт автомобильного транспорта
151001 Технология машиностроения
080114 «Экономика и бухгалтерский учет (по отраслям)»
Калязин
2013 год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Учебное пособие «Математика» предназначено для преподавателей математики и студентов 2 курса, обучающихся по специальностям 190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)». Пособие может быть так же использовано при дистанционной форме обучения студентов. Пособие предназначено для методического обеспечения учебного процесса; составлено в соответствии с федеральными государственными образовательными стандартами СПО по специальностям190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)». Учебное пособие направлено на приобретение практических навыков при решении прикладных задач.
Учебное пособие «Математика» 2 курс 190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)»
Старикова Наталия Валерьевна.
СОДЕРЖАНИЕ:
Глава 1. Предел последовательности.
§1. Определение предела последовательности. Свойства
пределов. Вычисление пределов видов: ![]() и
и ![]() (Второй замечательный
предел).
(Второй замечательный
предел).
Глава 2. Предел функции.
§1. Определение предела функции. Теоремы о пределах
функций. Вычисление пределов функций. Устранение неопределённости вида ![]() .
.
§2.Первый замечательный предел.
Глава 3. Производная функции. Производная сложной функции.
§1.Определение производной функции. Правила дифференцирования функции. Геометрический и физический смысл производной. Вычисление производной функции.
§2.Производная сложной функции. Вычисление производной сложной функции.
§3.Производная второго порядка. Физический смысл производной второго порядка.
Глава 4.Приложение производной к исследованию функции.
§1. Монотонность функции.
§2.Экстремумы функции.
§3.Наибольшее и наименьшее значения функции.
§5. План исследования функции. Построение графика функции с помощью производной.
Глава 5. Неопределённый интеграл.
§1.Определение неопределённого интеграла. Таблица интегралов. Непосредственное интегрирование. Свойства неопределённого интеграла.
§2.Метод подстановки в неопределённом интеграле.
Глава 6. Определённый интеграл. Применение определённого интеграла к решению прикладных задач.
§1. Определение определённого интеграла. Свойства определённого интеграла. Вычисление определённых интегралов.
§2. Вычисление площадей плоских фигур.
§3.Применение определённого интеграла при решении физических задач.
Задача о вычислении пути.
Глава 7. Численное дифференцирование. Численное интегрирование.
§1.Понятие численного интегрирорвания. Виды численного интегрирования.
§2.Понятие численного дифференцирования.
Глава 8. Дополнительные главы.
§1. Решение прикладных задач.
§2. Приложение дифференциала к приближённым вычислениям.
ГЛАВА 1.
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ.
§1.Числовая последовательность. Монотонность, ограниченность числовой последовательности. Предел последовательности. Теоремы о пределах числовой последовательности.
Определение 1. Бесконечной числовой последовательностью называется числовая функция, определённая на множестве N натуральных чисел.
Пример: (аn): 1; 2; 3; 4; 5; 6…
(bn): 2; 4; 6; 8; 10; 12; …
Определение 2. Последовательность (an) называется возрастающей (убывающей), если каждый её член, начиная со второго, больше (меньше ) предыдущего, т.е. an+1›an ( an+1‹an ).
Замечание. Если выполняется одно из неравенств an+1›an, (an+1≤an), то последовательность называется невозрастающей (неубывающей).
Определение 3. Убывающие, возрастающие, неубывающие и невозрастающие последовательности называются монотонными.
Определение 4. Последовательность an называется ограниченной сверху (снизу), если можно указать такое число М (число m), что для всех членов этой последовательности выполняется неравенство an≤М (an≥m). Числа М и m называются соответственно верхней и нижней границей.
Определение 5. Последовательность an называется ограниченной, если существуют два таких числа m и М, что для всех n выполняется неравенство
m ≤ an ≤ M.
Определение 6. Последовательность an называется постоянной, если все члены её совпадают.
Примеры:
1) (an): 1,2,3,4,5…
Пусть m = 1, так как 1 £ an Þ последовательность ограничена снизу
2) (an) = ![]() : 1;
: 1;![]() ;
; ![]()
Пусть m = 0 и М = 1, так как 0 < an £ 1 Þ последовательность ограничена.
3) (an): 2; 2; 2; 2 …- постоянная последовательность.
Способы задания последовательностей:
1) Формулой,
например: an =
![]()
![]()
![]()
![]()
![]() 2) Графически: х
2) Графически: х
0 1 2
3) Рекуррентный способ: правило, с помощью которого можно вычислить
n-ый член последовательности по известным предыдущим членам:
хn = 3хn + 1 , х1 = 2
Примеры:
1)Доказать, что a![]()
![]() монотонно убывает.
монотонно убывает.
Найдем a![]() =
=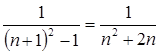
Покажем, что a![]() < a
< a![]() , то есть
, то есть 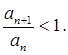
![]()
![]() :
: ![]() =
= 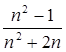 < 1, так как
< 1, так как ![]() , то последовательность (a
, то последовательность (a![]() ) убывает.
) убывает.
2) Доказать, что a![]() =
= ![]() ограничена.
ограничена.
a![]()
![]() последовательность больше 1, m = 1.
последовательность больше 1, m = 1.
a![]() последовательность ограничена сверху и М =
2
последовательность ограничена сверху и М =
2
![]()
![]()
![]() (а
(а![]() )
- ограничена
)
- ограничена
Упражнения:
1) Вычислить первые три члена последовательности:
1) х![]() 5) х
5) х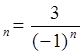
2) х![]() 6) х
6) х![]()
3) х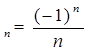 7) х
7) х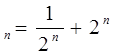
4) х![]() 8)х
8)х![]()
2) Написать общий член последовательности:
1). 1;![]() 5). 1; 3; 5; 7; 9...
5). 1; 3; 5; 7; 9...
2). 1; 7; 13; 19;... 6). 1; 7; 17; 31...
3). 2; 4; 8; 16; 32... 7).-3; 9; -27; 81; -243...
4). 2; 4; 6; 8;
10... 8). 1;![]()
3) Установить вид монотонности:
1). х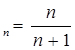 4). x
4). x![]()
2). x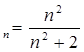 5). x
5). x![]()
3). x![]() 6). x
6). x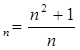
4) Определить ограниченные последовательности:
1). x![]() 5). x
5). x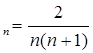
2). x![]() 6). x
6). x![]()
3). x![]() 7). x
7). x![]() =
= ![]()
4). x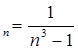 8). x
8). x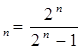
![]()
Определение. Число а называется пределом числовой последовательности
х![]() ,
,![]() если для любого
если для любого ![]()
![]() 0 все члены последовательности х
0 все члены последовательности х![]() , кроме, может быть конечного
числа, лежат в ε - окрестности числа а: (a-ε; a+ε), то
, кроме, может быть конечного
числа, лежат в ε - окрестности числа а: (a-ε; a+ε), то
есть найдётся такое натуральное N, что при n>N выполнено неравенство:
![]() < ε
< ε
Обозначение: ![]()
![]()
![]()
![]()
![]()
Определение. Последовательность, имеющая предел, называется сходящейся, не имеющая предела - расходящейся.
![]() Теоремы
о пределах.
Теоремы
о пределах.
![]() Пусть
Пусть ![]() ,
, ![]() , тогда:
, тогда:
1) ![]()
![]()
Cледствие: ![]()
2) ![]()
3) Пусть b![]() 0 , тогда
0 , тогда 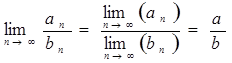
Определение Последовательность называется бесконечно малой, если её предел равен нулю.
Свойства бесконечно малых последовательностей.
1) Сумма двух бесконечно малых последовательностей являются бесконечно малой.
2) Произведение ограниченной последовательности на бесконечно малую является бесконечно малой.
Следствие: Произведение двух бесконечно малых является бесконечно малой.
3) Для того, чтобы выполнялось
равенство ![]() , необходимо и
достаточно, чтобы
, необходимо и
достаточно, чтобы ![]() , где
, где ![]()
Определение. Последовательность ![]() называется бесконечно большой, если
называется бесконечно большой, если ![]()
Примеры: 1) 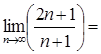
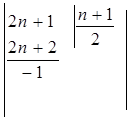 =
=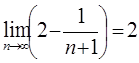 , так как
, так как 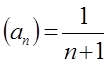 - бесконечно малая величина и:
- бесконечно малая величина и:
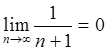
2) 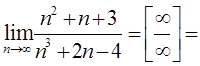 (делим
числитель и знаменатель на
(делим
числитель и знаменатель на ![]()
![]() ) =
) =
= 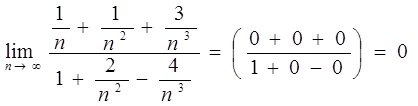
3) 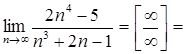
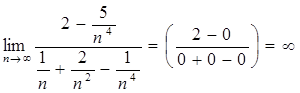
4) 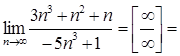
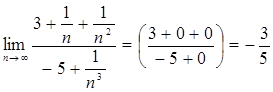
Выводы:
1) Если степень числителя выше степени знаменателя,
то предел последовательности равен ![]() .
.
2) Если степень знаменателя выше степени числителя, то предел последовательности равен нулю.
3) Если старшие степени числителя и знаменателя равны, то предел последовательности равен отношению коэффициентов при старших степенях.
Упражнения: Вычислить пределы.
1.![]() 9.
9. ![]()
2. 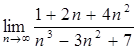 10.
10. 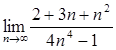
3. 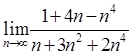 11.
11. 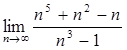
4. ![]() 12.
12. ![]()
5. 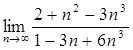 13.
13. 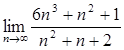
6.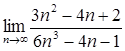 14.
14. 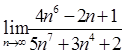
7.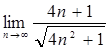 15.
15. 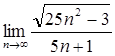
8. 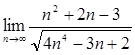 16.
16. 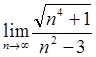
§2. Второй замечательный предел: 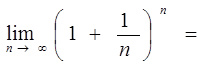 е.
е.
Данный термин, использующийся в российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела.
Замечание: 1) Число е - иррациональное, е ![]() 2,7182818...
2,7182818...
2) Логарифм по основанию е числа в называется натуральным и
обозначается ln b.
Примеры:
1) 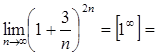 (разделим числитель и знаменатель на 3 ) =
(разделим числитель и знаменатель на 3 ) =
= 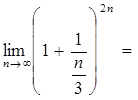 (сравниваем с формулой: показатель
равен знаменателю дроби, уравниваем; затем используем свойства степеней для
того, чтобы степень выражения не изменилась) =
(сравниваем с формулой: показатель
равен знаменателю дроби, уравниваем; затем используем свойства степеней для
того, чтобы степень выражения не изменилась) = 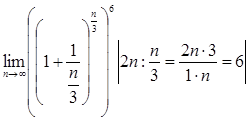 =
= ![]() е
е![]() 2)
2) 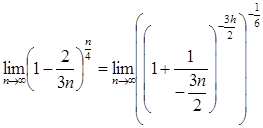
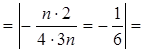 е
е![]() =
= ![]()
3)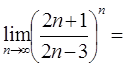
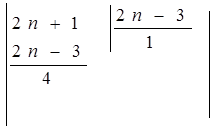 =
=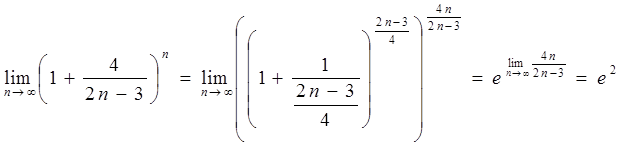
Упражнения: Вычислить пределы.
17. 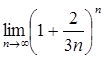 21.
21. 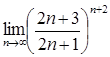 25.
25. 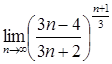
18. 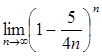 22.
22. 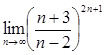 26.
26.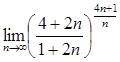
19. ![]() 23.
23. 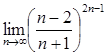 27.
27. 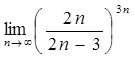
20. 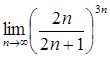 24.
24. 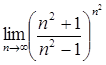 28.
28. 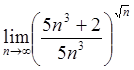
29. 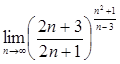 30.
30. 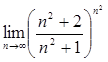 31.
31. 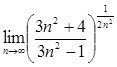
32. 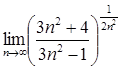 33.
33. 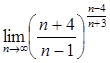
ГЛАВА 2. ПРЕДЕЛ ФУНКЦИИ.
§1.
Определение предела функции. Теоремы о пределах функций. Вычисление пределов
функций. Устранение неопределённости вида ![]() .
.
Пусть функция у = f (х) определена в некоторой окрестности точки х0, быть может, за исключением самой точки х0.
Определение. Число А называется пределом функции
f (х) при х![]() х0, если для любого
ε>0 cуществует такое
х0, если для любого
ε>0 cуществует такое ![]() > 0 , что для всех х,
удовлетворяющих условиям:
> 0 , что для всех х,
удовлетворяющих условиям: ![]() <
< ![]() , х
, х![]() х0 имеет место неравенство
х0 имеет место неравенство ![]() < ε .
< ε . ![]()
Теоремы о пределах функций.
1) ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() где
где
![]() - бесконечно малая функция при
- бесконечно малая функция при ![]()
2) ![]()
3) ![]()
4) 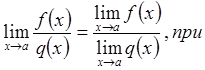
![]() ,
,
![]()
Следствия:
1) Постоянный множитель можно вынести за знак предела.
2) ![]()
3) Предел степени равен степени предела функции.
![]()
Вычисление пределов функций.
1) Предел многочлена.
![]()
То есть, достаточно подставить вместо х единицу, и предел найден.
2) Предел отношения двух многочленов.
1). ![]()
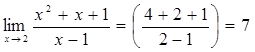
2)Пусть ![]()
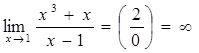
3)Пусть ![]()
![]() и
и ![]() - неопределённость вида
- неопределённость вида ![]()
В этом случае 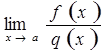 можно вычислить разложением
многочленов
можно вычислить разложением
многочленов ![]() и
и ![]() на множители или заменой у = x- a
на множители или заменой у = x- a
1 способ 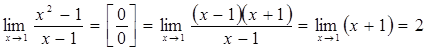
![]()
2 способ 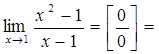 ( пусть y = x-1
( пусть y = x-1![]() при х
при х ![]()
= 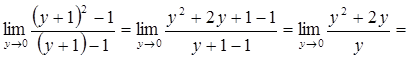
= 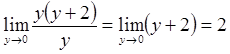
4) Предел отношения
многочленов ![]() при
при ![]() смотри п(1).
смотри п(1).
5) Вычисления некоторых иррациональных функций:
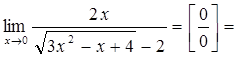 (умножаем числитель и знаменатель на выражение, сопряжённое
знаменателю)=
(умножаем числитель и знаменатель на выражение, сопряжённое
знаменателю)= 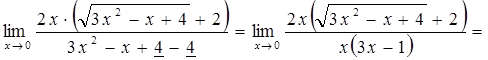
= 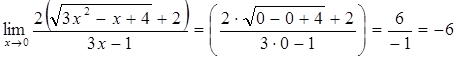
Упражнения: Вычислить пределы функций.
34)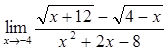 48)
48) 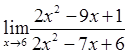
35) 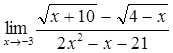 49)
49) ![]()
36) 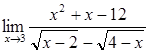 50)
50) ![]()
37) 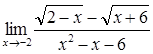 51)
51) 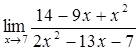
38) 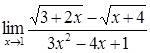 52)
52) ![]()
39) 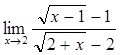 53)
53) 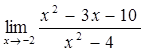
40)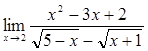 54)
54) 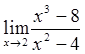
41)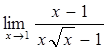 55)
55)
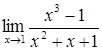
42) 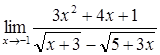 56)
56) 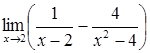
43) 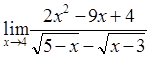 57)
57) 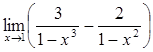
![]()
![]()
44) 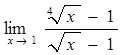 58)
58)
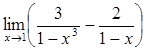
45) 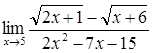 59)
59) 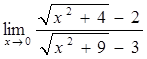
46) 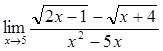 60)
60) 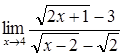
47) 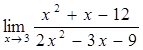 61)
61)
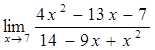
§2.Первый замечательный предел. Вычисление пределов.
Данный термин, использующийся в российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела.
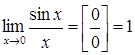
Примеры:
1) 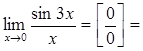 (умножим числитель и знаменатель на 3) =
(умножим числитель и знаменатель на 3) =
= ![]()
2) 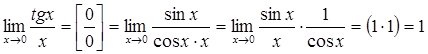
3) 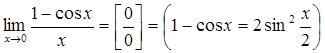 =
=
= 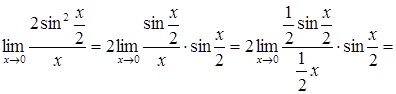
= 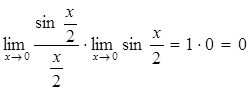
4) 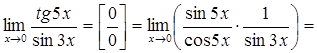 (умножим числитель и знаменатель на"x")=
(умножим числитель и знаменатель на"x")=

=![]()
5) 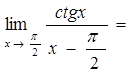 ( ]
( ] ![]() т.к.
т.к.![]() то
то ![]() )
)
![]()
![]()

Упражнения: Вычислить пределы.
62) ![]() 70)
70) 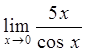 78)
78)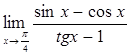
63) 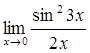 71)
71) 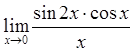 79)
79)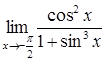
64) 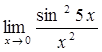 72)
72) 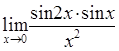 80)
80)![]()
65) 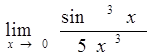 73)
73) 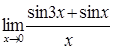 81)
81)![]()
66) 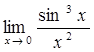
![]() 74)
74)
![]() 82)
82)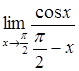
67) 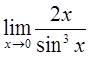 75)
75) 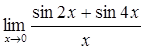 83)
83)![]()
68) 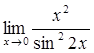 76)
76) 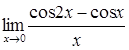 84)
84)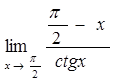
69) 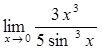 77)
77) 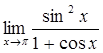 85)
85) 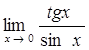
ГЛАВА 3.
ПРОИЗВОДНАЯ ФУНКЦИИ.
§1.Определение производной функции. Правила дифференцирования функции. Геометрический и физический смысл производной.
Вычисление производной функции.
Определение. Производной функции f(x) в точке х0 называется предел отношения
приращения функции ![]() к приращению аргумента
к приращению аргумента ![]() при
при ![]() f/(х0) =
f/(х0) = ![]() =
= ![]() .
.
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ.
|
1. С/ = 0 2. (КХ)/ = К 3. (КХ+В)/ = К 4. (U+V)/ = U/+V/ 5. (U-V)/ = U/-V/ 6. (UV)/ =U/V+V /U (КU)/ = К(U)/ 7. ( 8. 9.(sinx)/ = cosx 10. (cosx)/ = -sinx 11. (tgx)/ = |
12. (ctgx)/ = - 13.(logax)/ = 14.(lnx)/ = 15.(lgx)/ = 16.( 17.(ах)/ = axlna 18.(arctgx)/ = 19. (arcctgx)/ = - 20. (arcsinx)/ = 21.(arccosx)/ = - |
Примеры.
1.(5х3+4х-7)/ = 15х2+4
2.(х3(х8-10х))/ = (х3)/ (х8-10х)+ (х8-10х)/ х3 = 3х2(х8-10х)+(8х7-10)х3=3х10-30х3+8х10-10х3=11 х10-40 х3
3.![]() =
= ![]() =
= ![]() =
= ![]()
4.(2sinx – 5 cosx)| = 2cosx + 5sinx
5.(х + ![]() +
+ ![]() –
– ![]() )/ =(х+х-1+х-2-
)/ =(х+х-1+х-2-![]() )/=1-1х-2-2х-3-
)/=1-1х-2-2х-3-![]() = 1 –
= 1 – ![]() –
– ![]() –
– ![]()
Геометрический смысл производной.
1.Значение производной функции f(x) в точке х0 равна угловому коэффициенту касательной, проведённой к графику данной функции в точке с абсциссой х0.
к = tg![]() =f/(х0)
=f/(х0)
2.Уравнение касательной к кривой, проведённой в точку касания:
у – у0 = у/(х0)(х – х0).
3.Прямая,
перпендикулярная касательной в точке касания, называется нормалью к кривой.
Уравнение нормали: у – у0 = ![]() (х – х0).
(х – х0).
Примеры.
1.Написать уравнения касательной и нормали к графику функции у = х2 + 5 в точке с абсциссой х0 = 2.
Решение:
а) Исходя из уравнения
касательной: у – у0 = у/(х0)(х – х0),
необходимо найти у0 и ![]() (х0).
(х0).
б) у0 =у(х0) = 22+5 = 9
в)![]() = 2х
= 2х
![]() (2) = 4
(2) = 4
г) Подставим полученные значения в формулы касательной и нормали:
|
у – у0 = у/(х0)(х – х0) у – 9 = 4 (х – 2) у = 4х + 1 – уравнение касательной
|
у – у0
= у – 9 = у = уравнение нормали
|
Физический смысл первой производной.
Мгновенная скорость движения точки в любой момент времени t есть производная пути S по времени t: V = S/.
Примеры. Тело движется прямолинейно и равноускоренно по закону
s = 5t2 + 8t + 10(м). Найти:
1.Скорость движения в конце 8 секунды.
2. По истечении скольких
секунд скорость достигнет 128![]() .
.
Решение:
1)V = S/.
V = (5t2 + 8t +
10)| = 10t + 8![]()
V(8) = 10![]() 8 + 8 = 88(
8 + 8 = 88( ![]()
2. V = S/.
V = 10t + 8
V = 128
следовательно: 10t + 8 = 128
10t = 120
t = 12(сек)
Ответ: 1. 88![]() 2. через 12 сек.
2. через 12 сек.
Упражнения: Вычислить производные следующих функций:
86) 5х4 + 6х9 -9
87) 18х2 +16х3 +19
88) (х2-7)(х3 + 9)
89) (4х4-8)(3х3 -10)
90) ![]()
91) ![]()
92) -3х-5 + 15х-4 – 2х-3 + х-1 +2
92) 4х0,75 + 3х0,5 + 4х2 +3х
93).![]()
94) х2![]()
95) ![]()
Решить следующие задачи:
96) Составить уравнение касательной к графику функции у = х3 – 2х2 + 2 в точке х0 = 1.
97) Написать уравнение
касательной у =![]() в точке А(2;3).
в точке А(2;3).
98) Составить уравнение нормали к кривой у = х3 + 4х2 – 1 в точке с абсциссой х0 = -1.
99) Какой угол (острый
или тупой) образует с положительным направлением оси х касательная к графику
функции у = х + ![]() в точке с абсциссой х0 = 2.
в точке с абсциссой х0 = 2.
100) Написать уравнение касательной к графику функции у = х +ln(2х+1) в точке с абсциссой х0 = е.
101) Найти угловой коэффициент к графику функции у = lnx в точке с абсциссой х0 = 1.
102) В какой точке
касательная к кривой у = lnx
наклонена к оси ОХ под углом ![]() .
.
103) Написать уравнение нормали к кривой у = ех в точке с абсциссой 0.
104) В каких точках касательные к кривой у = х3 + х – 2 параллельны прямой у = 4х – 1?
105) Закон движения точки
выражается формулой S = 1 + t2 + ![]() .
.
106) Точка движется по закону S = 0,25(t4 -4t3+2t2 -12t)м. В какой момент времени точка остановится.
107) Какая из этих функций у = 2х + 5, у = ех, у = 0,5х2 имеет наибольшую скорость изменения в точке х0 = 0; 1; 2.
§2.Производная сложной функции.
Теорема. Пусть у = у (U) и U = V(x) – дифференцируемые функции. Тогда
сложная функция у = у (U)
есть так же дифференцируемая функция, причём у/ = ![]() . Эта теорема справедлива для любого конечного числа
дифференцируемых функций, её составляющих.
. Эта теорема справедлива для любого конечного числа
дифференцируемых функций, её составляющих.
Примеры. Вычислить производные сложной функции.
1.((х3 + х2 + 6)4)/ = 4(х3 + х2 + 6)3(3х2 + 2х)
2.(![]() )/ =
)/ = ![]() =
= ![]()
3.(sin3 2x)|
= 3 sin2 2x ![]() cos2x
cos2x![]() 2 = 6 sin2 2x
2 = 6 sin2 2x ![]() cos2x
cos2x
4.(lnlog2
(8x+1))/ = ![]() 8
8
5.(![]() )/ =
)/ = ![]() 4x3
4x3
Упражнения. Вычислить производные функций.
108) (х2+4х)4
109) (зх3+4х4-8)3
110) (9х3+14х4-18)6
111) (![]() -
- ![]() )4
)4
112) ![]()
113) ![]()
114) ![]()
115) х![]()
116) ![]()
117) ln5x
118) ln3x4
119) log3![]()
120) lg![]()
121) lnln(2x+1)
122) ![]()
123) log4![]()
124) ln2x
+ ![]()
125) e-5x![]()
126) ![]()
127) 0,5(e3x + e -3x )
128) lnsinex
129) lnlog3(x3 + x2)
130) lncos![]()
131) sin36x
132) ![]()
![]()
133) ![]()
134) 0,3(lntg2x + lncos23x)
135) lg![]()
136) ![]()
137) ![]()
138) arcctg![]()
139) ![]() - accos
- accos![]()
140) arcsin(3ln2x)
141) Написать уравнение касательной к графику функции:
1)у = ![]() +2х, параллельная прямой у = 4х – 1.
+2х, параллельная прямой у = 4х – 1.
2) у = х2 – ln(2x-1), параллельной прямой у = 2х – 3.
143) Найти угол между касательной к графику функции у = ln(2x + 1) в точке с абсциссой 1.
144) Точка совершает
гармоническое колебание по закону: f(t) = ![]() . Найти скорость в момент времени t1=
. Найти скорость в момент времени t1=![]() c, t2 =
c, t2 = ![]() c, t3 = 1c.
c, t3 = 1c.
§3.Производная второго порядка.
Физический смысл производной второго порядка.
Определение. Производная от первой производной называется второй производной и обозначается: у//.
Производная от второй производной называется третьей производной и т.д.
Физический смысл второй производной.
Вторая производная f//(х) выражает скорость изменения первой производной, то есть ускорение изменения функции у = f(x). а = V/ = S//
Примеры: 1.Найти вторую производную функции: у = sin4x.
y/ = 4cos4x, y// = -16sin4x
2. Найти у//(0), если у = х3 + 2х2.
у/ = 3х2 +4х
у// = 6х + 4
у// (0) = 0 + 4 = 4
Упражнения: Вычислить вторую производную функции:
145) а) 18х2 +16х3 +19 б) 8х4 - 6х5 +180
в) ln4x г)![]()
д) sin26x
е)![]()
ж) х + ![]()
146) Показать, что
функция у = 4![]() - 5х удовлетворяет уравнению:
- 5х удовлетворяет уравнению:
у/// - 3у/ + 2у = 0.
147) По прямой движутся две точки. Определить, в какие моменты времени они будут иметь одинаковые ускорения, если f(x) = t4 + 2t3 + 5t +1, а g(x) = 12t2.
148) Выяснить, удовлетворяет ли функция у = х2 уравнению у// + у/ + 3у = 0.
149) Найти значение третьей производной функции у = xln2x в точке х =2.
150) у = хе2х. Найти: у//(0), у//(1).
151) В какие моменты времени точки будут иметь одинаковые ускорения:
f(x) = et,
g(x) = 5t2 + ![]() t + 0,5.
t + 0,5.
152) S = 2t3 + 4t2 -7(м). Определить ускорение и скорость движения точки через 3 секунды от начала движения.
ГЛАВА 4.
ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ.
§1. Монотонность функции.
Определение. Функция ¦(x) называется возрастающей, если для любого большего значения аргумента х из D(у) соответствует большее значение у.
Определение. Функция ¦(х) называется убывающей, если для любого большего значения аргумента х из D(у) соответствует меньшее значение функции.
Теорема (необходимое условие возрастания функции).
Если дифференцируемая функция ¦(х), х є (a;b) возрастает на интервале (a;b), то ¦’(х0)>0 для ∀х0є (a;b).
Теорема (необходимое условие убывания функции).
Если дифференцируемая функция ¦(х), х є (a;b) убывает на интервале (a;b), то ¦’(х0) <0 для ∀х0 є (a;b).
Теорема (достаточное условие возрастания функции).
Если функция у = ¦(х), х є (a;b) имеет положительную производную в каждой точке интервала (a;b), то эта функция возрастает на интервале (a;b).
Теорема (достаточное условие убывания функции).
Если функция ¦(х), хє(a;b) имеет отрицательную производную в каждой точке интервала (a;b), то эта функция убывает на интервале (a;b).
АЛГОРИТМ:
1.Находим область определения функции.
2.Находим производную функции ¦(х): ¦’(х).
3. Находим корни производной и точки, в которых производная не существует.
4. Наносим на область определения функции полученные точки.
![]()
![]()
![]() 5. Определяем знаки производной
в каждом полученном промежутке.
5. Определяем знаки производной
в каждом полученном промежутке.
6. Если ¦’(х) >0 на (a;b), то ¦(х) возрастает на (a;b).
Если ¦’(х) <0 на (a;b), то ¦(х) убывает на (a;b).
![]()
Пример
1: у = lnх2 - найти
промежутки возрастания и убывания функции.
Корней производная не имеет: х = 0 – точка, в которой производная не существует.
![]()
![]()
![]()
![]() -
+ х
-
+ х
0
Ответ: ¦(х) убывает при х є
(-∞;![]() , ¦(х)
возрастает при х є
, ¦(х)
возрастает при х є ![]() ;+∞).
;+∞).
Пример 2: y = х2 – 2х + 6 D(у)=R
1)у/ = 2х – 2
2) 2х – 2 = 0
х = 1
![]()
![]()
![]()
![]() - 1 + х
- 1 + х
Ответ: ¦(х) убывает при х є
(-∞;![]() , ¦(х)
возрастает при х є
, ¦(х)
возрастает при х є ![]() ;+∞).
;+∞).
Упражнения. Исследовать функцию на монотонность:
153)у = х3 – 3х
154) y = х3+х2-8х+1
155) y = х4-12х2+24х-3
156) y = х4-8х3+22х2-24х+12
157) y = 2х4 – х
158) у = 0,25х4 + 8
159) у = ![]() х3 - 4х
х3 - 4х
160) у = 2х3 – 3х2 – 12х + 8
161) у = 2х3 + 9х2 + 12х -2
162) у = (х+2)2(х-3)3
163) у = ![]()
164) у = ![]()
§2.Экстремумы функции.
Определение. Точка х0 из области определения функции ¦(х) называется точкой минимума этой функции, если найдётся такая б - окрестность
(х0 - б; х0 + б) точки х0, что для всех х≠х0 из этой окрестности выполняется неравенство ¦(х)>¦(х0 ).
Определение. Точка х0 из области определения функции ¦(х) называется точкой максимума, если найдётся такая б - окрестность (х0 - б; х0 + б) точки х0, что для всех х ≠ х0 из этой окрестности выполняется неравенство ¦(х)<¦(х0).
Определение. Точки минимума и максимума называются точками экстремума, а значения функции в этих точках называются экстремумами функции.
Теорема Ферма (необходимое условие существования экстремума).
Если точка х0 является точкой экстремума функции у=¦(х) и в этой точке существует производная ¦’(х0), то ¦’(х0) = 0.
Определение. Точки, в которых производная обращается в ноль или не существует, называются критическими точками (1 рода).
Теорема (достаточное условие существования экстремума).
Пусть функция у=¦(х) непрерывна в х0 и в некоторой её окрестности имеет производную, кроме, может быть самой точки х0, тогда:
1) если производная ¦’(х) при переходе через точку х0, меняет знак с плюса на минус, то х0, является точкой максимума.
2) если производная ¦’(х) при переходе через точку х0 меняет знак с минуса на плюс, то точка х0 является точкой минимума.
3) если производная ¦’(х) при переходе через точку х0 не меняет знак, то в точке х0 функция не имеет экстремума.
АЛГОРИТМ.
1.Находим область определения функции.
2. Находим производную функции у’= ¦’(х).
3. Находим корни производной и точки, в которых производная не существует.
4.Разбиваем полученными точками область определения функции на промежутки.
5. Определяем знак ¦’(х) в каждом из полученных промежутков.
6. Выделяем те точки, в которых функция определена и по разные их стороны производная имеет разные знаки. Это и есть экстремальные точки:
а) Если при переходе через точку х0 ¦’(х) меняет знак с «+» на «-»,
то х0 - точка max
б) Если при переходе через точку х0 ¦’(х) меняет знак с «-» на «+»,
то х0 - точка min.
7. Находим значения функции в точках экстремумов.
Пример: у = ![]() - 2х2 + 3х –
4. Исследовать функцию на экстремум.
- 2х2 + 3х –
4. Исследовать функцию на экстремум.
D(у)=R у’=х2-4х+3
х2-4х+3=0
х1=1, х2=3
![]()
![]()
![]()
![]()
![]()
![]() + max
– min + х
+ max
– min + х
1 3
уmax(1)=-2 2/3 уmin(3)=-4
Пример: у = ![]() .
Исследовать функцию на экстремум.
.
Исследовать функцию на экстремум.
у/ = ![]() =
= ![]() D(у)
= R \ {3}
D(у)
= R \ {3}
Корней производная не имеет, но существуют точки, в которых производная не существует:
![]() (х-3)2=0 х1,2=3
(х-3)2=0 х1,2=3
![]()
![]()
![]() - 3
- х
- 3
- х
При переходе через точку, производная не изменяет свой знак, поэтому в точке х = 3 экстремумов нет.
Ответ: экстремумов не существует.
Упражнения. Исследовать функции на экстремум:
165) у = х2 + 4х
166)у = -х2 + 6х
167)у = х3 – 3х
168)у = - х3 + 3х
169) у = х3+х2-8х+1
170) у = х4-12х2+24х-3
171) у = х4-8х3+22х2-24х+12
172)у =![]()
173)у = ![]()
174)у = 2х4 - 1
175)у = 2х4 – х
176)у = 0,25х4 + 8
177)у = х3 – 4,5х2 + 6х – 2
178)у = ![]() +
+ ![]() - 6х + 1
- 6х + 1
179)у = - ![]() + 3,5х2 – 6х
+ 2
+ 3,5х2 – 6х
+ 2
180)у = х4 -8х3 + 22 х2 – 24х + 12
181)у = (х2 – 8) ех
182)у = ![]()
§3.Наибольшее и наименьшее значения функции.
Если функция у = ¦(х) непрерывна на отрезке [a;b], то на этом отрезке всегда найдутся точки, в которых функция принимает наибольшее и наименьшее значения. Эти значения достигаются в критических точках или на концах данного отрезка.
Наибольшее значение достигается либо во внутренней точке максимума, либо на концах отрезка; наименьшее – либо во внутренней точке минимума, либо на концах отрезка.
АЛГОРИТМ.
1.Находим производную ¦’(х).
2.Находим критические точки (1 рода).
3.Проверяем, какие из значений х принадлежат данной нам области определения.
4.Находим экстремальные значения и значения функции на концах отрезка: ¦(a) и ¦(b).
5.Из найденных значений выбираем наибольшее и наименьшее.
Пример 1: у=-3х²+4х-8, х є [0;1]. Исследовать функцию на наибольшее и наименьшее значения.
у’=-6х+4
–6х+4=0
-6х=4
х=2/3 є [0;1]
у
= - 6![]()
у
(0) = -у(1) = -3 + 4 – 8 = -7 Ответ: унаиб = - 6![]() ; унаим = -8
; унаим = -8
Пример 2. Исследовать функцию на наибольшее и наименьшее значения:
у
= ![]() , х принадлежит
, х принадлежит ![]()
у/
= ![]() =
= ![]()
Критические точки (1 рода):
-х=0 25-х²=0
х1=0 є [-4;4]
х3=-5 є [-4;4]
х2=5 є [-4;4]
¦(0) = 5 – наибольшее, ¦(- 4) = 3 - наименьшее , ¦(4) = 3
Ответ: унаиб.(0)=5; унаим.(-4)=3, унаим.(4)=3.
Упражнения. Исследовать функцию на наибольшее и наименьшее значение:
183)у = х2 -6х + 3, [0;6]
184)у = 0,5х2 - ![]() х3, [1;3]
х3, [1;3]
185)у = 6х2 – х3, [-1;6]
186)у = х3 –3х2 – 9х + 35, [-4;4]
187)у = - х3 +9х2 – 24х + 10, [0;3]
188)у = х3 +3х2 – 9х - 7, [-4;3]
189)у = 6х2 – 3х4 - 1, [-2;2]
190)у = ![]() , х – любое число
, х – любое число
191)у = ![]() , [0;4]
, [0;4]
192)у = хln2х,
[![]() ; е]
; е]
Определение. График функции у=¦(х), х є (a;b) называется выпуклым вверх на интервале (a;b), если график расположен ниже любой касательной, проведённой к графику функции в точках (a;b).
Определение. График функции у=¦(х), х є (a;b) называется выпуклым вниз на интервале (a;b), если он расположен выше любой касательной, проведенной к графику функции в точках (a;b).
Теорема (достаточное условие выпуклости функции).
Если на интервале (a;b) дважды дифференцируемая функция у =¦(х), х є (a;b) имеет отрицательную (положительную) вторую производную, то график функции обращен выпуклостью вверх (вниз).
Определение. Точки, в которых вторая производная равна нулю или не существует, называются критическими точками (2 рода).
Определение. Точкой перегиба называется такая точка, которая отделяет участок выпуклости от участка вогнутости.
Теорема (достаточное условие существования точек перегиба).
Если функция у =¦(х), х є (a;b) дважды дифференцируема на интервале (a;b) и при переходе через х0 є (a;b) вторая производная ¦”(х) меняет знак то точка кривой с абсциссой х =х0, является точкой перегиба.
АЛГОРИТМ.
1. Находим область определения функции.
2. Находим ¦’(х).
3. Находим ¦”(х).
4. Находим критические точки 2 рода.
5. Разбиваем область определения функции полученными точками
на промежутки и определяем знак ¦”(х) в каждом из них:
6. а) если ¦”(х) < 0 на (a;b), то ¦(х) выпукла вниз на (a;b)
б) если ¦”(х) > 0 на (a;b), то ¦(х) выпукла вверх на (a;b)
7. Из критических точек выделяем те, в которых ¦(х) определена и
¦”(х) имеет разные знаки по разным сторонам каждой из них.
8. Находим значения функции в выделенных точках.
Пример: Исследовать функцию на выпуклость и точки перегиба:
у=х²+4х+3 D(у) = R
у’=2х+4
у”=2>0 => кривая выпукла вниз на D(у)
Ответ: кривая выпукла вниз при х є (-∞;+∞).
Пример: Исследовать функцию на выпуклость и точки перегиба:
у=х4-10х³+36х²-31х-37
у’=4х³-30х²+72х-31
у”=12х²-60х+72
Критические точки 2 рода
12х²-60х+72=0
х²-5х+6=0
х1=2 х2=3
![]()
![]()
![]() знак
у//
знак
у//
![]() 2 ∩ 3
2 ∩ 3 ![]()
у(2) = -19 у(3) = 5
Ответ: кривая выпукла вверх при х є (2;3), кривая выпукла вниз при
х є (-∞;2)![]() (3;+∞)
. А(2; -19) и В(3; 5) – точки перегиба.
(3;+∞)
. А(2; -19) и В(3; 5) – точки перегиба.
Упражнения. Исследовать функции на выпуклость и точки перегиба:
193)у = х²+5х+6
194)у = -х²+2х
195)у = х³-6х²+2х-6
196)у = х³-х
197)у = ![]() х³-3х²+8х-4
х³-3х²+8х-4
198)у = х4-10х³+36х²-100
199)у = х4-8х³+10х²-48х+31
200)у = х4-2х³+ 6х – 4
201)у = хех
202)у = ![]()
203)у = ln(x2 + 4)
204)у = ![]()
205)у = хе –х
§5. План исследования функции.
Построение графика функции с помощью производной.
Алгоритм исследования функции.
1. Найти область определения функции D(у).
2. Исследовать функцию на чётность - нечетность, периодичность.
3. Найти промежутки знакопостоянства функции.
4. Найти промежутки монотонности и её экстремумы.
5. Найти промежутки выпуклости и вогнутости, точки перегиба.
6. Найти точки пересечения графика с осями координат (если возможно).
7. Дополнительные точки.
8. Построить график.
Пример. Исследовать функцию у = х3 – 3х2 и построить ее график.
1. Найдём область определения: D(y) = (- ∞; + ∞).
2.
у(-х)
= - х3 – 3х2![]() - функция не является ни
чётной ни нечётной. График симметрии не имеет.
- функция не является ни
чётной ни нечётной. График симметрии не имеет.
3. Исследуем функцию на монотонность и экстремум:
y´ = 3x2 - 6x = 3x(x-2)
3x(x - 2) = 0
x = 0, x = 2 – критические точки функции
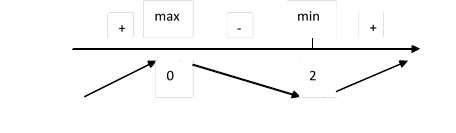
Функция возрастает на промежутках: (- ∞; 0); (2; + ∞).
Функция убывает на промежутке: (0; 2).
Точки экстремума: хmax = 0; xmin = 2.
Экстремумы функции: f(0) = 03 – 3∙02 = 0; f(2) = 23 – 3∙22 = 8 – 12 = - 4.
Точки, соответствующие точкам экстремума: А(0; 0); В(2; - 4).
4. Исследуем функцию на выпуклость
у´´ = 6х – 6
6х – 6 = 0
х = 1 – критическая точка второго рода
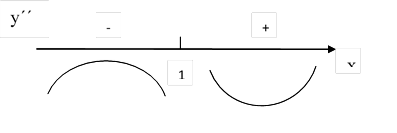
График функции выпуклый вверх на промежутке: (- ∞; 1)
График функции выпуклый вниз на промежутке: (1; + ∞)
f(1) = 13 – 3∙12 = 1 – 3 = - 2
Точка перегиба: С(1; - 2)
5. Дополнительные точки:
х = - 1: f(-1) =( -1)3 – 3∙(-1)2 = - 1 – 3 = - 4; D(- 1; -4)
х = 3: f(3) = 33 – 3∙32 = 27 – 27 = 0; E (3; 0).
6. Построение графика функции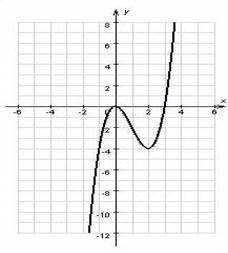
Упражнения. Исследовать функцию с помощью производной и построить ее график:
206.у = -х3 + 3х2 – 4
207.у = 4х2 – х4
208.у = 2х3 – 6х2 + 4
209.у = х4 – 2х3 – 3
210.у = 3х – х3
211.у = 3х2 – 2х3 + 6
212.у = х4 – 2х2 + 1
213.у = х4 – 4х
214.у = 3х4 – 4х3
215.у = - 3х3 + 6х2 – 5х
216.у = ![]()
217.у = ![]() х3 - 4х – 3
х3 - 4х – 3
218.у = х3 + 3х + 2
219.у = (х – 1)3 – 3(х – 1)
220.у = ![]()
221.у = х3 - 4х2 – 3х + 6
222.у = 6х2 - 9х – х3
223.у = 0,1(х4 – 8х2 – 9)
224.На рисунках изображены графики производной функции у = f ´(x). Исследуйте функцию у = f(x) на монотонность и экстремум.
а) 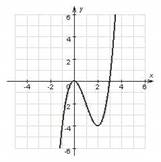
б) 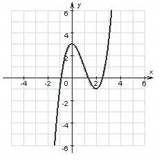
ГЛАВА 5.
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.
§1.Определение неопределённого интеграла. Таблица интегралов. Непосредственное интегрирование. Свойства неопределённого интеграла.
Основной задачей дифференциального исчисления является нахождение производной от данной функции. Рассмотрим обратную задачу, состоящую в отыскании функции по ее производной.
Пример1.
Известно, что производная от некоторой функции F(x) равна![]() :
: ![]() .
Нужно найти функцию
.
Нужно найти функцию![]() . Решением этой
задачи является функция
. Решением этой
задачи является функция ![]() , так
как
, так
как![]() . Следовательно,
. Следовательно,![]() .
.
Пример2.
Дана функция![]() , являющаяся производной
, являющаяся производной
от некоторой функции![]() :
:![]() . Нужно найти функцию
. Нужно найти функцию![]() .
.
Решением этой задачи является
функция ![]() , так как
, так как ![]() .
.
Определение.
Функция![]() называется первообразной
для данной функции
называется первообразной
для данной функции![]() , если ее
производная равна
, если ее
производная равна![]() , т.е.
, т.е.![]() .
.
Так, функция![]() является первообразной для функции
является первообразной для функции![]() , так как
, так как![]() . Функция
. Функция![]() является первообразной для функции
является первообразной для функции![]() , так как
, так как ![]() . Заметим, что одна и та же функция
может иметь несколько первообразных. Так, например, для функции
. Заметим, что одна и та же функция
может иметь несколько первообразных. Так, например, для функции ![]() первообразной является функция
первообразной является функция ![]() , так как
, так как![]() , функция
, функция ![]() также является первообразной для
также является первообразной для ![]() , так как
, так как![]() .
.
Вообще всякая функция вида![]() , где C - произвольная постоянная,
является первообразной для
, где C - произвольная постоянная,
является первообразной для![]() , так
как
, так
как![]() .
.
Определение.
Неопределенным интегралом от функции ![]() называется
семейство ее первообразных функций
называется
семейство ее первообразных функций![]() . Неопределенный
интеграл от функции
. Неопределенный
интеграл от функции ![]() обозначается
так:
обозначается
так: ![]() = F(x)
+ C.
= F(x)
+ C.
Как следует из определения, для
отыскания неопределенного интеграла от данной функции нужно найти какую-нибудь
ее первообразную![]() и затем записать
все семейство первообразных
и затем записать
все семейство первообразных ![]() .
.
Геометрический смысл неопределенного интеграла.
Неопределенный интеграл представляет собой семейство интегральных кривых, каждая из которых получается из любой другой параллельным переносом вдоль оси OY.
Определение. Операция нахождения первообразной для данной функции называется интегрированием этой функции.
Дифференцирование и интегрирование функций – это две взаимно обратные операции.
Свойства неопределённого интеграла.
Свойство1.
Производная от неопределенного интеграла равна подынтегральной функции, т.е.![]() .
.
Следствие.
Дифференциал от неопределенного интеграла равен подынтегральному выражению,
т.е.![]() .
.
Замечание. ![]() .
.
Свойство 2.
Постоянный множитель можно выносить за знак интеграла, т.е. ![]() .
.
Свойство 3.
Неопределенный интеграл от суммы функций равен сумме их неопределенных
интегралов, т.е.![]() .
.
Пример 5.
Найти неопределенный интеграл:![]() .
.
По свойству 2 получаем: ![]() .
.
Пример 6.Найти
следующий неопределенный интеграл ![]() .
.
Используя свойства 2 и 3, получаем: ![]() .
.
Таблица неопределённых интегралов.
1.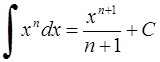 2.
2.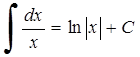
3.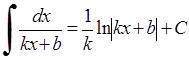 4.
4.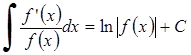
5.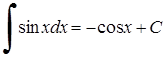 6.
6.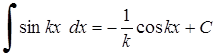
7.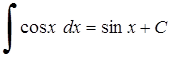 8.
8.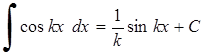
9.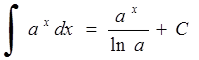 10.
10.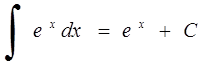
11.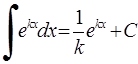 12.
12.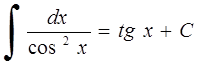
13.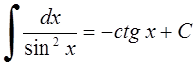 14.
14.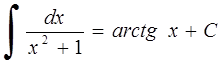
15.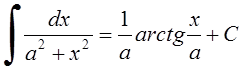 16.
16.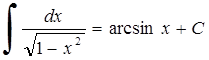
17.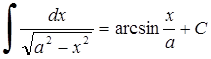 18.
18.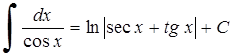
Примеры. Найти интегралы:
1.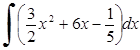 ; 2.
; 2.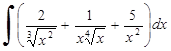 ; 3.
; 3.![]() .
.
Решение.1.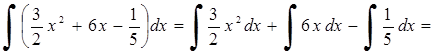
![]() .
.
2. 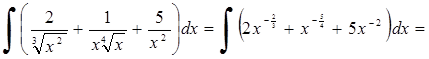
![]() .
.
3. 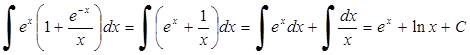 .
.
4. 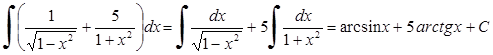 .
.
5. 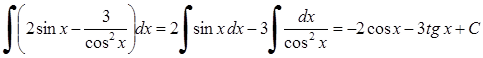 .
.
Упражнения. Найти интегралы:
225)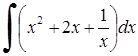 232)
232) 239)
239)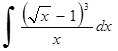
226)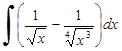 233)
233)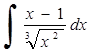 240)
240)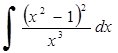
227)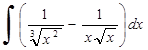 234)
234)![]() 241)
241)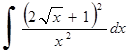
228)![]() 235)
235)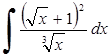 242)
242)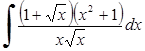
229)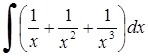 236)
236)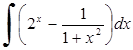 243)
243)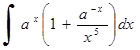
230)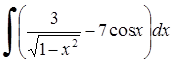 237)
237)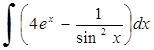
231)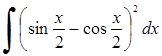 238)
238)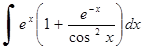
§2.Метод подстановки в неопределённом интеграле.
Теорема. Всякая
формула интегрирования сохраняет свой вид при подстановке вместо независимой
переменной любой дифференцируемой функции от неё, т. е. если:![]() , то и
, то и ![]() ,где
,где ![]() – любая дифференцируемая
функция от х. Это правило очень важно. Основная таблица интегралов в силу этого
правила оказывается справедливой независимо от того, является ли переменная
интегрирования независимой переменной или любой дифференцируемой функцией её.
– любая дифференцируемая
функция от х. Это правило очень важно. Основная таблица интегралов в силу этого
правила оказывается справедливой независимо от того, является ли переменная
интегрирования независимой переменной или любой дифференцируемой функцией её.
Примеры: Вычислить интегралы способом замены переменной.
1.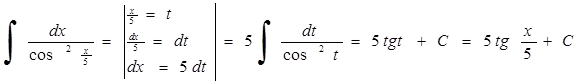 .
.
2.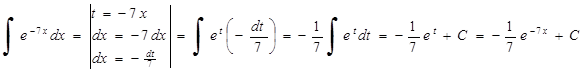 .
.
3.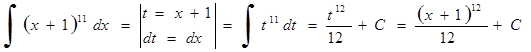
4.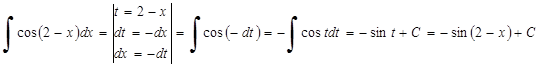
5.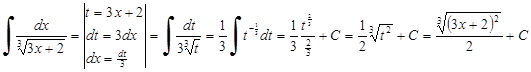
6.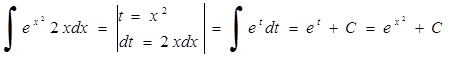
7.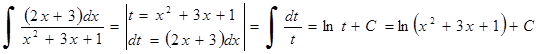
8.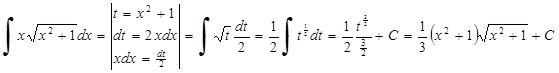
Упражнения. Найти интегралы:
244)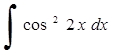 245)
245)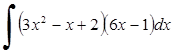
246)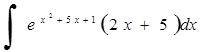 247)
247)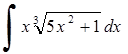
248)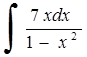 249)
249)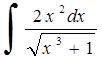
250)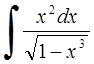 251)
251)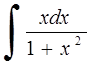 252)
252)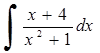
253)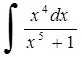 254)
254)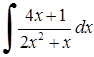 255)
255)![]()
256)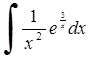 257)
257)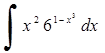 258)
258)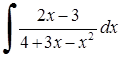
259)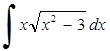 260)
260)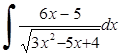 261)
261)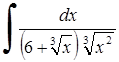
262)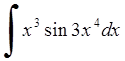 263)
263)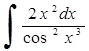 264)
264)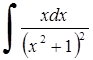
265)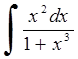 266)
266)![]() 267)
267)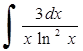
268)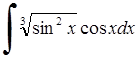 269)
269)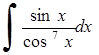 270)
270)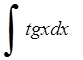
271)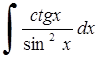 272)
272)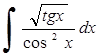 273)
273)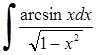
ГЛАВА 6.
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.
§1. Определение определённого интеграла. Свойства определённого интеграла. Вычисление определённых интегралов.
Определение: Определенным интегралом от функции f(x) на отрезке [a , b] называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
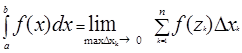
Свойства определённого интеграла.
1.Определенный интеграл от алгебраической суммы
конечного числа функций равен алгебраической сумме определенных интегралов от
слагаемых функций: 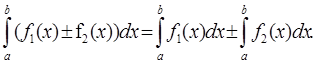
2. Постоянный множитель можно выносить за знак определенного интеграла:
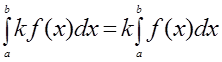
3.При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
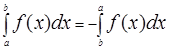
4.Определенный интеграл с одинаковыми пределами равен нулю:
![]()
5.Отрезок интегрирования можно разбивать на части:
![]()
Для вычисления определенного интеграла от функции f(x),
в том случае если можно найти соответствующую первообразную F(x),
служит формула Ньютона-Лейбница: ![]()
т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
Примеры: Вычислить определенные интегралы.
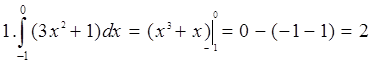
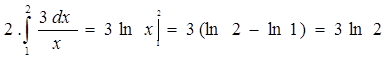
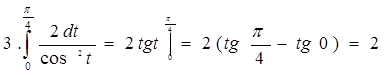
Упражнения. Вычислить интегралы.

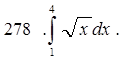
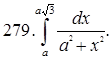
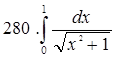
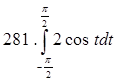
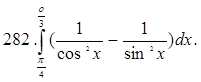
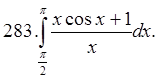
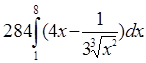
§2. Вычисление площадей плоских фигур.
1.Пусть f(x)>0,
x = a,
x = b,
y =0, тогда площадь фигуры,
ограниченной этими линиями, находится по формуле: 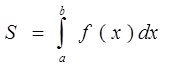
2.Пусть f(x)
<0, x=a,
x=b,
y=0, тогда площадь фигуры,
ограниченной этими линиями, находится по формуле: 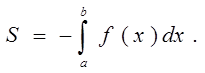
3.Если функция f(x) конечное число раз меняет знак на отрезке [a; b], то формула каждый раз составляется индивидуально с учетом формул (1) и (2).
4. Пусть f(x)
>g(x)
на отрезке [a; b],
тогда площадь фигуры, ограниченной функциями f(x),
g(x),
x = a,
x=b
определяется по формуле: 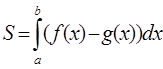
Пример1. Вычислить площадь
фигуры, ограниченной линиями: ![]() , x=0,
x=2, y=0
, x=0,
x=2, y=0
Решение:
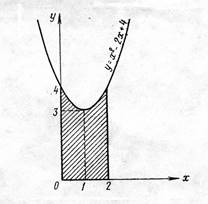
Фигура, площадь которой нужно вычислить, является криволинейной трапецией, ограниченной сверху кривой, снизу осью Ох, слева осью Оу, справа прямой х=2.
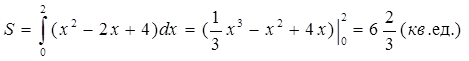
Пример 2. Вычислить
площадь фигуры, ограниченной линиями: 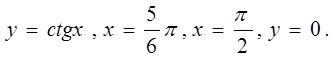
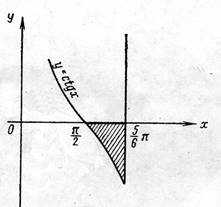
Получилась криволинейная трапеция, ограниченная сверху
осью Ох, снизу котангенсоидой y =
ctgx, справа прямой ![]() .
.![]()
![]() Для
решения задачи применяем вторую формулу, так как криволинейная трапеция
находится ниже оси Ох.
Для
решения задачи применяем вторую формулу, так как криволинейная трапеция
находится ниже оси Ох.
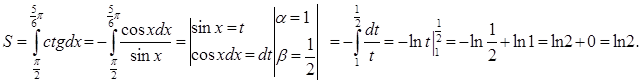 Пример
3. Вычислить площадь фигуры, ограниченной линиями:
Пример
3. Вычислить площадь фигуры, ограниченной линиями: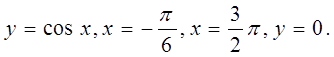
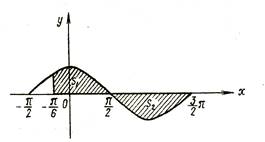
На чертеже видно, что фигура, ограниченная заданными линиями, состоит из двух криволинейных трапеций, одна из которых находится над, а другая под осью абсцисс.
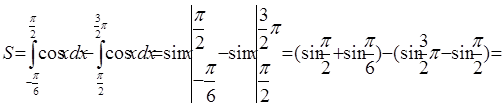 3,5
3,5
Пример 4. Вычислить площадь
фигуры, ограниченной линиями: 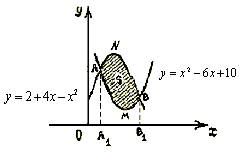
Для построения парабол выделим в правых частях их
уравнений полные квадраты: 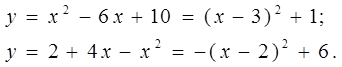
Найдём точки пересечения парабол: Левые части
уравнений равны, значит равны и правые: 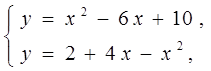
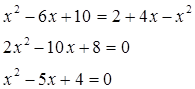
По теореме Виета, определяем: ![]()
Для решения задачи воспользуемся четвёртой формулой: 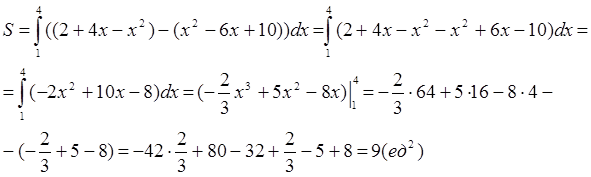
Упражнения. Вычислить площади фигур, ограниченных линиями:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§3.Применение определённого интеграла при решении физических задач.
1. Задача о вычислении пути.
Пусть материальная точка движется прямолинейно с
некоторой скоростью V0
= V(t).Требуется
найти путь, который пройдет эта точка за промежуток времени от t
=
a до t
=
b.Если скорость постоянна, то S
= V![]() (b-a).
Если скорость непостоянна поступают следующим образом: промежуток времени [ а;
в ] разбивают точками t0
= a, t1,…,
t n-1,
tn = b
на n отрезков одинаковой
длины, которая определяется формулой:
(b-a).
Если скорость непостоянна поступают следующим образом: промежуток времени [ а;
в ] разбивают точками t0
= a, t1,…,
t n-1,
tn = b
на n отрезков одинаковой
длины, которая определяется формулой: ![]() ti=
t i-t
i-1=
ti=
t i-t
i-1=![]() , где i
= 1, 2, … , n.Выбрав произвольную
точку с на каждом отрезке [ t i-1,
t i
] , составим сумму:
, где i
= 1, 2, … , n.Выбрав произвольную
точку с на каждом отрезке [ t i-1,
t i
] , составим сумму:![]() V(Ci)
V(Ci)![]() ti.Это
приближение будет тем лучше, чем мельче отрезки разбиения, S
=
ti.Это
приближение будет тем лучше, чем мельче отрезки разбиения, S
=![]()
![]() V(Ci)
V(Ci)![]() ti
.
А этот предел есть определенный интеграл от функции V(t)
на отрезке [
ti
.
А этот предел есть определенный интеграл от функции V(t)
на отрезке [![]() ;
;![]() ] , то есть: S
=
] , то есть: S
= ![]() V(t)dt
.
V(t)dt
.
Пример 1. Тело движется прямолинейно со скоростью V (t) = (3t2 + 4t + 1) м/с. Найти путь, пройденный телом за первые 3 секунды.
S =![]() ( 3t2 + 4t + 1 ) dt =
( t3 + 2t2 + t )
( 3t2 + 4t + 1 ) dt =
( t3 + 2t2 + t )![]() = 48 м.
= 48 м.
Пример 2. Тело движется прямолинейно со скоростью V(t) = (t + 6t 2) м/с. Найти путь, пройденный телом за третью секунду.
S = ![]() ( t
+ 6t2 ) dt
= (
( t
+ 6t2 ) dt
= (![]() t2+
2t3 )
t2+
2t3 ) ![]() = 40,5 м.
= 40,5 м.
Пример 3. Определить максимальную высоту подъема камня, брошенного вертикально вверх со скоростью (18t+3t2 ) м/с.
1.Определим время движения тела от начала движения до остановки:
18t – 3t2 = 0
6t – t2 = 0
t ( 6 – t ) = 0
t1 = 0 t 2= 6
2.Найдем высоту подъема:
H = ![]() (18t
– 3t2) dt
= 9t
(18t
– 3t2) dt
= 9t ![]() - t3
- t3 ![]() = 9(36–0) - (216 –0) =324
–216 = 108 (м).
= 9(36–0) - (216 –0) =324
–216 = 108 (м).
Ответ: 108 метров.
Упражнения. Решить задачи.
299) Скорость движения точки изменяется по закону V= (3t2 + 2t + 1) м/с. Найти путь, пройденный точкой за 10 с от начала движения.
300) Скорость движения точки V = (9t2 - 8t ) м/с. Найдите путь, пройденный точкой за четвёртую секунду.
301) Скорость движения точки V = (12t – 3t2) м/с. Найдите путь, пройденный точкой от начала движения до ее остановки.
302) Скорость движения точки V = (6t2 + 4 ) м/с. Найдите путь, пройденный точкой за 5 с от начала движения.
303) Скорость движения точки V = (18t – 3t2) м/с. Найдите путь, пройденный точкой от начала движения до ее остановки.
304) Скорость движения точки V=(24t – 6t2) м/с. Найдите: 1) путь, пройденный точкой за 3 секунды от начала движения; 2) путь, пройденный точкой за третью секунду; 3) путь, пройденный точкой от начала движения до ее остановки.
305) Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью V = (6t2 + 2t ) м/с, второе – со скоростью V = (4t + 5 ) м/с. На каком расстоянии друг от друга они окажутся через 5с?
306) Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью V = 3t2 м/с, второе – со скоростью V = (6t2 +10) м/с. На каком расстоянии друг от друга они окажутся через 10 с?
307) Два тела движутся по прямой из одной и той же точки. Первое тело движется со скоростью V = (3t2 + 4t) м/с, второе – со скоростью v = (6t + 12) м/с. В какой момент и на каком расстоянии от начальной точки произойдет их встреча?
308) Два тела движутся по прямой из одной и той же точки. Первое тело движется со скоростью V = (3t2 - 6t) м/c, второе – со скоростью V= (10t + 20)м/с. В какой момент и на каком расстоянии от начальной точки произойдет их встреча?
309) Тело брошено с поверхности земли вертикально вверх со скоростью
V = (39,2 – 9,8 t) м/с. Найти наибольшую высоту подъема тела.
310) Тело брошено с поверхности земли вертикально вверх со скоростью
V = (29,4 – 9,8 t) м/с. Найти наибольшую высоту подъема тела.
311) Тело движется прямолинейно со скоростью V(t) = (2t2 + 1) м/с. Найдите путь, пройденный телом за первые 5 секунд.
312) Тело движется прямолинейно со скоростью V(t) = (2t3 + 1) м/с. Найдите путь, пройденный телом за промежуток времени от t = 1с до t = 3c.
313) Скорость тела, движущегося прямолинейно, задается формулой V(t) =
(12t – 3t2) м/с. Найдите путь, пройденный телом от начала его движения до остановки.
314) Два тела начали двигаться по прямой в один и тот же момент из одной и точки в одном направлении соответственно со скоростями V1(t) =(6t2 + 4t) м/с и V2(t) = 4t м/с. Через сколько секунд расстояние между ними будет равно 250 м?
315) Тело движется прямолинейно со скоростью V(t) =(4t+a)м/с. Найдите ускорение а, если известно, что путь, пройденный телом за 2 с от начала движения, равен 48 м.
316) Тело движется по прямой со скоростью V(t) = (6t + 4)м/с. Найдите длину пути, пройденного телом за третью секунду.
317) Найдите путь, пройденный точкой за промежуток времени от t = 0 c до t=5 c, если точка двигалась прямолинейно со скоростью V(t) = (9,8t – 0,003t2) м/с.
Глава 7.
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ.
ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ.
§1.Понятие численного интегрирования. Виды численного интегрирования.
Определенный интеграл вида ![]() c
пределами
интегрирования a и b
можно трактовать как площадь фигуры, ограниченной отрезками прямы х=а и х=в,
осью абсцисс и графиком подынтегральной функции f(x).
Если известна первообразная F(x)
для функии f(x),
то интеграл легко определяется по формуле Ньютона-Лейбница. Для некоторых
подынтегральных функций f(x)
интеграл можно вычислить аналитически, то есть найти в таблице. Однако в общем
случае функция F(x)
может быть не определена: либо первообразные не выражаются через элементарные
функции, либо сами подынтегральные функции не являются элементарными. Это
приводит к необходимости разработки приближенных методов вычисления
определенных интегралов.
c
пределами
интегрирования a и b
можно трактовать как площадь фигуры, ограниченной отрезками прямы х=а и х=в,
осью абсцисс и графиком подынтегральной функции f(x).
Если известна первообразная F(x)
для функии f(x),
то интеграл легко определяется по формуле Ньютона-Лейбница. Для некоторых
подынтегральных функций f(x)
интеграл можно вычислить аналитически, то есть найти в таблице. Однако в общем
случае функция F(x)
может быть не определена: либо первообразные не выражаются через элементарные
функции, либо сами подынтегральные функции не являются элементарными. Это
приводит к необходимости разработки приближенных методов вычисления
определенных интегралов.
Наиболее общеупотребительными приближенными методами вычисления одномерных определенных интегралов являются так называемые классические» методы численного интегрирования по квадратурным формулам: метод прямоугольников, метод трапеций, метод парабол (основанные на суммировании элементарных площадей, на которые разбивается вся площадь под функцией f(x)).
«Классические» методы.
Во всех этих методах отрезок интегрирования [a;
b] разбивается на достаточно большое
число равных частей, на которых строятся искомые площади (рис. 1): h
=![]() и xn
= x0 + nh.
и xn
= x0 + nh.
Оценкой площади под кривой f(x) служит сумма площадей криволинейных трапеций S0; S1…..Sn-1. Простой прием построения формул для расчета интегралов состоит в том, что подынтегральная функция f(x) заменяется
на отрезке [a;
b] интерполяционным многочленом y(x)
и получается приближенное равенство: ![]() .
.
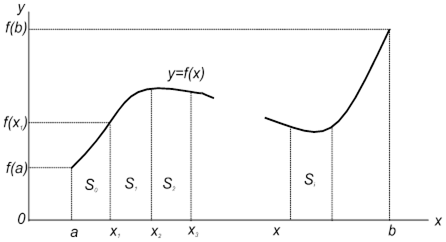 рис.
1
рис.
1
Метод прямоугольников.
Простейшей оценкой искомой площади слижит сумма площадей прямоугольников, заменяющих криволинейные трапеции, как показано на рисунках 2 и 3.
В обычном методе прямоугольников значение f(x) вычисляется в начале каждого отрезка и оценка интеграла дается выражением:
S=S0 +S1 +…. + Sn-1
=![]() , где Si = hf(xi).
, где Si = hf(xi).
Просуммировав элементарные площади фигур, построенных на сегментах [xi;xn-1] получим примерное значение искомого определенного интеграла:
S
= ![]() , где хi=a+ih.
(1
случай).
, где хi=a+ih.
(1
случай).
Погрешность приближения показана на рисунке 2 закрашенной фигурой.
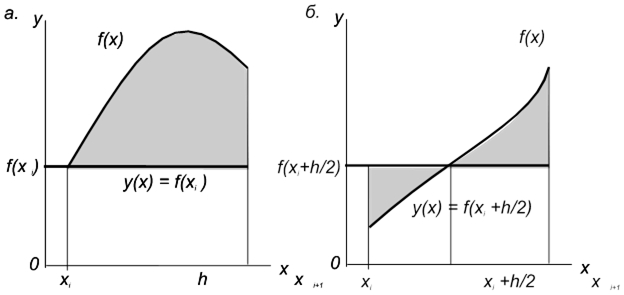
рис 2 рис 3
Одна из модификаций метода прямоугольников заключается в вычислении f(x) не в начальной, а в средней точке каждого отрезка рис 3. В этом случае искомый интеграл оценивается выражением:
S
= ![]() , где хi
=
, где хi
=![]() h.
h.
Метод трапеций.
Другим приближением является формула трапеций, в которой интеграл оценивается вычислением суммы площадей элементарных трапеций со сторонами, равными значениям f(x) в начале и конце элементарного отрезка. Это приближение равносильно замене функции отрезком прямой, соединяющей значения f(x) в начальной и конечной точках отрезка (рис 4).
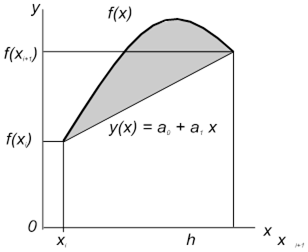 рис
4.
рис
4.
Площадь каждого элементарного сегмента разбиения считается по формуле
S1
= ![]() h, где h =
h, где h =![]() .
.
Просуммируем элементарные площади, то полная площадь
определяетсявыражением: S
= ![]() (f(a)
+ f(b)
+ 2
(f(a)
+ f(b)
+ 2![]() ). Погрешность показана
на рисунке 4 заштрихованной фигурой.
). Погрешность показана
на рисунке 4 заштрихованной фигурой.
Метод Симпсона (парабол).
Более высокую точность расчетов обеспечивает использование параболической (квадратичной) интерполяции по трем соседним точкам отрезка. Уравнение полинома второй степени, проходящего через точки (x0;y0), (x1;y1), (x2;y2) можно записать в виде
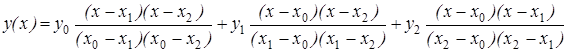
Проинтегрировав данное равенство с учетом того, что ![]() получим
получим ![]() — площадь под параболой
— площадь под параболой ![]() на отрезке [x0;
x2]:
на отрезке [x0;
x2]:
S0 = ![]() =
= ![]() (y0 + 4y1
+ y2) h.
(y0 + 4y1
+ y2) h.
Просуммировав все элементарные площади, получим:
S = ![]() =
= ![]() (f(a) + 4f(a + h)
+ 2f(a + 3h) + 2f(a + 4h) +….+4f(b – h) + f(b),
(f(a) + 4f(a + h)
+ 2f(a + 3h) + 2f(a + 4h) +….+4f(b – h) + f(b),
причем ![]() —
обязательно четное число.
—
обязательно четное число.
Условия применяемости, точность и сходимость классических методов.
А. Практически все выведенные формулы применимы для численного интегрирования достаточно регулярных функций f(x), то есть для функций, которые можно представить полиномом:
![]()
В методе прямоугольников f(x) на каждом малом сегменте заменяется прямой, описываемой первым членом в разложении: y = x0 (рис 2). В методе трапеций для f(x) берутся два члена разложения: y = a0 + a1x (рис 4); метод Симпсона (парабол) учитывает еще и третий член разложения: y = a0 + a1 + a2x2.
Очевидно, что величина погрешности зависит от характера функции f(x), ее поведения на концах отрезка интегрирования, следовательно, никакой численный метод не может быть рекомендован как универсальный. Применение конкретного метода зависит от вида подынтегральной функции.
Б. Не вдаваясь в математические тонкости выведения формул погрешностей вычисления интеграла различными методами, приведем лишь сами формулы. Итак, формулы для оценки погрешности численного интегрирования методом:
1) прямоугольников (обычным и модифицированным)
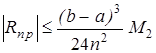
2) трапеций
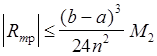
3) Симпсона
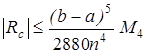
где ![]()
Очевидно, формула Симпсона обладает повышенной точностью:
1.Она оказывается точной для функций, являющихся полиномами до третьей степени включительно, так как для этих случаев производная четвертого порядка равна нулю;
2.Для достижения
той же точности, что и в формуле трапеций, в формуле Симпсона можно брать
меньшее число ![]() отрезков
разбиения.
отрезков
разбиения.
Пример 1. Вычислить интеграл S
= ![]() по формуле трапеций,
разделив отрезок
по формуле трапеций,
разделив отрезок ![]() на 10 равных
частей, и оценить погрешность вычислений. Оценим ошибку метода. Для этого
найдем вторую производную подынтегральной функции: f//
= (2 – х2)sinx
+ 4xcosx. На отрезке [0;
1] вторая производная всюду положительна, причем ее значение ограничено сверху
числом 3,3. Таким образом, используя формулу
на 10 равных
частей, и оценить погрешность вычислений. Оценим ошибку метода. Для этого
найдем вторую производную подынтегральной функции: f//
= (2 – х2)sinx
+ 4xcosx. На отрезке [0;
1] вторая производная всюду положительна, причем ее значение ограничено сверху
числом 3,3. Таким образом, используя формулу ![]() имеем:
имеем:
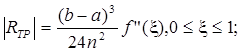
полагая ![]() ,
получим
,
получим 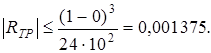
Итак, приняв на заданном участке интегрирования n
= 10, мы сможем получить интеграл от заданной функции с погрешностью, не
превышающей 0,001375, если будем вести вычисления таким образом, чтобы
погрешность округления не исказила окончательный результат в пределах точности
метода. В соответствии с формулой трапеций и учетом рассчитанной ошибки
получим ![]()
Пример 2. Вычислить интеграл из примера 1 по формуле Симпсона, n = 10.
Для оценки остаточного члена найдем производную четвертого порядка от подынтегральной функции f(x) = x2sinx. y//// = (х2 – 12)sinx – 8xcosx.
Производная четвёртой степени ограничена числом 14.
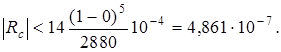
Приведем полученный результат в соответствии с оценкой
![]()
Упражнения:
318) Вычислить определённые интегралы:
|
Вариант |
Подынтегральная функция
|
Пределы интегрирования a b |
|
|
1 |
|
5 |
6,5 |
|
2 |
|
2 |
3,5 |
|
3 |
|
3 |
3,5 |
|
4 |
|
0 |
2 |
|
5 |
|
0,5 |
2 |
|
6 |
|
2 |
2,5 |
|
7 |
|
0 |
1 |
|
8 |
|
|
2 |
|
9 |
|
2 |
5 |
|
10 |
|
0,2 |
0,3 |
|
11 |
|
0 |
|
|
12 |
|
0 |
2 |
|
13 |
|
0 |
|
|
14 |
|
1 |
2 |
|
15 |
|
0 |
1 |
|
16 |
|
0 |
2 |
|
17 |
|
0 |
1 |
|
18 |
|
0,5 |
1 |
|
19 |
|
0 |
|
|
20 |
|
0 |
|
|
21 |
|
0,1 |
0,5 |
|
22 |
|
1 |
2 |
|
23 |
|
0 |
1 |
|
24 |
|
3 |
4 |
|
25 |
|
0,1 |
0,3 |
§2.Понятие численного дифференцирования.
Проектирование
формулы численного дифференцирования получается в результате дифференцирования
интерполяционных формул. Пусть известны значения функции в точках (x1,...,xn)
и требуется вычислить
производную f(k)(x0).
Построим интерполяционный многочлен Pk(x) и положим ![]() .
.
Другой
способ построения формул численного дифференцирования приводит к тем же
формулам - метод
неопределённых коэффициентов. Чаще всего метод используется в многомерном
случае, когда построить интерполяционный многочлен достаточно сложно. В этом
случае коэффициенты численного дифференцирования ci выбираются из того, чтобы формула ![]() была точна для многочленов максимально
высокой степени. Пусть
была точна для многочленов максимально
высокой степени. Пусть ![]() и
потребуем, чтобы для такого многочлена соотношение для f(k)(x) обратилось в равенство:
и
потребуем, чтобы для такого многочлена соотношение для f(k)(x) обратилось в равенство: ![]() .
.
Чтобы
равенство выполнялось для любого многочлена степени m , необходимо и достаточно, чтобы
коэффициенты при aj в
правой и левой частях были равны (xj)(k)= j(j − 1)...(j − k + 1)xj − k.
Получаем систему уравнений: ![]() относительно ci.
Если m = n − 1,
то число уравнений равно числу неизвестных. Определитель системы (определитель
Вандермонда) отличен от нуля , то есть всегда можно построить формулу
численного дифференцирования с n узлами,
точную для многочленов степени n − i.
относительно ci.
Если m = n − 1,
то число уравнений равно числу неизвестных. Определитель системы (определитель
Вандермонда) отличен от нуля , то есть всегда можно построить формулу
численного дифференцирования с n узлами,
точную для многочленов степени n − i.
Формулы численного дифференцирования, получение интерполяционного многочлена.
Приводимые ниже формулы численного
дифференцирования применяются в тех случаях, когда функция y = f(x) задана таблично ( yi= f(xi) в равносторонних узлах ![]() ). 1)
). 1) ![]() (Формула применяется только для
начальных строк таблицы) 2)
(Формула применяется только для
начальных строк таблицы) 2) ![]() (Формула применяется только для
последних строк таблицы)
(Формула применяется только для
последних строк таблицы)
В
середине таблицы применяется формула![]() , полученная путем дифференцирования
инерполяционного многочлена Стирлинга.
, полученная путем дифференцирования
инерполяционного многочлена Стирлинга.
Замечание: Основной принцип численного дифференцирования заключается в
следующем: поскольку любую функцию, заданную таблично, можно представить интерполяционным
многочленом, выбрав какое-нибудь множество из n +1 узлов, то производную от
интерполяционного многочлена ![]() можно использовать в качестве
приближенного применения таблично заданной функции
можно использовать в качестве
приближенного применения таблично заданной функции ![]() . Обычно
формулы численного дифференцирования применяют для нахождения производных в
узлах xi , так как при этом любую точку можно
принимать за начальную, то формулы записывают для x0.
Приближенные формулы нахождения производных второго порядка получается путем
двукратного дифференцирования интерполяционных многочленов Ньютона и Стирлинга.
. Обычно
формулы численного дифференцирования применяют для нахождения производных в
узлах xi , так как при этом любую точку можно
принимать за начальную, то формулы записывают для x0.
Приближенные формулы нахождения производных второго порядка получается путем
двукратного дифференцирования интерполяционных многочленов Ньютона и Стирлинга.
1) ![]() (для начала таблицы)
(для начала таблицы)
2) ![]() (для конца таблицы)
(для конца таблицы)
3)![]() (для середины таблицы)
(для середины таблицы)
При численном дифференцировании таблично заданной функции y = f(x) возникают погрешности двух типов:
§ погрешности усечения
§ погрешности округления
При
оценке погрешности усечения,
оценив на практике, предполагают, что f(x) не
имеет быстро колеблющихся составляющих (период которых не превосходит h).
При этом условии величина разностей определенного может свидетельствовать о
качестве приближения функции f(x) интерполяционным
многочленом подходящей степени. Если разности порядка m различаются меньше, чем на величину
погрешности их округления, то считают, что эти разности практически постоянны и
погрешность усечения не превосходит единицы младшего разряда значений ![]() . С
уменьшением шага расчета погрешность усечения убывает
. С
уменьшением шага расчета погрешность усечения убывает ![]() .
.
Погрешности
округления обратно пропорциональна
шагу расчета h в формулах для первой производной,
обратно пропорциональна h2 в
формулах для второй производной и так далее. Поэтому при уменьшении шага
расчета h погрешность округления увеличивается.
Для оценки используются правила из теории погрешности ![]() .
.
Обобщения
погрешность вычисления производной может рассматриваться как сумма погрешности
усечения и погрешности округления ![]() так как с уменьшением порядка
интерполяции погрешность усечения убывает, а погрешность округления возрастает,
то существует оптимальный шаг расчета, при котором полная погрешность
минимальна:
так как с уменьшением порядка
интерполяции погрешность усечения убывает, а погрешность округления возрастает,
то существует оптимальный шаг расчета, при котором полная погрешность
минимальна:![]() .
.
Пример 1. Найти у / (1) и у // (1) для функции у (х), заданной таблицей:
Значения функции у (х):
|
|
|
|
|
|
|
|
0.96 |
0.7825361 |
|
|
|
|
|
|
|
– 86029 |
|
|
|
|
0.98 |
0.7739332 |
|
– 1326 |
|
|
|
|
|
– 87355 |
|
25 |
|
|
1.00 |
0.7651977 |
|
– 1301 |
|
1 |
|
|
|
– 88656 |
|
26 |
|
|
1.02 |
0.7563321 |
|
– 1275 |
|
|
|
|
|
– 89931 |
|
|
|
|
1.04 |
0.7473390 |
|
|
|
|
Решение. В соответствии с таблицей получим: h = 0,02, х =
1, х0 = 1, следовательно, q = 0. Составив
конечные разности для функции у (х) и используя подчеркнутые
значения, по формуле 1 получим:
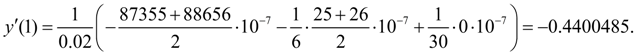
Аналогично, используя выделенные значения по формуле 2 получим:
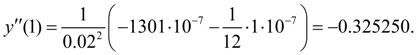
Глава 8. Дополнительная глава.
§1. Прикладные задачи.
Приложение производной в экономической теории.
Пусть q – выпуск
продукции (в натуральных единицах); TR(q) – выручка от продаж; TC(q) – издержки производства,
связанные с выпуском q единиц продукции. Тогда прибыль ![]()
Предположим, что выполняются следующие условия:
Функции TR(q), TC(q) определены
на полуинтервале [0; ![]() и дифференцируемы
при q > 0.
Максимум прибыли достигается в некоторой точке q*
и дифференцируемы
при q > 0.
Максимум прибыли достигается в некоторой точке q*![]() 0. В случае, когда
максимум прибыли положителен
0. В случае, когда
максимум прибыли положителен ![]() , при условии q*
, при условии q*![]() 0 естественным
образом выполняется, поскольку
0 естественным
образом выполняется, поскольку ![]()
![]() (нет выпуска – нет
выручки, нет выручки – нет прибыли). Тогда функция
(нет выпуска – нет
выручки, нет выручки – нет прибыли). Тогда функция![]() дифференцируема
и имеет на интервале [0;
дифференцируема
и имеет на интервале [0; ![]() максимум в
точке q*
максимум в
точке q*![]() 0. По теореме Ферма,
0. По теореме Ферма, ![]() . Так как
. Так как![]() (q)
-
(q)
- ![]() , то в точке q = q* получаем
равенство: TR'(q*)=TC'(q*) или MR=MC.
, то в точке q = q* получаем
равенство: TR'(q*)=TC'(q*) или MR=MC.
В экономической теории данное равенство иллюстрирует один из базовых законов теории производства, согласно которому фирма, максимизирующая свою прибыль, устанавливает объём производства таким образом, чтобы предельная выручка была равна предельным издержкам.
В случае, когда объём производства q не влияет на цену продукции p, имеем TR(q) = p*q, TR'(q) = p.
Равенство TR'(q*) = C'(q*) принимает видp = TC'(q*).
Примеры:
1.Функция спроса имеет вид QD=100 – 20p, постоянные издержки TFC составляют 50 денежных единиц, а переменные издержки TVC на производство единицы продукции – 2 денежные единицы. Найти объём выпуска, максимизирующий прибыль монополиста.
Решение:
Прибыль есть выручка минус издержки:
П=TR – TC, где TR= p![]() Q; TC=TFC+TVC.
Q; TC=TFC+TVC.
Найдём цену единицы продукции:
20p = 100 – Q ![]() p = 5 –
p = 5 – ![]() .
.
Тогда: П=(5 – Q/20)Q – (50 + 2Q)= – Q2 + 60Q - 1000 ® max
Найдём производную: П'(Q)= –2Q+60.
Приравняем
производную к нулю: –2Q+60=0 ![]() Q=30.
Q=30.
При переходе через точку Q=30 функция П(Q) меняет свой знак с плюcа на минус, следовательно, эта точка является точкой максимума, и в ней функция прибыли достигает своего максимального значения. Таким образом, объём выпуска, максимизирующий прибыль, равен 30 единицам продукции.
2. Объём спроса на продукцию предприятия выражается формулой: QD=200 – 4p, а объём предложения – QS=6p – 100. Величина переменных издержек на единицу продукции TVC=25. Чему должна быть равна цена на единицу продукции p, чтобы прибыль П была максимальной?
Решение:
В точке потребительского равновесия QS=QD,
то есть 6p0 – 100=200 – 4p0,откуда p0= 30 (ед.) – равновесная цена,
Ю Q0=80 (ед.) – равновесный объём продукции.
Изобразим графически кривые спроса и предложения, а также точку потребительского равновесия, находящуюся на их пересечении.
Рассмотрим три возможных варианта:
1) p>p0, Ю Q=QD, то есть П = QDp – QD TVC=QD(p – TVC),
подставим значения и получим: П = (200 – 4p)(p – 25)= –4p2 + 300p – 5000.
2) p=p0, Ю Q=QD=QS, Ю Qпродажи=Q0=80 (ед.), Ю
П2=80*(30 – 25)=400 ( ед.).
3) p < p0: Ю Q = QS, то есть П = QSp – QS TVC=QS(p – TVC),
подставим значения: П=(6p – 100)(p – 25)=6p2 – 250p + 2500.
Далее случаи (1) и (3) можно решать аналитически, подставляя различные значения цены из интервала её значений или как-либо иначе, но гораздо проще выявить экстремумы прибыли через производную:
1) П= – 4p2 + 300p – 5000
П'= – 8p + 300;
– 8p + 300=0 Ю p=75/2=37,5 (ед.)
Значит, Q=QD=200 – 4*37,5=200 – 150=50 (ед.),
а П1= – 4p2 + 300p – 5000= – 4*(37,5)2+300*37,5 – 5000=625 (ед.)
2) Во втором случае прибыль была уже найдена: П2=400 (ед.)
3) П=6p2 – 250p + 2500
П'=12p – 250;
12p – 250=0 Ю p=125/6=205/6 (ед.).
Значит, Q=QS=6*205/6 – 100=125 – 100=25 (ед.), a
П3=6p2 – 250p + 2500=6*(205/6)2 – 250*205/6+2500= – 1041/6 (ед.)
Можно заключить, что прибыль максимальна в первом случае, следовательно, цена единицы продукции должна равняться 37,5 денежным единицам.
Приложение производной на оптимизацию площадей, объёмов.
Пример: Обозначив емкость банки
через V см³, сформулируем задачу: Определить размеры цилиндра с объемом V
см³ так, что бы площадь его полной поверхности была наименьшей. Для
решения задачи обозначим радиус основания цилиндра через х, а высоту его через
h (все измерения в сантиметрах). Тогда объем цилиндра: V = ![]()
![]() h =
h = ![]() .
.
Полная поверхность цилиндра:
S = 2![]() x² + 2x
x² + 2x![]() h = 2
h = 2![]() x² + 2
x² + 2![]() x
x![]() = 2
= 2![]() x² +
x² + ![]() =
= 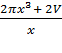
Итак, S(х) = 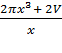
Так как переменная х
может принимать только положительные значения, решение задачи сводится к
нахождению наименьшего значения S(х) на (0;![]() ).
).
Найдем производную
S´(х): S´(х) = 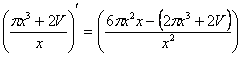 =
= ![]()
Для нахождения
критических точек решим уравнение S´(х) = 0.Корень уравнения: х = ![]() . При х
< 0 <
. При х
< 0 < ![]() S´(х)
< 0, а при х >
S´(х)
< 0, а при х > ![]() S´(х)
> 0.
S´(х)
> 0.
Следовательно, в точке х
= ![]() S(х)
имеет минимум.
S(х)
имеет минимум.
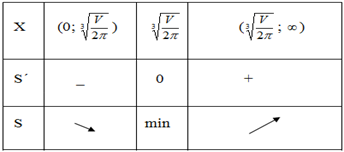
Следовательно, функция в этой точке достигает наименьшего значения.
Таким образом, площадь
полной поверхности цилиндра, имеющего объем V, будет наименьшей при h = 2x = 2 ![]() =
= ![]() , т.е.
когда цилиндр равносторонний.
, т.е.
когда цилиндр равносторонний.
Наименьший расход жести на изготовление консервных банок цилиндрической формы заданной емкости будет достигнут при условии, что диаметр основания и высота банки равны между собой. Полезно обратить внимание на то, что в нашей стране выпускаются ежегодно сотни миллионов банок консервов в жестяной упаковке. Экономия 1% жести на изготовление каждой банки позволит за счет сэкономленного материала дополнительно изготовить несколько миллионов новых банок. Вместе с тем промышленность нередко выпускает консервы в жестяной таре, не обеспечивая наименьший расход материала на изготовление банки. Это обусловлено рядом причин: стремлением минимизации отходов при изготовлении банок, соображениями торговой эстетики, возможностями транспортировки и т.д.
Упражнения:
319) Из всех прямоугольников с периметром р найти прямоугольник наибольшей площади.
320) Из всех прямоугольников, площадь которых равна 9 см2, найти прямоугольник с наименьшим периметром.
321) Из квадратного листа картона со стороной а нужно сделать открытую сверху коробку прямоугольной формы, вырезав по краям квадраты и загнув образовавшиеся края. Какой должна быть высота коробки, чтобы её объём был наибольшим?
322) Равнобедренные треугольники описаны около квадрата со стороной а так, что одна сторона квадрата лежит на основании треугольника. Найти такое значение х, при котором площадь треугольника наименьшая.
323) Найти на параболе у = х2 точку, ближайшую к точке А(2;0,5).
324) Из трёх досок одинаковой ширины скрлачитвается жёлоб. При каком угде наклона боковых стенок к основанию площадь поперечного сечения жёлоба будет наибольшей?
325) Из всех прямоугольников, вписанных в полукруг радиуса R так, что одна сторона прямоугольника лежит на диаметре полукруга, выбран тот, у которого наибольшая площадь. Найти эту площадь.
326) Найти наибольший из объёмов всех пирамид, у каждой из которых высота равна 12, а основанием является прямоугольный треугольник с гипотенузой 4.
327) Периметр основания прямоугольного параллелепипеда 8 м, а высота 3 м. какой длины должны быть стороны основания, чтобы объём параллелепипеда будет наибольшим?
328) Из всех равнобедренных треугольников с пениметром р найти треугольник с наибольшей площадью.
329) Из всех прямоугольных параллелепипедов, у которых в основании лежит квадрат и площадь полной поверхности 600 см2, найти параллелепипед наибольшего объёма.
330) Открытый кузов грузового автомобиля имеет вид прямоугольного параллелепипеда с площадью поверхности 2S. Каковы должны быть длина и ширина кузова, чтобы его объём был наибольшим, а отношение длины к ширине равнялось 5:2.
331) Отраслевая функция спроса на продукт имеет вид P=20–0,5Q. Этот
продукт производится одной фирмой с функцией общих затрат
ТС = 0,04Q3 –1,94Q2 + 32,96Q . При каком выпуске прибыль фирмы максимальна? Какова величина этой прибыли?
332) Пусть: V
–количество единиц выпускаемой продукции;
L(V)–доход
предприятия;
C(V)
– затраты предприятия;
П(V) = L(V)-C(V)
–прибыль предприятия.
Принято решение: ввести дополнительный налог r
на каждую единицу продукции. Каким должен быть налог, чтобы доход R
= r V1,
полученный от дополнительного налога, был максимальным?
333) Пусть: L(V)
= -2V2 +
6V, С(V)
= V2 +
3V +
2.
Найдите величину дополнительного налога r,
при котором доход от его введения максимален.
334) Пусть цена единицы товара равна С условных единиц, количество единиц реализованного товара равно V. Доход от реализации товара L=CV.
Предельный доход равен L '(V). Функция спроса С=8-V. Тогда L=(8-V)V=8V-V ‘. При этом С>0,V≥0, 0≤V<8.
335) Зависимость между издержками производства С и объемом продукции Q выражается функцией С = 30 Q - 0,08 Q3. Определить средние и предельные издержки при объеме продукции: а) 2=5 ед., б) 2=10ед.
336) Функции долговременного спроса D и предложения 5 от цены р
на мировом рынке нефти имеют, соответственно, вид D = 30-0,9p, 5=16+1,2р.
Найти эластичность спроса в точке равновесной цены. Как изменятся
равновесная цена и эластичность спроса при уменьшении предложения нефти на рынке на 25 %.
§2.Приложение дифференциала к приближённым вычислениям.
Приближенные вычисления с применением дифференциала функции основаны на приближенной замене приращения функции в точке на ее дифференциал:
![]() у
=
dy. Абсолютная
погрешность от такой замены при х
у
=
dy. Абсолютная
погрешность от такой замены при х![]() 0 бесконечно малой более
высокого порядка по сравнению с
0 бесконечно малой более
высокого порядка по сравнению с ![]() х. Подставляя
в это приближенное соотношение формулу и выражение для
х. Подставляя
в это приближенное соотношение формулу и выражение для ![]() у,
получаем:
у,
получаем:
f(x
+ ![]()
Пример.
Вычислить приближенное значение корня ![]() .
.
Решение.
Рассмотрим
функцию f (х)
= ![]() в окрестности точки х 0
= 1.
в окрестности точки х 0
= 1.
Поскольку производная этой функции вычисляется по формуле
f'(x)
= ![]() , то, принимая
, то, принимая ![]() х =
0,07, получаем из формулы:
х =
0,07, получаем из формулы:
![]() f(1
+ 0,07) = f(1) +
f(1
+ 0,07) = f(1) + ![]() (1) 0,07 = 1 + 0,5
(1) 0,07 = 1 + 0,5![]() 0,07
= 1,035.
0,07
= 1,035.
Упражнения. Вычислить значения выражений:
337)
Найти приближённое значение выражения у = х2 при х = 2 и ![]() х= 0,01.
х= 0,01.
338) С помощью дифференциалов найти приближённое значение выражения:
а)![]() б)
б)![]() в)
в)![]() г)
г)![]() д)
д)![]()
е)![]() ж)
у = ех, в точке х0 = 0,5 з) у = х2 – х + 1, в
точке х0 = 3,01.
ж)
у = ех, в точке х0 = 0,5 з) у = х2 – х + 1, в
точке х0 = 3,01.
Литература:
1.Ермаков В.И. Общий курс высшей математики для экономистов, Ермаков В.И. , М,2008, 656 стр.
ISBN 5-06-003940-4 Настоящее пособие 5-е изд. — 2002 г. — 495 стр.
4. Рудник А.Е., Сборник задач по элементарной математике для техникумов, Рудник А.Е., Клюева Л.А., Мосолова М.С., Наука, 1974, 321 стр.
5. Богомолов Н.В.,
Практические занятия по математике, Богомолов Н.В., Высшая
школа, 6-е, стереотипное , 2003, 212 стр.
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Калязинский колледж им. Н.М. Полежаева
УЧЕБНО–МЕТОДИЧЕСКОЕ ПОСОБИЕ
«МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО НАПИСАНИЮ ПРАКТИЧЕСКИХ РАБОТ»
|
ЕН.01.Математика190604 Техническое обслуживание и ремонт автомобильного транспорта 151001 Технология машиностроения 080114 «Экономика и бухгалтерский учет (по отраслям)»
|
|
|
|
|
|
|
|
Калязин 2013 |
|
|
|
|
|
|
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Методические рекомендации по написанию практических работ предназначены для преподавателей математики и студентов 2 курса, обучающихся по специальностям 190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)». Рекомендации составлены для методического обеспечения учебного процесса; в соответствии с федеральными государственными образовательными стандартами СПО по специальностям 190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения,080114 «Экономика и бухгалтерский учет (по отраслям)»; направлены на приобретение практических навыков при решении прикладных задач и для оказания помощи студентам при подготовке к практическим работам. Методические рекомендации могут быть использованы для подготовки студентов при дистанционной форме обучения.
|
Методические рекомендации по написанию практических работ по предмету МАТЕМАТИКА, 2 курс 190604, 151001/ Старикова Наталия Валерьевна.
СОДЕРЖАНИЕ:
|
|
Методические рекомендации по выполнению практической работы № 1.
«Вычисление пределов последовательностей.
Вычисление пределов функций».
Приведём
несколько примеров вычисления пределов последовательностей.
1.Вычисление пределов последовательностей
вида: ![]()
Что бы вычислить пределы данного вида, необходимо разделить числитель и знаменатель дроби на наибольшую степень дроби.
1) ![]()
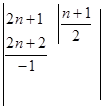 =
=![]() , т.к.
, т.к. ![]() - бесконечно малая и
- бесконечно малая и ![]()
2) ![]() (делим числитель и знаменатель на максимальную степень
(делим числитель и знаменатель на максимальную степень ![]()
![]() )
=
)
= 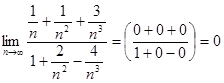
3) ![]()
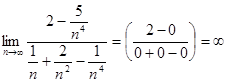
4) ![]()
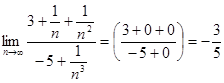
5) ![]() = (вынесем х2 за скобку под корнем и затем
вынесем х за знак корня) =
= (вынесем х2 за скобку под корнем и затем
вынесем х за знак корня) = 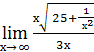 = (сократим на х числитель и знаменатель) =
= (сократим на х числитель и знаменатель) = 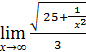 =
= ![]() .
.
Для быстрого нахождения пределов данного вида, можно использовать следующие выводы.
Выводы:
1. Если степень числителя выше степени
знаменателя, то предел равен ![]() .
.
2. Если степень знаменателя выше степени числителя, то предел равен нулю.
3. Если старшие степени числителя и знаменателя равны, то предел равен отношению коэффициентов при старших степенях.
2.Вычисление
пределов последовательности вида: ![]() .
.
Что бы вычислить пределы
данного вида, необходимо воспользоваться формулой второго замечательного
предела: ![]() е, то есть во всех пределах необходимо выделить единицы и
знак плюс, знаменатель дроби и показатель степени могут быть любыми, но равными
между собой.
е, то есть во всех пределах необходимо выделить единицы и
знак плюс, знаменатель дроби и показатель степени могут быть любыми, но равными
между собой.
1) ![]() (делим числитель и знаменатель на 3) =
(делим числитель и знаменатель на 3) =
= 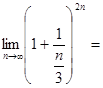 ( сравниваем с
формулой: показатель равен знаменателю дроби, уравниваем; затем используем
свойства степеней для того, чтобы степень выражения не изменялась) =
( сравниваем с
формулой: показатель равен знаменателю дроби, уравниваем; затем используем
свойства степеней для того, чтобы степень выражения не изменялась) = 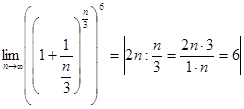 =
= ![]() е
е![]()
2) 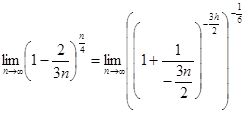
![]() е
е![]() =
= ![]()
3)![]()
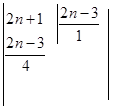 =
= 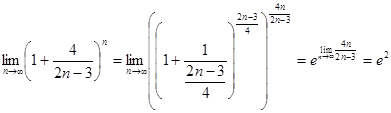
3.Вычисление пределов вида: ![]()
Чтобы вычислить пределы данного вида, необходимо умножить числитель и знаменатель дроби на выражение, сопряжённое числителю.
1) ![]() [
[![]() ] = (умножаем числитель и знаменатель
на выражение сопряжённое числителю) =
] = (умножаем числитель и знаменатель
на выражение сопряжённое числителю) = ![]()
=![]()
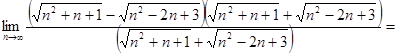 ( в числителе применяем формулу разности квадратов, в
знаменателе n2 вынесем за скобку под каждым из корней, затем n вынесем за скобку, потом за знак
корня) =
( в числителе применяем формулу разности квадратов, в
знаменателе n2 вынесем за скобку под каждым из корней, затем n вынесем за скобку, потом за знак
корня) = 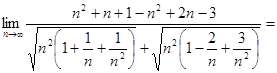
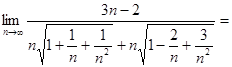
(получили вид
неопределённости ![]() ) =
) =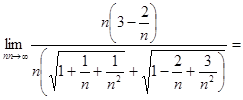
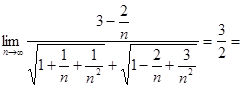 1,5.
1,5.
4.Вычисление пределов функций.
1) Предел многочлена.
![]()
То есть, достаточно подставить вместо х единицу, и предел найден.
2) Предел отношения двух многочленов.
а ![]()
б.![]()
в. Чтобы найти пределы
данного типа, необходимо числитель и знаменатель дроби разделить на (х – а), а
– это то число, к которому стремится х.![]() (числитель разложили на множители
по формуле разности квадратов, затем сократили дробь на одинаковый множитель).
(числитель разложили на множители
по формуле разности квадратов, затем сократили дробь на одинаковый множитель).
г. Вычисление пределов некоторых иррациональных функций:
![]() (умножаем числитель и знаменатель на выражение, сопряжённое
знаменателю) =
(умножаем числитель и знаменатель на выражение, сопряжённое
знаменателю) = ![]()
= 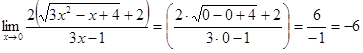
3) Решение примеров на
первый замечательный предел: ![]() .
.
1) ![]() (умножим числитель и знаменатель на 3) =
(умножим числитель и знаменатель на 3) =
= ![]()
2) ![]() (cos0 = 1)
(cos0 = 1)
3) ![]() - используем формулы понижения
степени =
- используем формулы понижения
степени = 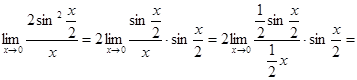
= 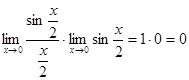
4) ![]() (умножим числитель и знаменатель на x) =
(умножим числитель и знаменатель на x) = ![]()
= 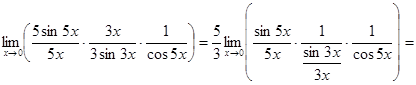
![]()
Методические рекомендации по выполнению практической работы № 2.
«Вычисление производных элементарных функций.
Производная сложной функции»
СПРАВОЧНЫЙ МАТЕРИАЛ. ФОРМУЛЫ ПРОИЗВОДНЫХ.
|
1. С/ = 0 2. (кх)/ = к 3. (кх+в)/ = к 4. (U+V)/ = U/+V/ 5. (U-V)/ = U/-V/ 6. (UV)/ =U/V+V /U (кU)/ = к(U)/ 7.
( 8.
9.(sinx)/ = cosx 10. (cosx)/ = -sinx 11.
(tgx)/ =
|
12.
(ctgx)/ = - 13.(logax)/
= 14.(lnx)/
= 15.(lgx)/
= 16.( 17.(ах)/ = axlna 18.(arctgx)/
= 19.
(arcctgx)/ = - 20.
(arcsinx)/ = 21.(arccosx)/
= - |
Правила дифференцирования.
Производная суммы и разности.
Пусть даны функции f(x) и g(x), производные которых нам известны. Тогда можно найти производную суммы и разности этих функций: (f + g)/= f / + g / (f − g)/ = f / − g /
Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)/ = f /+ g / + h /. Строго говоря, в алгебре не существует понятия «вычитание». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.
Примеры. Найти производные функций: f(x) = x2 + sin x; g(x) = x4 + 2x2 − 3.
Решение.
1. Функция f(x) — это сумма двух элементарных функций, поэтому: f /(x) = (x2 + sin x)/ = (x2)/ + (sin x)/ = 2x + cos x;
2. Аналогично рассуждаем для функции g(x). Только там уже три слагаемых (с точки зрения алгебры): g /(x) = (x4 + 2x2 − 3)/ = (x4 + 2x2 + (−3))/ = (x4)/ + (2x2)/ + (−3)/ = 4x3 + 4x + 0 = 4x · (x2 + 1).
Производная произведения.
(f · g) / = f / · g + f · g /
Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.
Примеры. Найти производные функций: f(x) = x3 · cos x; g(x) = (x2 + 7x − 7) · ex.
Решение.
1. Функция f(x) представляет собой произведение двух элементарных функций, поэтому: f /(x) = (x3 · cos x)/ = (x3)/ · cos x + x3 · (cos x)/ = 3x2 · cos x + x3 · (− sin x) = x2 · (3cos x − x · sin x)
2.У функции g(x) первый множитель сложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:
g /(x) = ((x2 + 7x − 7) · ex)/ = (x2 + 7x − 7)/ · ex + (x2 + 7x − 7) · (ex)/ = (2x + 7) · ex + (x2 + 7x − 7) · ex = ex · (2x + 7 + x2 + 7x −7) = (x2 + 9x) · ex = x(x + 9) · ex.
Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.
Производная частного.
![]()
Примеры. Найти производные функций:
![]()
Решение.
1.В числителе и знаменателе каждой дроби стоят элементарные функции, поэтому все, что нам нужно — это формула производной частного:
![]()
2.![]()
По традиции, разложим числитель на множители — это значительно упростит ответ:
![]()
2.Производная сложной функции.
Сложная функция — это не обязательно формула длиной в полкилометра. Например, достаточно взять функцию f(x) = sin x и заменить переменную x, скажем, на x2 + ln x. Получится f(x) = sin (x2 + ln x) — это и есть сложная функция. У нее тоже есть производная, однако найти ее по правилам, рассмотренным выше, не получится. Как быть? В таких случаях помогает замена переменной и формула производной сложной функции: f /(x) = f /(t) · t /, если x заменяется на t(x).
Как правило, с пониманием этой формулы дело обстоит еще более печально, чем с производной частного. Поэтому ее тоже лучше объяснить на конкретных примерах, с подробным описанием каждого шага.
Примеры. Найти производные функций: f(x) = e2x + 3; g(x) = sin (x2 + ln x)
Решение.
1.Заметим, что если в функции f(x) вместо выражения 2x + 3 будет просто x, то получится элементарная функция f(x) = ex. Поэтому делаем замену: пусть 2x + 3 = t, f(x) = f(t) = et. Ищем производную сложной функции по формуле: f /(x) = f /(t) · t / = (et)/ · t / = et · t /.А теперь — внимание! Выполняем обратную замену: t = 2x + 3. Получим:
f ’(x) = et · t ’ = e2x + 3 · (2x + 3)’ = e2x + 3 · 2 = 2 · e2x + 3
2.Теперь разберемся с функцией g(x). Очевидно, надо заменить x2 + ln x = t. Имеем: g /(x) = g /(t) · t / = (sin t)/ · t / = cos t · t /.Обратная замена: t = x2 + ln x. Тогда: g /(x) = cos (x2 + ln x) · (x2 + ln x)/ = cos (x2 + ln x) · (2x + 1/x).
Таким образом, вычисление производной сводится к избавлению от этих самых штрихов по правилам, рассмотренным выше. В качестве последнего примера вернемся к производной степени с рациональным показателем:
(xn)/ = n · xn − 1
Немногие знают, что в роли n вполне может выступать дробное число. Например, корень — это x0,5. А что, если под корнем будет стоять что-нибудь навороченное? Снова получится сложная функция — такие конструкции любят давать на контрольных работах и экзаменах.
Примеры. Найти производную функции:
![]()
Решение. Для начала перепишем корень в виде степени с рациональным показателем: f(x) = (x2 + 8x − 7)0,5. Теперь делаем замену: пусть x2 + 8x − 7 = t. Находим производную по формуле: f /(x) = f /(t) · t / = (t0,5)/ · t / = 0,5 · t−0,5 · t /.
Делаем обратную замену: t = x2 + 8x − 7. Имеем:
|
f ’(x) = 0,5 · (x2 + 8x − 7)−0,5 · (x2 + 8x − 7)’ = 0,5 · (2x + 8) · (x2 + 8x − 7)−0,5. Наконец, возвращаемся к корням:
|
||
|
|
|
|
Методические рекомендации по выполнению практической работы № 3.
«Геометрический смысл производной. Физический смысл производной»
1. Геометрический смысл производной.
Значение производной в точке x0 равно угловому коэффициенту касательной к графику функции y = f(x) в этой точке: к = у/(х0).
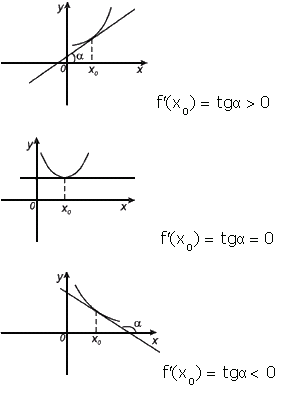
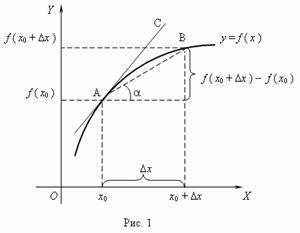
Видим, что для любых двух точек A и B графика функции:
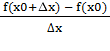 = tg
= tg![]() , где
, где ![]() - угол наклона секущей AB.
- угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то ![]() x неограниченно уменьшается и
приближается к 0, а секущая АВ приближается к касательной АС. Следовательно,
предел разностного отношения равен угловому коэффициенту касательной в точке A.
x неограниченно уменьшается и
приближается к 0, а секущая АВ приближается к касательной АС. Следовательно,
предел разностного отношения равен угловому коэффициенту касательной в точке A.
Отсюда следует: Значение производной функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
|
Справочный материал. Геометрический смысл производной. к = tg |
|
|
Уравнение касательной y-y0 = f'(x0)(x-x0) |
|
|
Уравнение нормали y-y0
= - |
|
|
Условия: параллельности прямых: к1 = к2 перпендикулярности прямых: к1к2 = -1 |
|
Пример 1. На параболе у = х2 - 2х – 8 найти точку М, в которой касательная к ней параллельна прямой 4х + у + 4 = 0.
Решение. Определим угловой коэффициент касательной к параболе
у = х2 – 2х – 8: k = у' = (х2 - 2х - 8)' = 2х – 2.
Найдем угловой коэффициент прямой 4х + у + 4 = 0: у = -4х – 4, k = -4. Касательная к параболе и данная прямая, по условию, параллельны. Следовательно, их угловые коэффициенты равны, т.е. 2х - 2 = -4; х = -1 – абсцисса точки касания. Ординату точки касания М вычислим из уравнения данной параболы у = х2 – 2х – 8, то есть у(-1) = (-1)2 – 2(-1) – 8 = -5, М(-1;-5).
Ответ: М(-1;-5).
Пример 2. Составить уравнение касательной к графику функции y=x+e-2x, параллельной прямой y = -x.
Решение. Угловой коэффициент касательной равен значению производной в точке касания x0. Так как касательная параллельна прямой y = -x, значит ее угловой коэффициент равен –1.Таким образом, f'(x0) = -1.
Найдём производную функции: f/ = 1 – 2е-2х
Прировнняем производную к -1: 1 – 2е-2х = -1
2е-2х = 2
е-2х = 1
х = 0
Уравнение касательной: у = у(х0) + у/(х0)(х – х0)
Уравнение касательной: y =1-1(x-0) = 1-x
Ответ: y = 1-x.
Пример 3. Для параболы у = х2 – 4х написать уравнение касательной в точке с абсциссой, равной 1.
Решение. Уравнение касательной имеет вид у = у(х0) + у/(х0)(х – х0).
1.Найдём производную функции: у/ = 2х – 4
2. Найдём
значение производной в точке х0 = 1: у/(1) = 2![]() - 4 = -2
- 4 = -2
3. Найдём значение функции в точке х0 = 1: у(1) = 1 – 4 = -3
4. Подставим полученные числа в формулу касательной:
у = -3 + (-2)(х – 1)
у = -3 – 2х + 2
у = -2х – 1
Ответ: уравнение касательной имеет вид у = -2х – 1
2.Физический смысл производной.
V = S'; a = V'= S''
Если материальная точка движется прямолинейно по закону s (t), то производная функции у = s (t0) выражает мгновенную скорость материальной точки в момент времени t0, т.е. v = s' (t0).
Замечание: при решении задач будем считать, что если s' (t0) = 0, то в момент времени t0 точка останавливается.
Пример 1. Материальная точка движется прямолинейно по закону х(t) = 6t2 – 48t + 17 , где x(t) — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9c.
Решение.
1.Найдем производную функции: х(t) = 6t2 – 48t + 17
x| = 12t - 48
2. Найдем значение производной в точке t = 9: x| = 60
Ответ: 60 м/с.
Пример 2. Материальная точка движется прямолинейно по закону x = t2 – 13t + 23 , где x(t) - расстояние от точки отсчета в метрах, t - время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Решение.
Если нам известна скорость точки в некий момент времени, следовательно известно значение производной в точке t0. Найдем производную функции
x = t2 – 13t + 23 , x| = 2t - 13
По условию, скорость точки равна 3 м/с, значит, значение производной в момент времени t0 равно 3. Получаем уравнение:
2t – 13 = 3
2t = 16
t =8
Ответ: 8
Пример 3. Материальная точка
движется прямолинейно по закону x = ![]() t3 – 3t2 – 5t + 3, где x(t) - расстояние от точки отсчета в
метрах, t - время в
секундах, измеренное с начала движения. В какой момент времени (в секундах) ее
скорость была равна 2 м/с?
t3 – 3t2 – 5t + 3, где x(t) - расстояние от точки отсчета в
метрах, t - время в
секундах, измеренное с начала движения. В какой момент времени (в секундах) ее
скорость была равна 2 м/с?
Решение. Найдем производную функции:
x = ![]() t3 – 3t2 – 5t + 3, x| = t2 – 6t -5.
t3 – 3t2 – 5t + 3, x| = t2 – 6t -5.
По условию, скорость точки равна 2 м/с, значит, значение производной в момент времени t0 равно 2. Получаем уравнение: t2 – 6t -5 = 2
Решим его:
t2 – 6t -5 = 2
t2 – 6t -7 = 0
t1 = 7 t2 = -1 – не подходит по смыслу задачи: время не может быть отрицательным.
Ответ: 7
Пример 4. Прямолинейное движение точки совершается по закону:
S = (t3 — 2) м. Определить ускорение в момент t = 10 сек.
Решение.
Ускорение а = V//.
Дифференцируя
функцию S = t3 — 2,
находим V//=
6t. Следовательно,
a = 6t = 6![]() 10 = 60; a = 60 м/сек2.
10 = 60; a = 60 м/сек2.
Пример 5. Если движение неравномерное, то сила F, производящая его, непостоянна, каждому моменту времени t соответствует определенное значение действующей силы F, и сила, таким образом, есть функция времени t, F=f(t).
По закону Ньютона, в каждый момент времени действующая сила F равна произведению массы т на ускорение а, то есть F=ma, или f(t) = ma.
При прямолинейном движении a = V//, поэтому f(t) = m V//.
Зная уравнение прямолинейного движения, можно дифференцированием найти значение действующей силы в каждый момент времени.
Пример
6.
Определить силу, под действием которой материальная точка совершает
прямолинейные колебания по закону S
= А![]() sin(ωt + ω0).
sin(ωt + ω0).
Решение. f(f) = m V//, поэтому находим вторую производную функции:
S
= А![]() sin(ωt + ω0), ds/dt = А
sin(ωt + ω0), ds/dt = А![]() cos(ωt+ω0)
cos(ωt+ω0)![]() ω,
ω,
V//=
- А![]() sin
(ωt
+ ω0)
sin
(ωt
+ ω0)
![]() ω2 =
- sω2 =
- ω2s;
f(t) = - mω2s,
ω2 =
- sω2 =
- ω2s;
f(t) = - mω2s,
то есть рассматриваемые колебания совершаются под действием силы, пропорциональной перемещению s и направленной в противоположную сторону.
Методические рекомендации по выполнению практической работы № 4.
«Нахождение промежутков монотонности и экстремумов функции».
1.Монотонность функции.
Под монотонностью понимают возрастание и убывание функции.
Алгоритм нахождения промежутков монотонности функции.
1.Найти область определения функции.
2.Найти производную функции.
3.Найти корни производной и точки, в которых производная не существует.
4.Наносим полученные точки на область определения функции.
5.Определяем знаки производной в каждом из полученных промежутков.
6.а) Если производная положительна на промежутке (а; в), то функция возрастает на промежутке (а; в).
б) Если производная отрицательна на промежутке (а; в), то функция убывает на промежутке (а; в).
Пример 1: Исследовать на возрастание и убывание функцию: у = х3 – 3х + 2
Решение:
Находим производную: у/ = 3х2
- 3. Производная
обращается в нуль при значениях: 3х2 – 3 = 0
х1 = 1
х2=-1
![]()
Следовательно, функция f(x) возрастает на промежутке (-![]() ;-1)
;-1) ![]() (1;+
(1;+![]() ), функция убывает на промежутке (-1;1).
), функция убывает на промежутке (-1;1).
Пример 2. Найти промежутки возрастания и убывания функции:
у = хе-3х
Решение: Найдем производную функции: у/ = е-3х - 3хе-3х.
Приравняем производную к нулю: е-3х (1–3х) = 0, откуда х =![]() .
.
При х![]() ,у/
,у/![]() , следовательно, при х
, следовательно, при х![]() , функция возрастает, а при х
, функция возрастает, а при х![]() , у/
, у/![]() следовательно, при х
следовательно, при х![]() , функция убывает.
, функция убывает.
Пример: Найти промежутки монотонности функции y = x4 - x3.
1. D(у ) = R
2. у '(x) = 4x3 - 3x2 = x2 (4x - 3)
3. у '(x) = 0, x = 0 и x = 3/4
4. При х ![]() и при х
и при х![]() производная
положительна, следовательно функция возрастает на этих промежутках; при
производная
положительна, следовательно функция возрастает на этих промежутках; при ![]() х
х ![]() производная
отрицательна, следовательно функция убывает на этом промежутке.
производная
отрицательна, следовательно функция убывает на этом промежутке.
Пример 3. Найти интервалы
возрастания функции: у = ![]()
Найдите интервалы, принадлежащие области определения функции, на которых ее производная положительна.
Решение: Область определения функции: любое действительное число, кроме 1 и -1.
Найдем производную и
исследуем ее знак: у/=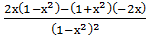 =
=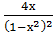
С учетом области
определения интервалы возрастания: (0;1)![]()
Ответ: (0;1)![]()
2.Экстремумы функции.
Алгоритм нахождения экстремумов функции.
|
1.Найти область определения функции. 2.Найти производную функции. 3.Найти корни производной и точки, в которых производная не существует. 4.Наносим полученные точки на область определения функции. 5.Определяем знаки производной в каждом из полученных промежутков. 6.а) Если производная положительна на промежутке (а; в), то функция возрастает на промежутке (а; в). б) Если производная отрицательна на промежутке (а; в), то функция убывает на промежутке (а; в). |
|
|
7.Если при переходе через точку х0 производная изменяет свой знак с «-» на «+», то точка х0 – точка минимума. Если при переходе через точку х0 производная изменяет свой знак с «+» на «-«, то х0 – точка максимума. 8.Чтобы найти экстремумы, необходимо найти значения функции в точках экстремумов.
Пример 1. Исследовать функцию на экстремум: у = х2 – 4х. 1.Находим область определения: любое действительное число. 2. Находим производную функции: у/=2х – 4 3. Находим корни производной: 2х – 4 = 0, 2х = 4, х = 2. 4.
Определяем знаки производной при х при
х Ответ: уmin(2) = -4. Пример 2. Найдите точку максимума функции на отрезке [−10; −1]:
Найдем производную:
Поскольку это дробно-рациональная функция, приравниваем к нулю числитель: x2 −25=0; x1 = 5; x2 = −5. Получили два корня. Теперь приравниваем к нулю знаменатель: x2 =0; Получили x = 0 — корень второй кратности. При переходе через него знак производной не меняется. Отмечаем точки x =−5; x =0; x = 5 на координатной прямой, а затем расставить знаки и границы.
Очевидно, что внутри отрезка останется лишь одна точка x = −5,в которой знак производной меняется с плюса на минус. Это и есть точка максимума. Ответ: -5 Пример
3.
Исследовать на экстремум функцию: у = 1.Область определения функции: любое числор, кроме х = 2. 2. Найдём
производную функции: у/ = 3. Находим корни производной и точки, в которой производная не существует: корней нет, так как числитель не равен нулю. Производная не существует, когда знаменатель равен нулю, следовательно х1,2 = 2. 4.Производная имеет знак минус и правее 2, и левее 2. Имеем, что производная не меняет свой знак при переходе через критические точки. Ответ: функцуия экстремумов не имеет.
|
Методические рекомендации по выполнению практической работы № 5.
«Вторая производная. Приложение второй производной к исследованию функции».
1.Понятие второй производной. Механический смысл второй производной.
|
Если функция производную, которую называют производной второго порядка функции
Механический смысл второй производной. Если точка движется
прямолинейно и задан закон ее движения Замечание. Ускорение
материального тела равно первой производной от скорости, то есть: Пример 1. Материальтная точка движется по закону S(t) = 3t3 + 4t + 8, где S – измеряется вметрах, а t – в секундах. Найти значение ускорения через 2 секунды от начала движения. Решение: а = S// 1.Найдём первую производную: S/ = 9t2 + 4 2. Найдём вторую производную, то есть ускорение а = S// = 18t a(2) = 18 Ответ: |
|
Пример 2. Материальная точка движется по закону ![]() , где
, где ![]() измеряется в метрах, а
измеряется в метрах, а ![]() - в секундах. Найти значение
- в секундах. Найти значение ![]() , при
котором ускорение точки равно 12.
, при
котором ускорение точки равно 12.
Решение: Найдем ускорение материальной точки:
![]()
![]()
![]()
Искомое время ![]() найдем из уравнения:
найдем из уравнения:
![]()
Ответ. ![]()
2.Выпуклость графика функции.
Алгоритм нахождения промежутков выпуклости функции. Точки перегиба функции.
1.Найти область определения функции.
2.Найти производную функции.
3. Найти вторую производную функции
3.Найти корни второй производной и точки, в которых вторая производная не существует.
4.Наносим полученные точки на область определения функции.
5.Определяем знаки второй производной в каждом из полученных промежутков.
6.а) Если вторая производная положительна на промежутке (а; в), то график функции имеет выпуклость вниз на промежутке (а; в).
б) Если вторая производная отрицательна на промежутке (а; в), то график функции имеет выпуклость вверх на промежутке (а; в).
7. Точки, отделяющие выпуклую часть от вогнутой – точки перегиба. Найти значения функции в точках перегиба.
Пример 1.Установить интервалы выпуклости и вогнутости кривой y = 2 – x2.
Решение:
Найдем y '' и определим, где вторая производная положительна и где отрицательна. y' = –2x, y'' = –2 < 0 на промежутке (–∞; +∞), следовательно, функция всюду выпукла.
Пример 2. Определить промежутки выпуклости функции y = ex.
Решение: Так как y'' = ex > 0 при любых x, то кривая всюду вогнута.
Пример 3. Найти интервалы
выпуклости функции у = ![]() -
- ![]() + 3х + 1.
+ 3х + 1.
Решение. Найдем вторую производную заданной функции:
![]()
Находим точки, в
которых вторая производная равна нулю, для этого решаем уравнение ![]() :
:
![]()
Исследуем знак второй производной слева и справа от полученной точки:
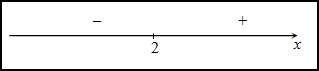
Так как на промежутке ![]() вторая производная
вторая производная ![]() , то на этом
промежутке функция
, то на этом
промежутке функция ![]() выпукла; в
силу того, что на промежутке
выпукла; в
силу того, что на промежутке ![]() вторая производная
вторая производная ![]() - функция вогнута. Так как при
переходе через точку
- функция вогнута. Так как при
переходе через точку ![]() вторая производная сменила знак, то
эта точка является точкой перегиба графика функции. Найдём ординату точки: у(2)
= 4/3 – 4 + 6 + 1 = 4
вторая производная сменила знак, то
эта точка является точкой перегиба графика функции. Найдём ординату точки: у(2)
= 4/3 – 4 + 6 + 1 = 4![]()
Ответ: На промежутке ![]() функция выпукла, на промежутке
функция выпукла, на промежутке ![]() функция вогнута. А(2; 4
функция вогнута. А(2; 4![]() ) - точка перегиба
графика функции.
) - точка перегиба
графика функции.
СПРАВОЧНЫЙ МАТЕРИАЛ.
Физический смысл производной.
V = S' a = V'= S''.
ФОРМУЛЫ ПРОИЗВОДНЫХ.
|
1. С/ = 0 2. (кх)/ = к 3. (кх+в)/ = к 4. (U+V)/ = U/+V/ 5. (U-V)/ = U/-V/ 6. (UV)/ =U/V+V /U (кU)/ = к(U)/ 7.
( 8.
9.(sinx)/ = cosx 10. (cosx)/ = -sinx 11.
(tgx)/ =
|
12.
(ctgx)/ = - 13.(logа
x)/ = 14.(lnx)/
= 15.(lgx)/
= 16.( 17.(ах)/ = axlna 18.(arctgx)/
= 19.
(arcctgx)/ = - 20.
(arcsinx)/ = 21.(arccosx)/
= -
Методические р |
Методические рекомендации по выполнению практической работы № 6.
«Нахождение наибольшего и наименьшего значения функции».
Алгоритм нахождения наибольшего и наименьшего значений функции.
1.Найти производную функции.
2.Найти точки, в которых производная равна нулю или не существует.
3.Проверить, какие из точек принадлежат данной области определения.
4.Найти значения функции в точках, принадлежащих области определения
и на концах отрезка.
5.Из полученных результатов выбрать наибольшее и наименьшее.
Пример 1. Найти наибольшее и наименьшее значения функции:
у = -3х² + 4х - 8, если хє[0;1]
1.Найдём первую призводную: у/= -6х + 4
2.Найдём корни первой производной: –6х + 4 = 0, -6х = 4, х=2/3 є[0;1]
3. Найдём значения функции на концах отрезка и в точке, которая принадлежит данному отрезку:
f (0) = -8
f (![]() ) = - 6
) = - 6![]()
f (1) = -7
Ответ: унаиб(![]() ) = - 6
) = - 6![]() : унаим(0)=
-8.
: унаим(0)=
-8.
Пример 2. Найти наибольшее и наименьшее значения функции:
у = ![]() , х
, х![]()
1.Найдём производную: у/ = ![]() = -
= - ![]()
2.Находим корни производной и точки, в которых она не смуществует:
-х=0 25 - х² = 0
х1=0 є[-4;4] х² = 25
х2 = 5 є[-4;4]
х3 = -5 є[-4;4]
3.Найдём значения функции на концах отрезка и в точках, которые принадлежат отрезку [-4;4]:
¦(0) = 5 – наибольшее значение функции на отрезке
¦(-4) = ![]() = 3 – наименьшее
значение функции
= 3 – наименьшее
значение функции
¦(4) =3 - наименьшее значение функции
Ответ: унаиб.(0) = 5; Унаим.(-4) = 3, унаим.(4) = 3.
Методические рекомендации по выполнению практической работы № 7.
«Нахождение неопределённых интегралов».
Справочный материал.
|
2.
6. 7. 8. 9. 10.
|
11.
16. 17. 18.
|
1.Вычисление неопределённых интегралов.
Примеры. Найти интегралы:
1.![]() 2
+ 4х – 6) dx = x3
+ 2x2 – 6x
+ C
2
+ 4х – 6) dx = x3
+ 2x2 – 6x
+ C
2.![]() ; 3.
; 3.![]() ; 4.
; 4.![]() .
.
Решение.
2. ![]()
![]() .
.
3.![]()
![]() .
.
4. Предварительно числитель подынтегральной функции почленно разделим на знаменатель, затем последовательно применим формулы:
![]()
![]() .
.
5.![]() ;
;
6.![]() ;
;
6.![]() ;
;
Всякая формула интегрирования
сохраняет вид при подстановке вместо независимой переменной любой
дифференцируемой функции от неё, т. е. если![]() , то и
, то и ![]() , где
, где ![]() – любая дифференцируемая
функция от х.
– любая дифференцируемая
функция от х.
Это правило очень важно. Основная таблица интегралов в силу этого правила оказывается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой дифференцируемой функцией её. Покажем на примерах как пользоваться этим методом.
Примеры:
1. .
.
2. .
.
3.![]()
4.
5.
6.
7.![]()
8.
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Калязинский колледж им. Н.М. Полежаева
190604 Техническое обслуживание и ремонт автомобильного транспорта
151001 Технология машиностроения
080114 «Экономика и бухгалтерский учет (по отраслям)»
Калязин
2013 год
Фонд оценочных средств представлен уровневой моделью контрольно-оценочных средств в условиях балльно-рейтинговой системы оценивания.
Фонд оценочных средств: «Математика» 2 курс 190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)»
Старикова Наталия Валерьевна.
Паспорт фонда оценочных средств по дисциплине
МАТЕМАТИКА 2 курс 190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)».
|
|
Контролируемые разделы (темы) дисциплины* |
Результаты обучения |
Наименование оценочного средства |
|
|
Освоенные умения |
Усвоенные знания |
|||
|
1 1. |
Раздел 1. «Пределы».
|
Вычисление пределов
последовательностей видов: Вычисление пределов функций: на бесконечности; в точке; первый замечательный предел.
|
Определение
и правила вычисления пределов последовательностей видов: Определение и правила вычислений пределов функций: на бесконечности; в точке; первый замечательный предел.
|
1.Практическая работа№1 2. Тесты (КИМы для подготовки промежуточной аттестации). 3.Тесты (КИМы для проведения промежуточной аттестации). |
|
2 |
Раздел 2. «Основы дифференциального исчисления».
|
Вычисление производной функции; сложной функции. Решение задач на нахождение уравнений касательной и нормали; на нахождение скорости по указанному пути. |
Формулировка правил дифференцирования, перечисление производных основных элементарных функций, формулировки геометрического и физического смысла производной. |
1.Практическая работа №3 2.Практическая работа №3 2. Тесты (КИМы для подготовки промежуточной аттестации). 3.Тесты (КИМы для проведения промежуточной аттестации) |
|
3 3. |
Раздел 3. «Приложение производной к исследованию функций». |
Нахождение промежутков монотонности, экстремумов функции; промежутков выпуклости и точек перегиба; нахождение наибольшего и наименьшего значений функции на отрезке. Приёмы решения прикладных задач. |
Алгоритмы нахождения промежутков монотонности, экстремумов функции; промежутков выпуклости и точек перегиба; нахождение наибольшего и наименьшего значений функции. План построения графика функции с помощью производной. Приёмы решения прикладных задач. |
1.Практическая работа №4 2.Практическая работа №5 3.Практическая работа №6 4. Тесты (КИМы для подготовки промежуточной аттестации). 5.Тесты (КИМы для проведения промежуточной аттестации) 6.Рубежный контроль. |
|
4 4. |
Раздел 4. Дифференциал. Первообразная. Интеграл.
|
Нахождение неопределённых интегралов методами непосредственного интегрирования; методом подстановки. Нахождение площадей плоских фигур при помощи определённого интеграла. Нахождение пути при полмощи определённого интеграла. |
Перечисление табличных интегралов, методов интегрирования, приложения определенного интеграла к вычислению площадей плоских фигур; решению прикладных задач по нахождению пути. |
1.Практическая работа №7 2. Тесты (КИМы для подготовки промежуточной аттестации). 3.Тесты (КИМы для проведения промежуточной аттестации
|
|
5 5. |
Раздел 5. Численное дифференцирование. Численное Интегрирование. |
Нахождение определённого интеграла методами численных методов вычисления. Составлять интерполяционные многочлены и находить их производную. |
Правила численного интегрирования при помощи методов прямоугольников, трапеций и парабол. Формулы дифференцирования интерполяционных многочленов. |
Тесты (КИМы для подготовки промежуточной аттестации).
|
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Калязинский колледж им. Н.М. Полежаева
УЧЕБНО-ПРАКТИЧЕСКОЕ ПОСОБИЕ
«КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ДЛЯ ПОДГОТОВКИ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ»
190604 Техническое обслуживание и ремонт автомобильного транспорта
151001 Технология машиностроения
080114 «Экономика и бухгалтерский учет (по отраслям)»
Калязин
2013 год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Контрольно-измерительные материалы предназначены для преподавателей математики и студентов 2 курса, обучающихся по 190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)». Материалы предназначены для методического обеспечения учебного процесса; составлены в соответствии федеральными государственными образовательными стандартами СПО по специальностям190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)». Материалы направлены на приобретение практических навыков при решении прикладных задач и для подготовки студентов к промежуточной аттестации. КИМы могут быть использованы для самостоятельной работы студентов при дистанционной форме обучения.
Учебно-практическое пособие «Контрольно–измерительные материалы для подготовки к промежуточной аттестации» «Математика» 2 курс
/ Старикова Наталия Валерьевна.
Описание.
КИМы содержат разноуровневые материалы: ознакомительного, репродуктивного и продуктивного уровней.
Задания ознакомительного уровня – задания закрытого типа, то есть из четырёх возможных: один ответ верный и три неверных ответа. Задания репродуктивного уровня – задания открытого типа, предполагают запись ответа. Задания продуктивного уровня – задания открытого типа, предполагают развёрнутую запись ответа.
Тестирование проводится онлайн через образовательную систему eduhouse.ru. Варианты составляются программой в произвольном порядке, включая 10 заданий ознакомительного уровня, 3 задания репродуктивного уровня и 2 задания продуктивного уровня. Время проведения 90 минут.
Критерии оценки:
«7» баллов выставляется за выполнение 100 % заданий, выданных преподавателем; умение работать со всеми видами источников, проявив самостоятельность и знания межпредметного характера; применение учебной дисциплины в жизни.
«5» баллов выставляется за выполнение не менее 80 % заданий, выданных преподавателем, без существенных ошибок: в его ответе содержатся недочеты или одна негрубая ошибка; при ответе на поставленные вопросы имеются незначительные замечания и поправки со стороны преподавателя. Обучающийся умеет самостоятельно добывать знания, пользуясь различны-ми источниками, имеет развитые практические умения.
«3» балла выставляется студенту за выполнение 60% заданий или выполнение всех заданий с несколькими существенными ошибками; при ответе на поставленные вопросы преподаватель оказывал ему значительную помощь в виде наводящих вопросов. Обучающийся знает только основные принципы, умеет добывать знания лишь из основных источников, имеет частично сформированные знания и умения.
«2» баллов выставляется студенту за выплнение 50% заданий, его ответы содержат более двух грубых ошибок; при ответе на поставленные вопросы преподаватель оказывал ему постоянную помощь. Обучающийся не умеет самостоятельно работать с источниками, не знает принципов учебной дисциплины, у него не сформированы знания и умения.
.
«0» баллов выставляется студенту за выполнение менее чем 50% заданий, его ответ содержит более двух грубых ошибок; при ответе на поставленные вопросы преподаватель оказывал ему постоянную помощь. Обучающийся не умеет самостоятельно работать с источниками, не знает принципов учебной дисциплины, у него не сформированы знания и умения.
Для того, что бы работа была выполненной, необходимо набрать 3 балла.
Контрольно-измерительные материалы
для подготовки промежуточной аттестации.
Тема: Пределы. Производная и ее приложения.
Ознакомительный уровень:
1.Предел отношения приращения функции в точке х к приращению аргумента, когда последнее стремится к нулю называется…
а) производной функции
б) неопределенным интегралом
в) пределом функции
г) первообразной
2.Если материальная точка движется по закону S(t), то первая производная от пути по времени есть…
а) угловой коэффициент
б) ускорение движения
в) скорость в данный момент времени
г) нет верного ответа
3.Геометрический смысл производной состоит в том, что …
а) она равна пределу функции
б) она равна всегда нулю
в) она равна угловому коэффициенту касательной
г) она равна максимальному значению функции
4.Дифференцирование – это…
а) вычисление предела
б) вычисление приращения функции
в) нахождение производной от данной функции
г) составление уравнения нормали
5.Эта
формула выражает 
а) первый замечательный предел;
б) первообразную
в) угловой коэффициент касательной
г) максимальному значению функции
6.Уравнение касательной к данной линии в точке М имеет вид…
а) y - y0 = y/(х) (х-х0)
б) y = y/(х) (х-х0)
в) y - y0 = х - х0
г)
y =
y![]() х
х
7.Производная постоянной величины равна…
а) единице
б) самой постоянной
в) не существует
г) нулю
8.При вычислении производной постоянный множитель можно…
а) возводить в квадрат
б) выносить за знак производной
в) не принимать во внимание
г) принять за нуль
9.Ускорение прямолинейного движения равно…
а) скорости от пути по времени
б) первой производной от пути по времени
в) второй производной от пути по времени
г) нулю
10.Функция возрастает на заданном промежутке, если…
а) первая производная положительна
б) вторая производная положительна
в) первая производная отрицательна
г) первая производная равна нул
11.Найти: 
|
а
|
б |
в |
г |
|
Не существует
|
0 |
2/3 |
0,5 |
12. Найти 
|
а
|
б |
в |
г |
|
1
|
0 |
-1 |
|
13.Найти 
|
а
|
б |
в |
г |
|
Не существует
|
0 |
|
|
14.Найти: 
|
а
|
б |
в |
г |
|
е2
|
е |
|
|
15. Найдите производную функции y = x3 + cosx.
а) y/=3x2 – sin x б) y/=x3 – sin x в) y/=3x2 + sin x г) y/=x3ln3 + sin x
16. Найдите производную функции y=2x – sin x.
а) y/= x2 – cos x б) y/=x2 – sin x в)y/=2 - cos x г) y/= 1 + cos x
17. Найдите производную функции y=2x + 1.
а)y/=![]() б) y/=
б) y/=![]() в) y/=
в) y/=![]() г) y/=
г) y/=![]()
18. Найдите производную функции y= -ex + 3x3.
а) y/=ex + 3x б) y/=-xex + 9x2 в) y/=-ex +9x2 г) y/=-ex-1 +9x3.
19. Найдите производную функции y=e2x – ln(3x – 5)
а) y/=2e2x
- ![]() б)
y/=2e2x
-
б)
y/=2e2x
- ![]() в)
y/=e2x
-
в)
y/=e2x
- ![]()
г) y/=e2x
- ![]()
20. Вторая производная ![]() (x)
функции y(x)=4
(x)
функции y(x)=4![]() -2x
имеет вид
-2x
имеет вид
|
а |
б |
в |
г |
|
4 |
8 |
6 |
7 |
21. Скорость тела определяется по формуле V(t) = 5t3
+ t2. Чему равно ускорение тела в момент времени t 0 =1с?
|
а |
б |
в |
г |
|
16 |
6 |
17 |
34 |
22. Точка движется по закону S(t) = 2t3 - 3t. Чему равно ускорение в момент t 0 =1с?
|
а |
б |
в |
г |
|
15 |
12 |
9 |
3 |
23. Найти промежутки возрастания функции: у = - х3 + 3х.
|
а) (-
|
б) возрастает на D(y) |
в) (-1;1)
|
г) [-1;1] |
Репродуктивный уровень.
24. Найти экстремумы функции: у = х2 + 9.
25.Найти наибольшее и наименьшее значения: у = х2 - 1 на отрезке [-2;1].
26. Найти промежутки выпуклости вниз: у = - х3 + 3х.
27. Материальная точка
движется по закону: S = sinx
(м). Найти ускорение движения точки через ![]() секунды от начала
движения.
секунды от начала
движения.
Ответы:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
а |
в |
в |
в |
а |
а |
г |
б |
в |
а |
в |
г |
г |
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
а |
а |
в |
а |
в |
а |
б |
в |
б |
г |
24. (0;9) 25. унаим(0) = -1; Унаиб(-2) = 3
26. выпукла вниз при х![]() , выпукла вверх при х
, выпукла вверх при х![]()
27.-1
Тема: Неопределённый интеграл.
Определённый интеграл и его приложеия.
Ознакомительный уровень:
28.Функция F называется первообразной для функции f на некотором промежутке, если для всех x из этого промежутка существует производная
F/(х), равная f(х), т.е. F/(х)=f(х) это…
а) формула Ньютона-Лейбница
б) дифференциал функции
в) первообразная для функции f
г) производная в точке
29. Множество первообразных для данной функции f(х) называется…
а) функцией
б) неопределенным интегралом
в) постоянным множителем
г) частной производной
30. Операция нахождения неопределенного интеграла называется…
а) дифференцированием функции
б) преобразованием функции
в) интегрированием функции
г) нет верного ответа
31. Непосредственное интегрирование, метод подстановки, интегрирование по частям это…
а) методы нахождения производной
б) методы интегрирования
в) методы решения задачи Коши
г) все ответы верны
32. Производная от неопределенного интеграла равна…
а) подынтегральной функции
б) постоянной интегрирования
в) переменной интегрирования
г) любой функции
33. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен…
а) произведению интегралов этих функций
б) разности этих функций
в) алгебраической сумме их интегралов
г) интегралу частного этих функций
34. Определенный интеграл вычисляют по формуле…
а)
![]()
![]() f(х)dx=F(a)-F(b)
f(х)dx=F(a)-F(b)
б)
![]()
![]() f(х)dx=F(b)-F(a)
f(х)dx=F(b)-F(a)
в)
![]()
![]() f(х)dx=F(a)+F(b)
f(х)dx=F(a)+F(b)
г) ![]()
![]() f(х)dx=F(a)
f(х)dx=F(a)
35. Определенный интеграл с одинаковыми пределами равен…
а) единице
б) бесконечности
в) нулю
г) указанному пределу
36. При перемене местами верхнего и нижнего пределов интегрирования определенный интеграл…
а) остается прежним
б) меняет знак
в) увеличивается в два раза
г) равен нулю
37. Определенный интеграл используется при вычислении…
а) площадей плоских фигур
б) объемов тел вращения
в) пройденного пути
г) всех перечисленных элементов
38. Формула Ньютона-Лейбница
а)


б)

в)

39. Вычисление пути, пройденного материальной точкой производится по формуле:
а)

б)

в)

г)

40. Если ![]() то
площадь криволинейной трапеции, ограниченной этой линией, двумя прямыми x=a
и x=b
и отрезком оси абсцисс a
≤ x
≤ b, вычисляется по
формуле
то
площадь криволинейной трапеции, ограниченной этой линией, двумя прямыми x=a
и x=b
и отрезком оси абсцисс a
≤ x
≤ b, вычисляется по
формуле
а)

б)

в)

г)

41. Укажите первообразную функции ![]()
а)
![]()
б)

в)
![]()
г)
![]()
42.Определенный интеграл  равен
равен
|
а
|
б |
в |
г |
|
36
|
17 |
|
15 |
43.Площадь криволинейной трапеции, ограниченной линиями y = 4 – x2, y=0 определяется интегралом:
|
а
|
б |
в |
г |
|
|
|
|
|
44. В результате подстановки t
= 3x + 2 интеграл ![]() приводится к виду
приводится к виду
|
а
|
б |
в |
г |
|
|
|
|
|
45.Определенный интеграл ![]() равен:
равен:
|
а
|
б |
в |
г |
|
19 |
18 |
35 |
27
|
46. Множество всех первообразных функции y=5![]() имеет вид:
имеет вид:
|
а
|
б |
в |
г |
|
х5 |
5х5 + С |
х5 + С |
5х3 + С
|
Репродуктивный:
47. Тело движется прямолинейно со скоростью V (t) = (3t2 + 4t + 1) м/с. Вычислить путь, пройденный телом за первые 3 секунды.
48.Тело движется прямолинейно со скоростью V(t) = (t + 6t 2) м/с.
Найти путь, пройденный телом за третью секунду.
Продуктивный:
49. Найти площадь фигур, ограначенных следующими функциями:
у = sinx,
y = 0, x
= 0, x = 2![]() .
.
50. Определить максимальную высоту подъема камня, брошенного вертикально вверх со скоростью (18t - 3t2) м/с.
51. ![]()
52. ![]()
53. 
Ответы:
|
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
|
в |
б |
в |
б |
а |
в |
б |
в |
б |
г |
а |
а |
а |
а |
г |
|
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
|
б |
б |
а |
б |
48 |
40,5 |
4 |
108 |
|
|
|
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Калязинский колледж им. Н.М. Полежаева
УЧЕБНО-ПРАКТИЧЕСКОЕ ПОСОБИЕ
«КОНТРОЛЬНО–ОЦЕНОЧНЫЕ СРЕДСТВА ДЛЯ ПРОВЕДЕНИЯ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ»
ЕН.01. Математика
190604 Техническое обслуживание и ремонт автомобильного транспорта
151001 Технология машиностроения
080114 «Экономика и бухгалтерский учет (по отраслям)»
Калязин
2013
ОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Материалы рекомендованы для преподавателей математики и студентов 2 курса, обучающихся по специальностям 190604, 151001, 080114.
Контрольно-оценочные средства выполнены в форме контрольно-измерительных материалов. Материалы предназначены для методического обеспечения учебного процесса. КОСы составлены в соответствии с федеральными государственными образоватнельными стандартами СПО по специальностям 190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)». Материалы направлены на приобретение практических навыков при решении прикладных задач и для проведения промежуточной аттестации по предмету математика. Материалы могут быть использованы для проведения промежуточной аттестации студентов дистанционной формы обучения.
Учебно-практическое пособие «Контрольно–оценочные средства для проведения промежуточной аттестации: «Математика» 2 курс (151001,080114 и и 190604) / Старикова Наталия Валерьевна.
1.Общие положения.
КОСы содержат разноуровневые материалы: ознакомительного, репродуктивного и продуктивного уровней.
Задания ознакомительного уровня – задания закрытого типа, то есть из четырёх возможных: один верный и три неверных ответа. Задания репродуктивного уровня – задания открытого типа, предполагают запись ответа. Задания продуктивного уровня – задания открытого типа, предполагают развёрнутую запись ответа.
Результатом освоения учебной дисциплины является - умение применять математические методы для решения профессиональных задач; использовать приемы и методы математического синтеза и анализа в различных профессиональных ситуациях. Формой аттестации по учебной дисциплине является дифференцированный зачёт.
Порядок проведения: с использованием электронной образовательной системы eduhouse.ru. Время проведения 90 минут: 30 минут – на выполнение ознакомительтной части зачёта, 60 минут – на выполнение репродуктивнорй и продуктивной части зачёта.
Оборудование: компьютерный класс, ПК, бумага, ручка.
2.Результаты обучения
(освоенные умения, усвоенные знания).
В результате аттестации по учебной дисциплине осуществляется комплексная проверка следующих умений, навыков и знаний.
Показатели оценки результата:
Умения:
v Находить значения пределов последовательнорстей и пределов функций;
v Решать прикладные задачи в области профессиональной деятельности использовать производную для изучения свойств функций.
v Применять производную для проведения приближенных вычислений, решать задачи прикладного характера на нахождение наибольшего и наименьшего значения.
v Вычислять в простейших случаях площади с использованием определенного интеграла;
v Решать прикладные задачи, в том числе, физические, на наибольшие и наименьшие значения функции на отрезке, на нахождение скорости и ускорения.
Знания:
v Значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы.
v Использовать математические законы, формулы, зависимости, графики и их интерпретацию в практической деятельности при решении технических, производственных и управленческих задач.
v Анализировать реальные числовые данные, представленные в виде диаграмм, графиков.
v Анализировать информацию статистического характера; основные понятия и методы математического анализа.
v Находить производные элементарных функций; производные сложных функций.
v Применять основные понятия, законы, теории в конкретных практических ситуациях: алгоритм исследования функции, признаки экстремума функции, признаки монотонности функции, нахождения наибольшего и наименьшего значения функции на отрезке.
v Использовать производную для исследования функций и построение графиков функций.
v Понятия неопределенного и определенного интеграла.
v Основные методы интегрирования. Формулы интегрирования. Формулу Ньютона-Лейбница. Основные математические методы решения прикладных задач в области профессиональной деятельности.
v Численное дифференцирование и интегрирование.
v Вычислять площадей фигур с использованием определенного интеграла.
3.Оценка освоения теоретического курса учебной дисциплины.
Основной целью оценки теоретического курса учебной дисциплины является оценка умений и знаний. Оценка теоретического курса учебной дисциплины осуществляется с использованием следующих форм и методов контроля: текущий контроль – тестирование/решение профессиональных задач; рубежный контроль – контрольная работа/самостоятельная работа; промежуточная аттестация – дифференцированный зачет. Дифференцированный зачет проводится в сроки, установленные учебным планом, и определяемые календарным учебным графиком образовательного процесса.
4.Задания для экзаменующегося.
Вариант 1.
Ознакомительный уровень.
Задание 1. Найти производную суммы: 8х2 + 4х.
|
а)16х + 4 |
б)8х+4 |
в) 0 |
г) 8х3 + 2х2. |
Задание 2. Вычислить предел
последовательности: ![]()
|
а)0 |
б) |
в) 2 |
г) нет решений |
Задание 3. Вычислить
предел функции: ![]() (х2 + 6)
(х2 + 6)
|
а)10 |
б)0 |
в) 8 |
г) |
Задание 4. Вычислить предел функции: ![]()
|
а)0 |
б) |
в) 4 |
г) нет решений |
Задание 5. Определить вид монотонности функции: у = 5х – 9.
|
а) убывает |
б) возрастает |
в) постоянная |
г) нет ответа |
Задание 6. Найти производную
функции: у = ln
![]()
|
а)
|
б)
ln
|
в)
|
г) |
Задание 7. Найти значение производной функции у = sin2x при x = 0.
|
а) 2
|
б) 0
|
в)1
|
г) |
Задание 8. Найти вторую производную: у = 9х2 -70.
|
а)9 |
б)18 |
в)0 |
г)нет ответа
|
Задание 9. Материальная точка движется по закону: S = 3t3+2t2-8 (м). Найти скорость движения точки через 2 секунды от начала движения.
|
а) 24
|
б) 2
|
в) 44 |
г) 32 |
Задание 10. Определить промежутки убывания функции: у = х3 – 3х.
|
а) (- |
б) R
|
в) (-1;1) |
г) [-1;1]
|
Репродуктивный уровень.
Задание 11. Найти
экстремумы функции: у = ![]()
Задание 12. Составить уравнение касательной: у = х2 + 2х, х0 = 1.
Задание 13. Вычислить неопределённый
интеграл: ![]() + 4х)dx
+ 4х)dx
Продуктивный уровень.
Задание 14. Найти скорость движения точки и ускорение через 2 секунды от начала движения, если формула для вычисления пути равна:
S= t4 + 3t3 - 3t (м/сек).
Задание 15. Выполнить подстановку в
неопределённом интеграле: ![]()
Ответы на тестовую (ознакомительную) часть промежуточной аттестации:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
а |
б |
а |
в |
б |
в |
а |
б |
в |
г |
Ответы на репродуктивную и продуктивную часть промежуточной аттестации:
|
11 |
12 |
13 |
14 |
15 |
|
нет экстремумов |
у = 4х – 1 |
х3 + 4х +С
|
65; 84 |
- |
Вариант 2.
Ознакомительный уровень.
Задание 1. Найти производную разности: 5х2 -10.
|
а)10х - 10 |
б)10х |
в) 0 |
г) нет решений |
Задание 2. Вычислить предел
последовательности: ![]()
|
а)0 |
б) |
в) 2 |
г)5 |
Задание 3. Найти значение производной у = cos3x при х = 0.
|
а)0 |
б) |
в) 2 |
г) нет решений
|
Задание 4.Найти вторую производную функции: у = 12х3
|
а) 36х2
|
б)72х
|
в) 0 |
г) 3х4
|
Задание 5. Материальная точка движется по закону: S = 2t3+3t2-5 (м). Найти скорость движения точки через 2 секунды от начала движения.
|
а) 36
|
б)72
|
в) 0 |
г) 31 |
Задание 6. Найти промежутки возрастания функции: у = - х3 + 3х.
|
а) (-
|
б) возрастает на D(y) |
в) (-1;1)
|
г) [-1;1]
|
Задание 7.Вычислить предел
последовательности: ![]()
|
а) 6
|
б)9
|
в) 0 |
г) не существует |
Задание 8. Вычислить неопределённый
интеграл: ![]()
|
а) 2х2 – 7х
|
б) 2х2 – 7х + С
|
в) 0 |
г) 31 |
Задание 9. Определить вид монотонности функции: у = 9х – 1.
|
а) убывает
|
б) возрастает
|
в) постоянная |
г) нет ответа |
Задание 10. Материальная точка движется по закону S = t3 + 4t – 6. Определить ускорение двитжения точки через 2 секунды.
|
а) 6
|
б)9
|
в) 12 |
г) 16 |
Репродуктивный уровень.
Задание 11. Найти
экстремумы функции: у = ![]()
Задание 12. Найти наибольшее и наименьшее значения: у = 4х2 - 4 на отрезке [-4;1].
Задание 13. Вычислить значение производной сложной функции:
у = ln![]() .
.
Продуктивный уровень.
Задание 14. Тело движется прямолинейно со скоростью V(t) = (2t3 + 1) м/с. Найдите путь, пройденный телом за промежуток времени от t=1с до t=3c.
Задание 15. Выполнить подстановку в
неопределённом интеграле: 
Ответы на тестовую (ознакомительную) часть промежуточной аттестации:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
б |
б |
а |
б |
а |
г |
б |
б |
а |
в |
Ответы на репродуктивную и продуктивную части промежуточной аттестации:
|
11 |
12 |
13 |
14 |
15 |
|
Нет экстремумов |
60 |
0,25 |
22 |
|
Вариант 3.
Ознакомительный уровень.
Задание 1. Найти производную суммы: у = 7х3 + 4
|
а) 21х |
б) 21х2 |
в) 21х2 + 4х |
г) нет ответа |
Задание 2. Вычислить предел
функции:![]()
|
а)0 |
б) |
в) 2 |
г)0,5 |
Задание 3. Найти значение производной у = 2 + 3х 3 при х = 0.
|
а)0 |
б) |
в) 2 |
г) нет решений
|
Задание 4.Найти вторую производную функции: у = 4х3 + 4
|
а) 12х2
|
б)24х
|
в) 0 |
г) 8х3
|
Задание 5. Материальная точка
движется по закону: S = sinx
(м). Найти ускорение движения точки через ![]() секунды от начала
движения.
секунды от начала
движения.
|
а) 36
|
б)1
|
в) 0 |
г) -1 |
Задание 6. Найти промежутки выпуклости вверх: у = - х3 + 3х.
|
а) (-
|
б) выпукла вниз на D(y) |
в)
(0;
|
г) [-1;1]
|
Задание 7.Вычислить предел
последовательности: ![]()
|
а) 6
|
б)9
|
в) |
г) не существует |
Задание 8. Вычислить неопределённый
интеграл: ![]()
|
а) 5х2 + 3х
|
б) 5 х2 +3х + С
|
в) 13 |
г) 10 |
Задание 9. Определить вид монотонности функции: у = -4х + 6
|
а) возрастает
|
б) убывает
|
в) постоянная |
г) нет ответа |
Задание 10. Материальная точка имеет скорость, которая выражается формулой V =3t2 + 2t . Определить путь, пройденный точкой за 2 секунды от начала движения.
|
а)16
|
б)9
|
в) 14 |
г) 12 |
Репродуктивный уровень.
Задание 11. Найти экстремумы функции: у = х2 + 9.
Задание 12. Найти наибольшее и наименьшее значения: у = х2 - 1 на отрезке [-2;1].
Задание 13. Вычислить определённый
интеграл: ![]() dx.
dx.
Продуктивный уровень.
Задание 14. Вычислить площадь фигуры, ограниченной функциями
у = -х2 и у = -х.
Задание 15. Выполнить подстановку в неопределённом интеграле:
![]()
Ответы на тестовую (ознакомительную) часть промежуточной аттестации:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
б |
в |
а |
б |
г |
в |
в |
б |
б |
г |
Ответы на репродуктивную и продуктивную части промежуточной аттестации:
|
11 |
12 |
13 |
14 |
15 |
|
(0;9) |
унаим( унаиб(-2) = 3 |
32 |
|
|
Вариант 4.
Ознакомительный уровень.
Задание 1. Найти производную суммы функций: х4 + х3 + 7
|
а)4х + 3х |
б)4х3 + 3х2 |
в) 4х3 + 3х |
г) 4х3 + 3х2 + 7 |
Задание 2. Вычислить предел
последовательности: ![]()
|
а)0 |
б) |
в) 2 |
г)15 |
Задание 3. Найти значение производной у = 2cosx при х = 0.
|
а)0 |
б) |
в) 2 |
г) нет решений
|
Задание 4.Найти вторую производную функции: у = 5х4
|
а) 60х2
|
б)72х
|
в) 0 |
г) 20х3
|
Задание 5. Материальная точка движется по закону: S = 2t3+3t2-5 (м). Найти ускорение движения точки через 2 секунды от начала движения.
|
а) 36
|
б)72
|
в) 0 |
г) 30 |
Задание 6. Найти промежутки выпуклости вниз: у = - х3 + 3х.
|
а) (-
|
б) выпукла вниз на D(y) |
в)
(0;
|
г) [-1;1]
|
Задание 7.Вычислить предел
последовательности: ![]()
|
а) 6
|
б)9
|
в) 3 |
г) не существует |
Задание 8. Вычислить неопределённый
интеграл: ![]()
|
а) 2,5х2 + 6х
|
б) 2,5 х2 +6х + С
|
в) 5 |
г) 31 |
Задание 9.![]() ( х2
+ 1).
( х2
+ 1).
|
а) 4
|
б)10
|
в) 7 |
г) 2 |
Задание 10. Материальная точка имеет скорость, которая выражается формулой V =4t3 + 4t . Определить путь, пройденный точкой за 2 секунды от начала движения.
|
а) 6
|
б)9
|
в) 24 |
г) 40 |
Репродуктивный уровень.
Задание 11. Найти экстремумы функции: у = х2 – 4.
Задание 12. Найти наибольшее и наименьшее значения: у = х2 + 4 на отрезке [-2;1].
Задание 13. Вычислить определённый
интеграл: ![]() dx
dx
Продуктивный уровень.
Задание 14. Вычислить площадь фигуры, ограниченной функциями
у = х2 и у = х.
Задание 15. Выполнить подстановку в неопределённом интеграле:
![]()
Ответы на тестовую (ознакомительную) часть промежуточной аттестации:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
б |
б |
а |
а |
г |
а |
в |
б |
б |
в |
Ответы на репродуктивную и продуктивную части промежуточной аттестации:
|
11 |
12 |
13 |
14 |
15 |
|
(0;-4) |
унаим(0) = 4 унаиб(-2) = 8 |
8 |
|
|
Вариант 5.
Ознакомительный уровень.
Задание 1. Определить вид монотонности функции: у = 5 – 7х.
|
а) убывает |
б) возрастает |
в) постоянная |
г) нет ответа |
Задание 2. Вычислить предел
последовательности: ![]()
|
а)0 |
б) |
в) 5 |
г)9 |
Задание 3. Найти значение производной у = 12x - х2 при х = 0.
|
а)0 |
б) |
в) 12 |
г) -2
|
Задание 4.Найти вторую производную функции: у = 5х4 + 8х
|
а) 60х2
|
б)72х
|
в) 0 |
г) 20х3 + 8
|
Задание 5. Найти угловой коэффициент касательной, проведённой к графику функции у = х2 + 5 в точке с абсциссой х0 = 1
|
а) 5
|
б)2
|
в) 6 |
г) 30 |
Задание 6. Найти промежутки выпуклости вниз: у = 6 х3 - 6х.
|
а) (-
|
б) выпукла вниз на D(y) |
в)
(0;
|
г) [-1;1]
|
Задание 7.Вычислить предел
последовательности: ![]()
|
а)
|
б)3
|
в) |
г) 7 |
Задание 8. Вычислить неопределённый
интеграл: ![]()
|
а) 2х2 + 2х3 + С
|
б) 2х2 + 2х3
|
в) -2 |
г) -2х3 |
Задание 9. Найти
предел функции: ![]() (5х3 – 9)
(5х3 – 9)
|
а) -9
|
б)9
|
в) 0 |
г) -4 |
Задание 10. Вычислить определённый
интнеграл:![]() dx
dx
|
а) 6
|
б)-3
|
в)- 4 |
г) 10 |
Репродуктивный уровень.
Задание 11. Найти экстремумы функции: у = х2 – 9.
Задание 12. Найти наибольшее и наименьшее значения: у = х2 - 1 на отрезке [-1;1].
Задание 13. Материальная точка имеет скорость, которая выражается формулой V =3t2 + 4t . Определить путь, пройденный точкой за 3 секунды от начала движения.
Продуктивный уровень.
Задание 14. Вычислить площадь фигуры, ограниченной функциями
у = х2 -2x и у = 0.
Задание 15. Найти значение
производной функции у = ![]() при x
= 0.
при x
= 0.
Ответы на тестовую (ознакомительную) часть промежуточной аттестации:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
а |
а |
в |
а |
б |
в |
в |
а |
а |
в |
Ответы на репродуктивную и продуктивную части промежуточной аттестации:
|
11 |
12 |
13 |
14 |
15 |
|
(0;9) |
унаим(0) = -1 унаиб( |
45 |
|
0 |
Вариант 6.
Ознакомительный уровень.
Задание 1. Найти ![]() (4х + 8)
(4х + 8)
|
а)12 |
б)8 |
в) 16 |
г)нет ответа |
Задание 2. Вычислить предел
последовательности: ![]()
|
а)0 |
б) |
в) 5 |
г)8 |
Задание 3. Найти значение производной у = 12x - cosх при х = 0.
|
а)0 |
б) |
в) 12 |
г) -2
|
Задание 4.Найти вторую производную функции: у = 5х4 + 8х -10,45
|
а) 60х2
|
б)72х
|
в) 0 |
г) 20х3 + 8
|
Задание 5. Найти угловой коэффициент касательной, проведённой к графику функции у = 2х2 -3 в точке с абсциссой х0 = 1
|
а) 5
|
б)2
|
в) 4 |
г) 30 |
Задание 6. Найти точку минимума функции: у = 6 х3 - 18х.
|
а) -1
|
б) -12 |
в) 1
|
г) [-1;1]
|
Задание 7.Вычислить предел
последовательности: ![]()
|
а) 38
|
б)19
|
в) |
г) 2 |
Задание 8. Вычислить неопределённый
интеграл: ![]()
|
а) х5 - 4х3 - 5х + С
|
б) х5 - 4х3 - 5х |
в) 20х3 – 24х |
г) 20х3 – 24х +С |
Задание 9. Определить
вид неопределённости: ![]()
|
а)
|
б)
|
в) |
г) нет ответа |
Задание 10. Вычислить определённый
интнеграл:![]() dx
dx
|
а) 6
|
б)2
|
в) 4 |
г) 10 |
Репродуктивный уровень.
Задание 11. Вычислить
предел последовательности: ![]()
Задание 12. Найти производную сложной функции: у = sin3 (х2 – 1).
Задание 13. Материальная точка имеет скорость, которая выражается формулой V =3t2 – 6t +5 . Определить путь, пройденный точкой от начала движения до остановки.
Продуктивный уровень.
Задание 14. Вычислить площадь фигуры, ограниченной функциями
у = -х2 +2x и у = 0.
Задание 15. Выполнить подстановку в неопределённом интеграле:
![]()
Ответы на тестовую (ознакомительную) часть промежуточной аттестации:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
в |
в |
в |
а |
в |
в |
б |
а |
а |
в |
Ответы на репродуктивную и продуктивную части промежуточной аттестации:
|
11 |
12 |
13 |
14 |
15 |
|
1 |
6х sin2(x2–1)cos(x2 – 1) |
3 |
|
|
Вариант 7.
Ознакомительный уровень.
Задание 1. Найти предел функции:![]() -8)
-8)
|
а)7 |
б)-7 |
в) -8 |
г) нет ответа |
Задание 2. Вычислить предел
последовательности: ![]()
|
а)1 |
б) |
в) 5 |
г)0 |
Задание 3. Найти значение
производной у = ![]() при х = 0.
при х = 0.
|
а)е |
б) |
в)
х |
г) -2
|
Задание 4.Найти вторую производную функции: у = sinx
|
а) sinx
|
б) -sinx
|
в) cosx |
г) 0 |
Задание 5. Найти тангенс угла наклона касательной, проведённой к графику функции у = х2 + 5 в точке с абсциссой х0 = 1
|
а) 5
|
б)2
|
в) 6 |
г) 30 |
Задание 6. Найти точку максимума функции: у = 6 х3 - 18х.
|
а) -1
|
б) -12 |
в) 1
|
г) [-1;1]
|
Задание 7.Вычислить предел
последовательности: ![]()
|
а) 9
|
б)3
|
в) 3 |
г) 6 |
Задание 8. Вычислить неопределённый
интеграл: ![]()
|
а) 7х2-20х3-5x+С
|
б) 7х2-20х3-5x |
в) 7х2-20х3-5x |
г) 7х2-20х3-5x+C |
Задание 9. Найти тангенс угла наклона касательной к функции у = х2 + 6 в точке с абсциссой х0 = 1.
|
а) нет ответа
|
б)0
|
в) 7 |
г) 2 |
Задание 10. Вычислить определённый
интнеграл:![]() dx
dx
|
а) -2
|
б)-3
|
в)- 4 |
г) 10 |
Репродуктивный уровень.
Задание 11. Вычислить
предел функции: ![]()
Задание 12. Найти наибольшее и наименьшее значения: у = х2 - 4 на отрезке [-2;2].
Задание 13. Материальная точка имеет скорость, которая выражается формулой V =3t2 + 4t . Определить путь, пройденный точкой за 3 секунды от начала движения.
Продуктивный уровень.
Задание 14. Вычислить площадь фигуры, ограниченной функциями
у = х3 , х = -1, у = 0
Задание 15. Выполнить подстановку в неопределённом интеграле:
![]()
Ответы на тестовую (ознакомительную) часть промежуточной аттестации:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
б |
а |
б |
б |
б |
а |
б |
а |
г |
в |
Ответы на репродуктивную и продуктивную части промежуточной аттестации:
|
11 |
12 |
13 |
14 |
15 |
|
|
унаим(0) = -4 унаиб( |
45 |
|
|
Вариант 8.
Ознакомительный уровень.
Задание 1. Найти угловой коэффициент касательной к графику функции
у = 2х2 – 8 в точке х0 = 2.
|
а)2 |
б) 8 |
в) 0 |
г)-8 |
Задание 2. Вычислить предел
функции:![]()
|
а)0 |
б) |
в) 2 |
г)0,5 |
Задание 3. Найти значение производной у = х 3 (x - 1) при х = 0.
|
а)0 |
б) |
в) 2 |
г) нет решений
|
Задание 4.Найти вторую производную функции: у = 2cosx
|
а)- 2cosx
|
б) 2cosx
|
в) -2sinx
|
г) 2sinx |
Задание 5. Материальная точка движется по закону: S = 3t2 + 8t (м).
Найти ускорение движения точки через 2 секунды от начала движения.
|
а) 6
|
б)6
|
в) 0 |
г) 28 |
Задание 6. Найти промежутки выпуклости вверх: у = - х3 + 3х.
|
а) (-
|
б) выпукла вниз на D(y) |
в)
(0;
|
г) [-1;1]
|
Задание 7.Вычислить предел
последовательности: ![]()
|
а) 6
|
б)9
|
в) |
г) не существует |
Задание 8. Вычислить неопределённый
интеграл: ![]()
|
а) 6х2 +x3 +5х+C
|
б) 6х2 +x3 +5х
|
в) 12+6x +C |
г) 12+6x |
Задание 9. Определить вид монотонности функции: у = х – 5.
а) убывает б) возрастает в)постоянная г)нет ответа
|
|
|
|
|
Задание 10. Материальная точка имеет скорость, которая выражается формулой V =3t2 + 2t . Определить путь, пройденный точкой за 2 секунды от начала движения.
|
а)16
|
б)9
|
в) 14 |
г) 12 |
Репродуктивный уровень.
Задание 11. Найти экстремумы функции: у = х2 + 9.
Задание 12. Найти наибольшее и наименьшее значения: у = х2 - 1 на отрезке [-2;1].
Задание 13. Вычислить определённый
интеграл: ![]() dx
dx
Продуктивный уровень.
Задание 14. Найти площадь фигуры, ограниченной функциями: у = х2 и у = х.
Задание 15. Выполнить подстановку в неопределённом интеграле:
![]()
Ответы на тестовую (ознакомительную) часть промежуточной аттестации:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
б |
в |
а |
а |
а |
в |
в |
а |
б |
г |
Ответы на репродуктивную и продуктивную части промежуточной аттестации:
|
11 |
12 |
13 |
14 |
15 |
|
(0;9) |
унаим( унаиб(-2) = 3 |
32 |
|
|
6. Перечень теоретических вопросов, выносимых на дифференцированный зачёт:
1.Определение предела последовательности.
2.Определение предела функции.
3.Способы нахождения пределов последовательности вида:
![]() .
.
4.Способы нахождения пределов последовательности вида:
![]() .
.
5.Способы нахождения пределов функции вида:![]() .
.
6.Написать формулу первого замечельного предела.
7.Написать формулу втого замечательного предела.
8.Сформулировать механический смысл первой производной.
9.Сформулировать геометричекий смысл производной.
10.Что называетсядифференцированием функции.
11.Написать уравнение касательной к графику функции в данной точке.
12.Производная постоянной величины равна…
13.При вычислении производной постоянный множитель можно…
14.Механический смысл второй производной.
15.Функция возрастает на заданном промежутке, если…
16. Функция убывает на заданном промежутке, если…
17. Назвать условия сущетвования минимума функции.
18. Назвать условия сущетвования максимума функции.
19. Назвать условия выпуклости графика функции.
20. Назвать условия вогнутости графика функции.
21. Определение первообразной для функции f на некотором промежутке.
22. Множество первообразных для данной функции f(х) называется…
23. Непосредственное интегрирование, метод подстановки, интегрирование по частям это…
24. Чему равна производная от неопределенного интеграла.
25. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен…
26.Сформулировать формулу Ньютона-Лейбница.
27. Чему равен определенный интеграл с одинаковыми пределами.
28. При перемене местами верхнего и нижнего пределов интегрирования определенный интеграл…
29. Определенный интеграл используется при вычислении…
а) площадей плоских фигур
б) объемов тел вращения
в) пройденного пути
г) всех перечисленных элементов
30.По какой формуле вычисляется путь, пройденный материальной точкой.
31.Написать формулу для вычисления площади криволинейной трапеции, если функции, образовывающая фигуру, положительна.
32. Написать формулу для вычисления площади криволинейной трапеции, если функции, образовывающая фигуру, отрицательна.
33. Написать формулу для вычисления площади криволинейной трапеции, если фигуру образуют две функции.
Перечень практичеких задач, выносимых на диффренцированный зачёт:
Тема: Пределы.
Ознакомительный уровень.
1.Вычислить предел последовательности: ![]()
2.Вычислить предел функции: ![]()
3.Вычислить предел последовательности: ![]()
4.Вычислить предел последовательности: ![]()
5. Вычислить предел
функции:![]()
6. Вычислить предел последовательности: ![]() .
.
7. Вычислить предел последовательности: ![]() .
.
8. Вычислить предел последовательности: ![]()
9. Вычислить предел функции: ![]()
10. Вычислить предел последовательности: ![]()
11. Вычислить предел: ![]() .
.
12. Вычислить предел последовательности: ![]()
13. Вычислить предел функции:![]() .
.
14. Вычислить предел последовательности: ![]() .
.
Репродуктивный уровень.
1.Вычислить предел последовательности: ![]()
2.Вычислить предел последовательности: ![]() .
.
Продуктивный уровень.
1. Вычислить предел функции: ![]() .
.
2.Вычислить предел: ![]() –
– ![]() ).
).
Тема: Производная. Приложение производной к исследованию функции.
Ознакомительный уровень.
1. . Найти значение
производной у = ![]() при х = 0.
при х = 0.
2. Найти значение производной функции у = sin2x при x = 0.
3. Найти вторую производную функции у =
8![]()
4. Материальная точка движется по закону: S = 3t3+2t2-8 (м). Найти скорость движения точки через 2 секунды от начала движения.
5. Определить промежутки убывания функции: у = х3 – 3х.
6. Найти значение производной у = cos3x при х = 0.
7. Найти вторую производную функции: у = 12х3
8. Материальная точка движется по закону: S = 2t3+3t2-5 (м). Найти скорость движения точки через 2 секунды от начала движения.
9.Найти промежутки возрастания функции: у = - х3 + 3х.
10. Материальная точка движется по закону S = t3 + 4t – 6. Определить ускорение двитжения точки через 2 секунды.
11. Найти значение производной у = 2 + 3х 3 при х = 0.
12. Найти вторую производную функции: у = 4х3 + 4.
13. Материальная точка движется по закону: S
= sinx (м). Найти ускорение движения точки
через ![]() секунды от начала
движения.
секунды от начала
движения.
14. Найти промежутки выпуклости вверх: у = - х3 + 3х.
15. Найти экстремумы функции: у = х2 + 9.
16. Найти значение производной у = 2cosx при х = 0.
17. Найти вторую производную функции: у = 5х4.
18. Материальная точка движется по закону: S = 2t3+3t2-5 (м). Найти ускорение движения точки через 2 секунды от начала движения.
19.Найти промежутки выпуклости вниз: у = - х3 + 3х.
20. Найти значение производной у = 12x - х2 при х = 0.
21. Найти вторую производную функции: у = 5х4 + 8х.
22. Найти угловой коэффициент касательной, проведённой к графику функции у = х2 + 5 в точке с абсциссой х0 = 1.
23.Найти значение производной у = 12x - cosх при х = 0.
24. Найти вторую производную функции: у = 5х4 + 8х -10,45.
25. Найти угловой коэффициент касательной, проведённой к графику функции у = 2х2 -3 в точке с абсциссой х0 = 1.
26. Найти точку минимума функции: у = 6 х3 - 18х.
27. Найти вторую производную функции: у = 2cosx.
Репродуктивный уровень.
1.Найти экстремумы функции: у = ![]()
2.Составить уравнение касательной: у = х2 + 2х, х0 = 1.
3. Найти экстремумы функции: у = ![]()
4. Найти наибольшее и наименьшее значения: у = 4х2 - 4 на отрезке [-4;1].
5. Найти наибольшее и наименьшее значения: у = х2 - 1 на отрезке [-2;1].
6. Найти экстремумы функции: у = х2 – 4.
7. . Найти наибольшее и наименьшее значения: у = х2 + 4 на отрезке
[-2;1].
8. Найти промежутки выпуклости вниз: у = 6 х3 - 6х.
9. Найти экстремумы функции: у = х2 – 9.
10. Найти наибольшее и наименьшее значения: у = х2 - 1 на отрезке [-1;1].
11. Найти производную функции: у = ln
![]() .
.
12. Найти тангенс угла наклона касательной, проведённой к графику функции у = х2 + 5 в точке с абсциссой х0 = 1.
13. Найти наибольшее и наименьшее значения: у = х2 - 4 на отрезке [-2;2].
14. Найти значение производной у = х 3 (x - 1) при х = 0.
15. Материальная точка движется по закону: S = 3t2 + 8t (м).
Найти ускорение движения точки через 2 секунды от начала движения.
16. Найти промежутки выпуклости вверх: у = - х3 + 3х.
17. Найти экстремумы функции: у = х2 + 16.
18. Найти наибольшее и наименьшее значения: у = х2 - 1 на отрезке [-2;1].
Продуктивный уровень.
1. Найти производную сложной функции: у = sin3 (х2 – 1).
2. Построить график функции: у = х3 – 3х.
3. Построить график функции: у = - х3 + 3х.
Тема: Неопределённый интеграл. Определённый интеграл.
Ознакомительный уровень.
1.Вычислить неопределённый интеграл: ![]() .
.
2. Вычислить неопределённый интеграл: ![]() .
.
3. Вычислить неопределённый интеграл: ![]() .
.
4. . Вычислить неопределённый интеграл: ![]() .
.
5. Вычислить неопределённый интеграл: ![]() .
.
6. Вычислить неопределённый интеграл: ![]() .
.
7. Вычислить неопределённый интеграл: ![]() .
.
Репродуктивный уровень.
1.Вычислить неопределённый интеграл: ![]() + 4х)dx
+ 4х)dx
2. Вычислить определённый интеграл: ![]() dx
dx
3. Вычислить определённый интеграл: ![]() dx.
dx.
4. Вычислить определённый интеграл: ![]() dx.
dx.
5. Вычислить определённый интнеграл:![]() dx.
dx.
6. Материальная точка имеет скорость, которая выражается формулой
V =3t2 + 4t. Определить путь, пройденный точкой за 3 секунды от начала движения.
7.Вычислить определённый интнеграл:![]() dx.
dx.
8. Материальная точка имеет скорость, которая выражается формулой
V =3t2 – 6t +5 . Определить путь, пройденный точкой от начала движения до остановки.
9. Вычислить определённый интнеграл:![]() dx.
dx.
10. Материальная точка имеет скорость, которая выражается формулой V =3t2 + 2t . Определить путь, пройденный точкой за 2 секунды от начала движения.
11. Вычислить определённый интеграл: ![]() dx.
dx.
Продуктивный уровень.
1.Найти скорость движения точки и ускорение через 2 секунды от начала движения, если формула для вычисления пути равна: S= t4 + 3t3 - 3t (м/сек).
2.Выполнить подстановку в неопределённом интеграле: ![]() .
.
3.Тело движется прямолинейно со скоростью V(t) = (2t3 + 1) м/с. Вычислить путь, пройденный телом за промежуток времени от t = 1с до t = 3c.
4.Выполнить подстановку в неопределённом интеграле:  .
.
5.Материальная точка имеет скорость, которая выражается формулой V =3t2 + 2t . Определить путь, пройденный точкой за 2 секунды от начала движения.
6.Вычислить площадь фигуры, ограниченной функциями у = -х2 и у = -х.
7.Выполнить подстановку в неопределённом интеграле: ![]() .
.
8.Материальная точка имеет скорость, которая выражается формулой
V =4t3 + 4t. Определить путь, пройденный точкой за 2 секунды от начала движения.
9.Вычислить площадь фигуры, ограниченной функциями у = х2 и у = х.
10.Выполнить подстановку в неопределённом интеграле: ![]()
11.Вычислить площадь фигуры, ограниченной функциями у = х2 -2x и
у = 0.
12.Выполнить подстановку в неопределённом интеграле: ![]()
13.Вычислить площадь фигуры, ограниченной функциями у = -х2 +2x и
у = 0.
14.Выполнить подстановку в неопределённом интеграле: ![]()
15.Вычислить площадь фигуры, ограниченной функциями у = х3 , х = -1,
у = 0.
16.Выполнить подстановку в неопределённом интеграле: ![]() .
.
17.Вычислить площадь фигуры, ограниченной функциями у = -х2 и у = -х.
18.Выполнить подстановку в неопределённом интеграле: ![]() .
.
|
|
|
|
|
7.Критерии оценки:
Дифференцированный зачёт / Промежуточная аттестация.
«20» баллов выставляется за выполнение 100 % заданий, выданных преподавателем; умение работать со всеми видами источников, проявив самостоятельность и знания межпредметного характера; применение учебной дисциплины в жизни.
«15» баллов выставляется за выполнение не менее 80 % заданий, выданных преподавателем, без существенных ошибок: в его ответе содержатся недочеты или одна негрубая ошибка; при ответе на поставленные вопросы имеются незначительные замечания и поправки со стороны преподавателя. Обучающийся умеет самостоятельно добывать знания, пользуясь различны-ми источниками, имеет развитые практические умения.
«10» баллов выставляется студенту за выполнение 60% заданий или выполнение всех заданий с несколькими существенными ошибками; при ответе на поставленные вопросы преподаватель оказывал ему значительную помощь в виде наводящих вопросов. Обучающийся знает только основные принципы, умеет получать знания лишь из основных источников, имеет частично сформированные знания и умения.
«5» баллов выставляется студенту за выплнение 50% заданий, его ответы содержат более двух грубых ошибок; при ответе на поставленные вопросы преподаватель оказывал ему постоянную помощь. Обучающийся не умеет самостоятельно работать с источниками, не знает принципов учебной дисциплины, у него не сформированы знания и умения.
.
«0» баллов выставляется студенту за выполнение менее чем 50% заданий, его ответ содержит более двух грубых ошибок; при ответе на поставленные вопросы преподаватель оказывал ему постоянную помощь. Обучающийся не умеет самостоятельно работать с источниками, не знает принципов учебной дисциплины, у него не сформированы знания и умения.
Для сдачи зачёта, студенту необходимо набрать не менее 10 баллов.
8.Литература для подготовки к зачёту (на зачёте использовать нельзя):
Учебники и учебные пособия:
1. Э.С. Маркович «Курс высшей математики», Э.С. Маркович М., 2007 г
2. Н.В. Богомолов «Математика» СПОМ, Н.В. Богомолов «Дрофа», 2008г
3. М.Демидович «Задачи и упражнения по математическому анализу» М.Демидович, М., АСТ, 2006г.
4. О.Н. Афанасьева «Дидактические материалы для ссузов» под редакцией О.Н. Афанасьевой, М., «Высшая школа», 2009г.
5. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. Кремер Н.Ш. – 2-е издание, переработанное и дополненное – М.: ЮНИТИ-ДАНА, 2004. – 573с.
6. Спирина М.С. Теория вероятностей и математическая статистика: учебник для студентов учреждений среднего профессионального образования / М.С. Спирина, П.А. Спирин. – М.: Издательский центр «Академия», 2007. – 352с.
7.Григорьев С.Г. Математика: учебник для студентов средних профессинальных учреждений / С.Г. Григорьев, С.В. Задулина; под ред. В.А. Гусева. – 2-е изд., стер. – М.: Издательский центр «Академия», 2007. – 384 с.:
Методические пособия:
1. Справочный материал и методические указания для самостоятельной ра-боты по математике студентов - заочников. – Калининград, ГАУ СПО КСТ, 2011.
2. Яковлев Г.Н. Алгебра и начала анализа (Математика для техникумов) [Электронный учебник] /Г.Н Яковлев. - Режим доступа: http://lib.mexmat.ru/books/78472/.
3. Калашникова В.А. Методическое пособие: «Конспекты лекций по математике» [Электронный ресурс] /В.А. Калашникова. - Режим доступа: http://www.exponenta.ru/educat/systemat/kalashnikova/inde/.
4. Курош А.Г. Курс высшей алгебры [Электронный учебник] /А.Г. Курош. - Режим доступа: http://www.gaudeamus.omskcity.com/PDF_library_natural-science_8.html/
5. Кострикин А.И. Линейная алгебра и геометрия [Электронный учебник] /А.И. Кострикин, Манин Ю.И. - Режим доступа: http://www.gaudeamus.omskcity.com/PDF_library_natural-science_8.html/
Справочная литература:
1) Выгодский М.Я. Справочник по высшей математике. Выгодский М.Я. -М.: Наука, 2007.
2) Ляшко И.И Справочное пособие по высшей математике. Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П. Т.1: Математический анализ: введение в анализ, производная, интеграл. – М.: Едиториал УРСС, 2008. – 360 с.
Интернет-ресурсы:
1.http://www.youtube.com/watch?v=1546Q24djU4&feature=channel
(Лекция 8. Основные сведения о рациональных функциях)
2. http://www.youtube.com/watch?v=TxFmRLiSpKo
(Геометрический смысл производной)
3.http://www.youtube.com/watch?v=PbbyP8oEv-g
(Лекция 1. Первообразная и неопределенный интеграл)
http://www.youtube.com/watch?v=2N-1jQ_T798&feature=channel
(Интегрирование по частям)
5.http://www.youtube.com/watch?v=3qGZQW36M8k&feature=channel
(Лекция 2. Таблица основных интегралов)
6. http://www.youtube.com/watch?v=7lezxG4ATcA&feature=channel
(Лекция 3. Непосредственное интегрирование)
7.http://www.youtube.com/watch?v=s-FDv3K1KHU&feature=channel
(Лекция 4. Метод подстановки)
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Калязинский колледж им. Н.М. Полежаева
УЧЕБНО-ПРАКТИЧЕСКОЕ ПОСОБИЕ
«СБОРНИК ПРАКТИЧЕСКИХ РАБОТ»
190604 Техническое обслуживание и ремонт автомобильного транспорта
151001 Технология машиностроения
080114 «Экономика и бухгалтерский учет (по отраслям)»
Калязин
2013 год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Сборник практических работ рекомендован для преподавателей математики и студентов 2 курса, обучающихся по специальностям 190604, 151001 и 080114.
Сборник практических работ является частью методического обеспечения учебного процесса. Материалы составлены в соответствии с федеральными государственными образовательными стандартами СПО для специальностей 190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)». Сборник практических работ направлен на приобретение практических навыков при решении прикладных задач; содержит семь практических работ и одну контрольную работу (рубежный контроль), ответы к ним. Материалы могут быть использованы при дистанционной форме обучения студентов.
Сборник практических работ: МАТЕМАТИКА, 2 курс (190604,151001,080114) / Старикова Наталия Валерьевна.
Калязин: ГБОУ СПО Калязинский колледж им. Н.М.Полежаева , 2013, – 32с.
Раздел 1. «Основы дифференциального исчисления».
Студент должен:
Знать:
· определение числовой функции, способы ее задания
· простейшие преобразования графиков функций;
· определение предела последовательности;
· формула второго замечательного предела;
· определение предела функции в точке;
· свойства предела функции в точке;
· формула первого замечательного предела
уметь:
находить пределы последовательности вида:![]() ;
;
·
находить
пределы последовательности вида: ![]() ;
;
·
находить
пределы вижда: ![]() .
.
· вычислять пределы функии в точке
·
предел
функции вида: ![]() .
.
· вычислять пределы функций на бесконечности;
· вычислять примеры на превый замечательный предел.
Практическая работа №1. «Пределы»
|
Вариант 1 Вычислить пределы: Ознакомительный уровень. 1)
2)
3)
4)
Репродуктивный уровень: 5)
6)
Продуктивный уровень: 7)
8)
|
Вариант 2 Вычислить пределы: Ознакомительный уровень. 1)
2)
3) 4) Репродуктивный уровень: 5)
6) Продуктивный уровень: 7) 8)
|
|
Вариант 3. Вычислить пределы: Ознакомительный уровень: 1)
2) 3) 4)
Репродуктивный уровень: 5) 6) Продуктивный уровень: 7) 8)
|
Вариант 4. Вычислить пределы: Ознакомительный уровень: 1)
2) 3) 4)
Репродуктивный уровень: 5) 6) Продуктивный уровень: 7) 8)
|
|
Вариант 5. Вычислить пределы: Ознакомительный уровень: 1)
2) 3) 4) Репродуктивный уровень: 5) 6) Продуктивный уровень: 7) 8)
|
Вариант 6. Вычислить пределы: Ознакомительный уровень: 1) 2) 3) 4) Репродуктивный уровень: 5) 6) Продуктивный уровень: 7) 8)
|
Ответы:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
В1 |
|
-0,6 |
0 |
4 |
5 |
8 |
2 |
|
|
В2 |
0,25 |
|
0 |
11 |
|
10 |
-1 |
0 |
|
В3 |
|
0 |
|
4 |
5 |
14 |
|
|
|
В4 |
|
|
0 |
6 |
6 |
20 |
|
0 |
|
В5 |
-0,5 |
0 |
|
51 |
5 |
2 |
0,25 |
0,5 |
|
В6 |
5 |
0 |
|
12 |
0,5 |
12 |
-1 |
4,5 |
Критерии оценки: Практическая работа №1. «Пределы».
«4» балла за выполнение 100 % заданий, выданных преподавателем, без существенных ошибок.
«3» балла за 70 % выполнения задания с насколькими несущественными ошибками.
«2» балла за 50% заданий или выполнение всех заданий с несколькими существенными ошибками.
«1» балл за выполнение всех заданий с существенными ошибками.
«0» баллов - невыполнение заданий.
Для того чтобы задание было зачтено, студенту необходимо набрать не менее 2 баллов.
Раздел 2. «Основы дифференциального исчисления».
Раздел 3. «Приложение производной к исследованию функций»
Студент должен:
знать:
· определение производной, ее геометрический и механический смысл;
правила и формулы дифференцирования функций;
· определение дифференциала функции и его геометрический смысл; определение второй производной, ее физический смысл;
· необходимые и достаточные условия возрастания и убывания функции, существования экстремума;
· необходимые и достаточные условия выпуклости и вогнутости графика функции;
· определение точки перегиба;
· общую схему построения графиков функций с помощью производной;
· правило нахождения наибольшего и наименьшего значения функции на промежутке;
уметь:
· дифференцировать функции, используя таблицу производных и правила;
· дифференцирования, находить производные сложных функций;
· вычислять значение производной функции в указанной точке;
· находить угловой коэффициент и угол наклона касательной, составлятьуравнение касательной и нормали к графику функции в данной точке;
· находить скорость изменения функции в точке;
· применять производную для исследования реальных физических процессов;
· находить производные второго порядка, применять вторую производную для решения физических задач
· находить дифференциал функции, с помощью дифференциала приближенно;
· вычислять значение и приращение функции в указанной точке;
· применять производную для нахождения промежутков монотонности и экстремумов функции;
· находить с помощью производной промежутки выпуклости и вогнутости;
· графика функции, точки перегиба;
· проводить исследования и строить графики многочленов;
· находить наибольшее и наименьшее значения функции, непрерывной на промежутке;
· решать несложные прикладные задачи на нахождение наибольших и наименьших значений реальных величин.
Практическая работа №2 «Вычисление производных»
|
Вариант 1. Найти производные следующих функций: Ознакомительный уровень. 1.у = 0,2х2 + 5 х – 47 2. у = х – 5- х 3.у = (х-2)(х2+8) 4.у
= Репродуктивный уровень. 5.у = (х2 + 3х)3 6.у
= ln
7.у
= Продуктивный уровень. 8.у = sin cos 5x 9.у
=
|
Вариант 2. Найти производные следующих функций: Ознакомительный уровень. 1.у = 0,5х2 - 6 х – 4 2. у = х – 3+ х 3.у = (х-5)(х2+5) 4.у
= Репродуктивный уровень. 5.у = (х3 + 6х)4 6.у
= ln
7.у
= Продуктивный уровень. 8.у = sin2 5x 9.у
=
|
|
Вариант 3. Найти производные следующих функций: Ознакомительный уровень. 1.у = 2х4 + 5 х2 – 4 2. у = х – 6- 5х 3.у = (5х-12)(2х2-2) 4.у
= Репродуктивный уровень. 5.у = (х5 + 4х)5 6.у
= ln
7.у
= Продуктивный уровень. 8.у = ln cos 5x 9.у
=
|
Вариант 4. Найти производные следующих функций: Ознакомительный уровень. 1.у = 5х4 + 7 х – 7 2. у = х – 7- 8х 3.у = (3х-5)(3х2-2) 4.у
= Репродуктивный уровень. 5.у = (2х6 + 9х)4 6.у
= ln
7.у
= Продуктивный уровень. 8.у = ln sin 5x 9.у
=
|
|
Вариант 5. Найти производные следующих функций: Ознакомительный уровень. 1.у = 7х2 + 3 х – 24 2. у = х – 7- 7х 3.у = (4х-1)(3х2+8) 4.у
= Репродуктивный уровень. 5.у = (х5 + х)8 6.у
= ln
7.у
= Продуктивный уровень. 8.у = sin ln 5x 9.у
=
|
Вариант 6. Найти производные следующих функций: Ознакомительный уровень. 1.у = 10х2 + 2х – 15 2. у = х – 5- х 3.у = (6х-3)(2х2+1) 4.у
= Репродуктивный уровень. 5.у = (х9 + 5х)4 6.у
= ln
7.у
= Продуктивный уровень. 8.у = cos cos 5x 9.у
=
|
Ответы:
|
Вариант 1. |
Вариант 2. |
Вариант 3. |
|
1.0,4х+5 2.-5х-6+1 3.3х2+4 4.
|
1.х-6 2.-3х-4+1 3.3х2+5-10x 4. |
1.10х+8х3 2.-6х-7-5 3.30х2- 48х - 10 4. |
|
5.3(х2+3х)2(2х+3) 6. 7.4х3 |
5.4(х3+6х)3(3х2+6) 6. 7.14х6 |
5.5(х5+4х)4(5х4+4) 6. 7.7х6 |
|
8.-5sin5xcoscos5x 9.
|
8.sin10x 9. |
8.-5tg5x 9. |
|
Вариант 4. |
Вариант 5. |
Вариант 6. |
|
1.20х3+7 2.-7х-8- 8 3.27х2 - 30x - 6 4.
|
1.14х+3 2.-7х-8-7 3.36х2+32 – 6x 4. |
1.20х+2 2.-5х-6-1 3.36х2+6 – 12x 4. |
|
5.4(2х6+9х)3(12х+9) 6. 7.8х7
|
5.8(х5+х)7(5х4+1) 6. 7.10х9 |
5.4(х9+5х)3(9х8+5) 6. 7.1 |
|
8.5ctg5x 9. |
8. 9. |
8.5sincos5xsin5x 9. |
Критерии оценки:
Практическая работа №2. «Вычисление производных».
«4» балла за выполнение 100 % заданий, выданных преподавателем, без существенных ошибок.
«3» балла за 70 % выполнения задания с несколькими несущественными ошибками.
«2» балла за 50% заданий или выполнение всех заданий с несколькими существенными ошибками.
«1» балл за выполнение всех заданий с существенными ошибками.
«0» баллов - невыполнение заданий.
Для того чтобы практическая работа была зачтена, студенту необходимо набрать не менее 2 баллов.
Практическая работа №3.
«Геометрический смысл функции.
Физический смысл производной».
|
Вариант 1. Ознакомительный уровень. 1.Составить уравнение касательной: у =х2 + 2х, х0 = 1. 2. Составить уравнение нормали: у = х2 - 2х, х0 = 0. Репродуктивный уровень. 3.Найти скорость движения точки и ускорение через 2 секунды от начала движения, если формула для вычисления пути равна: S= 2t3 + 2t2 - 3t +4 м. Продуктивный уровень. 4.Найти точки графика функции у
= еx
+
е-x,
в которых касательная к этому графику параллельна прямой |
Вариант 2. Ознакомительный уровень. 1.Составить уравнение касательной: у =х2 - 4х, х0 = 2. 2. Составить уравнение нормали: у = х2 – 6х, х0 = 0. Репродуктивный уровень. 3.Найти скорость движения точки и ускорение через 2 секунды от начала движения, если формула для вычисления пути равна: S= 3t3 + 5t2 – t +8 м. Продуктивный уровень. 4.Какой
угол: острый или тупой образует с положительным направлением оси х
касательная к графику функции у = х + |
||
|
Вариант 3. Ознакомительный уровень. 1.Составить уравнение касательной: у =х2 + 6х, х0 = 1. Составить уравнение нормали: у = х2 – 3, х0 = 1. Репродуктивный уровень. 3.Найти скорость движения точки и ускорение через 3 секунды от начала движения, если формула для вычисления пути равна: S= 3t3 + 4t2 – 2t +6 м/сек. Продуктивный уровень. 4.Найти точки графика функции у = е 2x-1 + 2х, в которых касательная к этому графику параллельна прямой у = 4х + 1. |
Вариант 4. Ознакомительный уровень. 1.Составить уравнение касательной: у =х2 + 8х, х0 = 1. Составить уравнение нормали: у = х2 – 6, х0 = 1. Репродуктивный уровень. 3.Найти скорость движения точки и ускорение через 4 секунды от начала движения, если формула для вычисления пути равна: S= t3 + t2 – 3t +10 м/сек. Продуктивный уровень. 4.Найти точки графика функции у=х2 – ln(2x-1), в которых касательная к этому графику параллельна прямой y = 2x – 3.
|
||
|
Вариант 5. Ознакомительный уровень. 1.Составить уравнение касательной: у =х2 – 6х, х0 = 2. Составить уравнение нормали: у = х2 – 10, х0 = 1. Репродуктивный уровень. 3.Найти скорость движения точки и ускорение через 4 секунды от начала движения, если формула для вычисления пути равна: S= t3 + 5t2 – 2t +3 м/сек. Продуктивный уровень. 4.В какой точке касательная к кривой у = lnx наклонена к оси ОХ по углом 450.
Ответы: |
Вариант 6. Ознакомительный уровень. 1.Составить уравнение касательной: у =х2 -8х, х0 = 2. Составить уравнение нормали: у = х2 – 7, х0 = 1. Репродуктивный уровень. 3.Найти скорость движения точки и ускорение через 3 секунды от начала движения, если формула для вычисления пути равна: S= 8t3 + t2 – 5t +2 м/сек. Продуктивный уровень. 4.Какой угол: острый или тупой образует с положительным направлением оси Х касатнельная к графику функции у=(1-2х)3 в точке с абсциссой х0 = 2.
|
||
|
Вариант 1. |
Вариант 2. |
Вариант 3. |
|
|
1.у = 4х – 1 2.у = 0,5х |
1.у = -4 2.у
= |
1.у=8х-1 2.у=-0,5х-1,5 |
|
|
3.29;28 |
3.55;46 |
3.103; 62 |
|
|
4.(ln2; 2,5) |
4.tg |
4.(0,5;2) |
|
|
Вариант 4. |
Вариант 5. |
Вариант 6. |
|
|
1.у=10х-1 2.у=-0,5х-4,5 |
1.у=-2х 2.у=-0,5х-8,5 |
1.у=0,25х-12,5 2.у=-0,5х-5,5 |
|
|
3.53; 26 |
3.86; 34 |
3.217; 146 |
|
|
4.(1,5; 2,25-ln2) |
4. (1;0) |
4.
tg |
|
Критерии оценки:
Практическая работа №3.
«Геометрический смысл изменения функции.
Физический смысл производной».
«4» балла за выполнение 100 % заданий, выданных преподавателем, без существенных ошибок.
«3» балла за 70 % выполнения задания с несколькими несущественными ошибками.
«2» балла за 50% заданий или выполнение всех заданий с несколькими существенными ошибками.
«1» балл за выполнение всех заданий с существенными ошибками.
«0» баллов - невыполнение заданий. Для того чтобы практическая работа была зачтена, студенту необходимо набрать не менее 2 баллов.
Практическая работа №4.
«Нахождение промежутков монотонности функции.
Нахождение экстремумов функции».
|
Вариант 1. Ознакомительный уровень. 1.Исследовать функцию на монотонность: у = х2+2х-4 2. Найти точки экстремумов функции: у = х2-2х+9 Репродуктивный уровень. 3.Исследовать функцию на монотонность и экстремумы. у
= Продуктивный уровень. 4. Найти промежутки возрастания и убывания функции:
5. Определить экстремумы функции с помощью 1 производной
|
Вариант 2. Ознакомительный уровень. 1.Исследовать функцию на монотонность: у = х2+4х-6 2. Найти точки экстремумов функции: у = х2-4х+10 Репродуктивный уровень. 3.Исследовать функцию на монотонность и экстремумы. у
= Продуктивный уровень. 4. Найти промежутки возрастания и убывания функции: у
= ln 5. Определить экстремумы функции с помощью 1 производной у=(х2-8)ех
|
|
Вариант 3. Ознакомительный уровень. 1.Исследовать функцию на монотонность: у =- х2+2х. 2. Найти точки экстремумов функции: у = х2-6х+1 Репродуктивный уровень. 3.Исследовать функцию на монотонность и экстремумы. у
= Продуктивный уровень. 4.
Найти промежутки возрастания и убывания функции: у
= 5.
Определить экстремумы функции с помощью 1 производной: у=
|
Вариант 4. Ознакомительный уровень. 1.Исследовать функцию на монотонность: у = х2+8х-23. 2. Найти точки экстремумов функции: у = х2-2х+9 Репродуктивный уровень. 3.Исследовать функцию на монотонность и экстремумы. у
= Продуктивный уровень. 4. Найти промежутки возрастания и убывания функции: у = х3lnx. 5.
Определить экстремумы функции с помощью 1 производной: у
=
|
|
Вариант 5. Ознакомительный уровень. 1.Исследовать функцию на монотонность: у = х2-4х+5. 2.Найти точки экстремумов функции: у = 2х2-4х+19 . Репродуктивный уровень. 3.Исследовать функцию на монотонность и экстремумы. у = Продуктивный уровень. 4. Найти промежутки возрастания и убывания функции: y=lnx2. 5.
Определить экстремумы функции с помощью 1 производной: y
=
|
Вариант 6. Ознакомительный уровень. 1.Исследовать функцию на монотонность: у = -х2+12х . 2.Найти точки экстремумов функции: у = 3х2-6х+15. Репродуктивный уровень. 3.Исследовать функцию на монотонность и экстремумы. у = Продуктивный уровень. 4. Найти промежутки возрастания и убывания функции: y=lnx3. 5.
Определить экстремумы функции с помощью 1 производной: у =
|
Ответы:
|
Вариант 1. |
Вариант 2. |
Вариант 3. |
|
1.у
у 2.хmin=1 |
1.
у
у 2.хmin=2 |
1.
у
у 2.хmin=3 |
|
3.убывает на D(y) Экстремумов нет |
3.убывает на D(y) Экстремумов нет |
3.убывает на D(y) Экстремумов нет |
|
4.
у
у 5.уmin(0)=0
уmax(2)= |
4.убывает на D(y) 5.уmin(2)=-4е2
уmax(2)= |
4.возрастает на D(y) 5. экстремумов нет |
|
Вариант 4. |
Вариант 5. |
Вариант 6. |
|
1.у
у 2.хmin=1 |
1.у
у 2.хmin=1 |
1.у
у 2.хmin=1 |
|
3. возрастает на D(y) Экстремумов нет. |
3.убывает на D(y) Экстремумов нет. |
3.возрастает на D(y) Экстремумов нет. |
|
4.
у
у 5.экстремумов нет |
4. возрастает на D(y) 5. уmin(1) = е
|
4. возрастает на D(y) 5.уmin(-1) = -1,5 уmax(1) = 1,5 |
Критерии оценки:
Практическая работа №4.
«Нахождение промежутков монотонности функции.
Нахождение экстремумов функции».
«4» балла за выполнение 100 % заданий, выданных преподавателем, без существенных ошибок.
«3» балла за 70 % выполнения задания с несколькими несущественными ошибками.
«2» балла за 50% заданий или выполнение всех заданий с несколькими существенными ошибками.
«1» балл за выполнение всех заданий с существенными ошибками.
«0» баллов - невыполнение заданий.
Для того чтобы практическая работа была зачтена, студенту необходимо
набрать не менее 2 баллов.
Практическая работа №5.
«Вторая производная. Приложение второй производной к исследованию функции».
|
Вариант 1. Ознакомительный уровень. 1.Исследовать функцию на выпуклость и точки перегиба: у = х3 + 3х. 2.Исследовать функцию на выпуклость и точки перегиба: у = х2+8. Репродуктивный уровень. 3.Исследовать функцию на выпуклость и найти точки перегиба у = х ех. Продуктивный уровень. 4.Построить
график ускорения точки, движение которой задано уравнением: S(t)
=
|
Вариант 2. Ознакомительный уровень. 1.Исследовать функцию на выпуклость и точки перегиба: у = -х3 + 3х. 2.Исследовать функцию на выпуклость и точки перегиба: у = 2х2 – 5х +2. Репродуктивный уровень. 3.Исследовать функцию на выпуклость и найти точки перегиба у = х е-х. Продуктивный уровень. 4.Построить
график ускорения точки, движение которой задано уравнением: S(t)
=
|
||
|
Вариант 3. Ознакомительный уровень. 1.Исследовать функцию на выпуклость и точки перегиба у = 3х3 + х. 2. Исследовать функцию на выпуклость и точки перегиба у = 6х2 – 3х +4. Репродуктивный уровень. 3. Исследовать функцию на выпуклость и найти точки перегиба у = хlnx. Продуктивный уровень. 4.
Построить график ускорения точки, движение которой задано уравнением: S(t)
=
|
Вариант 4. Ознакомительный уровень. 1.Исследовать функцию на выпуклость и точки перегиба у = -2х3 + 5х. 2. Исследовать функцию на выпуклость и точки перегиба у = 8х2 – 7х +2. Репродуктивный уровень. 3. Исследовать функцию на выпуклость и найти точки перегиба у =ln(x2 + 4). Продуктивный уровень. 4.
Построить график ускорения точки, движение которой задано уравнением: S(t)
=
|
||
|
Вариант 5. Ознакомительный уровень. 1.Исследовать функцию на выпуклость и точки перегиба у = 4х3 + 6х. 2.Исследовать функцию на выпуклость и точки перегиба у = -х2 – 10х +5. Репродуктивный уровень. 3.
Исследовать функцию на выпуклость и найти точки перегиба у = Продуктивный уровень. 4.
Построить график ускорения точки, движение которой задано уравнением: S(t)
= t3
+ t2
+ t + 40, t Ответы: |
Вариант 6. Ознакомительный уровень. 1.Исследовать функцию на выпуклость и точки перегиба у = -9х3 + 4х. 2.Исследовать функцию на выпуклость и точки перегиба у = -2х2 + 6х +2. Репродуктивный уровень. 3.Исследовать функцию на выпуклость и точки перегиба
у = Продуктивный уровень. 4.Построить
график ускорения точки, движение которой задано уравнением: S(t)
= 2t3
+ 3t2
+ 5t – 1, t
|
||
|
Вариант 1. |
Вариант 2. |
Вариант 3. |
|
|
1.(0;0) 2.(0;8) Выпукла
при х Вогнута
при х |
1.(0;0) 2.(0;2) Выпукла
при х Вогнута
при х |
1.(0;0) 2.(0;4) Выпукла
при х Вогнута
при х |
|
|
3.(-2; -2е-2) Выпукла
при х Вогнута
при х |
3.(1; Вогнута
при х Выпукла
при х |
3.( Выпукла
при х Вогнута
при х |
|
|
Вариант 4. |
Вариант 5. |
Вариант 6. |
|
|
1.(0;0) 2. .(0;2) Выпукла
при х Вогнута
при х |
1.(0;0) 2. .(0;5) Вогнута
при х Выпукла
при х |
1.(0;0) 2. .(0;2) Вогнута
при х Выпукла
при х |
|
|
3. Выпукла
при х Вогнута
при х |
3.Точек перегиба нет. Вогнута на D(y). |
3. Точек перегиба нет. Выпукла на D(y). |
|
Критерии оценки:
Практическая работа №5.
«Вторая производная. Приложение второй производной к исследованию функции».
«4» балла за выполнение 100 % заданий, выданных преподавателем, без существенных ошибок.
«3» балла за 70 % выполнения задания с несколькими несущественными ошибками.
«2» балла за 50% заданий или выполнение всех заданий с несколькими существенными ошибками.
«1» балл за выполнение всех заданий с существенными ошибками.
«0» баллов - невыполнение заданий.
Для того чтобы практическая работа была зачтена, студенту необходимо
набрать не менее 2 баллов.
Практическая работа №6.
«Нахождение наибольшего и наименьшего значений функции на промежутке».
|
Вариант 1. Ознакомительный уровень. 1.Найти
наибольшее и наименьшее значение функции у=х2-6х+1,х Репродуктивный уровень. 2.
Найти наибольшее и наименьшее значение функции y=6х2-х3
, х Продуктивный уровень. 3. Найти наибольшее и наименьшее значения функции у=2tgx – tg2x, х |
Вариант 2. Ознакомительный уровень. 1.Найти
наибольшее и наименьшее значение функции у=х2–4х+6, х Репродуктивный уровень. 2.
Найти наибольшее и наименьшее значение функции y=6х2–3х4–1,
х Продуктивный уровень. 3.
Найти наибольшее и наименьшее значения
функции у=
|
||
|
Вариант 3. Ознакомительный уровень. 1.Найти
наибольшее и наименьшее значение функции у=х2+5, х Репродуктивный уровень. 2.
Найти наибольшее и наименьшее значение функции y=3х2-2х3
, х Продуктивный уровень. 3.
Найти наибольшее и наименьшее значения
функции у=
|
Вариант 4. Ознакомительный уровень. 1.Найти
наибольшее и наименьшее значение функции у=х2+8, х Репродуктивный уровень. 2.
Найти наибольшее и наименьшее значение функции y=3х-х3
, х Продуктивный уровень. 3.
Найти наибольшее и наименьшее значения
функции у=sin2x,
х |
||
|
Вариант 5. Ознакомительный уровень. 1.Найти
наибольшее и наименьшее значение функции у=х2-10, х Репродуктивный уровень. 2.
Найти наибольшее и наименьшее значение функции y=-3х+х3,
х Продуктивный уровень. 3.
Найти наибольшее и наименьшее значения
функции у=cos2x,
х |
Вариант 6. Ознакомительный уровень. 1.Найти
наибольшее и наименьшее значение функции у=х2-12, х Репродуктивный уровень. 2.
Найти наибольшее и наименьшее значение функции у=х3+3х2-9х,
х Продуктивный уровень. 3.
Найти наибольшее и наименьшее значения
функции у=
|
||
|
Ответы: |
|
||
|
Вариант 1. |
Вариант 2. |
Вариант 3. |
|
|
1.унаим(1)=-4 унаиб(0)=1 |
1.унаим(1)=3 унаиб(0)=6 |
1.унаим(0)=5 унаиб(1)=6 |
|
|
2. унаим(0;6)=0 унаиб(4)=32 |
2.унаим(
унаиб( |
2.унаим(
унаиб( |
|
|
3.унаим(0)=0
унаиб( |
3.унаим(3)=2 унаиб(3)=1,5 |
3.унаим(6)=3 унаиб(8)=5 |
|
|
Вариант 4. |
Вариант 5. |
Вариант 6. |
|
|
1.унаим(0)=8 унаиб(1)=9 |
1.унаим(0)=-10 унаиб(1)=-9 |
1.унаим(0)=-12 унаиб(1)=-1 |
|
|
2. унаим(3)=-18 унаиб(1)=2 |
2. унаим(1)=-2 унаиб(3)=18 |
2. унаим(1)=-5
унаиб( |
|
|
3.унаим(
унаиб( |
3.у(
|
3.унаим(-2)=-0,25 унаиб(2)=0,25 |
|
Критерии оценки:
Практическая работа №6.
«Наибольшее и наименьшее занчение функции».
«4» балла за выполнение 100 % заданий, выданных преподавателем, без существенных ошибок.
«3» балла за 70 % выполнения задания с несколькими несущественными ошибками.
«2» балла за 50% заданий или выполнение всех заданий с несколькими существенными ошибками.
«1» балл за выполнение всех заданий с существенными ошибками.
«0» баллов - невыполнение заданий.
Для того чтобы практическая работа была зачтена, студенту необходимо
набрать не менее 2 баллов.
Раздел 4.
Дифференциал. Первообразная. Интеграл.
Студент должен:
знать:
· определение первообразной;
· определение неопределенного интеграла и его свойства;
· формулы интегрирования;
· способы вычисления неопределенного интеграла;
· определение определенного интеграла, его геометрический смысл и свойства;
· способы вычисления определенного интеграла;
· понятие криволинейной трапеции, способы вычисления площадей криволинейных трапеций с помощью определенного интеграла;
· вычисление пути по заданной скорости с помощью определенного интеграла;
уметь:
· находить неопределенные интегралы, сводящиеся к табличным помощью основных свойств и простейших преобразований;
· выделять первообразную, удовлетворяющую заданным начальным условиям;
· восстанавливать закон движения по заданной скорости, скорость по ускорению;
· вычислять определенный интеграл с помощью основных свойств и формулы Ньютона-Лейбница;
· находить площади криволинейных трапеций;
· решать простейшие прикладные задачи, сводящиеся к нахождению интеграла.
Практическая работа №7
«Нахождение неопределённых интегралов».
Найти неопределённые интегралы:
|
Вариант 1. Ознакомительный уровень.
2. Репродуктивный уровень. 3. Продуктивный уровень. 4. 5.
|
Вариант 2. Ознакомительный уровень.
2. Репродуктивный уровень. 3. Продуктивный уровень. 4. 5.
|
||
|
Вариант 3. Ознакомительный уровень.
2. Репродуктивный уровень. 3. Продуктивный уровень. 4. 5.
|
Вариант 4. Ознакомительный уровень.
2. Репродуктивный уровень. 3. Продуктивный уровень. 4. 5.
|
||
|
Вариант 5. Ознакомительный уровень.
2. Репродуктивный уровень. 3. Продуктивный уровень. 4. 5.
|
Вариант 6. Ознакомительный уровень.
2. Репродуктивный уровень. 3. Продуктивный уровень. 4. 5.
|
||
|
Ответы: |
|
||
|
Вариант 1. |
Вариант 2. |
Вариант 3. |
|
|
1.х3 + х4 – 5х + с 2.3ех+х9+с |
1.2х3 + 2х4 – 15х + с 2.6ех+х7+с |
1.11х3 +11х4 – 9х + с 2.0,5e2x+2x9+c |
|
|
3.- |
3. |
3.
- |
|
|
4. 5. |
4. 5. |
4. 5. |
|
|
Вариант 4. |
Вариант 5. |
Вариант 6. |
|
|
1.3x3+4x4+х+c 2.2x3+0,2e5x+c |
1.5х3+5х4-50х+с 2.-6cosx+5x+c |
1.х7+х5-13х+с 2.6sinx-3x+c |
|
|
|
3. |
3. |
|
|
4.-
5. |
4. 5. |
4. 5. |
|
Критерии оценки:
Практическая работа №7.
«Нахождение неопределённых интегралов».
«4» балла за выполнение 100 % заданий, выданных преподавателем, без существенных ошибок.
«3» балла за 70 % выполнения задания с несколькими несущественными ошибками.
«2» балла за 50% заданий или выполнение всех заданий с несколькими существенными ошибками.
«1» балл за выполнение всех заданий с существенными ошибками.
«0» баллов - невыполнение заданий.
Для того чтобы практическая работа была зачтена, студенту необходимо
набрать не менее 2 баллов.
Рубежный контроль.
Рубежный контроль проводится в форме контрольной работы. На выполнение работы отводится 90 минут.
Контрольная работа
«Приложение производной к исследованию функции».
Вариант 1.
Ознакомительный уровень.
1.Найти производную функции: у = ![]() .
.
2.Найти значение производной функции в точке ![]() : у =
: у =![]() ,
, ![]() = 1.
= 1.
3. Написать уравнение
касательной к функции в точке ![]() у = х2 + 6х
+ 5
у = х2 + 6х
+ 5![]()
Репродуктивный уровень.
4.Найти скорость и ускорение движения точки через две секунды от начала движения, если S = 3t2 + 4t3 + 8t + 2(м).
5. Угловой коэффициент касательной, проведенной к
графику функции ![]() в точке с
положительной абсциссой
в точке с
положительной абсциссой ![]() ,
равен 2. Найдите
,
равен 2. Найдите ![]() .
.
Продуктивный уровень.
6. Построить график функции: у = х3 - 4х + 3.
Вариант 2.
Ознакомительный уровень.
1.Найти производную функции: у = ![]() .
.
2.Найти значение производной функции в точке ![]() : у =
: у =![]() ,
, ![]() = 1.
= 1.
3. Написать уравнение
касательной к функции в точке ![]()
у = х2
+ 4х + 3, ![]()
Репродуктивный уровень.
4.Найти скорость и ускорение движения точки через две секунды от начала движения, если S = 2t2 + 2t3 + 3t + 5(м).
5. Угловой коэффициент касательной, проведенной к
графику функции у=х3+3х в точке с положительной абсциссой ![]() = 6. Найдите
= 6. Найдите ![]() .
.
Продуктивный уровень.
6. Построить график функции: у = х3 - 3х.
Вариант 3.
Ознакомительный уровень.
1.Найти производную функции: у = ![]() .
.
2.Найти значение производной функции в точке ![]() : у =
: у =![]() ,
, ![]() = 1.
= 1.
3. Написать уравнение
касательной к функции в точке ![]() у = 2х2 + 6х
у = 2х2 + 6х![]()
Репродуктивный уровень.
4.Найти скорость и ускорение движения точки через две секунды от начала движения, если S = t2 + t3 + 5t -1(м).
5. Найти угловой коэффициент касательной, проведенной к графику функции у=х2+6 в точке с положительной абсциссой 2.
Продуктивный уровень.
6. Построить график функции: у = -х3 + 3х.
Вариант 4.
Ознакомительный уровень.
1.Найти производную функции: у =![]() .
.
2.Найти значение производной функции в точке ![]() : у =
: у =![]() ,
, ![]() = -1.
= -1.
3. Написать уравнение
касательной к функции в точке ![]() у = х2 + 8х
+ 6
у = х2 + 8х
+ 6![]()
Репродуктивный уровень.
4.Найти скорость и ускорение движения точки через две секунды от начала движения, если S = 4t2 + 2t3 + 10t - 2(м).
5. Найти тангенс угла наклона касательной к графику функции у=х2-4 в точке х0=2.
Продуктивный уровень.
6. Построить график функции: у = х4 - 4х + 3.
Вариант 5.
Ознакомительный уровень.
1.Найти производную функции: у = ![]() .
.
2.Найти значение производной функции в точке ![]() : у =
: у =![]() ,
, ![]() = -1.
= -1.
3. Написать уравнение
касательной к функции в точке ![]() у = х2 + 2х
+ 1
у = х2 + 2х
+ 1![]()
Репродуктивный уровень.
4.Найти скорость и ускорение движения точки через две секунды от начала движения, если S = 2t2 + 2t3 + 10t + 5(м).
5. Найти угол наклона
касательной к графику функции у=lnx
в точке ![]() = 1.
= 1.
Продуктивный уровень.
6. Построить график функции: у = -х4 - 4х - 3.
Вариант 6.
Ознакомительный уровень.
1.Найти производную функции: у = ![]() .
.
2.Найти значение производной функции в точке ![]() : у =
: у =![]() ,
, ![]() = 1.
= 1.
3. Написать уравнение
касательной к функции в точке ![]() у = -х2 +
6х
у = -х2 +
6х ![]()
Репродуктивный уровень.
4.Найти скорость и ускорение движения точки через три секунды от начала движения, если S = t2 + t3 + t + 2(м).
5. Написать уравнение нормали в точке х0=1 к графику функции у=х2+4х.
Продуктивный уровень.
6. Построить график функции: у = -х4 +4х - 3.
|
Ответы: |
|
||
|
Вариант 1. |
Вариант 2. |
Вариант 3. |
|
|
1.12х3(х4 + 5)2 2.-12 3.у = 10х + 1 |
1. 20х4(х5 + 6)3 2.-8 3.у=6х+2 |
1. 48х3(4х4 + 1)3 2.-7,5 3. у=14х-8 |
|
|
4.68; 54 5.1 |
4.35; 28 5.1 |
4.21; 14 5.4 |
|
|
Вариант 4. |
Вариант 5. |
Вариант 6. |
|
|
1.8sin3xcosx 2.-1,5 3.y=14x-3 |
1.-3сos2xsinx 2.-0,5 3.у=10х-25 |
1. 2.-12 3.у=2х+6 |
|
|
4.50, 32 5.4 |
4. 42; 28 5.450 |
4.34; 20 5.у=- |
|
Критерии оценки:
Рубежный контроль.
Контрольная работа
«Приложение производной к исследованию функции».
«10» баллов выставляется студенту за выполнение 100 % заданий, выданных преподавателем, без существенных ошибок;
«9» баллов выставляется студенту за выполнение не менее 90 % заданий, выданных преподавателем, без существенных ошибок;
«8» баллов выставляется студенту за выполнение не менее 80 % заданий, выданных преподавателем, без существенных ошибок;
«7» баллов выставляется студенту за 70 % выполненных заданий с некоторыми несущественными ошибками;
«6» баллов выставляется студенту за 60% выполненных заданий или выполнение всех заданий с несколькими несущественными ошибками;
«5» баллов выставляется студенту за 50% выполненных заданий или выполнение всех заданий с несколькими несущественными ошибками;
«0» баллов выставляется студенту за невыполнение заданий.
Для того чтобы задание было зачтено, студенту необходимо набрать не менее 6 баллов.
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Калязинский колледж им. Н.М. Полежаева
УЧЕБНО-СПРАВОЧНОЕ ПОСОБИЕ
«ТЕОРЕТИЧЕСКИЙ СПРАВОЧНИК»
190604 Техническое обслуживание и ремонт автомобильного транспорта
151001 Технология машиностроения
080114 «Экономика и бухгалтерский учет (по отраслям)»
Калязин
2013 год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Справочник рекомендован для преподавателей математики и студентов 2 курса, обучающихся по специальностям 190604, 080114 и 151001; может быть использован при дистанционной форме обучения.
Справочник является частью методического обеспечения учебного процесса; составлен в соответствии с федеральными государственными образовательными стандартами СПО для специальностей 190604 Техническое обслуживание и ремонт автомобильного транспорта, 151001 Технология машиностроения, 080114 «Экономика и бухгалтерский учет (по отраслям)». Справочный материал направлен на приобретение практических навыков при решении прикладных задач и для оказания помощи студентам гуманитарных специальностей при подготовке к практическим и контрольным работам, а так же при подготовке промежуточной аттестации по предмету.
Учебно-справочное пособие. «Теоретический справочник»: «Математика» 2 курс 190604, 151001 и 080114)/ Старикова Наталия Валерьевна.
Калязин: ГБОУ СПО Калязинский колледж им. Н.М. Полежаева , 2013, – 6 с.
ПРЕДЕЛЫ
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ.
1. ![]() 2.
2. ![]()
НЕОПРЕДЕЛЁННОСТЬ
ВИДА: ![]()
1) Если степень числителя выше степени
знаменателя, то предел равен ![]() .
.
2) Если степень знаменателя выше степени числителя, то предел равен нулю.
3) Если старшие степени числителя и знаменателя равны, то предел равен отношению коэффициентов при старших степенях.
1)
![]() = -
= -![]() 2)
2)![]() = 0 3)
= 0 3) ![]() =
= ![]()
НЕОПРЕДЕЛЁННОСТЬ
ВИДА: ![]()
Чтобы устранить неопределённость данного вида необходимо разделить числитель и знаменатель дроби на х – а, где а – это то число, к которому стремится х.
![]()
![]()
ПЕРВЫЙ
ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ: ![]() =1.
=1.
1. ![]() (умножим
числитель и знаменатель на 3) =
(умножим
числитель и знаменатель на 3) =
= ![]()
2.![]()
ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ
ПРЕДЕЛ: ![]() е
е
1. ![]() (делим
числитель и знаменатель на 3) =
(делим
числитель и знаменатель на 3) =
= 
 =
= ![]() е
е![]()
![]()
ПРОИЗВОДНАЯ. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ.
|
ФОРМУЛЫ |
Определение. Производной функции f(x) в точке хо называется предел отношения приращения функции к приращению аргумента при
|
||
|
1. С/ = 0 2. (кх)/ = к 3. (кх+в)/ = к 4. (U+V)/ = U/+V/ 5. (U-V)/ = U/-V/ 6. (UV)/ =U/V+V /U (кU)/ = к(U)/ 7.
( 8.
9.(sinx)/ = cosx 10.
(cosx)/ = -sinx 11. (tgx)/ = 12.
(ctgx)/ = - |
13.(logax)/
= 14.(lnx)/
= 15.(lgx)/
= 16.( 17.(ах)/ = axlna 18.(arctgx)/
= 19. (arcctgx)/ = -
20.
(arcsinx)/ = -
|
||
|
Физический смысл производной. V = S' a = V'= S'' |
|||
|
Геометрический смысл производной. к = tg |
|||
|
Уравнение касательной y-y0 = f'(x0)(x-x0) |
|||
|
Уравнение нормали y-y0
= - |
|||
|
|
|||
|
Монотонность функции. 1.Найти область определения функции. 2.Найти производную функции. 3.Найти корни производной и точки, в которых производная не существует. 4.Наносим полученные точки на область определения функции. 5.Определяем знаки производной в каждом из полученных промежутков. 6.а) Если производная положительна на промежутке (а; в), то функция возрастает на промежутке (а; в). б) Если производная отрицательна на промежутке (а; в), то функция убывает на промежутке (а; в).
|
|||
|
Наибольшее и наименьшее значения функции. 1.Найти производную функции. 2.Найти точки, в которых производная равна нулю или не существует. 3.Проверить, какие из точек принадлежат данной области определения. 4.Найти значения функции в точках, принадлежащих области определения и на концах отрезка. 5.Из полученных результатов выбрать наибольшее и наименьшее значения. |
|||
|
Экстремумы функции. Выполнить все пункты предыдущего алгоритма. 7.Если при переходе через точку х0 производная изменяет свой знак с «-» на «+», то точка х0 – точка минимума. Если при переходе через точку х0 производная изменяет свой знак с «+» на «-«, то х0 – точка максимума. 8.Чтобы найти экстремумы, необходимо найти значения функции в точках экстремумов. |
Замечания. 1. График нечётной функции симметричен относительно начала координат. 2.График чётной функции симметричен относительно оси OY. 3. График общего вида не имеет симметрии (собственная ось симметрии в расчёт не принимается).
План исследования функции.
1. Находим область определения функции. 2.Исследуем функцию на чётность-нечётность и периодичность. 3.Находим точки пересечения графика с осями координат. 4. Находим промежутки возрастания и убывания функции. 5.Определяем экстремумы функции. 6. Определяем промежутки выпуклости графика функции и точки перегиба. 7. Дополнительные точки. 8. Строим график. |
||
|
Выпуклость графика функции. 1.Найти область определения функции. 2.Найти производную функции. 3. Найти вторую производную функции 3.Найти корни второй производной и точки, в которых вторая производная не существует. 4.Наносим полученные точки на область определения функции. 5.Определяем знаки второй производной в каждом из полученных промежутков. 6.а) Если вторая производная положительна на промежутке (а; в), то график функции имеет выпуклость вниз на промежутке (а; в). б) Если вторая производная отрицательна на промежутке (а; в), то график функции имеет выпуклость вверх на промежутке (а; в). 7. Точки, отделяющие выпуклую часть от вогнутой – точки перегиба. Найти значения функции в точках перегиба.
|
|||
|
|
|||
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.
|
1. 2.
6. 7. 8. 9. 10.
|
11.
16. 17. 18.
|
|
|
ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА: |
||
|
|
||
|
ПРАВИЛА ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР. |
||
|
1.
Площадь фигуры, ограниченной: f(x)
|
|
|
|
2.
Площадь фигуры, ограниченной: f(x)
|
|
|
|
3.
Площадь фигуры, ограниченной двумя функциями f(x)
|
|
|
|
4. Площадь фигуры, ограниченной функцией, изменяющей свой знак, вычисляется по формуле, которая составляется для каждого случая индивидуально с применением формул пунктов 1. и 2.
|
|
|
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Калязинский колледж им. Н.М. Полежаева
УЧЕБНО-СПРАВОЧНОЕ ПОСОБИЕ
«ГЛОССАРИЙ»
ЕН.01. Математика
190604 Техническое обслуживание и ремонт автомобильного транспорта
151001 Технология машиностроения
080114 «Экономика и бухгалтерский учет (по отраслям)»
Калязин
2013 год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Глоссарий рекомендован для преподавателей математики и студентов 2 курса, обучающихся по специальностям 080114, 190604 и 151001. Справочник может быть использован при дистанционной форме обучения.
Справочник является частью методического обеспечения учебного процесса. Глоссарий составлен для оказания помощи студентам при подготовке к практическим и контрольным работам, а так же для подготовки к промежуточной аттестации по предмету.
Учебно-справочное пособие «Глоссарий»: «Математика» 2 курс
(080114, 190604 и 151001)/ Старикова Наталия Валерьевна.
Калязин: ГБОУ СПО Калязинский колледж им. Н.М. Полежаева, 2013, – 10 с.
ГЛОССАРИЙ.
Аксиома – утверждение, содержащееся в формулировках основных
свойств простейших фигур, которое не доказывается.
Апофема – высота боковой грани правильной пирамиды.
Аргументы функции – величины из некоторого множества элементов
(называемого областью определения функции), которые являются исходными данными для функции и которым соответствуют значения функции.
Арифметический корень n-й степени из числа a – неотрицательное число, n-я степень которого равна a.
Арккосинус числа a – такое число из отрезка, косинус которого равен a.
Арккотангенс числа a – такое число из интервала, котангенс которого равен a.
Арксинус числа a – такое число из отрезка, синус которого равен a.
Арктангенс числа a – такое число из интервала, тангенс которого равен a.
Боковая поверхность призмы (площадь боковой поверхности) – сумма
площадей боковых граней.
Вектор – математическая абстракция объектов, характеризующихся
величиной и направлением (это направленный отрезок).
Высказывание – это языковое образование, в отношении которого имеет
смысл говорить о его истинности или ложности.
Высота конуса – перпендикуляр, опущенный из его вершины на плоскость основания. Осью прямого кругового конуса называется прямая, содержащая его высоту.
Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды
на плоскость основания.
Геометрия – это наука о свойствах геометрических фигур.
График функции f – множество всех точек (x; y) координатной плоскости,
где y = f (x), а x «пробегает» всю область определения функции f.
Графический метод – метод решения задачи линейного программирования, заданной на плоскости, т.е. содержащей только две переменные.
Двухгранный угол – фигура, образованная двумя плоскостями с общей
ограничивающей их прямой.
Десятичный логарифм – логарифм по основанию 10: lg x = log 10 x.
Диаметр шара – отрезок, соединяющий две точки шаровой поверхности
и проходящий через центр шара. Концы любого диаметра называются
диаметрально противоположными точками шара.
Диаметральная плоскость – плоскость, проходящая через центр шара.
Сечение шара диаметральной плоскостью называется большим кругом, а
сечение сферы – большой окружностью.
Дифференциальное исчисление – раздел математики, в котором изучаются производные и их применения к исследованию функций.
Доказательство – в логике и математике - цепь правильных умозаключений, ведущих от истинных посылок к доказываемым тезисам.
Достаточное условие – условие, достаточное для того, чтобы данное условие соблюдалось. Однако возможны и другие варианты, которые не входят
в утверждение, но для которых верно достаточное условие.
Достоверное событие – событие, которое обязательно произойдет, если
будет осуществлена определенная совокупность условий.
Единичная окружность – окружность радиуса 1 с центром в начале
координат.
Закономерность – устойчивая связь между измеряемыми параметрами,
полученная в результате проведения эксперимента (опыта). Закономерности
могут быть достоверными и случайными закономерностями.
Замкнутая область – область вместе с еѐ границей.
Значение функции f в точке x – число y, соответствующее числу x.
Иррациональные уравнения – уравнения, в которых под знаком корня
содержится переменная.
Испытание – наблюдение явления, опыт, эксперимент, которые можно
провести многократно.
Исход – событие, результат некоторого испытания, не разложимы на
другие составные части (результаты) этих испытаний. На основе понятия
элементарного исхода построена формула умозрительного подсчета
вероятностей.
Касательная плоскость к конусу – плоскость, проходящая через образующую конуса и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
Квадратный корень – корень второй степени.
Комбинаторика – раздел математики, изучающий дискретные объекты,
множества (сочетания, перестановки, размещения и перечисление элементов) и отношения на них (например, частичного порядка).
Конус (круговой конус) – тело, которое состоит из круга – основания
конуса, точки, не лежащей в плоскости этого круга, – вершины конуса и всех
отрезков, соединяющих вершину конуса с точками основания.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
Координаты вектора с началом в точке A1 (x1; y1; z1) и концом в точке
A2 (x2; y2; z2) – это числа (x2 – x1, y2 – y1, z2 – z1).
Корень n-й степени из числа a – такое число, n-я степень которого
равна a.
Куб – прямоугольный параллелепипед, у которого все рѐбра равны.
Кубический корень – корень третьей степени.
Линейные размеры (измерения) прямоугольного параллелепипеда –
длины его непараллельных рёбер.
Логарифм числа b по основанию a – показатель степени, в которую
нужно возвести основание a, чтобы получить число b.
Логарифмическая функция с основанием a – функция, заданная формулой
y = logа x.
Математическая модель – формальная схема реального объекта (процесса, проблемы), составленная с помощью математических обозначений, символов и соотношений.
Многогранник – такое тело, поверхность которого состоит из конечного
числа плоских многоугольников.
Многогранник, вписанный в шар – многогранник, все вершины которого
лежат на поверхности шара. Многогранник называется описанным около
шара, если все его грани касаются поверхности шара.
Множество – совокупность элементов (предметов, физических объектов
и т.п.), объединенных в единое целое по имеющимся у них свойствам (цвет,
размер, и т.п.).
Наклонная, проведѐнная из данной точки к данной плоскости, – любой
отрезок, соединяющий данную точку с точкой плоскости, не являющийся
перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости,
называется основанием наклонной. Отрезок, соединяющий основания
перпендикуляра и наклонной, проведенных из одной и той же точки,
называется проекцией наклонной.
Натуральный логарифм – логарифм по основанию е: ln x = logex.
Необходимое условие – условие, без которого данное утверждение несостоятельно. Однако могут существовать и другие варианты, для которых
необходимое условие соблюдается.
Нечѐтная функция – функция f, если для любого x из еѐ области определения f (–x) = – f (x).
Обратимая функция – функция, принимающая каждое свое значение в единственной точке области определения.
Общий перпендикуляр двух скрещивающихся прямых – отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них.
Объединение множеств А и В – множество, состоящее из всех элементов, которые принадлежат хотя бы одному из множеств А или В.
Объем (для простых тел) – это положительная величина, численное значение которой обладает следующими свойствами:
1. Если тело разбито на части, являющиеся простыми телами, то объем этого тела равен сумме объемов его частей.
2. Объем куба, ребро которого равно единице длины, равен единице.
Окрестность точки a – любой интервал, содержащий эту точку.
Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей
через его ось.
Ось правильной пирамиды – прямая, содержащая еѐ высоту.
Ось цилиндра – прямая, проходящая через центры оснований.
Отрезок – часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными еѐ точками.
Параллелепипед – призма, основание которой параллелограмм.
Параллельные плоскости – плоскости, которые не пересекаются.
Параллельные прямые – прямые, которые лежат в одной плоскости и не пересекаются.
Параллельный перенос в пространстве – такое преобразование, при котором произвольная точка (x; y; z) фигуры переходит в точку (x+a; y+b; z+c), где числа a, b, c одни и те же для всех точек (x; y; z).
Первообразная для функции f на заданном промежутке – функция F, если
для всех x из этого промежутка F (x) = f (x).
Пересечение (множеств) – множество, состоящее из элементов, принадлежащих строго и первому, и второму множествам.
Периодическая функция с периодом Т 0 – функция f, если для любого x из области значения этой функции в точках x, x –Т и x+Т равны, то есть
f (x+T) = f (x) = f (x–T).
Перпендикуляр, опущенный из данной точки на данную плоскость – отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости,
называется основанием перпендикуляра.
Перпендикулярные прямые – прямые, пересекающиеся под прямым углом.
Повторение n элементов в m ячейках – количество повторения любого числа n различных и/или одинаковых элементов в любом порядке m раз.
Повторения часто используются в теории кодирования данных.
Повторная выборка – выборка, при которой отобранный объект возвращается после проведения обследования обратно в генеральную совокупность.
Подмножество – множество элементов, целиком входящее в другое множество.
Постоянная – функция, которая на всей своей области определения имеет постоянное значение (например: y = 2). График постоянно – прямая линия, параллельная оси абсцисс.
Пирамида – многогранник, который состоит из плоского многоугольника
– основания пирамиды, точки, не лежащей в плоскости основания, – вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.
Пирамида, вписанная в конус – такая пирамида, основание которой есть
многоугольник, вписанный в окружность основания конуса, а вершиной
является вершина конуса.
Пирамида, описанная около конуса – пирамида, у которой основанием
служит многоугольник, описанный около основания конуса, а вершина
совпадает с вершиной конуса.
Планиметрия – это раздел геометрии, в котором изучаются фигуры на
плоскости.
Поверхность тела – граница тела.
Показательная функция с основанием a – функция, заданная формулой
y = (где a![]() 0, a
0, a ![]() 1).
1).
Полная поверхность призмы равна сумме боковой поверхности и площадей оснований.
Полупрямая или луч – это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной еѐ точки. Эта точка называется начальной точкой полупрямой. Различные полупрямые одной и той же прямой, имеющие общую точку, называются дополнительными.
Правильная пирамида – пирамида, основанием которой является правильный многоугольник, а основание еѐ высоты совпадает с центром этого многоугольника.
Правильный многогранник – выпуклый многогранник, грани которого являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число рёбер. Существует пять типов правильных выпуклых многогранников:
Призма – многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом,
Призма, вписанная в цилиндр – такая призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковыми ребрами –
образующие цилиндра.
Призма, описанная около цилиндра – призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковые грани касаются цилиндра.
Приращение независимой переменной (приращение аргумента) в точке x0 – разность x – x0, обозначается ![]() x.
x.
Приращение функции f в точке x0, соответствующее приращению x –разность f (x) – f (x0) = f (x0 + x) – f (x0).
Производная функции f в точке x0 – число, к которому стремится разностное отношение при x, стремящемся к нулю.
Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.
Прямой конус – если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.
Прямоугольный параллелепипед – прямой параллелепипед, у которого основанием является прямоугольник.
3. Равные тела имеют равные объемы.
Равновеликие тела – тела, имеющие равные объѐмы.
Радиус цилиндра – радиус его основания.
Размещения – размещениями из n элементов по m элементов (m < n)
называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.
Расстояние между скрещивающимися прямыми – длина их общего перпендикуляра.
Расстояние от прямой до параллельной ей плоскости – расстояние от любой точки этой прямой до плоскости.
Результат (испытания) – одно из возможных значений случайной величины, полученной в результате испытания. Если все закономерности и входящие в них величины достоверны (однозначны), то полученный результат будет достоверным и единственным.
Синус и косинус – числовые функции, заданные соответственно формулами y = sin x и y = cos x. Синусоида – график синуса.
Скалярное произведение векторов – это число
Скрещивающиеся прямые – прямые, которые не пересекаются и не лежат в одной плоскости.
Сочетания – сочетанием из n по k называется набор k элементов, выбранных из данных n элементов.
Степенная функция – функция, заданная формулой f (x) = ax .
Степень числа a ![]() 0 с
рациональным показателем r =
0 с
рациональным показателем r =![]() , где m – целое число, а n – натуральное число.
, где m – целое число, а n – натуральное число.
Стереометрия – раздел геометрии, в котором изучаются фигуры пространстве.
Сумма векторов (a1; a2; a3) и (b1; b2; b3) – это вектор (a1 + b1; a2 + b2;
a3 + b3).
Тангенс и котангенс – числовые функции, заданные соответственно формулами y = tg x и y = ctg x. Тангенсоида – график функции tgх.
Тело – конечная замкнутая область.
Тело вращения – объѐмное тело, возникающее при вращении плоской фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости.
Тело называется простым, если его можно разбить на конечное число треугольных пирамид.
Теория вероятностей – наука, изучающая общие закономерности случайных явлений массового характера.
Тетраэдр – треугольная пирамида. Пирамида называется n-угольной, если еѐ основанием является n-угольник.
Тождество – равенство выражений с одной или несколькими переменными, левая и правая части которого принимают равные значения при всех допустимых значениях переменных.
Треугольник – фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – сторонами.
Трехгранный угол (abc) – фигура, составленная из трех плоских углов (ab), (bc), (ac).
Угол в 1 радиан – это такой центральный угол, длина дуги которого равна
радиусу окружности.
Угол между прямой и плоскостью – угол между этой прямой и ее проекцией на плоскость.
Угол между скрещивающимися прямыми – угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым.
Формула – математическое описание физической закономерности, выраженное в виде уравнения и позволяющее однозначно определить результат исхода по входящим в формулу переменным.
Функция – математическое понятие, отражающее связь между элементами различных множеств. Более точно, это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Цилиндр – тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра.
Чѐтная функция – функция f, если для любого x из еѐ области определения
f (–x) = f (x).
Шар – тело, которое состоит из всех точек пространства, находящихся на
расстоянии, не большем данного растояния от данной точки. Эта точка называется центром шара, а данное расстояние радиусом шара.
Шаровая поверхность, или сфера – граница шара.
Шаровой сегмент – часть шара, отсекаемая от него плоскостью.
Шаровой сектор – тело, которое получается из шарового сегмента и конуса. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.
Шаровой слой – часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар.
Скачано с www.znanio.ru
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.