
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Московский государственный университет геодезии и картографии (МИИГАиК)
Б.В. Краснопевцев
Рекомендовано УМО по образованию в области геодезии и фотограмметрии в качестве учебного пособия для студентов
высших учебных заведений, обучающихся по направлению подготовки
120200 "Фотограмметрия и дистанционное зондирование" в соответствии с программой курса "Аэрокосмические методы и фотограмметрия" специальности "Картография"
Москва 2008
Краснопевцев Б.В. Фотограмметрия. - М.: УПП "Репрография" МИИГАиК,
2008. - 160 с.
Учебное пособие написано в соответствии с утверждённой программой курса "Аэрокосмические методы и фотограмметрия", рекомендовано кафедрой фотограмметрии и ученым советом факультета аэрокосмических съёмок и фотограмметрии Московского государственного университета геодезии и картографии (МИИГАиК).
Для студентов 3 курса специальности "картография". Ил. 53, табл. 10, список лит. - 3 назв.
Рецензенты: профессор кафедры фотограмметрии Московского государственного университета геодезии и картографии, д.т.н. А.Г.Чибуничев;
профессор кафедры картографии и геоинформатики МГУ им. М.В.Ломоносова, д.г.н. Б.А.Новаковский
Московский государственный университет геодезии и картографии
(МИИГАиК)
СОДЕРЖАНИЕ
Введение.....................................……....................................................................с. 6
В.1. Фотограмметрия и её применение в различных областях
деятельности человека..................................................................................6
В.2. Основные события в истории фотограмметрии.........................................7
В.3. Виды съёмок.................................................................................................11 В.4. Съёмочные системы....................................................................................12
В.5. Цифровые карты.….....................................................................................15
В.6. Основные элементы центральной проекции кадрового фотоснимка.....15
1. Стереоскопическое наблюдение и измерение снимков...................................17
1.1. Монокулярное и бинокулярное зрение......................................................17
1.2. Стереопара и стереоскопическая модель...................................................19
1.3. Условия получения стереопары и
способы наблюдения стереомодели..........................................................21
1.4. Рабочие площади снимка и стереопары.....................................................23
1.5. Способы стереоскопического измерения снимков...................................24
1.6. Точность наведения марки на точки стереомодели..................................25
2. Фотограмметрические приборы и системы......................................................27
2.1. Фотограмметрические приборы..................................................................27
2.2. Цифровая фотограмметрическая система..................................................29
3. Источники, влияющие на точность фотограмметрической обработки снимков………………………………...…………………...............30
3.1. Источники ошибок фотограмметрических измерений.........................…30
3.2. Источники, искажающие центральную проекцию
на реальном снимке.....................................................................................31
3.3. Дисторсия объектива фотокамеры......................................................…....34
3.4. Деформация изображения...................................................................……37
3.5. Смещения точек на снимке, вызванные его наклоном………………….39
3.6. Смещения точек на снимке, вызванные рельефом местности………….41
3.7. Сдвиг изображения в плоскости прикладной рамки фотокамеры..........42
3.8. Влияние сферичности Земли на фотограмметрические измерения........43
4. Системы координат и элементы ориентирования снимков............................46
4.1. Системы координат, применяемые в фотограмметрии............................46
4.2. Система координат цифрового снимка с началом в его плоскости........46 4.3. Система координат аналогового снимка с началом в его плоскости......48
4.4. Система координат снимка с началом в его центре проекции.
Элементы внутреннего ориентирования снимка.....................................48
4.5. Продольный и поперечный параллаксы ………………...........................49 4.6. Система координат объекта. Элементы внешнего ориентирования
снимка и пары снимков..............................................................................50
4.7. Системы координат модели объекта. Элементы взаимного
ориентирования пары снимков..................................................................53
4.8. Определение элементов внешнего ориентирования снимков
во время съёмки...........................................................................................54
5. Формулы преобразования систем координат...................................................56
5.1. Технологическая схема преобразования систем координат....................56
5.2. Преобразование координат из системы координат сканера в систему координат снимка с началом в его центре проекции.............57
5.3. Преобразование координат из систем координат стереопары
в систему координат объекта..................................................…...............58
5.4. Формулы направляющих косинусов..........................................................61
5.5. Преобразование координат из систем координат стереопары идеального случая аэросъёмки в систему координат объекта...............62
5.6. Причины появления продольного и поперечного параллаксов...............63
5.7. Формула превышений....…..........................................................................64
5.8. Формулы преобразования координат между системами координат
наклонного снимка и объекта....................................................................65
5.9. Преобразование координат из системы координат горизонтального
снимка в систему координат объекта........................................................66
5.10. Преобразование координат из системы координат наклонного снимка в систему координат горизонтального снимка, имеющих
общий центр проекции..............................................................................67
6. Теоретические основы геометрической модели объекта................................68
6.1. Принцип построения геометрической модели объекта............................68
6.2. Внутреннее ориентирование снимка..........................................................69
6.3. Условие и уравнение взаимного ориентирования пары снимков...........70 6.4. Аналитическое решение взаимного ориентирования...............................71 6.5. Уравнения внешнего ориентирования модели объекта.
Элементы внешнего ориентирования модели..........................................74
6.6. Аналитическое решение внешнего ориентирования модели...................75
6.7. Вычисление элементов внешнего ориентирования снимка.....................76
6.8. Точность определения координат точек объекта
по измерениям стереопары.........................................................................77
7. Технологические процессы при создании и обновлении карт по снимкам...80
7.1. Технологическая схема стереофототопографической съёмки.................80
7.2. Расчёт технических параметров топографической аэросъёмки..............83
7.3. Обновление топографических карт по снимкам.......................................86
7.4. Фотосхема.....................................................................................................89
8. Фототриангуляция...............................................................................................91
8.1. Назначение и классификация фототриангуляции.....................................91
8.2. Точки, включаемые в сеть фототриангуляции………………………......91
8.3. Принцип построения сети фототриангуляции
способом независимых моделей................................................................94
8.4. Построение, внешнее ориентирование и уравнивание
сети фототриангуляции способом связок.................................................98
8.5. Точность фототриангуляции и расчёт съёмочного обоснования..........101
9. Получение цифровой и графической информации
об объекте по снимкам......................................................................................103
9.1. Технологическая схема фотограмметрической
обработки стереопары...............................................................................103
9.2. Построение и ориентирование модели объекта......................................105
9.3. Цифровая модель рельефа местности......................................................107
9.4. Смысл трансформирования снимков.......................................................111
9.5. Принцип цифрового ортофототрансформирования снимков................112
9.6. Цифровое фототрансформирование снимков равнинной местности....115
9.7. Фотоплан.....................................................................................................116
9.8. Съёмка рельефа и контуров по модели объекта......................................118
10. Создание топографических карт по материалам
наземной стереофототопографической съёмки..............................................122
10.1. Особенности выполнения наземной
стереофототопографической съёмки.....................................................122
10.2. Полевые и камеральные работы.............................................................123
11. Создание карт по космическим снимкам........................................................125
11.1. Особенности космической съёмки.........................................................125
11.2. Виды космических траекторий...............................................................126
11.3. Ориентация оптической оси съёмочной системы в пространстве......127
11.4. Выбор расположения съёмочных сеансов на траектории полёта........129
11.5. Особенности фотограмметрической обработки
космических снимков..............................................................................131
11.6. Особенность обработки панорамных снимков………………………..133
11.7. Принцип радиолокационной съёмки…………………………………..135
12. Кадастровые картографические документы...................................................138
12.1. Краткая историческая справка о кадастре.............................................138
12.2. Виды кадастра. Кадастровые документы...............................................139
12.3. Кадастровые картографические документы,
их создание и обновление......................................................................141
13. Картографирование дна водных пространств и
съёмка водной поверхности………………………………………………….144
13.1. Требования к технологии создания топографических карт
поверхности дна водных пространств………………………………...144
13.2. Виды съёмок поверхности дна и водной поверхности….....................145
13.3. Определение глубин и характеристик волн по аэроснимку…………150
13.4. Определение по стереопаре глубин и координат точек дна…………150
13.5. Гидролокационная съёмка поверхности дна………………………….155
Рекомендуемая литература.....................................................................................157
Сокращения, принятые в топографо-геодезическом производстве...................158
Предметный указатель............................................................................................159
ВВЕДЕНИЕ
В.1. Фотограмметрия и её применение в различных областях
деятельности человека
Название дисциплины происходит от греческих слов photos (свет), gramma (запись) и metreo (измеряю), что в вольном переводе означает измерение изображений объектов, записанных с помощью света. Если хотят подчеркнуть, что при измерении использовалось объёмное изображение объекта, то на основе греческого слова stereo (пространственный) такие измерения называют стереоскопическими или стереофотограмметрическими.
Фотограмметрия позволяет определить по снимкам исследуемого объекта его форму, размеры и пространственное положение в заданной системе координат, а также его площадь, объём, различные сечения на момент съёмки и изменения их величин через заданный интервал времени.
Фотограмметрическая обработка снимков имеет следующие преимущества:
1) по снимкам объекта можно получить числовую информацию о нём такой густоты, какой практически невозможно достичь при непосредственных промерах;
2) числовую и графическую информацию об объекте можно получить, не вступая с ним в контакт, когда объект недоступен для человека или находится в среде, опасной для его жизни;
3) оператор-фотограмметрист находится в благоприятных для человека кабинетных условиях.
С учётом этого фотограмметрию используют в различных областях науки, техники и производства. Например:
- для определения деформаций сооружений и их отдельных частей, происходящих в ходе эксплуатации и с течением времени. Например, сравнение измерений, проведённых по стереопарам моста или подъемного крана, полученных до их нагрузки, во время нагрузки и после, позволяет определить их деформации в зависимости от веса нагрузки;
- для определения характеристик движущихся объектов: транспортных средств, ковша экскаватора, ракет, снарядов, элементарных частиц при проведении ядерных исследований и т.п.;
- при изысканиях железных и автомобильных дорог, трасс трубопроводов, линий электропередач и других линейных объектов;
- при гидротехнических, гляциологических, геологических, географических изысканиях и исследованиях;
- при реставрации памятников архитектуры, скульптурных монументов, уникальных предметов;
- для фиксации и составления плана дорожно-транспортного происшествия или места преступления;
- для определения по снимкам, полученным в электронном микроскопе, характеристик микрорельефа, например, полированных поверхностей;
- для лечения сетчатки глаз и установки контактных линз, изготовления зубных протезов, изучения внутренних органов человека и его внешней формы. Например, измерения фигуры космонавта по стереопарам, полученным до полёта, во время нахождения космонавта на орбитальной станции и после посадки, позволяют составить подробную картину изменений, происходящих в теле человека в связи с перераспределение крови и жидкости под влиянием земного притяжения и невесомости. Эту же методику можно использовать при пошиве одежды с учётом индивидуальных особенностей строения тела человека.
Можно привести и другие примеры использования фотограмметрии, однако, учитывая, что курс лекций по этой дисциплине читается студентам картографической специальности, в учебном пособии описывается использование фотограмметрической обработки снимков применительно к созданию карт и планов местности.
В.2. Основные события в истории фотограмметрии
Появлению фотограмметрии предшествовал многовековой период возникновения и совершенствования графического способа получения перспективных изображений местности и преобразования их в план. Для этого использовалась камера-обскура (темная), являвшаяся прообразом фотокамеры. Описания работы с ней имеются в трудах Леонардо да Винчи (Leonardo da Vinci, 1500 г.) и немецкого астронома и математика И.Кеплера (J.Kepler, 1611 г.). Для удобства работы на свету была разработана камера-клара (светлая). Внутри камеры стояло поворачивающееся зеркало, которое отклоняло лучи либо вверх на матовое стекло, прикрытое козырьком, либо вниз через отверстие в дне камеры на полочку, прикреплённую снизу. Лист бумаги укладывался либо на матовое стекло, либо на полочку. Швейцарец М.А.Каппелер (M.A.Cappeler) в 1725 г. нарисовал две панорамные картины с целью составления карты горного массива Пилатус. Для этого он впервые использовал принцип пространственной засечки, названной впоследствии фотограмметрической. В 1759 г. немецкий математик И.Г.Ламберт (I.H.Lambert), используя принцип пространственной засечки, изложил теоретические основы перспективных изображений объектов. В 1791-1793 гг. на основе этих разработок французский гидрограф Ш.Ф.БотанБопре (Ch.F.Beautemps-Beaupre) провел съёмку камерой-клара территорий Вера Круз и Ван Дименсленд и составил планы с помощью разработанного им способа иконометрия (от греческого слова eikon - изображение). Однако требовался способ закрепления для длительного хранения изображения, полученного в камере-обскура. В 1839 г. француз Л.Ж.Дагер (L.J.Daguerre) и англичанин Ф.Талбот (F.Talbot) объявили о разработанных ими способах получения фотоизображений в камере-обскура, а английский астроном Д.Гершель (J.Herschel) впервые применил термин фотография. Дальнейшие достижения в фотографии и создании мобильных фотокамер открыли дорогу появлению фотограмметрии.
В 1852 г. французский топограф, инженер-майор Эмe Лосседа (Aime Laussedat) первым в мире выполнил фотосъёмку местности с целью создания по снимкам плана местности. С этого года начинается история фотограмметрии, хотя это название появилось позже. Э.Лосседа назвал свой способ метрофотография, т.е. измерительная фотография. Т.к. съёмка производилась для топографических целей, её назвали фототопографической. В 1858-1859 гг. под руководством Э.Лосседа с учётом набранного опыта была изготовлена первая в мире съёмочная система, приспособленная для наземных фототопографических съёмок и названная фототеодолит. Его конструкция представляла собой сочетание фотокамеры и теодолита.
В 1858 г. французский фотограф Ф.Турнашон (F.Tournachon), публиковавший свои статьи под псевдонимом Надар (Nadar), первым в мире выполнил фотосъёмку местности с воздушного шара. Он взял привилегию на воздушную фотосъёмку с целью определения границ земельных участков. Однако, столкнувшись со сложностями преобразования снимков в план, ограничился выполнением и рекламированием воздушной фотосъёмки.
В 1858 г. немецкий архитектор А.Мейденбауэр (F.Meydenbauer) использовал фотосъёмку для составления планов зданий и тем самым положил начало прикладному применению фотограмметрии, в данном случае в архитектуре. Он же предложил название фотограмметрия.
В России 18 мая 1886 г. первую фотосъёмку с воздушного шара произвел поручик А.М.Кованько (впоследствии генерал-лейтенант). В этом же году В.И.Срезневский создал первый в России фотоаппарат, предназначенный для воздушной фотосъёмки и являющийся прототипом аэрофотоаппарата. Этим фотоаппаратом 6 июля 1886 г Л.Н.Зверинцев произвел фотосъёмку с воздушного шара, управляемого А.М.Кованько. Они пролетели от СанктПетербурга до Кронштадта и отметили возможность изучения по воздушным фотоснимкам рельефа дна. В своем отчёте они написали, что наблюдали "прекрасную карту мелей, глубокой воды и фарватера".
В 1887-1889 гг. немецкий профессор К.Коппе (C.Koppe) создал фототеодолит, у которого впервые в мире на прикладной рамке были установлены координатные метки, которые закрепили на снимке координатную систему.
В начале 90-х годов XIX века инженер-поручик В.Ф.Найденов (впоследствии полковник, профессор Военно-инженерной академии (ВИА)) начал проводить работы с целью созданию планов местности по воздушным фотоснимкам и в 1907 г. написал первый русский учебник "Измерительная фотография и применение её к воздухоплаванию".
В 1891 г. инженер путей сообщений Н.О.Виллер впервые в России применил наземную фотосъёмку при изысканиях железных дорог на Кавказе.
В 1892 г. немец Ф.Штольц (F.Stolze) предложил для стереоскопических измерений снимков способ мнимой марки, который впоследствии стали использовать в большинстве стереофотограмметрических приборов, в том числе и на современных цифровых фотограмметрических системах, работающих на базе компьютеров.
В 1895-1896 гг. Ф.Н.Чернышев и академик Б.Б.Голицын провели наземные фототопографические съёмки на Новой Земле. В отчёте Б.Б.Голицын отметил, что по сравнению с мензульной съёмкой этот вид съёмки является сложным и неудобным, но он имеет преимущество во времени выполнения съёмки и в количестве измеряемых точек с одной постановки инструмента.
В конце 1896 г. и начале 1897 г. инженер МПС Р.Ю.Тиле находился в загранкомандировке, в которую его послали с целью изучения разработок в области фототопографии. Собранная информация была им издана в 1897 г. в трёх номерах журнала МПС, а затем в 1898 г. в брошюре "Практическая фототопография (фотограмметрия)". Сам Р.Ю.Тиле был назначен заведующим фототопографическими работами МПС. В 1908-1909 г.г. он издал трёхтомную монографию "Фототопография в современном развитии", в которой впервые в России в единой связности описал историю развития фотограмметрии, её теоретические основы, съёмочное и обрабатывающее оборудование, применение фотограмметрии в различных областях деятельности человека.
В 1898 г. для съёмки с воздушного шара поручик С.А.Ульянин создал фотокамеру под названием "телеаппарат", который в то время был наиболее совершенным и использовался в течение долгого времени.
В 1901 г. научный сотрудник немецкой фирмы Карл Цейсс (Carl Zeiss) К.Пулфрих (C.Pulfrich) разработал конструкцию стереокомпаратора, который до настоящего времени является самым высокоточным оптико-механическим стереофотограмметрическим прибором.
В 1908 г. австрийский военный топограф Э.Орел (E.Orel) на основе стереокомпаратора разработал конструкцию первого стереофотограмметрического прибора для составления топографических карт по наземным фотоснимкам и дал ему название "автостереограф". В сотрудничестве с К.Пулфрихом прибор был усовершенствован и под названием стереоавтограф серийно выпускался фирмой К.Цейсс в разных модификациях до 70-х гг. 20 века.
В России в 1910 г. были выполнены первые опытные фотосъёмки с самолёта лётчиками Севастопольской школы, а С.А.Ульянин создал первый в России фотоаппарат, предназначенный для съёмки с борта самолёта. В этом же году С.М.Соловьев опубликовал брошюру "О стереофотограмметрии".
В 1911 г. прошли первые испытания и с 1913 г. началась эксплуатация первого в мире полуавтоматического плёночного аэрофотоаппарата полковника В.М.Потте. Конструкция этого аэрофотоаппарата была в то время лучшей в мире, и он использовался у нас до конца 20-х гг.
В 1915 г. в Германии М.Гассер (M.Gasser) сконструировал двойной проектор, который был первым фотограмметрическим прибором для создания топографических планов и карт по аэрофотоснимкам. Однако он не нашел применения, т.к. не было использовано стереоскопическое наблюдение и измерение снимков. Наведение марки на точку производилось устранением двоения изображения точки на экранчике, перемещаемом по высоте. Этот прибор положил начало созданию нового класса приборов - универсальных стереофотограмметрических приборов (УСП), которые позволяли оператору выполнить все процессы, связанные со съёмкой плановой и высотной частей топографической карты по аэроснимкам.
В 1917 г. Р.В.Животовский написал "Курс аэрофотограмметрии", что указывает на смену термина "воздушная фотосъёмка" на аэрофотосъёмку.
В России в 1920 г. Н.М.Алексапольский начал чтение курса по фотограмметрии в Московском межевом институте (ММИ), а в 1921 г. на геодезическом факультете ВИА. В 1925 г. под руководством Н.М.Алексапольского в ММИ была организована кафедра фотогеодезии (с 1939 г. фотограмметрии). Он же с 1932 г. был первым заведующим кафедрой фотограмметрии в ВИА. Н.М.Алексапольский был энтузиастом внедрения аэросъёмки в топографическое производство и своими работами способствовал развитию контурно-комбинированной съёмки. Совместно с П.П.Соколовым Н.М.Алексапольский разработал фототрансформатор МГИ.
В разработку теории фотограмметрии и фотограмметрического приборостроения, кроме упомянутых соотечественников, свой вклад внесли Ф.В.Дробышев, А.С.Скиридов, Н.Я.Бобир, Н.Н.Веселовский, Н.А.Урмаев, М.Д.Коншин, Г.В.Романовский, А.Н.Лобанов, В.Б.Дубиновский, Р.П.Овсянников, Е.И.Калантаров и др. Ф.В.Дробышев создал линейку для построения координатной сетки, стереометр для рисовки горизонталей по стереопаре, стереограф для создания топографических карт по стереопарам аэроснимков и другие приборы. А.С.Скиридов получил авторские свидетельства (1927, 1929, 1933 гг.) на автоматическое вычерчивание горизонталей путём сравнения перемены плотностей фотоизображений вокруг соответственных точек на левом и правом фотоснимках. Только с появлением компьютеров данная проблема была частично решена. Н.Н.Веселовский был в числе первых, кто выполнял опытные производственные работы по аэросъёмке городов в крупных масштабах. Разработанные в ходе выполнения всех этих работ методики легли в основу последующих подобных съёмок. Н.А.Урмаев в 1941 г. опубликовал "Элементы фотограмметрии", где изложил теорию фотограмметрии с использованием векторной алгебры. Эта работа, стала основой для написания учебников и монографий по фотограмметрии. Труды М.Д.Коншина способствовали разработкам теории и технологии дифференцированного метода создания топографических карт. Его теория обработки аэроснимков с преобразованными связками проектирующих лучей позволила создать в середине 50-х гг. отечественные универсальные стереофотограмметрические приборы: стереопроектор и стереограф. Г.В.Романовский и Е.И.Калантаров разрабатывали самые современные для того времени фотограмметрические приборы, например, стереопроектор и автоматизированный стереокомпаратор. А.Н.Лобанов, В.Б.Дубиновский, Р.П.Овсянников своими работами способствовали внедрению в нашей стране аналитических методов обработки снимков с использованием вычислительной техники.
В 1957 г. канадский фотограмметрист Ю.В.Хелава (U.V.Helava) на 1-м Международном фотограмметрическом съезде сообщил о конструкции аналитического фотограмметрического прибора. Первый в мире образец этого прибора, созданный фирмами OMI (Италия) и Bendix (США) под названием АР-1 (analytical plotter), был продемонстрирован в 1960 г. Конструкция прибора состояла из измерительного блока, в качестве которого был использован стереокомпаратор, и электронно-вычислительной машины (ЭВМ). Программное обеспечение составил Ю.В.Хелава. Это было началом перехода фотограмметрии на использование компьютерной техники.
В 90-е годы ХХ века произошел полный переход на компьютерные технологии и цифровую обработку снимков, полученных различными съёмочными системами. Компьютер с программным пакетом полной обработки снимков стал цифровой фотограмметрической системой. Появился термин цифровая фотограмметрия и новые виды картографических документов - цифровая карта и цифровая модель местности, построенная по снимкам фотограмметрическими методами. Был создан высокоточный фотограмметрический сканер, преобразующий в цифровую форму снимки, полученные с помощью фотокамеры, с сохранением их геометрических, фотометрических и точностных характеристик. Фотокамеры уступают место цифровым фотокамерам, позволяющим вводить снимки в компьютер без использования сканера.
В.3. Виды съёмок
В зависимости от того, в какой среде производится съёмка, различают аэро-, наземную, космическую и подводную съёмки. Кроме того, виды съёмок различают в зависимости от того, в каких диапазонах электромагнитного и акустического спектров производится съёмка. Съёмку в пределах электромагнитного излучения (табл. В.1) производят в воздушной и безвоздушной средах. Таблица В.1.
|
Диапазон |
Область |
Зона |
Длина волны в мкм |
Вид съёмки |
|
Радио- |
|
свыше 1000 |
Радио- локационная |
|
|
Оптический |
Инфракрасная |
дальняя |
1000 - 7,00 |
Инфракрасная (тепловая) |
|
средняя |
7,00 - 1,70 |
|||
|
ближняя |
1,70 - 0,77 |
|||
|
Видимая |
красная |
0,77 - 0,62 |
Фотосъёмка |
|
|
оранжевая |
0,62 - 0,59 |
|||
|
жёлтая |
0,59 - 0,56 |
|||
|
зелёная |
0,56 - 0,50 |
|||
|
голубая |
0,50 - 0,48 |
|||
|
синяя |
0,48 - 0,45 |
|||
|
фиолетовая |
0,45 - 0,39 |
|||
|
Ультрафиолетовая |
ближняя |
0,39 - 0,30 |
Ультра- фиолетовая |
|
|
средняя |
0,30 - 0,20 |
|
||
|
дальняя |
0,20 - 0,01 |
|
||
|
Рентгеновский |
|
10-2 - 10-5 |
Рентгеновская |
|
Однако съёмку через атмосферу Земли можно производить только на следующих длинах волн, которые атмосфера пропускает:
- в оптическом диапазоне от 0,3 до 4,0 мкм, т.е. в ближней зоне ультрафиолетовой области, во всех зонах видимой области, во всей ближней и примерно в половине средней зонах инфракрасной области;
- в узких полосах второй половины средней и примерно половины дальней зонах инфракрасной области: от 4,5 до 5,5; от 7,9 до 13,2; от 17 до
28; 34; 350; 460 мкм;
- в радиодиапазоне - от 1 мм до 30 м.
Для картографических целей используют фотосъёмку в видимой области оптического диапазона. В дополнение к этой съёмке при создании тематических карт используют инфракрасную и ультрафиолетовую съёмки. Инфракрасная (тепловая) съёмка позволяет достаточно надёжно опознать объекты с учётом разности их температур. Съёмку в ближней инфракрасной зоне выполняют в дневное время. На снимках видны объекты, расположенные на земной поверхности. Съёмку в средней инфракрасной зоне выполняют ночью, чтобы исключить влияние солнечного излучения. В результате получают изображения, характеризующие распределение температур в поверхностных слоях земли и воды. Особенность съёмки в дальней инфракрасной зоне состоит в том, что её можно выполнять и днём, и ночью, т.к. солнечное излучение не оказывает влияния. Специфика ультрафиолетовой съёмки состоит в том, что обычные стекла поглощают практически почти все лучи этой области, пропуская только малую часть из ближней зоны. Поэтому для этой съёмки используют фотокамеру с объективом, линзы которого изготовлены из кварцевого стекла. Радиолокационная съёмка используется в том случае, когда объект не виден в оптическом диапазоне из-за плотных облаков или ночью. Такие условия существуют, например, на полюсах Земли, на планете Венера и некоторых других космических телах. Из-за пониженной разрешающей способности радиолокационных снимков этот вид съёмки используют при создании мелкомасштабных карт на большие площади. Рентгеновская съёмка применяется для съёмок прикладного характера, например, при исследовании внутренней структуры различных объектов.
В водной среде электромагнитные волны быстро гаснут, но хорошо распространяются акустические излучения (табл. В.2), ультразвуковой диапазон которых используют для производства гидролокационной съёмки с целью создания топографических и тематических карт дна водных пространств.
Таблица В.2.
|
Диапазон |
Длины волн |
Вид съёмки |
|
Инфразвуковой |
меньше 16 Гц |
- |
|
Слышимый человеком |
16 Гц - 20 кГц |
- |
|
Ультразвуковой |
свыше 20 кГц |
Гидролокационная |
В.4. Съёмочные системы
При съёмке применяют фотографические, оптико-электронные и цифровые съёмочные системы. В качестве приёмника светового потока используют фотоплёнку, светодиод, а в цифровых съёмочных системах прибор с зарядовой связью (ПЗС), который имеет форму матрицы или линейки.
Различают две формы записи изображения: аналоговую и цифровую. Цифровая форма записи очень удобна для хранения и обработки больших массивов изображений, обладает большой оперативностью, т.к. в отличие от аналоговой записи не требуется фотохимическая обработка фотоплёнки, отсутствуют процессы, связанные с изготовлением диапозитивов, по которым производят фотограмметрические измерения. Съёмка и обработка изображений может проходить почти одновременно.
По принципам построения изображения съёмочные системы делятся на кадровые и сканерные. К кадровым системам относятся фотокамеры, у которых все точки кадра фиксируются в один момент времени (в момент открытия затвора) на плоскости в центральной, перспективной проекции, что обеспечивает строгую геометрию построения изображения.
Принцип работы сканерных съёмочных систем заключается в том, что регистрация светового потока, идущего от объекта, производится либо построчно, либо поточечно.
Если регистрация выполняется построчно, то в один момент времени фиксируются все точки, составляющие строку кадра. Положения всех точек в строке будут получены из одного центра проекции и будут соответствовать центральному проектированию. Длина и ширина строки задаётся либо длиной и шириной узкой щели, пропускающей световой пучок и установленной перед фотоплёнкой, либо длиной и шириной линейки ПЗС. Развёртка изображения по кадру осуществляется по одному из двух способов: 1) отклонением светового пучка влево-вправо, перпендикулярно к направлению полёта, 2) движением съёмочной системы относительно объекта съёмки.
При первом способе, если съёмочная система и объект не смещаются относительно друг друга, то изображение получается в центральной проекции на цилиндрической поверхности. В этом случае прямые линии, перпендикулярные направлению панорамирования, будут изображаться прямыми, а прямые линии, параллельные панорамированию, - в виде кривых второго порядка. Это объясняется спецификой построения изображения на цилиндрической поверхности и не является искажением геометрии построения изображения. При фотограмметрической обработке таких снимков нужно использовать уравнения связи координат точек местности и их изображений в центральной проекции на цилиндрической поверхности. Если съёмочная система и объект смещаются относительно друг друга, то построение изображения происходит с искажением формы объекта. Эти особенности рассмотрены в п. 11.6.
При втором способе изображение будет получаться на плоскости в виде отдельного снимка со своим центром проекции, положение которого в пространстве будет отличаться от положений других центров проекции.
Если регистрация выполняется поточечно (бегущим лучом), то каждая точка изображения фиксируется в отдельный момент времени, имеет свой центр проекции, положение которого в пространстве будет отличаться от положений других центров проекции. Построение кадра осуществляется по двум вариантам: 1) последовательным фиксированием всех точек кадра, 2) последовательным фиксированием точек одной строки с развёрткой изображения по кадру за счёт линейного перемещения съёмочной системы относительно объекта или вращения съёмочной системы вокруг своей оси.
В качестве примера первого варианта можно привести телевизионную съёмку. Если телевизионная съёмочная система и объект взаимно не смещаются, то полученное изображение соответствует кадровой съёмке на плоскость в центральной проекции. Если же носитель перемещается, то изображение на экране электронно-лучевой трубки (ЭЛТ) или матрицы ПЗС тоже будет смещаться. Т.к. изображение считывается поточечно, то каждой точке на экране или матрице будет соответствовать свой центр проекции. Однако скорость считывания изображения большая, и если по сравнению с ней скорость смещения изображения по экрану или матрице мала, то изображение можно считать практически кадровым.
Второй вариант, например, был использован в оптико-механической сканирующей системе, которая устанавливалась на отечественных луноходах и автоматических станциях, проводивших съёмку 1) на поверхности Луны и Венеры, а также 2) с орбиты Луны. При съёмке на поверхности построение кадра происходило за счёт равномерного вращения съёмочной системы вдоль направления панорамирования. В результате при записи следующей строки оптический луч прибегал соседний участок местности. Таким способом можно записывать панораму с разворотом на 3600. При отсутствии линейного смещения съёмочной системы изображение получается в центральной проек-ции на сферической поверхности. При съёмке с орбиты разворот по кадру осуществлялся за счёт линейного смещения съёмочной системы. В резуль-тате изображение получалось на цилиндрической поверхности, но каждая строчка, как отмечалось выше, имела свой центр проекции. При отсутствии других движений носителя, кроме продольного линейного, центры проек-ций располагаются на оси цилиндрической поверхности.
В последние годы всё большее распространение получают лазерные сканерные системы, которые не только строят поточечно изображение объекта, но и фиксируют координаты точек изображения в съёмочной системе координат. Правда, пока эти системы находят применение при съёмке инженерных объектов, а не для создания топографических карт.
С точки зрения фотограмметрической обработки снимки, получаемые с помощью сканерных съёмочных систем, имеют сложную геометрию построения. Линейные и угловые перемещения такой съёмочной системы относительно объекта, неравномерность движения механических узлов вызывают смещения и развороты строк или точек относительно друг друга. Полностью учесть влияние всех этих факторов практически невозможно. В результате точность фотограмметрических измерений таких снимков и качество их дешифрирования ухудшаются по сравнению с кадровыми снимками. Это объясняет, почему подобные съёмочные системы не используют для создания и обновления топографических карт. Эти съёмочные системы применяют при космической съёмке, которая обеспечивает снимками картографирование в мелких масштабах (создание географических, обзорно-географических, тематических карт).
В.5. Цифровые карты
Техническая база аэрогеодезического производства позволяет создавать топографические карты в масштабах от 1:500 и мельче с помощью стереофототопографической съёмки по аэро-, наземным и космическим снимкам. Современные карты как топографические, так и географические создаются, хранятся, обновляются и передаются пользователям в цифровой форме. Прежняя графическая форма топографических карт используется по просьбе пользователя или по другим причинам. Основной конечной продукцией являются цифровая топографическая карта (ЦТК) и цифровой топографический план (ЦТП), а также цифровая топографическая фотокарта (ЦТФК), у которой информация в векторном виде наложена на растровое изображение местности. Базы данных цифровых карт формируются как трёхмерные массивы координат X, Y, Z объектов местности, сопровождаемые семантической информацией о каждом объекте. Цифровые карты позволяют создавать банки топографической и картографической информации, которая может быть использована многократно, полностью или частично по мере надобности. Такое возможно только при максимальном использовании компьютерной техники и цифровых методов обработки. Все это требует, чтобы области знаний фотограмметриста и картографа были сближены, дополняя друг друга.
В учебном пособии теория фотограмметрической обработки снимков и практические работы изложены на примере обработки кадровых аэроснимков. Обработка кадровых наземных и космических снимков, в основном, аналогична обработке аэроснимков, поэтому описываются только особенности их обработки. Радиолокационная и гидролокационная съёмки имеют специфические особенности. Обработка их данных отличается от фотограмметрической обработки снимков, поэтому изложены только общие принципы выполнения этих съёмок.
В.6. Основные элементы центральной проекции кадрового фотоснимка
Кадровый фотоснимок представляет собой изображение объекта на плоскости в перспективной, центральной проекции. Основные точки и линии этой проекции, используемые далее в тексте, показаны на рис. В.1 и даны их описания: где они располагаются и какие свойства имеют.
Р - плоскость наклонного снимка, картинная плоскость.
Е - горизонтальная (предметная) плоскость.
Р0 - плоскость горизонтального снимка, параллельная предметной плоскости.
S - центр проекции, в котором сходятся оптические проектирующие лучи. Из него получены наклонный Р и горизонтальный Р0 снимки.
SO - главный оптический луч наклонного снимка, перпендикуляр к
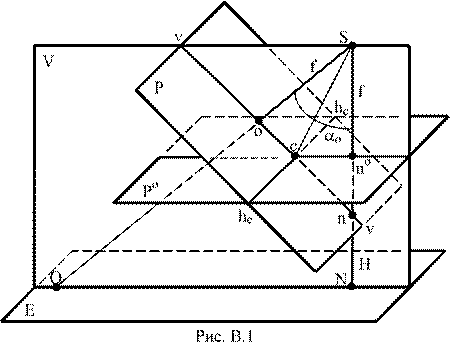
плоскости P.
о - главная точка наклонного снимка, точка пересечения главным оп-
тическим лучом SO плоскости P.
So = f - фокусное расстояние наклонного снимка.
SN - отвесная линия, перпендикуляр к горизонтальной плоскости Е.
Н = SN - высота фотографирования.
n - точка надира на наклонном снимке, точка пересечения этого снимка
отвесной линией SN. В точке надира сходятся изображения линий, перпендикулярных к плоскости Е (например, изображения деревьев, углов зданий). Расстояние этой точки от главной точки on = -f tg0.
n0 - главная точка горизонтального снимка, точка пересечения этого
снимка отвесной линией SN.
Sn0 = f - фокусное расстояние горизонтального снимка.
V - главная вертикальная плоскость, проведённая через главный оптический луч SO и отвесную линию SN.
vv - главная вертикаль наклонного снимка, линия пересечения этого
снимка плоскостью V.
oSn = 0 - угол наклона снимка P, определяет отклонение главного оптического луча SO от отвесной линии SN, лежит в плоскости V.
с - точка нулевых искажений, точка пересечения главной вертикали vv
и линии неискажённых масштабов hchc. Расстояние этой точки от главной точки как на наклонном, так и на горизонтальном снимках oc = -n0c = -f tg0,5о.
Sc - биссектриса угла 0. hchc - линия неискажённых масштабов, линия пересечения наклонного Р и горизонтального Р0 снимков.
1. СТЕРЕОСКОПИЧЕСКОЕ НАБЛЮДЕНИЕ И ИЗМЕРЕНИЕ СНИМКОВ
1.1. Монокулярное и бинокулярное зрение
Фотограмметрическая обработка снимков - измерение и дешифрирование - пока невозможна без использования зрения человека. Даже в будущем, когда возможно будет решена задача автоматической обработки снимков, за человеком останутся контрольные операции за работой приборов. В связи с этим кратко остановимся на особенностях зрения человека, который может наблюдать предметы монокулярно и бинокулярно.
Монокулярное зрение - наблюдение объектов одним глазом. Изображение объекта строится на сетчатке в перспективной, центральной проекции с помощью хрусталика, обеспечивающего резкость изображения путём изменения своей кривизны, что называется аккомодацией. Сетчатка глаза состоит из клеточек - колбочек (около 7 млн.) и палочек (до 130 млн.). Колбочки - органы дневного зрения, позволяющие воспринимать детали и цвет объекта. Палочки обладают очень высокой световой чувствительностью и обеспечивают наблюдение в сумерках и ночью, однако плохо передают детали и цвет объекта. Глаз воспринимает электромагнитные колебания в видимой области с длинами волн 0,39 - 0,77 мкм (см. таблицу В.1). Однако максимум цветовой чувствительности приходится на жёлтую зону (0,56 - 0,59 мкм), что примерно соответствует средней части видимой области. Поле зрения глаза в горизонтальной плоскости равно примерно 1500, а в вертикальной плоскости - примерно 1200.
Основная масса колбочек сосредоточена в жёлтом пятне, расположенном в центральной части сетчатки. Объекты, спроектировавшиеся на жёлтое пятно, наблюдаются наиболее чётко. Жёлтое пятно имеет овальную форму, вытянутую в горизонтальной плоскости ( 2 мм), и его поле зрения равно 6 - 70. В середине жёлтого пятна расположена центральная ямка, имеющая диаметр
0 около 0,4 мм (поле зрения 1,3 ) и состоящая только из колбочек. Диаметр колбочек здесь наименьший и лежит в пределах 1-5 мкм. Центральная ямка - наиболее чувствительное место глаза и при рассматривании какой-либо точки объекта человек поворачивает глаз так, чтобы её изображение оказалось в середине центральной ямки. Линия, проходящая через центр хрусталика и середину центральной ямки, называется зрительной осью. Расстояние вдоль зрительной оси от центра хрусталика до середины центральной ямки - фокусное расстояние глаза fГ 17 мм. Точка объекта, на которую направлена зрительная ось, называется точкой фиксации. Вокруг неё образуется поле ясной видимости, определяемое размером центральной ямки.
При монокулярном зрении две соседние точки человек видит раздельно, если они проектируются на отдельные клеточки сетчатки, разделённые нераздражённой клеточкой. Минимальный угол, при котором человек видит одним глазом две отдельные точки, составляет примерно 45" и называется остротой монокулярного зрения первого рода. При такой остроте зрения на расстоянии наилучшего зрения (250 мм) человек видит невооружённым глазом
45"х250 мм
две точки,
если расстояние между ними будет больше ![]() 0,055 мм 206265"
0,055 мм 206265"
или 55 мкм. При наблюдении линейных объектов минимальный угол составляет 20" и называется остротой монокулярного зрения второго рода. Повышение остроты зрения в этом случае объясняется тем, что линия проектируется на несколько клеточек, и тем самым повышается её восприятие головным мозгом. Поэтому в геодезии визирные марки и сетки нитей измерительных приборов имеют линейчатую форму. При монокулярном зрении человек уверенно оценивает положения объектов относительно друг друга влево и вправо, однако их отстояния определяет довольно приблизительно, опираясь на жизненный опыт, знание законов перспективы и различные косвенные признаки.
Бинокулярное зрение - наблюдение объектов двумя глазами (рис. 1.1).
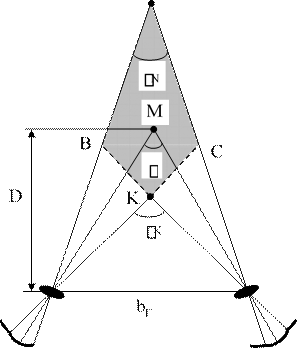 N Расстояние
между центрами хруста-
N Расстояние
между центрами хруста-
ликов глаз называется глазным базисом bГ. У людей величина глазного базиса колеблется в пределах 55 - 72 мм при среднем значении 64 мм. При рассматривании объекта наблюдатель выбирает точку фиксации (на рисунке точка М) и поворачивает глаза так, чтобы на неё были направлены зрительные оси обоих глаз. Угол , под которым пересекаются зрительные оси, называется углом конвергенции. Отстояние D точки, глазной базис bГ и угол конвергенции связаны зависимостью:
![]() k m
k m n Рис.
1.1 n' m'k' D
2tg( /bг 2) bг , (1.1)
где = 206265". При рассматривании точки на расстоянии наилучшего зрения
угол конвергенции 0 150. Максимальная величина угла конвергенции при на-
0 блюдении ближайшей точки равна 45 . Углы (k, n) между лучами, проектирующими остальные точки, называются параллактическими.
При рассматривании точек K и N, имеющих разные отстояния относительно точки фиксации M, их изображения проектируются на сетчатки левого и правого глаза по разные стороны относительно изображения точки фиксации. Дуги, расположенные слева от точки фиксации, считаются положительными, а справа - отрицательными. Разности дуг (mk - m'k' = k, mn - m'n' = n) являются физиологическими параллаксами, которые головной мозг преобразует в пространственные образы. Положительные физиологические параллаксы (например, k) вызываются ближними точками (точка К), а отрицательные (например, n) - дальними точками (точка N). При этом точки, спроектировавшиеся в центральные ямки глаз, попадают в зону ясного восприятия глубины, в пределах которой чётко воспринимается пространственный образ вокруг точки фиксации. Например, на рис. 1.1 вокруг точки М фиксации зоной ясного восприятия глубины будет участок, ограниченной линиями, соединяющими точки К, В, N и С (на рисунке участок заштрихован). Вне этого участка точки объекта воспринимаются двоящимися вдоль глазного базиса, т.к. изображения точек выходят за пределы центральных ямок и их физиологические параллаксы начинают превышать 0,35 мм (70′). Для проверки этого нужно перед собой держать на вытянутой руке авторучку и смотреть на какой-либо удалённый предмет. Авторучка будет восприниматься двоящейся. При переводе взгляда на авторучку удалённые предметы будут двоиться.
Минимальные физиологические параллаксы, при которых головной мозг еще фиксирует разность отстояний двух точек, зависят от освещённости, контрастности и формы объекты, усталости человека и т.д. В благоприятных условиях при наблюдении точечных объектов min = 2,5 мкм, а линейных объектов min = 1,0 мкм. Для перевода физиологических параллаксов в изменения параллактических углов используют формулу min = min/fг. В результате получаем, что для бинокулярного зрения при наблюдении точек min = 30" (острота первого рода), а при наблюдении линий min = 10" (острота второго рода).
Исходя из значений min и bГ = 64 мм, по формуле (1.1) можно вычислить радиус восприятия глубины DВГ = 440 м для точечных объектов и DВГ = 1100 м для линейных объектов. Т.к. окружающие нас предметы состоят из точечных и линейных элементов, то радиус пространственного восприятия примерно равен 700 - 800 м. Однако для разных людей это расстояние изменяется в ту или другую сторону, что объясняется субъективными особенностями зрительного аппарата и жизненным опытом. Например, геодезисты, имеющие опыт полевых измерений, гораздо точнее определяют расстояния до объектов, чем люди, не имеющие такого профессионального опыта. При отстояниях, превышающих DВГ, бинокулярное зрение строит картину местности, равнозначную наблюдаемым при монокулярном зрении. Радиус пространственного восприятия можно увеличить с помощью оптических приборов: бинокля, стереотрубы. Это объясняется тем, что они увеличивают глазной базис до размера В, определяемого их конструкцией, а также повышают остроту зрения за счёт увеличе-
B
ния наблюдательной
системы, т.е. DВГ = ![]() .
.
min
В заключение нужно отметить, что человек обладает восприятием глубины только в базисных плоскостях, т.е. плоскостях, проведённых через глазной базис и точки наблюдений. При нарушении этого условия человек будет наблюдать двоение точек в вертикальном направлении.
1.2. Стереопара и стереоскопическая модель
Использование восприятия человеком глубины при наблюдении и измерении снимков основано на том, что снимки построены по тем же законам перспективной, центральной проекции, что и изображения на сетчатках глаз. Два снимка, на которых изобразился один и тот же объект, называют стереоскопической парой или сокращённо стереопарой.
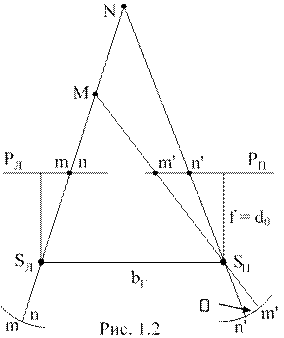 Предположим,
что из двух точек SЛ и SП (рис. 1.2), отстоящих друг от
друга на расстоянии, равном глазному базису bГ, были получены снимки
РЛ и РП фотокамерой с фокусным расстоянием f, равным
расстоянию наилучшего зрения d0. Если эти снимки установить перед
глазами человека в такие же положения, в которых они находились во время
съёмки, то точки снимков, являющиеся изображениями точек (М, N) объекта,
спроектируются на сетчатки глаз (m, n и m', n') человека так, как будто он
наблюдает этот объект. Разные отстояния точек M и N вызывают взаимные смещения
их изображений на снимках. Эти смещения (m'n') при рассматривании снимков
преобразуются в физиологические параллаксы
(см. п. 1.1),
Предположим,
что из двух точек SЛ и SП (рис. 1.2), отстоящих друг от
друга на расстоянии, равном глазному базису bГ, были получены снимки
РЛ и РП фотокамерой с фокусным расстоянием f, равным
расстоянию наилучшего зрения d0. Если эти снимки установить перед
глазами человека в такие же положения, в которых они находились во время
съёмки, то точки снимков, являющиеся изображениями точек (М, N) объекта,
спроектируются на сетчатки глаз (m, n и m', n') человека так, как будто он
наблюдает этот объект. Разные отстояния точек M и N вызывают взаимные смещения
их изображений на снимках. Эти смещения (m'n') при рассматривании снимков
преобразуются в физиологические параллаксы
(см. п. 1.1),
по величине и знаку которых головной мозг строит объёмный образ сфотографированного объекта. Наблюдаемое объёмное изображение называют стереоскопической моделью или стереомоделью. Изображения точки объекта на левом и правом снимках называют соответственными точками. Например, изображения точки М - точки m и m', а изображения точки N - точки n и n'.
Реальные условия получения снимков не соответствуют параметрам зрения человека. В результате стереомодель не будет подобна сфотографированному объекту. Её вертикальный масштаб 1:mB будет отличаться от горизонтального масштаба 1:m. Соотношение между масштабами определяется формуm 250
![]() лой:
. Например, при фокусном расстоянии фотокамеры f = 100 мм mв f
лой:
. Например, при фокусном расстоянии фотокамеры f = 100 мм mв f
стереомодель будет вытянута вверх в 2,5 раза, а при f = 350 мм будет сжата в 0,7 раз. Изменение увеличения наблюдательной системы не изменяет этот коэффициент, т.к. оно одновременно изменяет как горизонтальный, так и вертикальный масштабы. В то же время вытягивание рельефа на стереомодели облегчает его восприятие и рисовку горизонталей.
Другой особенностью стереомодели является то, что она вытягивается в сторону наблюдателя при перемещении головы человека влево-вправо относительно стереопары. Удаление (приближение) стереопары к глазам наблюдателя вызывает растяжение (сжатие) стереомодели. Небольшие развороты снимков относительно друг друга и относительно глаз человека приводят к наклонам и разворотам стереомодели в пространстве. Имеющиеся на снимках смещения точек, вызванные наклонами снимков и другими причинами, приводят к деформации стереомодели. Суммируя сказанное, нужно отметить, что стереомодель не является строгим подобием сфотографированного объекта. Т.к. на плановых снимках смещения точек, вызванные разными причинами, имеют сравнительно небольшие величины, наблюдаемая по этим снимкам стереомодель даёт, в целом, верное представление о рельефе местности.
|
Л |
|
|
|
П |
|
|
П |
|
Л |
|
 а) в)
а) в)
б)
Рис. 1.3
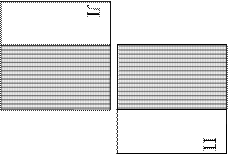
Кроме термина стереомодель, используется другой термин - стереоэффект. При рассматривании стереопары можно наблюдать прямой, обратный и нулевой стереоэффекты. Прямой стереоэффект возникает при рассматривании левого снимка левым глазом, а правого - правым (рис. 1.3, а, перекрывающиеся части покрыты сетчатым полем). Если снимки поменять местами (рис. 1.3, б), то физиологические параллаксы поменяют знак, и будет наблюдаться обратный стереоэффект, т.е., например, возвышенности будут восприниматься как
0 углубления. Если оба снимка повернуть на 90 и сместить вверх-вниз (рис. 1.3, в), то будет наблюдаться нулевой стереоэффект, т.е. два плоских изображения сольются в одно плоское. Это объясняется тем, что вдоль глазного базиса установятся ординаты точек, разности которых вызываются разным положением снимков в пространстве, а не рельефом местности.
Измерения стереопары выполняют при прямом стереоэффекте. Обратный стереоэффект можно использовать при измерении узкой глубокой долины. В этом случае дно долины будет восприниматься как водораздел и чисто психологически марку будет легче наводить на него.
1.3. Условия получения стереопары и способы наблюдения стереомодели
Для получения стереопары нужно выполнить три условия.
1. Снимки должны быть получены из разных точек пространства.
Условие является обязательным для получения измерительного стереоизображения.
2. Разномасштабность снимков не должна быть более 16%.
Если на приборе можно изменять масштабы изображений снимков относительно друг друга, то это условие не является обязательным.
3. При фотографировании объекта конвергенция главных оптиче-
0 ских осей съёмочных систем не должна превышать 15 .
Указанное значение соответствует углу конвергенции центральных оптических осей глаз при рассматривании точек на расстоянии наилучшего зрения. При фотосъёмке плоских объектов угол конвергенции оптических осей может быть и больше, но с увеличением рельефности объектов угол конвергенции нельзя брать большим, иначе на стереомодели появятся "мертвые зоны", в пределах которых не будет наблюдаться объёмное изображение. Кроме того, при большом угле конвергенции трудно наблюдать стереоэффект из-за больших перспективных искажений.
Для наблюдения по стереопаре объёмного изображения нужно выполнить два условия.
1. Каждый глаз должен рассматривать только один снимок. Чтобы выполнить данное условие, используют следующие способы.
Оптический способ основан на рассматривании снимков через оптические системы. Простой оптической системой является зеркально-линзовый стереоскоп, который можно использовать и при обработке снимков на компьютере. В этом случае стереоскоп устанавливают перед экраном, на который одновременно выводят оба снимка: левый снимок - на левую половину экрана, а правый снимок - на правую половину.
Анаглифический способ, предложенный Д'Альмейде в 1858 г., основан на том, что снимки проектируют на экран одновременно, но в разных цветах: левый снимок - в красном цвете, а правый снимок - в сине-зелёном цвете. Наблюдатель надевает очки, у которых перед левым глазом установлен красный светофильтр, а перед правым глазом - сине-зелёный светофильтр. В результате каждый глаз будет видеть снимок с соответствующей окраской, и оператор будет наблюдать объёмное изображение. Недостатки способа: 1) наличие очков (особенно, для людей, носящих очки, т.к. приходится одевать очки на очки); 2) светофильтры должны быть тщательно подобраны по частотным характеристикам как между собой, так и с соответствующими изображениями на экране. Если это не соблюдается, то каждый глаз видит слабое изображение соседнего снимка. В результате стереоскопическое изображение окажется окрашенным и нечётким; 3) потери света в светофильтрах; 4) при наблюдении цветных снимков происходит искажение цветовой гаммы. Способ применяют при печати объёмных (анаглифических) карт и открыток, а также чертежей в учебниках по геометрии. Этот способ используют при обработке снимков на компьютере.
У поляроидного способа, предложенного Ж.Андертоном в 1891 г., принцип получения стереоизображения такой же, как и у анаглифического способа, только используют поляроидные светофильтры с углом поляризации между
0 ними, равным 90 . Способ позволяет рассматривать чёрно-белые и цветные снимки. Недостатки способа: 1) наличие очков; 2) потеря света в поляроидах составляет 50%; 3) при отражении от экрана может происходить частичная деполяризация, что ухудшает стереоизображение. Данный способ применяют при просмотре стереокинокартин. Его можно использовать при обработке снимков на компьютере, но для этого нужен специальный монитор.
Способ чередования снимков (ранее назывался "обтюраторный способ", предложен Д'Альмейде в 1858 г.) основан на поочередном проектировании снимков на экран. С такой же частотой синхронно открывается левая или правая ветви наблюдательной системы. Для рассматривания стереоизображения применяют очки с фильтрами на жидких кристаллах, так называемые "затворные очки". Недостатки способа: 1) наличие очков; 2) потеря света в фильтрах. Этот способ является основным при обработке снимков на компьютере. Его можно применить и в бытовом стереотелевидении.
При растровом способе, предложенном Бертье и Лизегангом в 1896 г., два снимка проектируют на экран, составленный из линз цилиндрической формы. Оптические лучи, несущие изображения левого и правого снимков, отражаются противоположными гранями линз и попадают в соответствующие глаза наблюдателя. Недостатки способа: 1) из-за интерференции световых лучей нарушается равномерность освещения по полю стереоизображения; 2) ограничение размеров стереоизображения. Данный способ используют при безочковом просмотре стереокинокартин, а также при изготовлении объёмных открыток. В фотограмметрии этот способ не нашел применения.
2. Разделив снимки по глазам тем или иным способом, необходимо их развернуть в своих плоскостях так, чтобы линии, соединяющие соответственные точки на обоих снимках, были параллельны глазному базису.
1.4. Рабочие площади снимка и стереопары
Съёмку контуров и рельефа производят не по всей его площади, т.к. геометрия построения и качество изображения ухудшаются по мере смещения от центра к краю снимка. Кроме того, снимки перекрывают друг друга, и нет смысла приближаться к краю снимка, когда эта область на соседнем снимке расположена ближе к центру. Учитывая это, выделяют рабочие площади снимка и стереопары, в пределах которых вычерчивают контуры и горизонтали, а на границах соседних рабочих площадей выполняют их сводку.
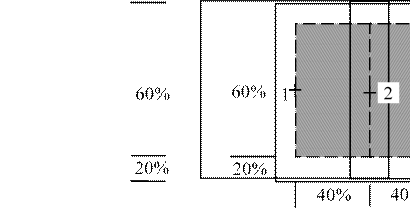
Рабочая площадь снимка (на рис. 1.4, а она заштрихована) это его цен-
|
|
|
|
|
|
|
|
|
|
|
|
|
30% |
40% |
30% |
 20% 20%
20% 20%
а. Рис. 1.4 б.
тральная часть, ограниченная линиями, проходящими посредине продольных и поперечных перекрытий. При 60% продольном и 40% поперечном перекрытиях линии будут проходить от краев снимка на расстояниях, равных 30% и 20% от длины стороны снимка, соответственно. Следовательно, рабочая площадь будет иметь форму прямоугольника, вытянутого в поперечном направлении, со сторонами, составляющими 40% и 60% от длин сторон снимка. При формате снимка 18х18 см рабочая площадь имеет размеры 72х108 мм, а при формате снимка 23х23 см - 92х138 мм.
Рабочая площадь стереопары это центральная часть продольного перекрытия двух снимков, ограниченная линиями, проходящими посредине поперечных и тройных продольных перекрытий. На рис. 1.4, б изображены три снимка: 1, 2 и 3, составляющие соседние стереопары. Стереопары перекрываются в пределах зоны тройного продольного перекрытия снимков, где находится главная точка снимка 2. Следовательно, левые и правые границы рабочих площадей стереопар должны проходить примерно через центральные точки 1, 2 и 3-го снимков. При продольном перекрытии 60% расстояния между ними составляют 40% от длины продольной стороны снимка. Верхняя и нижняя границы рабочих площадей стереопар при поперечном перекрытии 40% проходят от соответствующих краев снимков на расстояниях, составляющих 20% от длины стороны снимка. При формате 18х18 см размеры рабочей площади стереопары будут равны 72х108 мм, а при формате 23х23 см - 92х138 мм.
1.5. Способы стереоскопического измерения снимков
Для стереоскопического измерения снимков используют два способа: мнимой марки и реальной марки.
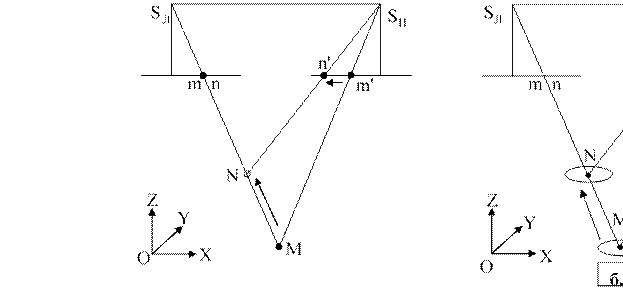
Способ мнимой марки (рис. 1.5, а), предложенный Ф.Штольцем (Герма-
 а. Рис. 1.5
а. Рис. 1.5
ния) в 1892 г., основан на том, что на каждый снимок стереопары проектируется одинаковое изображение измерительной марки. В результате наблюдатель каждым глазом видит участок снимка с маркой. Т.к. марки имеют одинаковую форму, размер и цвет, то при приближении к соответственным точкам они сливаются в одну мнимую стереоскопическую марку. При совмещении марок с соответственными точками (m и m') стереоскопическая марка будет восприниматься лежащей на поверхности стереомодели в точке М. При смещении, например, правой марки с точки m' на точку k' стереоскопическая марка будет восприниматься перемещающейся по высоте в пространстве стереомодели с точки М на точку К. Следовательно, перемещая обе марки по снимкам и совмещая их с соответственными точками, можно измерить координаты точек в пространственной системе координат модели. Этот способ применяется в большинстве фотограмметрических приборов и систем.
Способ реальной марки (рис. 1.5, б), предложенный канадским фотограмметристом Е.Девилем (E.Deville) в 1902 г., заключается в том, что в пространство стереомодели вводится экран, имеющий в центре светящуюся точку, которая служит реальной измерительной маркой. Экран перемещается вдоль трёх координатных осей и при совмещении марки с точкой стереомодели фиксируются её координаты в системе координат модели. Этот способ не нашел широкого применения в фотограмметрии и использовался только в некоторых фотограмметрических двух- и многокамерных проекторах.
Измерительная марка имеет форму точки, кольца или креста. Точка и кольцо, в основном, использовались в оптико-механических приборах, а в ЦФС преимущественно применяют крест. Размер марки изменяют в зависимости от увеличения наблюдательной системы. Размеры марок в каждой ветви наблюдательной системы не должны отличаться более чем на 10%. Цвет марки устанавливают в зависимости от цвета снимков. При измерении чёрно-белых снимков цвет марки лучше устанавливать жёлтый или светло-зелёный, т.к. эти цвета позволяют хорошо наблюдать марку на темных участках и не утомляют глаза. На светлых участках можно использовать синий цвет. При использовании анаглифического способа наблюдения объёмного изображения цвет марки должен быть жёлтый, белый или чёрный.
1.6. Точность наведения марки на точки стереомодели
Стереоскопическое наблюдение и измерение пары снимков даёт возможность получить результаты с большей достоверностью и более высокой точностью, чем при монокулярном наблюдении и измерении каждого снимка стереопары в отдельности. Это объясняется тем, что острота стереоскопического зрения в полтора-два раза выше (см. п. 1.1). Кроме того, если на одном из снимков какая либо точка объекта по каким либо причинам не изобразилась, но она имеется на другом снимке, то на стереомодели эта точка также будет видна. В результате по стереомодели повышается опознаваемость точек и дешифрируемость контуров, а также становится более надёжным процесс наведения измерительной марки на наблюдаемые точки.
Точность совмещения измерительной марки с наблюдаемой точкой зависит от ряда факторов: остроты зрения, увеличения наблюдательной системы прибора, освещённости и контрастности снимков, размера, цвета и освещённости обеих марок, степени утомлённости наблюдателя и других. При бинокулярном наблюдении стереопары человек видит каждым глазом точки снимка и измерительную марку в виде точки (у креста измерительной частью является точка пересечения лучей). Соответственные точки обоих снимков сливаются в точку стереомодели, а обе измерительные марки - в одну стереоскопическую марку. Таким образом, наблюдатель должен совмещать две точки в плане и по высоте. Величины несовмещения двух марок в одну, а также величины планового несовмещения стереоскопической марки с точкой стереомодели определяются остротой бинокулярного зрения первого рода min = 30" и могут быть вычислены по формуле
![]() 250 min ,
(1.2)
250 min ,
(1.2)
xy =
где = 206265", а - увеличение наблюдательной системы прибора. Согласно формуле (1.2) при увеличениях 8-10х точность совмещения стереоскопической марки с точками стереомодели в плане будет xy 4 - 5 мкм. Поскольку в момент совмещения стереоскопической марки с точкой стереомодели фиксируются продольный и поперечный параллаксы, их точность измерения будет такой же, т.е. p q 4 - 5 мкм.
Величина несовмещения по высоте z стереоскопической марки с точкой стереомодели рассчитывается по формуле
![]() z = 2502 min .
(1.3)
z = 2502 min .
(1.3)
bг
Подставив в (1.3) min = 30", bГ = 64 мм, = 10х получим, что стереоскопическое совмещение измерительной марки с точкой стереомодели выполняется с
z 1
![]() ошибкой z = 14 мкм или с относительной
ошибкой .
25000 18000
ошибкой z = 14 мкм или с относительной
ошибкой .
25000 18000
С переходом на компьютерную обработку снимки вводят в компьютер в цифровой форме. Точность измерения цифровых снимков определяется размером пиксела, с которым снимки были получены в цифровой фотокамере или было выполнено сканирование фотоснимков. Чтобы сохранить качество и точность фотоснимка нужно, чтобы размер пиксела соответствовал его разрешающей способности. Например, при разрешающей способности фотоснимка 1
R = 25 л/мм
размер пиксела должен быть
= ![]() =
0,02 мм. При сканировании 2R
=
0,02 мм. При сканировании 2R
снимков размер пиксела определяется установкой числа пикселов (dpi) в одном дюйме (25,4 мм). При размере пиксела 0,02 мм число пикселов в одном дюйме должно быть равно 1270. Если при выводе снимка на экран монитора пиксел снимка будет совмещаться с пикселом монитора, то точность наведения марки на точки снимка будет находиться в пределах одного пиксела. С целью увеличения размера изображения на экране монитора исходный пиксел заменяют матрицей nxn пикселов. В этом случае точность наведения марки повышается до 1/n размера исходного пиксела. Более подробно об этом в 4.2.
Конечный результат фотограмметрической обработки снимков зависит не только от точности наведения марки на точки снимков, но и от описанных в главе 3 источников, снижающих точность фотограмметрических измерений.
2. ФОТОГРАММЕТРИЧЕСКИЕ ПРИБОРЫ И СИСТЕМЫ
2.1. Фотограмметрические приборы
В 19 веке начали создавать фотограмметрические приборы для преобразования и измерения снимков. Их конструкции состояли как из механических деталей, так и из оптических систем.
Простым фотограмметрическим прибором является зеркальный стереоскоп, изобретённый в 1832 г. Ч.Уитстоуном (Ch.Wheatston), т.е. ещё до изобретения фотографии в 1839 г. В настоящее время используется зеркальнолинзовый стереоскоп, каждая оптическая ветвь которого состоит из двух зеркал и линзы. Есть стереоскопы со сменными линзами или окулярами, позволяющими менять увеличение в каждой ветви независимо и тем самым рассматривать разномасштабные снимки. Совместно со стереоскопом используют измерительный прибор параллаксометр, позволяющий измерить высоты небольших объектов (деревьев, домов малой этажности и др.).
В нашей стране для дешифрирования снимков и измерения продольных параллаксов с помощью встроенного параллаксометра используют стационарный прибор Interpretoskop (интерпретоскоп) немецкой фирмы К.Цейсс. Существуют две модификации прибора: с одной бинокулярной головкой и двумя. Два бинокуляра позволяют двум дешифровщикам одновременно рассматривать стереопару. Изменение увеличения в каждой ветви наблюдательной системы производится независимо и плавно в двух диапазонах: 2-6 и 5-15х. Можно рассматривать неразрезанные фильмы и отдельные снимки на прозрачной или непрозрачной основах.
Имеются стереоочки, у которых вместо линз в оправе закреплены призмы, поворачивающие оптические лучи до положения, когда они становятся параллельными. Однако такие очки не получили широкого распространения.
До конца 20 века были созданы различные оптико-механические фотограмметрические приборы, но в начале 21 века они полностью уступили место компьютерной технике. Практически весь 20 век, просуществовал стереокомпаратор (СК), предназначенный для измерения координат и параллаксов точек стереопары с инструментальной точностью 2-5 мкм. Во второй половине 20 века СК был использован при создании аналитического фотограмметрического прибора (АФП). В нём СК, исполнявший функцию измерительного блока, был соединён с электронно-вычислительной машиной (компьютером). Такие приборы были созданы в разных странах. В нашей стране были разработаны стереопроектор аналитический (СПА) и стереоанаграф. В 90-е годы была приобретена у фирмы Leica (Швейцария) лицензия на выпуск её прибора SD 2000 под названием SD 20. Ряд организаций использовали Traster (трастер) фирмы Matra (Франция). Его особенностью является то, что оператор рассматривает объёмное изображение на стеклянном экране, используя очки с поляроидными светофильтрами. Кроме того, каретки, несущие снимкодержатели, перемещаются на воздушной подушке по отполированной гранитной плите, что делает их движения очень чувствительными.
На рис. 2.1 показана примерная блок-схема АФП. Пара снимков устанав-
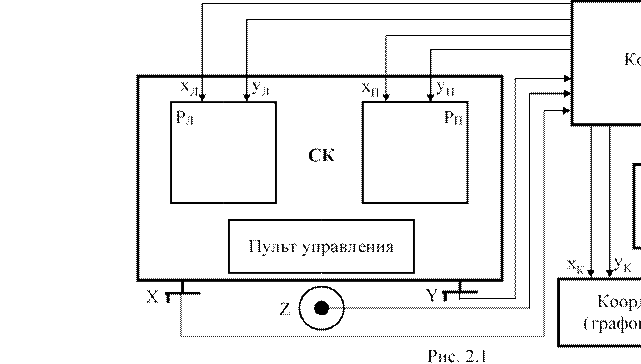
ливается в снимкодержатели Рл и Рп измерительного блока (СК). Оператор, наблюдая точки снимков, вращает штурвалы X, Y, Z, с которыми связаны датчики, преобразующие вращательное движение в кодированные электрические импульсы. Последние поступают в компьютер, где по заданной программе происходит преобразование вводимых значений координат из системы координат сфотографированного объекта в координаты xЛ, yЛ, xП, yП соответственных точек снимков в системе координат прибора. Согласно их значениям компьютер вырабатывает управляющие электрические импульсы на электромоторы, которые смещают каретки со снимкодержателями. Пульт управления в виде клавиатуры оператор использует для включения нужной программы и управления работой всех блоков, входящих в систему. Регистрация результатов выполняется на магнитном или лазерном диске.
К компьютеру подключается принтер, на котором печатаются номера и координаты точек в заданной системе координат, а также все значения промежуточной обработки снимков. При подключении принтера с высоким разрешением можно печатать фотопланы, но можно для этой цели подключить фотопечатающее устройство. Можно подключить координатограф (графопостроитель), на котором в заданной картографической проекции вычерчивается графический план.
Инструментальная точность АФП при измерении плановых координат равна 2-3 мкм в масштабе снимка, а ошибка измерения высот меньше Н/10000, где Н - высота фотографирования.
Т.к. на АФП можно было учитывать систематические ошибки, характер действия которых описывался математическими зависимостями, эти приборы позволили не только повысить точность обработки снимков, но и открыли возможности использования снимков, полученных не измерительными фотокамерами. При обработке космических снимков АФП позволили относительно быстро создавать карты в разных картографических проекциях и масштабах.
Появление компьютеров с большими объёмами памяти и высокой скоростью счёта, достижения в области компьютерной графики и цифровых методов записи изображений привели к созданию нового типа фотограмметрической техники - цифровой фотограмметрической системы (ЦФС), которая к началу 21 века полностью вытеснила аналоговые приборы и частично АФП.
2.2. Цифровая фотограмметрическая система
ЦФС конструктивно представляет серийно выпускаемый персональный компьютер (рис. 2.2), в память которого введены программы, обеспечивающие
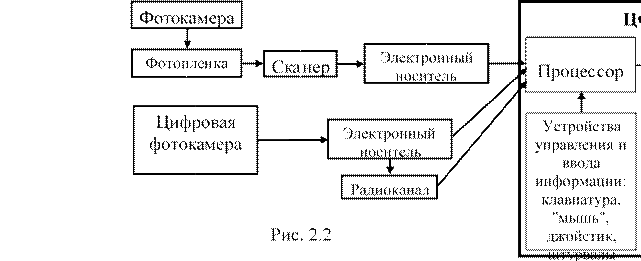
выполнение всех фотогр амметрических процессов, необходимых для создания цифровой карты по цифровым снимкам. Для наблюдения стереоскопической модели сфотографированного объекта на экране монитора используют способы, описанные в п. 1.3, но пока основным является способ чередования снимков с использованием затворных очков.
Введение в ЦФС снимков возможно двумя путями: либо предварительно преобразовав фотоснимок в цифровую форму с помощью фотограмметрического сканера, либо с цифровой фотокамеры. С электронного носителя цифровой фотокамеры снимки можно передавать по радиоканалу во время съёмки или же после съёмки переписать в компьютер.
В нашей стране используют как отечественные ЦФС (ЦНИИГАиК, Photomod, Талка и др.), так и зарубежные. Все ЦФС, в основном, соответствуют друг другу, имея преимущество в отдельных видах обработки снимков. На ЦФС по наземным, аэро- и космическим снимкам создают и обновляют карты всех масштабов и видов, выполняют фототрансформирование снимков и создают фотопланы. Во всех системах наведение марки на точку выполняется как с использованием коррелятора, так и оператором. В разных ЦФС маркой управляют различными средствами: "мышью", клавишами клавиатуры, джойстиком и даже штурвалами (двумя ручными и ножным на ЦФС ЦНИИГАиК).
3. ИСТОЧНИКИ, ВЛИЯЮЩИЕ НА ТОЧНОСТЬ ФОТОГРАММЕТРИЧЕСКОЙ ОБРАБОТКИ СНИМКОВ
3.1. Источники ошибок фотограмметрических измерений
Ошибки, действующие при фотограмметрических измерениях, можно объединить в пять групп в зависимости от их общего источника возникновения. Это ошибки: 1) снимка; 2) измерительного прибора; 3) опознавания точек; 4) методики обработки; 5) опорных точек.
1. Основными источниками ошибок снимка являются источники, вызывающие отклонения в положениях точек на нём от положений, соответствующих идеальной центральной проекции. Их действия рассмотрены в п. 3.2.
Нужно только отметить, что суммарное действие всех источников приводит к тому, что точность построения современных аэро- и космических фотоснимков равна примерно mXY = 15-20 мкм, а наземных фотоснимков 10-15 мкм.
2. У цифровых фотограмметрических систем собственно компьютер не вносит ошибок в измерения и вычисления. Ошибки появляются из-за нестрогости введённых в него программ. Следовательно, у этих систем инструментальные ошибки носят методический характер, о чем говорится в пункте 4. Аналитические фотограмметрические приборы в качестве измерительной системы имеют оптико-механическую конструкцию - стереокомпаратор, который накладывает на измерения свои ошибки. Однако эти ошибки небольшие и в целом приборы показывают высокую инструментальную точность, равную 1,5-3 мкм в плоскости снимков.
3. Ошибки, возникающие из-за неправильного опознавания точек и, соответственно, наведения измерительной марки на эти точки, могут существенно снижать точность фотограмметрических измерений. Опыт показывает, что для точных фотограмметрических работ необходимо перед аэросъёмкой выполнить маркирование точек на объекте съёмки. При этом наилучший эффект в опознавании точек будет достигнут, если точки будут покрашены краской, дающей максимальное отражение света в той зоне спектра, для которой аберрации у объектива фотокамеры сведены до минимума. В этом случае будет обеспечиваться наибольшая чёткость изображения замаркированной точки, и наведение на неё измерительной марки будет выполняться с точностью 5-10 мкм.
4. Методические ошибки возникают из-за нарушения строгой теории обработки снимков. Чем больше введено отступлений от строгой обработки, тем ниже точность конечного результата, но при этом сокращается время обработки. Если требуется высокоточный результат, то обработку проводят по строгой теории, хотя это и занимает больше времени.
5. Ошибки опорных точек учитываются при фотограмметрических измерениях в зависимости от того, с какой точностью координаты этих точек были определены. Если эта точность выше точности фотограмметрических измерений в 2-3 раза, то координаты опорных точек считают безошибочными. В противном случае окончательную точность фотограмметрических измерений определяют, суммируя ошибки опорных точек и фотограмметрических измерений. Например, при создании топографических карт в масштабах 1:10000 и мельче геодезические измерения координат опорных точек считаются безошибочными. В масштабах 1:500 и 1:1000 точность конечных результатов фотограмметрических измерений приближается к точности геодезических измерений и, следовательно, ошибки последних нужно учитывать.
В заключение нужно отметить, что невозможно определить влияние каждого источника ошибок в отдельности. Кроме того, характер действия каждого источника меняется в зависимости от многих факторов. Возможно также действие неизвестного источника. В связи с этим в фотограмметрии методику обработки снимков строят таким образом, что после исключения из измерений основной части систематических ошибок, вносимых источниками, действия которых достаточно хорошо описываются математическими зависимостями, оставшуюся часть ошибок исключают как единую ошибку с помощью специальной методики, называемой калибровкой снимков.
3.2. Источники, искажающие центральную проекцию на реальном снимке
Формулы преобразования координат между системами координат снимка и объекта выводят под условием, что изображение объекта на снимке получено в идеальной центральной проекции. Однако под действием различных факторов изображение на реальном снимке отклоняется от центральной проекции. Возникшие смещения точек приводят к тому, что вычисления по формулам связи между координатами точек снимков и объекта дают приближённые результаты. Исключение и учёт ошибок идет по двум направлениям:
1) получение снимков, максимально приближённых к центральной проекции, т.е. на этапе фотографирования стараются исключить или частично ослабить влияние известных источников ошибок;
2) применение такой методики фотограмметрической обработки, при которой будут максимально учтены ошибки снимков.
К источникам ошибок, вызывающим искажение центральной проекции на реальных снимках, относятся:
- дисторсия объектива фотокамеры,
- дисторсия выравнивающей стеклянной пластины фотокамеры,
- неплоскостность поверхности светочувствительного приёмника: фотоплёнки или матрицы (линейки) ПЗС,
- клинообразность светофильтра,
- атмосферная рефракция,
- деформация иллюминатора, - внутренняя рефракция, - деформация фотоматериала.
Использование цифровых фотокамер исключает или видоизменяет влияния перечисленных выше источников ошибок. В этих фотокамерах отсутствует стеклянная пластинка, к которой в фотокамерах прижимается фотоплёнка. Невыравнивание фотоплёнки в плоскость заменяется неплоскостностью поверхности матрицы или линейки ПЗС. Влияние светофильтра для обоих видов фотокамер возможно только в том случае, когда съёмка ведётся в определённых зонах спектра. Что касается деформации фотоматериала, нужно иметь в виду, что при переводе на сканере фотоснимков в цифровую форму на деформацию снимка накладываются инструментальные ошибки сканера.
Дисторсия объектива фотокамеры и деформация фотоматериала рассмотрены подробно в п. 3.3 и 3.4. Далее даётся краткая характеристика остальных источников ошибок.
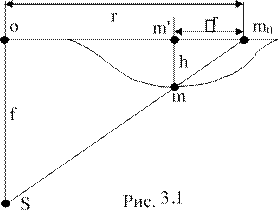 Влияние неплоскостности поверхности
светочувствительного приёмника: матрицы (линейки) ПЗС или фотоплёнки, на
положения точек на снимке показано на рис. 3.1. При плоской поверхности точка
местности изобразится в положении m0, а при отклонении от плоскости
на величину h - в точке m. При этом радиус-вектор r точки получится уменьшенным
на величину r.
Если принять, что величина r
должна быть меньше 20 мкм, то
Влияние неплоскостности поверхности
светочувствительного приёмника: матрицы (линейки) ПЗС или фотоплёнки, на
положения точек на снимке показано на рис. 3.1. При плоской поверхности точка
местности изобразится в положении m0, а при отклонении от плоскости
на величину h - в точке m. При этом радиус-вектор r точки получится уменьшенным
на величину r.
Если принять, что величина r
должна быть меньше 20 мкм, то
r
отклонение от плоскости h = f ![]() при r
при r
r = 70 мм не должно превышать 20 мкм для f = 70 мм и 60 мкм для f = 200 мм. Следовательно, требования к выравниванию в
плоскость поверхности светочувствительного материала выше у короткофокусных фотокамер, чем у длиннофокусных.
Светофильтр, устанавливаемый перед объективом фотокамеры, должен представлять собой стеклянную плоскопараллельную пластинку, однородную по всему объёму, без пузырей, свилей, царапин. Понятие клинообразность светофильтра введено в связи с тем, что при его изготовлении указанные выше требования выдерживаются с определёнными допусками. В результате, в первом приближении, светофильтр можно представить в виде оптического клина, который при прохождении через него оптических лучей вызывает их неодинаковое отклонение. При этом величина отклонения будет возрастать с увеличением угла падения луча на нижнюю поверхность светофильтра. Кроме того, максимальные отклонения хода лучей будут в нормальном сечении оптического клина, в котором находится угол клина. Следовательно, оптический клин будет деформировать связку оптических лучей и, соответственно, искажать центральную проекцию на снимке. Учёт влияния клинообразности светофильтра сопряжен с трудностями, т.к. нужно знать не только величину угла клина, но и угол разворота плоскости нормального сечения в системе координат снимка. Кроме того, светофильтр можно считать оптическим клином только в первом приближении. Поэтому при его изготовлении не допускают, чтобы величина угла между средними плоскостями верхней и нижней поверхностей превышала 10". При таком допуске ошибки в положениях точек на снимке не будут превышать 20 мкм.
 Смещения
точек на снимке под влиянием атмосферной рефракции возникают из-за того,
что оптический луч, идущий от точки M местности (рис. 3.2) до объектива
фотокамеры, проходит слои воздуха разной плотности, с разной температурой и
давлением и, следовательно, с разными коэффициентами преломления. В результате
оптический луч пройдет не по прямой МS, а по кривой, выгнутой во внешнюю
сторону. Угол
между прямой МS и касательной к кривой в точке S называют угловой фотограмметрической
рефракцией.
Смещения
точек на снимке под влиянием атмосферной рефракции возникают из-за того,
что оптический луч, идущий от точки M местности (рис. 3.2) до объектива
фотокамеры, проходит слои воздуха разной плотности, с разной температурой и
давлением и, следовательно, с разными коэффициентами преломления. В результате
оптический луч пройдет не по прямой МS, а по кривой, выгнутой во внешнюю
сторону. Угол
между прямой МS и касательной к кривой в точке S называют угловой фотограмметрической
рефракцией.
На снимке точка М изобразится не в точке m, а в точке m', т.е. под влиянием Рис. 3.2 атмосферной рефракции точки смещаются
от точки надира n вдоль радиусов-векторов r. Т.к. r = f tg, то dr = fsec2 d. Заменив dr на r, а d на , получим, что величина смещения точки под влиянием рефракции будет определяться формулой: f2 r2
r = - ![]() .
.
f
![]() На
основании этой формулы и с учётом, что r2 = x2 + y2
и r x y , r x y
На
основании этой формулы и с учётом, что r2 = x2 + y2
и r x y , r x y
можно получить формулы, по которым можно вводить поправки в измеренные на снимке координаты точек.
x2 y2 x2 y2 f f
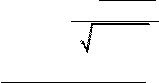
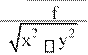 x = - x f , y = - y,
(3.1) x2 y2 = 0,000226 tg(Ha
H
) dg , На -
абсолютная высота фотографирования,
x = - x f , y = - y,
(3.1) x2 y2 = 0,000226 tg(Ha
H
) dg , На -
абсолютная высота фотографирования,
где
H
Нg - высота точки местности, d - изменение плотности атмосферы с высотой.
Формулы (3.1) выведены для горизонтальных аэроснимков, но их можно применять и для плановых аэроснимков. При крупномасштабной аэросъёмке влияние атмосферной рефракции невелико и её можно не учитывать.
Необходимо отметить следующее. Если аэросъёмка производится из герметизированной кабины, появляется источник искажений - деформация иллюминатора, перед которым устанавливают фотокамеру. Конструкции иллюминаторов бывают различной сложности. При съёмке с самолёта в качестве иллюминатора используют стеклянную плоскопараллельную пластину - стекло фотолюка, которое должно сохранять форму плоскопараллельной пластины с допусками, установленными для светофильтров. Иллюминаторы, устанавливаемые на космических носителях или глубоководных аппаратах, состоят из двух-четырех стекол. При космическом фотографировании иллюминатор, имеющий сложную конструкцию, находится в параллельном пучке оптических лучей, идущих от объектов, расположенных в бесконечности, поэтому за его идеальную форму целесообразно принять плоскопараллельную пластину, которая при таком ходе лучей не вызывает искажения фотоизображения. С внутренней и наружной сторон иллюминатора температуры и давления разные. Если иллюминатор состоит из нескольких стекол с воздушными камерами между ними, то на поверхностях каждого стекла будут собственные температура и давление. Разность температур по обеим сторонам стекол, а также различная теплопроводность металлической оправы и стекол приводит к неравномерности распределения температур внутри стекол. Под действием этих факторов стекла прогибаются в сторону наименьшего давления, а коэффициент преломления в разных точках стекол будет иметь разные значения. В результате меняется фокусное расстояние оптической системы иллюминатор-объектив фотокамеры и искажается ход оптических лучей. При подводной фотосъёмке возникают дополнительные требования к иллюминатору, что объясняется нестабильностью внешней среды с её переменами температуры, давления, коэффициента преломления хода оптических лучей.
Учёт влияния деформации иллюминатора путём расчёта поправок в измеренные координаты точек изображения сопряжен с трудностями и не даёт желаемых результатов из-за отсутствия конкретных данных на момент экспонирования снимка. Более целесообразной является разработка такой конструкции иллюминатора, которая практически не будет приводить к смещениям точек на снимке, полученном данной фотокамерой и в заданных условиях.
Фотосъёмка из герметизированной кабины через иллюминатор связана с еще одним источником искажений - внутренней рефракцией. В связи с тем, что иллюминатор является границей между двумя средами, имеющими различные оптические характеристики, ход оптических лучей имеет сложный характер. В кабине для нормальной работы аппаратуры создают условия, близкие к земным, а внешней средой могут быть либо вакуум (космическая фотосъёмка), либо вода (подводная фотосъёмка). Оптический луч, пройдя внешнюю среду и иллюминатор, попадает в газовую среду кабины, и направление его хода изменяется по сравнению с направлением, которое он имел во внешней среде. Угловую величину изменения направления называют внутренней фотограмметрической рефракцией. По аналогии с атмосферной рефракцией поправки в координаты точек фотоизображения рассчитывают по формулам (3.1), подставляя вместо значение угла внутренней рефракции. Необходимо отметить, что направления действия внутренней и атмосферной рефракций противоположны, и в результате частично компенсируют друг друга.
3.3. Дисторсия объектива фотокамеры
Дисторсия является одним из видов хроматической аберрации объектива и вызывает нарушение подобия между объектом и его изображением, т.е. объектив не обладает ортоскопией. Нарушение ортоскопичности объектива происходит из-за 1) невозможности достигнуть её уже на этапе расчёта оптической системы, 2) погрешностей при изготовлении отдельных оптических компонентов системы, 3) погрешностей при сборке оптической системы. При отсутствии погрешностей сборки вершинные точки сферических поверхностей линз, составляющих объектив, располагаются на его оптической оси. Такая оптическая система считается центрированной относительно её оптической оси, а возникающее в ней нарушение ортоскопичности называют дисторсией центрированной системы. Искажения изображения, возникающие из-за нарушения центрированности линз, называют нецентрированной дисторсией, при которой симметричность смещения точек не соблюдается.
При наличии центрированной дисторсии реальный объектив в отличие от идеальной оптической системы вызывает отклонение хода выходящего луча от направления, параллельного входящему лучу, т.е. имеют место неравенства углов ' и (рис. 3.3). Следовательно, точка объекта изображается на снимке Р не

![]() в точке К, а в точке
K'. Если смещения точек происходят от оптической оси (от точки о), т.е. ' , то дисторсию
считают положительной, а если к точке о ('
, то - отрицательной.
Величина смещения r
определяется длиной радиуса-вектора точки r0, но зависимость носит
нелинейный характер. В результате изображение не только изменяет свои размеры,
но и форму.
в точке К, а в точке
K'. Если смещения точек происходят от оптической оси (от точки о), т.е. ' , то дисторсию
считают положительной, а если к точке о ('
, то - отрицательной.
Величина смещения r
определяется длиной радиуса-вектора точки r0, но зависимость носит
нелинейный характер. В результате изображение не только изменяет свои размеры,
но и форму.
Предположим, что фотографируется квадрат (рис. 3.4). Его изображение при отсутствии дисторсии показано на рисунке пунктиром. Под влиянием центрированной дисторсии точки сторон квадрата будут смещаться по радиальным направлениям, проведённым из главной точки о. Смещения противоположных точек носят симметричный характер, поэтому центрированную дис-
Рис. 3.4 торсию называют радиальной, симмет-
ричной. В то же время смещения носят нелинейный характер. Например, смещения углов квадрата, отстоящих от точки о дальше, чем остальные точки сторон, будут максимальными, а смещения середин сторон - минимальными. В результате прямые линии будут преобразовываться в кривые второго порядка. При положительной дисторсии квадрат превратится в подушкообразную фигуру (как показано на рисунке утолщёнными кривыми), а при отрицательной дисторсии - в бочкообразную фигуру. Смещения r точек полученного изображения (например, точка К') относительно точек неискажённого изображения (точка К) называют абсолютной дисторсией. Её величину рассчитывают, используя полином, состоящий из членов с нечётными степенями:
r - ro = r = kor + k1r3 + k2r5 + ... . (3.2)
Первый член полинома выражает линейное увеличение изображения, ко-
торое можно компенсировать изменением фокусного расстояния: k0r
= ![]() f r. f
f r. f
Поэтому в фотограмметрии в искажённое дисторсией изображение вписывают неискажённое изображение, как бы полученное при фокусном расстоянии f ' = f + f (см. рис. 3.3) и называют его фокусным расстоянием фотокамеры. На рис. 3.4 вписанный неискажённый квадрат показан тонкими линиями. Точка К" этого квадрата соответствует точке К исходного квадрата. Отклонение rф точки К' от точки K" называют фотограмметрической дисторсией. Её величина, после исключения из полинома (3.2) члена первой степени, может быть вычислена путём использования полинома
rф = k1 r3 + k2 r5 + ... . (3.3)
Фокусное расстояние f ' и коэффициенты ki полинома (3.3) определяют при калибровке фотокамеры под условием rф2 = min.
В реальных объективах имеет место нецентрированная дисторсия, поэтому в фотограмметрии помимо радиальной дисторсии введено понятие тангенциальная дисторсия, под которой понимается смещение точек в направлении, перпендикулярном к радиальному. Их геометрическая сумма соответствует полной фотограмметрической дисторсии.
При фотограмметрической обработке снимков радиальная дисторсия вызывает искажения высот точек, например, модель плоской горизонтальной местности будет восприниматься в виде котловины или холма, а при соединении последовательных моделей будет происходить их прогиб. Под действием тангенциальной дисторсии появятся ошибки в передаче масштаба от модели к модели, произойдет их кручение и азимутальный разворот.
Учёт дисторсии сопряжен с трудностями не только потому, что распределение искажений по полю снимка имеет сложный вид, но и из-за того, что дисторсия объектива, как правило, определяется в лабораторных условиях на оптических скамьях-гониометрах, а в условиях реального полёта она может изменяться. Фотографические способы калибровки фотокамер по снимкам звездного неба и геодезического полигона фактически выявляют суммарные систематические ошибки снимков, а не дисторсию в чистом виде. Исключить влияние дисторсии можно двумя путями.
1. Изготовление фотокамер, у объективов которых практически отсутствует дисторсия. Достичь пока этого не удаётся, но у топографических фотокамер радиальная фотограмметрическая дисторсия не превышает 20 мкм, а тангенциальная - примерно в 3 раза меньше.
2. Путём введения поправок в измеренные координаты. С этой целью применяют таблицы, полиномы типа (3.3), избыточное число опорных точек.
Таблицы составляют на основании результатов определения дисторсии при калибровке фотокамеры. В таблице записывают поправки за дисторсию для координат точек с интервалом через 10 мм. Для точек, расположенных внутри этих интервалов, поправки определяются путём интерполяции между ближайшими табличными значениями.
При использовании полинома (3.3) радиус-вектор точки
заменяют её координатами согласно зависимостям: x
= x ![]() r , y = y
r , y = y ![]() r , r2 = x2
+ y2. В резуль-
r , r2 = x2
+ y2. В резуль-
r r
тате исправленные координаты точек рассчитывают по формулам:
xo = x [1- k1(x2+y2) - k2(x2+y2)2 -...], yo = y [1- k1(x2+y2) - k2(x2+y2)2 -...].
Значения коэффициентов ki берут из паспорта фотокамеры, куда их записывают после определения в ходе калибровки.
Учёт дисторсии с помощью избыточного числа опорных точек применяют при обработке снимков, если известно, что фотокамера имеет большую дисторсию, но нет её количественных значений. В этом случае избыточное количество опорных точек позволяет разделить стереопару или снимок на части. Например, добавив к четырем опорным точкам еще две, делят стереопару на две части: верхнюю и нижнюю, и ведут их обработку отдельно.
Нужно отметить, что плоскопараллельная стеклянная пластинка, устанавливаемая у некоторых фотокамер в плоскости прикладной рамки, вызывает радиальные сдвиги точек изображения, увеличивающиеся с увеличением угла падения оптического луча. Поэтому в расчёт объектива фотокамеры включают и плоскопараллельную пластинку, но полностью учесть её влияние не удаётся. Тем более что при прижиме фотоплёнки к этой пластинке прижимным столом, пластинка прогибается и вызывает дополнительные смещения точек. Фактически при калибровке фотокамеры определяют дисторсию системы объектив - выравнивающее стекло и учитывают её при измерениях.
3.4. Деформация изображения
Деформация изображения происходит из-за материала, на котором фиксируется изображение, и является одним из основных источников снижения точности фотограмметрических измерений. Если поставить условие, чтобы величины координат точек в пределах стереопары, составленной из снимков формата 23х23 или 18x18 см, не менялись больше, чем на 0,01 мм, то деформация не должна превышать 0,010 или 0,014, соответственно.
Из всех использовавшихся ранее фотоматериалов наибольшей деформа-
ции подвержена фотобумага, которая после фотолабораторной обработки и сушки сильно уменьшает свои размеры. Поэтому она использовалась только для создания либо первичных картографических документов (фотосхем, увеличенных снимков), либо фотопланов, служащих основами для изготовления графических планов и карт. Деформация фотоплёнки составляет 0,1-0,6. При этом 70-80 деформации приходится на подложку. Для длительного хранения снимки нужно переводить контактным путём с не разрезанного аэрофильма на стеклянные фотопластинки. Однако и они подвержены деформации из-за миграции фотоэмульсии, которая в среднем равна 2-3 мкм при максимальных значениях 10-12 мкм. Снимки на фотопластинках для последующих работ хранят в помещении с заданной температурой и влажностью.
В настоящее время в связи с развитием цифровой формы записи изображения снимки записывают на электронных носителях, которые сохраняют геометрию построения изображения в течение длительного времени. Для преобразования фотоснимков в цифровую форму используют фотограмметрический сканер, который обеспечивает, в целом, высокую точность сохранения геометрии исходного изображения. Однако и он вносит свои инструментальные ошибки в геометрию построения изображения.
Деформацию изображения подразделяют на систематическую и случайную. Систематическую деформацию делят на равномерную (одинаковую по всем направлениям) и неравномерную или разностную (неодинаковую в продольном и поперечном направлениях). Под случайной деформацией подразумевают искажение изображения, возникшее на небольшом участке.
Учёт систематической деформации при фотограмметрических измерениях производят разными способами:
1) введением поправок в измеренные на снимке координаты с помощью коэффициентов деформации или полиномов;
2) применением специальной методики измерения снимков; 3) использованием избыточного количества опорных точек.
Коэффициенты деформации изображения вдоль координатных осей x и y вычисляют по формулам
![]() lox и kдy = loy ,
lox и kдy = loy ,
kдx =
lx ly
где lox, loy - расстояния между противоположными координатными метками, взятые из паспорта фотокамеры, а lx, ly - измеренные значения этих же расстояний. Исправление измеренных координат выполняют по формулам
x = xи kдx и y = yи kдy.
Впечатывание в снимок сетки крестов позволяет, хотя и не полностью, учесть деформацию по площади снимка. Сетку крестов наносят на прижимное стекло, установленное в плоскости прикладной рамки фотокамеры. Координаты xoК, yoК крестов определяют путём компарирования сетки и заносят в паспорт фотокамеры. Измерив координаты xК, уК крестов на снимке, определяют их отклонения от компарированных значений. Расхождения x = xoК - xК и y = yoК - уК используют для вычисления коэффициентов полиномов типа
x a1 a x2 a y3 a xy4 a x5 2 a y6 2 a xy7 2 a x y8 2 . (3.4) y b1 b x2 b y3 a xy4 a x5 2 a y6 2 a xy7 2 a x y8 2
Для определения значений 16 коэффициентов нужно измерить 8 крестов. Т.к. на прижимном стекле кресты нанесены через 10 мм, то их число будет значительно больше. В этом случае предоставляется возможность, с одной стороны, для определения коэффициентов полиномов использовать метод наименьших квадратов, а с другой стороны повысить степень полиномов, если это нужно. После вычисления значений коэффициентов ai и bi их подставляют в полиномы и рассчитывают исправленные координаты xo = x + x и yo = y + y точек снимка. Использование полиномов позволяет уменьшить влияние деформации примерно в 1,5 раза.
У некоторых фотокамер, кроме четырех координатных меток, расположенных посредине каждой стороны, имеются еще четыре метки, расположенные в углах. Взаимное положение этих восьми меток в плоскости прикладной рамки определяют при калибровке фотокамеры и заносят в её паспорт. Наличие восьми меток позволяет использовать полиномы (3.4). Можно и при наличии четырех меток использовать полином, но в этом случае нужно снизить степень полинома, исключив последние четыре члена.
При наличии на снимке сетки крестов применяют методику измерения координат точек от ближайшего креста, считая, что деформация между ближайшими крестами, расстояния между которыми равно 1 см, практически мала. Координата точки складывается из компарированных значений координат xoК и yoК креста и приращений координат точки относительно этого креста, которые вычисляют по разности измеренных координат х, у точки и xК, yК креста, т.е. xо = xoК + (x - xК), yо = yoК + (y - yК). Абсолютные значения (x - xК), (y - yК) не должны превышать половины расстояния между соседними крестами. Использование такой методики измерения координат точек снимков позволяет снизить влияние деформации примерно в 2-3 раза.
Избыточное количество опорных точек позволяет учесть деформацию путём деления снимка (стереопары) на части, в пределах которых величины деформации изменяются незначительно. Например, шесть опорных точек позволяют разделить снимок (стереопару) на две части: верхнюю и нижнюю, а девять точек - на четыре части: две вверху и две внизу. Каждая часть обрабатывается отдельно.
Необходимо отметить, что все перечисленные способы позволяют учесть систематическую деформацию только в общих чертах, но не в каждой точке снимка.
3.5. Смещения точек на снимке, вызванные его наклоном
На наклонном снимке точки смещены от положений, которые они должны занимать на горизонтальном снимке, полученном той же фотокамерой из того же центра проекции. Получим формулу, по которой можно рассчитать эти смещения, и в результате определить, можно ли по этому снимку выполнять измерения, не выполняя фотограмметрических преобразований. Воспользуемся тем, что у обоих снимков есть общие точки, расположенные на линии неискажённых масштабов hchc (см. рис. В.1 и рис. 3.5, а). Перпендикулярно этой ли-
 o
o
нии проходит главная вертикаль vv, которая является линией пересечения снимка главной вертикальной плоскостью V, проведённой через главный оптический луч So и отвесную линию Sn (рис. 3.5, б выполнен в этой плоскости). На рис. 3.5, а наклонный Р и горизонтальный Ро снимки показаны совмещёнными после поворота вокруг линии hchc. На пересечении линии hchc с главной вертикалью vv находится точка нулевых искажений c. Свойством этой точки является то, что углы между направлениями, проведёнными через неё на наклонном и горизонтальном снимках одинаковы. Поэтому на рисунке направления на точку m на наклонном снимке и соответствующую ей точку m0 на горизонтальном снимке совпали.
Учитывая сказанное, используем полярную систему координат, которую расположим на обоих снимках следующим образом. Линию неискажённых масштабов hchc возьмём в качестве полярной оси, а точку c - в качестве полюса. Выбор этой системы координат объясняется еще и тем, что она будет менять свое положение в плоскости снимка в зависимости от угловых элементов внешнего ориентирования. В результате можно не принимать во внимание наличие угла разворота снимка, а вместо поперечного и продольного углов наклона использовать суммарный угол o наклона снимка.
Положения точек m и m0 на снимках заданы радиус-векторами r = cm и r0 = cm0 и углом поворота этих радиус-векторов против часовой стрелки от полярной оси. Спроектируем точки m и m0 на главную вертикаль vv и получим точки mv и m0v. Радиус-векторы rv и r0v этих точек будут равны:
rv = cmv = r sin , r0v = cm0v = r0 sin. (3.6)
Из подобия треугольников Scm0v и Skmv (рис. 3.5, б) можно записать:
![]() rov
f rv .
(3.7) f r
sinv o
rov
f rv .
(3.7) f r
sinv o
Подставим радиус-векторы (3.6) в (3.7) и после деления левой и правой частей равенства на sin получим формулу связи координат точек наклонного и горизонтального снимков в полярной системе координат:
ro
![]() f r .
(3.8) f rsinsino
f r .
(3.8) f rsinsino
На наклонном снимке смещения точек происходят вдоль их радиусвекторов на величины r = r - r0. В эту формулу подставим формулу (3.8) и после преобразований получим формулу смещения точки на снимке, вызванного его наклоном.
![]() r = - sino .
(3.9)
r = - sino .
(3.9)
f rsinsino
0
Т.к. у плановых аэроснимков угол наклона не превышает 3 , в знаменателе формулы (3.9) можно опустить член rsinsin по его малости в сравнении с фокусным расстоянием f. В результате получим приближённую формулу
![]() r = - r2 sin sin o
. (3.10) f
r = - r2 sin sin o
. (3.10) f
На основании формулы (3.10) можно сделать вывод, что:
1) r = 0 при = 0 или 1800, т.е. точки, расположенные на линии неискажённых масштабов, не смещаются под влиянием угла наклона аэроснимка;
2) r = max при = 900 или 2700, что соответствует линии главной вертикали vv, а при r = max на точках, расположенных на главной вертикали на краю снимка.
Из формулы (3.10) также видно, что величина смещения r находится в обратной пропорциональной зависимости от величины фокусного расстояния фотокамеры и в прямой квадратичной зависимости от радиус-вектора точки (формата кадра). Поэтому, если нужно получить снимки с минимальными смещениями, вызванными его углом наклона, то аэросъёмку следует выполнять длиннофокусными фотокамерами с небольшим форматом кадра.
Кроме угла наклона смещения точек на снимке вызывает рельеф местности. По законам построения изображения в центральной перспективной проекции точка М местности (рис. 3.6) изобразится на снимке Р в точке m, отстоящей от точки надира n на расстоянии r. При создании топографических карт точки местности должны быть спроектированы отвесными линиями на поверхность референц-эллипсоида. На снимках, по которым создаются крупномасштабные топографические карты, изображаются сравнительно небольшие по площади участки местности, в пределах которых поверхность референцэллипсоида можно принять за плоскость, а проекцию можно считать ортогональной. Таким образом, точка местности М будет проектироваться на горизонтальную плоскость Е, представляющую участок поверхности референцэллипсоида, в точку Мо.
![]() Если изображение, полученное на снимке Р,
спроектировать по законам центральной проекции на плоскость Е, то
точка m спроектируется в точку М', а не в точку Mо.
Чтобы точка m спроек
тировалась в точку Мо, необходимо сместить её на снимке
в точку mо. Ве личину смещения - отрезок mmо = rh
- называют смещением точки, вызван ным рельефом местности. Эти
сме щения представляют собой несовпа дения изображений
местности на кар те и полученных путём проектирова ния со снимка
из-за их разных проек-
Если изображение, полученное на снимке Р,
спроектировать по законам центральной проекции на плоскость Е, то
точка m спроектируется в точку М', а не в точку Mо.
Чтобы точка m спроек
тировалась в точку Мо, необходимо сместить её на снимке
в точку mо. Ве личину смещения - отрезок mmо = rh
- называют смещением точки, вызван ным рельефом местности. Эти
сме щения представляют собой несовпа дения изображений
местности на кар те и полученных путём проектирова ния со снимка
из-за их разных проек-
ций. При фотограмметрической обра-
ботке снимков это нужно учитывать.
Из подобия треугольников SNMo и Snmo, а также SN'M и Snm запишем:
![]() R (r r
)Hh r(H
h) . После преобразований получим формулу смещений f f точек
на горизонтальном снимке, вызванных рельефом местности. rh
R (r r
)Hh r(H
h) . После преобразований получим формулу смещений f f точек
на горизонтальном снимке, вызванных рельефом местности. rh
rh =
![]() .
(3.11)
.
(3.11)
H
Из анализа формулы (3.11) можно сделать вывод, что rh = 0 при:
1) r = 0, т.е. в точке надира n смещение, вызванное рельефом местности, отсутствует. Это объясняется тем, что точка надира является точкой пересечения снимка отвесной линией, т.е. она единственная точка снимка, которая будет соответствовать ортогональной проекции;
2) h = 0, т.е. изображение плоской горизонтальной местности преобразуется из центральной проекции в ортогональную проекцию без ошибок.
Увеличение высоты фотографирования Н приводит к уменьшению величин смещений точек на снимке. Т.к. Н = fm, можно сделать вывод, что на длиннофокусных снимках смещения точек будут меньше, чем на короткофокусных. В то же время увеличение рельефа и радиус-вектора точек приводит к увеличению их смещений, и наибольшие их величины будут на краю снимка. Следовательно, если необходимо получить снимки с минимальными смещениями, вызванными рельефом местности, то аэросъёмку следует выполнить с максимально возможной высоты и длиннофокусной фотокамерой с небольшим форматом кадра.
3.7. Сдвиг изображения в плоскости прикладной рамки фотокамеры
Сдвиг изображения в плоскости прикладной рамки фотокамеры возникает из-за её линейных и угловых перемещений во время экспонирования снимка. Основной источник сдвига изображения - линейное перемещение фотокамеры в направлении полёта носителя. В момент начала открытия затвора точка М
![]() (рис. 3.7) объекта
изображается на снимке Р в точке m. За время выдержки t центр проекции S
перемещается на расстояние SS' = Vt, где V - скорость дви P m P m m' жения
фотокамеры. В это же время точка М продолжает изображаться на снимке Р, и в
момент
(рис. 3.7) объекта
изображается на снимке Р в точке m. За время выдержки t центр проекции S
перемещается на расстояние SS' = Vt, где V - скорость дви P m P m m' жения
фотокамеры. В это же время точка М продолжает изображаться на снимке Р, и в
момент
закрытия затвора она будет проектироваться в точку m'. В результате точка М изобразится на снимке в виде отрезка mm' = . Этот отрезок и является сдвигом изображения в плоскости прикладной рамки. Его длину можно рассчитать по формуле, полученной из подобия треугольников MSS' и S'mm'.
f
= Vt ![]() ,
(3.12)
,
(3.12)
H
т.е. длина линии mm' равна величине смещения центра проекции SS' в масштабе съёмки.
Из формулы видно, что величина стремится к минимуму, если скорость V, выдержка t и фокусное расстояние f тоже стремятся к минимуму, а высота фотографирования Н стремится к максимуму.
Однако отрезок mm' полностью не виден на снимке, т.к. приёмник светового потока чувствителен к его определённой силе. Из-за этого в начале открытия и в конце закрытия затвора, когда световой поток недостаточно силён, начало и конец линии mm' не будут видны. Видимую часть линии называют смазом изображения.
Если сдвиг изображения, рассчитанный по формуле (3.12), превышает 0,05 мм, то используют фотокамеру с компенсатором этого сдвига, например, путём смещения прикладной рамки вместе с приёмником светового потока в направлении сдвига изображения.
Необходимо отметить, что сдвиг изображения в плоскости прикладной рамки не вызывает искажения центральной проекции, но приводит к нерезкости изображения и, следовательно, к снижению точности наведения измерительной марки, а также к ухудшению дешифрируемости изображения.
3.8. Влияние сферичности Земли на фотограмметрические измерения
При создании топографических карт точки земной поверхности проектируют отвесными линиями на поверхность референц-эллипсоида, выбранного в качестве математической фигуры Земли. При фотограмметрической обработке снимков модель земной поверхности измеряется в прямоугольной системе координат, и для получения плана этой поверхности точки модели проектируют на горизонтальную координатную плоскость параллельным пучком лучей, ортогональным к этой плоскости. Последнюю можно принять за часть поверхности референц-эллипсоида только при условии, что аппроксимация сферической поверхности плоскостью приводит к ошибкам, не превышающим допустимые значения для топографической карты данного масштаба.
Точку сферической поверхности М (рис. 3.8) спроектируем ортогонально
![]() на плоскость Е
(координатную плоскость XY) и получим точку Мо. Точки М
и Мо по законам центрального проектирования перенесем на
снимок Р и получим точки m и mo. Расстояние mmo
= rR
называют смещением точки на снимке, вызванным сферичностью Земли. Смещение
происходит в сторону точки надира n по направлениям, проведённым через
эту точку. Это смещение происходит в противоположном направлении, чем из-за
атмосферной рефракции. Следовательно, происходит частичная компенсация влияний
этих двух источников ошибок на положения точек на снимке.
на плоскость Е
(координатную плоскость XY) и получим точку Мо. Точки М
и Мо по законам центрального проектирования перенесем на
снимок Р и получим точки m и mo. Расстояние mmo
= rR
называют смещением точки на снимке, вызванным сферичностью Земли. Смещение
происходит в сторону точки надира n по направлениям, проведённым через
эту точку. Это смещение происходит в противоположном направлении, чем из-за
атмосферной рефракции. Следовательно, происходит частичная компенсация влияний
этих двух источников ошибок на положения точек на снимке.
Найдем формулу расчёта высоты Н фотографирования в зависимости от заданной величины rR. В прямоугольном треугольнике NMN' перпендикуляр L, опущенный из вершины прямого угла на гипотенузу, делит её на от-
резки, произведение которых равно квадрату длины перпендикуляра:
L2 h(2R h). (3.13)
Из подобия треугольников monS и MoNS найдем
![]() L H(r rR ) ,
(3.14) f
L H(r rR ) ,
(3.14) f
а из подобия треугольников mnS и MКS
L
![]() (H
h)r .
(3.15) f
(H
h)r .
(3.15) f
Приравняв правые части формул (3.14) и (3.15), после преобразований получим
![]() h H rR .
(3.16) r
h H rR .
(3.16) r
![]() Подставим формулы (3.15) и
(3.16) в (3.13) и после преобразований получим: H = 2Rf r r2 R . r + f4 2rR2
Подставим формулы (3.15) и
(3.16) в (3.13) и после преобразований получим: H = 2Rf r r2 R . r + f4 2rR2
В знаменателе член f2rR2 можно опустить по малости по сравнению с ве-
4 личиной r . Например, при r = 100 мм, f = 1000 мм и rR = 0,01 мм величина r4 = 100 000 000 мм4, а величина f2rR2 = 100 мм4. После преобразования получим приближённую формулу, по которой удобно рассчитать максимально допустимую высоту фотографирования при заданной величине смещения точки на снимке, вызванного сферичностью Земли.
2Rf2
![]() H = 3 rR
. (3.17) r
H = 3 rR
. (3.17) r
Из формулы (3.17) можно сделать вывод, что увеличению высоты фотографирования способствуют больший диаметр 2R планеты, увеличение фокусного расстояния f фотокамеры (квадратическая зависимость) и уменьшение формата кадра r (кубическая зависимость).
В таблице 3.1 приведены значения высот фотографирования, ниже которых в пределах рабочей площади снимков влияние сферичности Земли (R = 6371 км) при rR 0,01 мм можно не учитывать. В числителе указаны высоты фотографирования для формата 18х18 см (радиус-вектор угла рабочей площади снимка r = 70 мм), а в знаменателе - для формата 23х23 см (r = 90 мм).
Таблица 3.1
|
f, мм |
70 |
100 |
140 |
200 |
350 |
500 |
1000 |
|
Н, км |
|
|
|
|
|
|
|
Топографическая аэросъёмка Земли производится с высот, не превышающих 5 км, и из таблицы можно сделать вывод, что для формата 18х18 см влияние сферичности Земли можно не учитывать для f 100 мм, а для формата 23х23 см - для f 140 мм.
Необходимо отметить, что сферичность Земли не искажает центральной проекции земной поверхности на плоскости снимка и понятие "смещение точки, вызванное сферичностью Земли" появляется только тогда, когда проектирование точек земной поверхности производится не на поверхность референцэллипсоида отвесными линиями, а на плоскость в ортогональной проекции. Следовательно, данный источник ошибок носит методический характер. Особенно сильно влияние сферичности Земли и других планет проявляется при фотограмметрической обработке космических снимков, т.к. у них высоты фотографирования на много превышают высоты, указанные в таблице 3.1. Особенности фотограмметрической обработки космических снимков описаны в 11.5.
4. СИСТЕМЫ КООРДИНАТ И ЭЛЕМЕНТЫ ОРИЕНТИРОВАНИЯ СНИМКОВ
4.1. Системы координат, применяемые в фотограмметрии
При фотограмметрической обработке снимков используют следующие прямоугольные системы координат:
- система координат измерительного прибора;
- система координат снимка с началом в его плоскости;
- система координат снимка с началом в его центре проекции; - система координат сфотографированного объекта; - система координат модели объекта.
Т.к. фотограмметрическая обработка снимков заключается в преобразовании координат из одной системы координат в другую, необходимо обратить особое внимание на данный раздел. Запомнив, как задаётся положение каждой из указанных систем координат, и каково их взаимное положение, легче понять описываемые в дальнейшем процессы перехода из одной системы координат в другую. В большинстве случаев используются приведённые в справочниках по математике формулы преобразования пространственных координат. В фотограмметрии в эти формулы добавляют масштабный коэффициент, т.к. часто системы координат находятся в разных масштабах. Далее рассматриваются особенности каждой указанной выше системы координат.
Система координат измерительного прибора в настоящее время имеет место только в АФП, где измерительным блоком является стереокомпаратор, у которого система координат задаётся взаимно перпендикулярными направляющими. По ним перемещаются каретки, несущие левый и правый снимкодержатели. Эта система координат - плоская и правая. Её обозначим c'x'y'z', и у каждой точки снимка координата z' = 0.
Система координат снимка с началом в его плоскости имеет особенности, связанные с тем, в какой форме был получен исходный снимок: цифровой или аналоговой (на фотоплёнке). В цифровой фотокамере снимок сразу получается в цифровой форме. Аналоговые фотоснимки для обработки на компьютере нужно переводить в цифровую форму на фотограмметрическом сканере.
Система координат фотограмметрического сканера задаётся направляющей и перемещающейся по ней светочувствительной линейкой ПЗС, расположенной под углом 900 к направляющей. У цифровой фотокамеры система координат задаётся матрицей ПЗС. Цифровое изображение представляет собой матрицу, состоящую из квадратов-пикселов, содержащих информацию об оптической плотности и цвете (три основных цвета: красный, зелёный, синий) данного участка изображения. Изменение оптической плотности от белого до чёрного задаётся цифрами от 0 до 256. Столько же ступеней используется для трёх основных цветов.
4.2. Система координат цифрового снимка с началом в его плоскости
Для определения положения точек на цифровом снимке используют сис-
![]() тему
пиксельных координат c'xjyiz' (рис. 4.1, а) и систему
физических коорy' динат
c'x'y'z'. У этих систем коорди-
тему
пиксельных координат c'xjyiz' (рис. 4.1, а) и систему
физических коорy' динат
c'x'y'z'. У этих систем коорди-
нат начало и оси совпадают, но систе-
z' ма пиксельных координат - левая, а
система физических координат - правая. Т.к. измеряется плоское изобра-
i жение, у всех точек снимка координата
z' = 0.
Начало c' обоих систем координат расположено в левом верхнем углу. Положения пикселов задаются но-
yi мером столбца j и номером строки i.
Увеличение номеров для столбцов -
вправо, а для строк - вниз. Первый пиксел является нулевым, т.е. у него j = 0 и i = 0. Для закрашенного пиксела j = 5 и i = 3.
Пиксельные координаты центров пикселов рассчитывают по формулам xj = j + 0,5 и yi = i + 0,5. Следовательно, для нулевого пиксела пиксельные координаты xj = 0,5 и yi = 0,5, а для закрашенного пиксела - xj = 5,5 и yi = 3,5.
Для перехода от пиксельных координат к физическим координатам, которые участвуют в дальнейших преобразованиях, используют формулы: x' = xj и y' = -(yi),
где - физический размер стороны пиксела, заданный при сканировании снимка (см. п. 1.6) или при изготовлении матрицы цифровой фотокамеры. У координаты y' ставится знак минус для перехода к правой системе координат. Например, при = 20 мкм физические координаты закрашенного пиксела будут x' = 5,520 мкм = 110 мкм и y' = -(3,520) мкм = -70 мкм.
На
компьютере каждый пиксел исходной матрицы можно заменить подматрицей nn из
пикселов меньшего размера (рис. 4.1, б). Это позволяет увеличить изображение на
экране монитора в n раз и выполнить измерения с точностью 1/n исходного
размера пиксела. На рисунке показана подматрица размером 4х4 закрашенного
пиксела исходной матрицы, т.е. изображение увеличено в 4 раза. Подматрица имеет
свою систему счёта координат: j' - номер столбца и i' - номер
строки, и координаты центров пикселов рассчитывают по формулам: xj j ![]() j'
0,5 , yi i
j'
0,5 , yi i ![]() i' 0,5 . n n
i' 0,5 . n n
На исходной матрице закрашенный пиксел имеет
нумерацию j = 5, i = 3. На подматрице закрашенный пиксел имеет
нумерацию j' = 2, i' = 1. Следовательно, пиксельные координаты
центра закрашенного пиксела подматрицы будут xj = 5+![]() = 5,625, yi = 3+
= 5,625, yi = 3+![]() = 3,375, а
физические координаты при
= 3,375, а
физические координаты при
= 20 мкм будут x' = 112,5 мкм, y' = -67,5 мкм.
Таким образом, в результате измерения цифрового снимка каждая точка в системе координат c'x'y'z' получает координаты x', y', z' = 0. При калибровке цифровой камеры, чтобы исключить отрицательные координаты, начало c' системы физических координат переносят в левый нижний пиксел.
4.3. Система координат аналогового снимка с началом в его плоскости
Система координат аналогового снимка o'xyz (рис. 4.2) закрепляется

на нём четырьмя координатными метками, которые могут располагаться посредине каждой стороны снимка (рис. 4.2, а) или в его углах (рис. 4.2, б). Координатные метки имеют вид креста, окружности или крестообразно расположенных штрихов с точкой посредине.
В первом варианте ось х проходит через координатные метки 1 и 2. Началом системы координат служит точка о' пересечения оси х линией, соединяющей метки 3 и 4. Ось у проходит через точку о' перпендикулярно к оси х, а ось z - через точку о' перпендикулярно к плоскости xy. Положительное направление оси х задают от метки 1 к метке 2, оси у - от метки 4 к метке 3, а оси z - вверх от плоскости xy. Необходимо отметить, что в разных программах обработки снимков нумерация меток может быть задана иная, но положительные направления координатных осей относительно снимка будут такими же.
Во втором варианте началом системы координат о' служит точка пересечения линий, соединяющих метки 1, 3 и 2, 4. Ось x проходит через точку о' параллельно линии, соединяющей координатные метки 1 и 2. Оси у и z проходят так же, как и в первом варианте.
В результате измерения снимка положения его точек в системе координат o'xyz будут определяться координатами x, y, z = 0.
4.4. Система координат снимка с началом в его центре проекции. Элементы внутреннего ориентирования снимка
Измерив координаты точек снимка в цифровой системе координат c'x'y'z' или в заданной координатными метками системе координат o'xyz (рис. 4.3), их преобразуют во вторую систему координат Sxyz снимка, начало которой находится в его центре проекции S. Ось z этой системы координат совмещена с главным оптическим лучом So. Оси x и y системы координат Sxуz параллельны соответствующим осям системы координат о'хуz или c'x'y'z' и имеют такие же положительные направления. Чтобы не загромождать рис. 4.3, на нём показана только система координат о'хуz, т.к. переход к системе координат

Sxуz для обоих систем одинаков и заключается только в переносе начала отсчёта координат из точки o' или точки с' в точку S. Для этого нужно знать координаты xS, yS, zS центра проекции S в системе координат о'хуz или c'x'y'z'.
Ими являются координаты xо, уо главной точки о снимка и фокусное расстояние f фотокамеры, т.е. xS = xо, yS = уо, zS = f.
Вычитая координаты центра проекции из координат точек снимка, измеренных в системе координат о'хуz (c'x'y'z'), получают координаты точек в системе координат Sхуz: x-xS = x-xо, y-уS = y-уо, z-zS = -f, т.е. точка m снимка имеет координаты: x-xо, y-уо, z = -f.
Величины xо, уо, f называют элементами внутреннего ориентирования снимка. Определив с их помощью положение центра проекции относительно снимка, можно провести проектирующие лучи через центр проекции и точки снимка, например, луч SmM. В результате будет восстановлена связка проектирующих лучей, существовавшая в момент экспонирования изображения.
При изготовлении измерительных фотокамер главную точку о и точку о' старались совместить. Однако достигнуть такого положения практически не удаётся, и обычно величины координат xо и уо не превышали 20 мкм. Такое условие нужно было соблюдать при обработке снимков на оптико-механических приборах. При обработке на компьютере это не имеет значения, и в 4.2 было указано, что начало системы физических координат c'x'y'z' находится в левом верхнем или нижнем пикселе. Следовательно, координаты xо и уо главной точки при калибровке цифровой фотокамеры будут получаться равными половине соответствующей стороны кадра.
4.5. Продольный и поперечный параллаксы
При измерении стереопары кроме координат точек используют разности этих координат на обоих снимках, называемые параллаксами (рис. 4.4). При стереосъёмке точки объекта изображаются в разных частях левого и правого снимков. Например, на левом снимке точка объекта изобразилась в точке m. В системе координат o'ЛxЛyЛ это-
![]() го снимка она будет
иметь координаты xЛ, yЛ. На правом снимке
та же точка объекта изобразилась в точке m', и в П системе координат o'ПxПyП
она имеет координаты xП, yП.
го снимка она будет
иметь координаты xЛ, yЛ. На правом снимке
та же точка объекта изобразилась в точке m', и в П системе координат o'ПxПyП
она имеет координаты xП, yП.
По координатам xЛ, yЛ нанесем на правом снимке по-
Рис. 4.4 ложение точки m. Смещения
точки m' относительно точки m вдоль координатных осей х и у являются, соответственно, продольным (буква р) и поперечным (буква q) параллаксами. Их величины рассчитывают по формулам: p = xЛ - xП, q = yЛ - yП. От чего зависят величины этих параллаксов рассмотрено в п. 5.6.
4.6. Система координат объекта. Элементы внешнего ориентирования снимка и пары снимков
В результате фотограмметрической обработки снимков координаты точек объекта должны быть получены в его системе координат OXYZ (рис. 4.5), по ложение которой задаётся конструкцией объекта. Если положение этой системы координат неизвестно, то координаты точек объекта определяют в фотограмметриче-
![]() X ской
системе координат SХYZ, ориентацию которой задают:
X ской
системе координат SХYZ, ориентацию которой задают:
1) с учётом конструкции объекта,
2) с учётом ориентации системы координат фотограмметрической модели объекта или устанавливают
3) параллельно системе координат Sxyz снимка.
При наличии у объекта сис-
темы координат OXYZ фотограмметрическую систему координат SXYZ используют на этапе обработки в качестве промежуточной.
В нашей стране при создании топографических карт применяют геодезическую систему координат ОГXГYГZГ, связанную с проекцией ГауссаКрюгера. В этой системе координат задают координаты опорных точек и, соответственно, получают конечные результаты. Однако геодезическая система координат - левая. В связи с этим перед началом фотограмметрической обработки снимков координаты опорных точек преобразуют в правую систему координат, а по окончании обработки снимков полученные координаты измеренных точек местности преобразуют в левую систему координат.
При фотограмметрической обработке снимков, охватывающих большие площади планеты, нельзя использовать геодезическую систему координат, т.к. она не является единой для всей поверхности планеты. Такой системой координат является планетоцентрическая OЦXЦYЦZЦ, и она в фотограмметрии используется в качестве системы координат объекта, что рассматривается в главе, посвящённой обработке космических снимков (см. 11.5).
Чтобы выполнить преобразование координат из системы координат снимка в систему координат объекта, нужно знать взаимную ориентацию этих систем. Она определяется элементами внешнего ориентирования снимка, которые фиксируют систему координат Sxyz снимка в таком положении относительно системы координат ОХУZ объекта, которое она имела в момент съёмки. Элементов внешнего ориентирования - шесть: три линейных и три угловых.
Линейными элементами внешнего ориентирования снимка являются координаты центра проекции XS, YS, ZS (см. рис. 4.5), определяющие его положение в системе координат объекта и характеризующие несовпадение начал систем координат Sxyz и ОХУZ.
Угловыми элементами внешнего ориентирования снимка являются углы , , , определяющие величину отклонения системы координат Sxyz от положения, при котором она была параллельна системе координат OXYZ.
У правой системы координат первичной считается ось Х. Вокруг этой оси выполняется первый поворот на угол . Второй поворот выполняется вокруг оси Y на угол , а третий поворот - вокруг оси Z на угол . Положительным направлением поворота правой системы координат принят поворот против часовой стрелки, если смотреть со стороны положительного направления координатной оси, вокруг которой выполняется поворот. Следовательно, если к моменту экспонирования снимка его система координат выполнила три поворота против хода часовой стрелки от положения, при котором она была параллельна системе координат объекта, то углы , , считаются положительными.
Углы и (см. рис. 4.5) определяют величину отклонения главного оптического луча So, с которым совмещена ось z системы координат снимка, от положения, при котором он был параллелен оси Z системы координат объекта.
Угол называют поперечным углом наклона снимка. Он лежит в вертикальной плоскости V, проведённой через отвесную линию SN параллельно координатной плоскости YZ.
Угол называют продольным углом наклона снимка. Он лежит в плоскости V, проведённой через главный оптический луч Sо перпендикулярно к координатной плоскости YZ.
Угол называют углом разворота снимка в своей плоскости вокруг главного оптического луча So. Угол лежит в плоскости снимка и определяет отклонение оси х системы координат Sxyz от линии oX пересечения снимка плоскостью V. Эта линия параллельна координатной плоскости ХZ.
Угол о определяет наклон главного оптического луча Sо в главной вертикальной плоскости V, и его называют углом наклона снимка. Углы и являются проекциями угла о на плоскости V и V.
![]() Положение
пары снимков в координатной системе OXYZ (рис. 4.6) объекта определяется
12 элементами внешнего ориентирования: шестью элементами внешнего
ориентирования левого снимка и шестью элементами внешнего ориентирования
правого снимка:
Положение
пары снимков в координатной системе OXYZ (рис. 4.6) объекта определяется
12 элементами внешнего ориентирования: шестью элементами внешнего
ориентирования левого снимка и шестью элементами внешнего ориентирования
правого снимка:
XSЛ, YSЛ, ZSЛ, Л, Л, Л, ХSП, YSП, ZSП, П, П, П. (4.1)
Координаты правого центра проекции можно вычислить через координаты левого центра проекции и проекции базиса фотографирования на координатные оси: ХSп = XSл + BX, YSп = YSл + BY, ZSп = ZSл + BZ. Вычисление базисных составляющих производится по формулам
BX cos cos
BY BA B cos sin . (4.2)
BZ sin
Последовательность поворотов на углы и , а также их положительные значения задаются положительными значениями проекций базиса BY и BZ, соответственно. Считается, что правый центр проекции вначале смещается параллельно оси X на величину BX, затем параллельно оси Y на величину BY и потом параллельно оси Z на величину BZ. Следовательно, первым будет угол , определяющий разворот базиса вокруг оси Z от положения, при котором он был параллелен координатной плоскости XZ. Положительное значение угла отсчитывается против хода часовой стрелки, если смотреть с положительного конца оси Z. Вторым будет угол , определяющий наклон базиса к координатной плоскости XY. Его положительное значение отсчитывается по ходу часовой стрелки, если смотреть с положительного конца оси Y.
На основе (4.2) значения углов и можно вычислить по формулам
BZ = arctg BZ , = arctg BY . (4.3) =arcsin
![]() B BX2 BY2 BX
B BX2 BY2 BX
С учётом элементов ориентирования базиса 12 элементов внешнего ориентирования (4.1) пары снимков в координатной системе ОХУZ можно записать в виде:
XSЛ, YSЛ, ZSЛ, Л, Л, Л, B, , , П, П, П. (4.4)
В системе координат SЛXУZ, параллельной координатной системе ОХУZ, начало отсчёта координат расположено в центре проекции левого снимка, поэтому XSл = YSл = ZSл = 0. В результате для пары снимков в координатной системе SЛXУZ из 12 элементов внешнего ориентирования (4.4) не равными нулю будут девять:
Л, Л, Л, B, , , П, П, П. (4.5)
4.7. Системы координат модели объекта. Элементы взаимного ориентирования пары снимков
При построении модели объекта используется система координат SЛXМYМZМ, у которой начало отсчёта координат расположено в центре проекции левого снимка. По аналогии с системой координат SЛXУZ объекта в системе координат SЛXМYМZМ пара снимков имеет 12 элементов ориентирования, из которых XМSл = YМSл = ZМSл = 0. Остальные 9 элементов аналогичны элементам внешнего ориентирования (4.5). Чтобы отличать их от элементов внешнего ориентирования, введём индекс "штрих", а базис обозначим буквой b, т.к. его длина задаётся в масштабе модели, и он называется базисом проектирования.
Л', Л', Л', b, ', ', П', П', П'. (4.6)
Эти элементы ориентирования определяют расположение базиса проектирования и двух связок проектирующих лучей левого и правого снимков в системе координат SЛXМYМZМ. Однако для облегчения построения модели, расположение системы координат SЛXМYМZМ задают так, чтобы часть элементов ориентирования (4.6) стали равными нулю. С этой целью используют две системы координат: базисную и левого снимка.
1. Базисная система координат SЛXМYМZМ (рис. 4.7, а) названа так по-
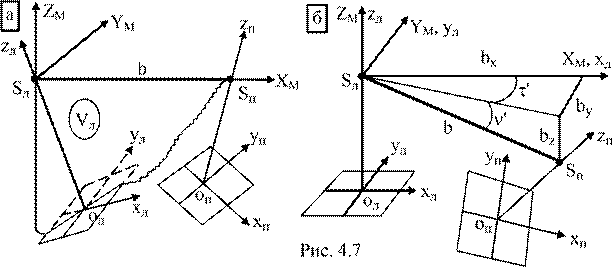
тому, что ось ХМ совмещена с базисом проектирования SЛSП, а ось ZМ расположена в главной базисной плоскости VЛ левого снимка, проведённой через базис b и главный оптический луч SЛoЛ. Ось YМ дополняет систему до правой.
2. Система координат левого снимка SЛXМYМZМ (рис. 4.7, б) названа так, потому что она параллельна системе координат SЛxЛyЛzЛ левого снимка. У нее ось ZM совмещена с осью zЛ, а оси XМ и YМ параллельны осям xЛ и yЛ, соответственно.
В базисной системе координат из элементов ориентирования (4.6) пары снимков равны нулю три угловых элемента ориентирования: Л' = ' = ' = 0. В результате в базисной системе координат для пары снимков число элементов ориентирования, не равных нулю, сокращается до шести:
Л', Л', b, П', П', П'. (4.7)
В системе координат левого снимка равны нулю все шесть элементов ориентирования этого снимка: XМSл = YМSл = ZМSл = Л' = Л' = Л' = 0. Следовательно, в этой системе координат для пары снимков число элементов ориентирования, не равных нулю, будет также равно шести:
b, ', ', П', П', П'. (4.8)
Как видно, в обеих системах координат модели объекта элементы ориентирования (4.7) и (4.8) пары снимков, не равные нулю, состоят из линейного элемента (базиса проектирования b) и пяти угловых элементов. Угловые элементы называют элементами взаимного ориентирования пары снимков и используют при построении модели объекта, что рассматривается в 6.3.
4.8. Определение элементов внешнего ориентирования снимков во время съёмки
Если в ходе фотосъёмки для каждого снимка будут определены элементы внешнего ориентирования: координаты центра проекции и три угла, то это исключит дорогостоящий, трудоемкий процесс полевой привязки снимков, сократит фотограмметрическую обработку снимков и, тем самым, ускорит сроки создания топографических карт. При наземной стереотопографической съёмке привязка фотостанций к пунктам государственной геодезической сети не составляет особого труда, и обеспечивается высокоточное определение элементов внешнего ориентирования снимков. Однако при аэро- и космической съёмках эта задача требует решения сложных технических проблем, которые полностью не решены.
Еще в конце 19 века предпринимались различные попытки определять положение фотокамеры, которая подвешивалась к воздушному шару. На снимок впечатывались показания барометра, по которым рассчитывали высоту фотографирования, устанавливали дополнительную фотокамеру, фотографировавшую линию горизонта, по положению которой рассчитывали угол наклона снимка (примером является телеаппарат С.А.Ульянина). Р.Ю.Тиле определял положение фотокамеры, подвешенной к воздушному шару, путем геодезических засечек теодолитами, установленными на земле. В снимок стали впечатывать изображение круглого уровня, у которого положение пузырька показывало угол наклона и азимут отклонения главной оптической оси. Предлагалось определять угол наклона снимка путем фотографирования другой камерой звездного неба. Однако в топографической аэрофотосъёмке эти способы не используются. По фотографиям линии горизонта величина угла наклона аэроснимка определяется с низкой точностью из-за влияния рефракции, дымки и рельефа местности. Что касается фотографирования звезд, то днем, когда производится топографическая аэросъёмка, звезды не видны. Кроме того, усложняется съемочная аппаратура. Оба способа можно применять при космической фотосъёмке. Основным способом при топографической аэросъёмке являлось не определение величины угла наклона, а удерживание аэроснимков в горизонтальном положении с помощью гиростабилизирующей установки, которая обеспечивала получение снимков с углами наклона, не превышающими 10, при этом 70% углов лежали в пределах 30'. Для определения углов разворота снимков в их плоскостях не требуется высокой точности, т.к. эти углы легко учитываются путем разворота снимков на приборе.
Для определения плановых геодезических координат центров проекции снимков во время аэросъёмки во второй половине 20 века применяли радиодальномерные станции (РДС), которые работали с использованием радиолокации. Комплект состоял из трёх наземных и одной самолётной станций. Наземные станции устанавливали в районе аэросъёмки и привязывали к пунктам геодезической сети. По координатам этих станций рассчитывались базисы - расстояния между станциями. Во время съёмки самолётная станция непрерывно находилась на радиосвязи с наземными станциями, и в моменты открытия затвора фотокамеры фоторегистратор фиксировал её показания на фотоплёнку. Эти показания использовались для расчёта удалённостей самолёта от каждой наземной станции. В результате получались три треугольника с известными длинами сторон. После решения треугольников вычисляли геодезические координаты центров проекции снимков. Точность расчёта равнялась примерно 5 м при дальностях от самолёта до наземных станций до 350 км. Такая точность позволяла использовать РДС при создании карт масштабов 1:25000 и мельче. При благоприятных условиях точность повышалась до 2 м, что удовлетворяло создание карты масштаба 1:10000.
С развитием спутниковых навигационных систем ГЛОНАСС (РФ) и GPS (США), а также установкой на носителе съёмочной аппаратуры инерциальных навигационных систем точность определения элементов внешнего ориентирования значительно повысилась. При благоприятных расположениях спутников над горизонтом и устойчивой связи с ними координаты центров проекции снимков определяются с точностью примерно 20 см, что позволяет использовать эти координаты при создании карт в масштабах 1:2000 и 1:1000. Современное развитие техники позволяет надеется, что в ближайшем будущем задача определения элементов внешнего ориентирования снимков в момент открытия затвора фотокамеры будет решена, и отпадёт необходимость в полевых работах по определению координат опорных точек.
5. ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ СИСТЕМ КООРДИНАТ
5.1. Технологическая схема преобразования систем координат
Фотограмметрическая обработка снимков состоит из последовательных преобразований координат. На рис. 5.1 приведена цепочка таких преобразований координат при обработке стереопары и одиночного снимка.
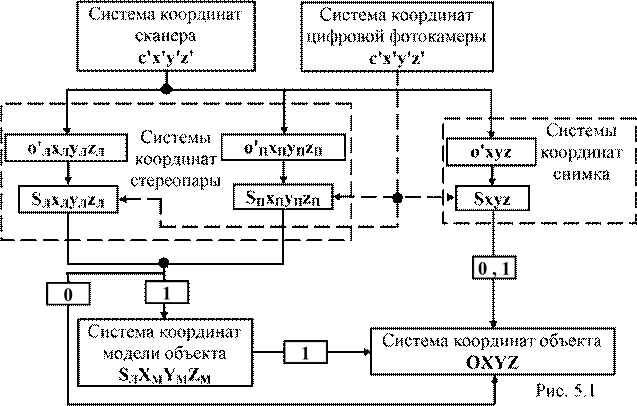
Координаты точек стереопары вначале переводят из системы координат c'x'y'z' сканера в системы координат левого o'ЛxЛyЛzЛ и правого o'ПxПyПzП снимков, а затем в системы координат SЛxЛyЛzЛ и SПxПyПzП, соответственно.
Для снимка преобразование выполняется аналогично: сначала из системы координат c'x'y'z' сканера в систему координат o'xyz, а затем в систему координат Sxyz.
Если снимок получен с помощью цифровой фотокамеры, то сразу выполняется переход из системы координат c'x'y'z' матрицы ПЗС в системы координат SЛxЛyЛzЛ и SПxПyПzП для пары снимков и в систему координат Sxyz для одиночного снимка (указано пунктирной линией).
Координаты точек стереопары и снимка можно преобразовать сразу в систему координат OXYZ объекта, если известны с достаточной точностью элементы внешнего ориентирования снимков, определяющие их положения в пространстве координат объекта (преобразование обозначено цифрой 0).
Если элементы внешнего ориентирования одиночного снимка неизвестны или известны с недостаточной точностью, то с помощью опорных точек, координаты которых известны в системе координат объекта, вычисляют элементы внешнего ориентирования снимка, а затем осуществляют переход в систему координат OXYZ объекта (этот вариант обозначен цифрой 1).
Для стереопары при таких же условиях координаты точек пересчитывают из систем координат SЛxЛyЛzЛ и SПxПyПzП в систему координат SЛXМYМZМ модели объекта. Затем, используя опорные точки, вычисляют элементы внешнего ориентирования модели и пересчитывают координаты из системы координат SЛXМYМZМ модели в систему координат OXYZ объекта (этот вариант обозначен цифрой 1).
5.2. Преобразование координат из системы координат сканера в систему координат снимка с началом в его центре проекции
Преобразование координат точек снимка из системы координат c'x'y'z' сканера в систему координат Sxyz снимка выполняют в два этапа. На первом этапе координаты преобразуют в систему координат o'xyz снимка с началом в его плоскости. Т.к. у обеих систем координат z' = z = 0, используют формулы для плоских систем координат. На втором этапе координаты преобразуют в систему координат Sxyz снимка с началом в его центре проекции.
![]()
![]()
![]()
![]() Первый
этап выполняют следующим образом (рис. 5.2). Положение начала o'
системы координат o'xy снимка
Первый
этап выполняют следующим образом (рис. 5.2). Положение начала o'
системы координат o'xy снимка
y' в системе координат c'x'y' определяет-
ся вектором r'o' , а положение точки m
снимка - вектором r'. Положение точки m в системе координат o'xy опреде-
ляется вектором r . Величины векторов o' и r' известны. Величина вектора r является искомой и из треугольника
![]() векторов равна r = r'
- r'o' .
Спроектировав векторы r' и r'o' на коорди-
векторов равна r = r'
- r'o' .
Спроектировав векторы r' и r'o' на коорди-
c' натные оси x' и y', а вектор r на коор-
динатные оси x и y, получим координаты векторов:
![]()
Рис. 5.2 r![]() ' x', y', r'o'
x'o', y'o', r
' x', y', r'o'
x'o', y'o', r![]() x, y. С учётом
того, что систему координат c'x'y' нужно повернуть на угол ' до
положения, когда она встанет параллельно системе координат o'xy, формулы
преобразования координат точек снимка из системы координат c'x'y' в систему
координат o'xy имеют вид:
x, y. С учётом
того, что систему координат c'x'y' нужно повернуть на угол ' до
положения, когда она встанет параллельно системе координат o'xy, формулы
преобразования координат точек снимка из системы координат c'x'y' в систему
координат o'xy имеют вид:
x x'x'о cosκ' sinκ'x'x'о
y Aκ' y'y'оsinκ' cosκ'y'y'о. (5.1) В (5.1) неизвестны угол разворота ' и координаты x'о', y'о'. Их значения можно определить по измеренным координатам x'i, y'i координатных меток, где I - номер метки. Т.к. ось х фиксируется координатными метками 1 и 2, угол ' можно вычислить по формуле
![]() ' = arctg y'2
y'1 .
(5.2) x'2 x'1
' = arctg y'2
y'1 .
(5.2) x'2 x'1
![]()
![]()
![]()
![]() Т.к.
началом системы координат o'xy является точка пересечения линий 1-2 и 3-4, для
каждой линии составим уравнение прямой, проходящей через две координатные метки
и точку o'. x'2x'1 y'2y'10,x'3x'4 y'3y'4
0. (5.3)
Т.к.
началом системы координат o'xy является точка пересечения линий 1-2 и 3-4, для
каждой линии составим уравнение прямой, проходящей через две координатные метки
и точку o'. x'2x'1 y'2y'10,x'3x'4 y'3y'4
0. (5.3)
x'o'x'1 y'o'y'1x'o'x'4 y'o'y'4
Из совместного решения этих уравнений находим
![]() x
, y'o' = y
,
x
, y'o' = y
,
x'o' =
![]()
![]()
![]() x'
y' - x' y'1 2 2
1 x' - x'x' - x'14 23
,
y y' -
y'y' - y'32 41 x'
y' - x' y'x' y' - x' y'41 23 32
14,
x'
y' - x' y'1 2 2
1 x' - x'x' - x'14 23
,
y y' -
y'y' - y'32 41 x'
y' - x' y'x' y' - x' y'41 23 32
14,
xx' y' - x' y'4 3 3 4
где
![]()
y' - y'2 1 x'
- x'1 2.
y' - y'2 1 x'
- x'1 2.
y' - y'3 4 x' - x'4 3
Вычисленные по (5.2) и (5.3) значения ' и x'о', y'о' подставляют в (5.1) и рассчитывают координаты x, y точек снимка в его системе координат о'xyz. На этом завершается первый этап преобразования координат.
На втором этапе вычисленные координаты x, y, z = 0 дополняют элементами внутреннего ориентирования x0, y0, f и получают координаты x-x0, y-y0, z = -f точек снимка в системе координат Sxyz.
5.3. Преобразование координат из систем координат стереопары в систему координат объекта
При выполнении этого процесса исходными являются координаты
(х-xо)Л, (у-уо)Л, zЛ = -f точки m левого снимка (рис. 5.3) в системе координат

SЛxЛyЛzЛ и координаты (х-xо)П, (у-уо)П, zП = -f точки m' правого снимка в системе координат SПxПyПzП. Необходимо по этим координатам вычислить координаты X, Y, Z точки М объекта.
В системе координат OXYZ объекта положение точки М определяется
![]()
![]()
вектором R, положение центра проекции SЛ левого снимка - вектором RSл . В то же время положение точки М относительно центра проекции SЛ левого
![]()
снимка задаётся вектором Rл . Векторы R, RSл и Rл составляют треугольник, и связь между ними следующая:
![]()
R= RSл + Rл . (5.4)
![]()
![]() Положение
точки m на левом снимке определяется вектором rл , который является
коллинеарным с вектором Rл . Связь между
этими векторами опреде-
Положение
точки m на левом снимке определяется вектором rл , который является
коллинеарным с вектором Rл . Связь между
этими векторами опреде-
![]()
ляется зависимостью Rл = Nrл , где N - скалярный множитель, представляющий собой с точки зрения фотограмметрии масштабный коэффициент. С учётом такого соотношения векторов формула (5.4) будет иметь следующий вид:
![]()
![]()
R = RSл + Nrл . (5.5)
Формула (5.5) представляет собой формулу перехода от точек снимка к точкам объекта в вектором виде. Чтобы заменить вектора координатами, введем системы координат SЛx0Лy0Лz0Л левого и SПx0Пy0Пz0П правого снимков, которые параллельны системе координат OXYZ объекта и являются системами координат горизонтальных снимков (углы ω = α = κ = 0). Спроектируем векто-
![]()
ры R и RSЛ на оси координатной системы OXYZ, а вектор rл на оси координатной системы SЛx0Лy0Лz0Л. В результате векторное уравнение (5.5) запишем в координатной форме
XY XYSS xoo . (5.6)
Z ZS л zo л
|
x x xo c11 y oл A л л л y fyoл cc3121 zo |
c12 c22 c32 |
c13x xo c23y yo , (5.7) c33 f л |
Координаты x0Л, y0Л, z0Л точек на левом горизонтальном снимке неизвестны, но известны координаты (х-x0)Л, (у-у0)Л, zЛ = -f точек, измеренные на левом наклонённом снимке в системе координат SЛxЛyЛzЛ. Преобразование координат из этой системы координат в систему координат SЛx0Лy0Лz0Л выполняют с использованием угловых элементов внешнего ориентирования левого снимка. o
где A л л л - матрица поворота системы координат SЛxЛyЛzЛ до положения системы координат SЛx0Лy0Лz0Л, cij - направляющие косинусы, величины которых зависят от угловых
элементов внешнего ориентирования левого снимка: Л, Л, Л.
Подставив (5.7) в (5.6), получим формулы перехода из систем координат SЛxЛyЛzЛ и SПxПyПzП в систему координат OXYZ объекта.
X XS c11 c12 c13 x xo
Y YS N c 21 c22 c23 y yo . (5.8)
Z ZS Л c31 c32 c33 f Л
В системе координат SЛXYZ, параллельной системе координат ОХУZ, XSЛ = YSЛ = ZSЛ = 0 и формулы (5.8) имеют вид:
X c11 c12 c13x x0
Y Nc21 c22 c23y y0 . (5.9)
Z c31 c32 c33 f Л
В (5.8) и (5.9) масштабный коэффициент N неизвестен. Для его определения используем базис фотографирования В и результаты измерения правого снимка. Векторы Rп и rп (см. рис. 5.3) коллинеарны и их векторное произве-
![]()
![]() дение
Rп rп = 0. Т.к. Rп = Rл - B = Nrл - B,
векторное произведение запишем в виде: (Nrл -B)rп = 0. Раскрыв
скобки и переставив второе векторное
дение
Rп rп = 0. Т.к. Rп = Rл - B = Nrл - B,
векторное произведение запишем в виде: (Nrл -B)rп = 0. Раскрыв
скобки и переставив второе векторное
![]()
произведение в правую часть равенства, получим N(rл rп ) = Brп , а затем формулу расчёта масштабного коэффициента в векторном виде.
![]() N Brп .
(5.10) rл rп
N Brп .
(5.10) rл rп
![]()
Спроектируем вектор B на координатные оси системы OXYZ, а векторы
![]()
rл и rп на координатные оси систем SЛx0Лy0Лz0Л и SПx0Пy0Пz0П, соответственно.
![]()
![]()
В результате получим координаты векторов: B BX, BY, BZ; rл x0Л, y0Л, z0Л;
![]()
rп x0П, y0П, z0П. Подставив эти координаты в (5.10), получим
0,5
2 2 2
![]() BY zBZп BoZ xBoXп
xBoXп yBoYп
BY zBZп BoZ xBoXп
xBoXп yBoYп
yoп o z п
N z л 2 o xoл 2 xoл yoл 2 . (5.11)
yoл o z л
o zoп zoп xoп xoп yoп
y п
После раскрытия определителей формула (5.11) принимает вид:
0,5
(B
![]() N
Y zоп
B yZ оп)2 (B xZ оп BX zоп)2 (BX yоп BY xоп)2 ,
(5.12)
N
Y zоп
B yZ оп)2 (B xZ оп BX zоп)2 (BX yоп BY xоп)2 ,
(5.12)
(yолzоп yопzол)2 (xопzол xолzоп)2 (xолyоп xопyол)2 где xоо x xo xоо A п п п xy xyoo . (5.13)
y A л л л y yo , y
zол f л zоп f п
Подставив (5.13) в (5.12), а (5.12) в (5.8) и (5.9), получим развёрнутые формулы перехода из систем координат SЛxЛyЛzЛ и SПxПyПzП пары снимков в системы координат OXYZ и SЛXYZ.
5.4. Формулы направляющих косинусов
![]()
![]()
![]() В
формулах (5.7) - (5.13) участвуют направляющие косинусы cij, значения которых зависят
от величин и знаков угловых элементов внешнего ориентирования , , снимков. В 4.6
указано, что углы ,
, имеют знак
плюс, если в момент съёмки система координат снимка выполнила повороты против
хода часовой стрелки вокруг трёх координатных осей от положения, при котором
она была параллельна системе координат объекта. С учётом этого на рис. 5.4 oz y
В
формулах (5.7) - (5.13) участвуют направляющие косинусы cij, значения которых зависят
от величин и знаков угловых элементов внешнего ориентирования , , снимков. В 4.6
указано, что углы ,
, имеют знак
плюс, если в момент съёмки система координат снимка выполнила повороты против
хода часовой стрелки вокруг трёх координатных осей от положения, при котором
она была параллельна системе координат объекта. С учётом этого на рис. 5.4 oz y
y
x S
x , x yo x y, yРис. 5.4 z, z x
показаны три последовательных поворота системы координат снимка от положения горизонтальной системы координат Sxoуozo через положения Sxyz
(поворот на угол ) и Sxyz (поворот на угол ) до положения наклонённой системы координат Sxyz снимка (после поворота на угол ). В таблице 5.1 с учётом рис. 5.4 приведены величины углов между осями координат при каждом повороте.
Таблица 5.1
|
1-й поворот на угол |
2-й поворот на угол |
3-й поворот на угол |
|||||||||
|
Ось |
xo |
yo |
zo |
Ось |
x |
y |
z |
Ось |
x |
y |
z |
|
x |
0 |
90O |
90O |
x |
|
90O |
90O+ |
x |
|
90O- |
90O |
|
y |
900 |
|
90O- |
y |
90O |
0 |
90O |
y |
90O+ |
|
90O |
|
z |
900 |
90O+ |
|
z |
90O- |
90O |
|
z |
90O |
90O |
|
Используя таблицу, составим матрицы трёх поворотов.
1 0 0 cos 0 sin cos sin 0
A0 cos sin, A 0 1 0 , A sin cos 0. (5.14)
0 sin cos sin 0 cos 0 0 1
При фотограмметрической обработке снимков нужно выполнить повороты наклонённой системы координат снимка Sxyz на углы , , до положения горизонтальной системы координат Sx0y0z0. Это выполняется по формулам
|
т т xo = A A Aт xy = A xy = cc1121 y zo z z c31 |
c12 c22 c32 |
c13 x c23 y , (5.15) c33 z |
o
где A , Aт, Aт - матрицы, транспонированные к матрицам (5.14). Следоват
тельно, матрица A будет равна следующему произведению матриц:
c11 c12 c13 1 0 0 cos 0 sincos sin 0 c21 c22 c230 cos sin 0 1 0 sin cos 0.
c31 c32 c33 0 sin cossin 0 cos 0 0 1
Перемножив матрицы, получим формулы вычисления величин направляющих косинусов:
|
c11 cos cos c12cos sin c13 sin c21 cos sin sin sin cos c22 cos cos sin sin sin |
c23 sin cos c31 sin sin cos sin cos c32 sincoscos sin sin c33 cos cos |
(5.16) |
Направляющие косинусы позволяют вычислить угловые элементы внешнего ориентирования снимка по формулам:
c23 , = arcsin c13, = -arctg c12 . (5.17)
= -arctg
c33 c11
Направляющие косинусы связаны следующими независимыми уравнениями, которые используют для контроля определения их величин:
c1122 cc122222cc13232211 c cc c11 3111 21 cc12 3212 22cc cc13 3313 23cc 00 (5.18) c21
c312 c322 c332 1 c21 31c c22 32c c23 33c 0
5.5. Преобразование координат из систем координат стереопары идеального случая аэросъёмки в систему координат объекта
Идеальный случай аэросъёмки подразумевает следующие условия.
1. Базис фотографирования B параллелен координатной оси Х, поэтому его проекции на координатные оси BX = B, BY = BZ = 0.
2. Снимки расположены горизонтально, т.е. углы Л = Л = Л = П = П = П = 0, и системы координат левого SЛx0Лy0Лz0Л и правого SПx0Пy0Пz0П снимков параллельны системе координат ОХУZ объекта.
После подстановки значений базиса и углов в (5.8) и (5.9) матрица A превращается в единичную, а масштабный коэффициент рассчитывается по формуле:
B B
![]() N = , xoл
xoп po
N = , xoл
xoп po
где x0Л, x0П - координаты точек на левом и правом горизонтальных снимках, р0 - продольный параллакс (см. 4.5).
Т.к. получить горизонтальные снимки в полёте практически невозможно, положения точек на них находят путём вычислений. При этом координаты главной точки xо = yо = 0. С учётом сказанного формулы перехода из систем координат стереопары идеального случая аэросъёмки в систему координат объекта будут иметь вид в системе координат OXYZ
XY XYSS B xoo XYSS + Bo xyoo , (5.19)
![]()
![]()
Z ZS л xo л xoп yf л ZS л p f л
и в системе координат SЛXYZ
![]()
![]() X B
xyoo B
xyoo .
(5.20)
X B
xyoo B
xyoo .
(5.20)
YZ x л п f л po f л o xo
B B
![]() Смысл коэффициента можно
определить из формулы для xoл xoп po
Смысл коэффициента можно
определить из формулы для xoл xoп po
B Z
![]() координаты Z. Запишем . Учитывая,
что расстояние вдоль отвесной po f
координаты Z. Запишем . Учитывая,
что расстояние вдоль отвесной po f
линии между центром проекции S и определяемой точкой является высотой фотографирования H и значение её находится в отрицательной области координатной оси Z, заменим Z на -H. В результате получим
B H
![]() m,
(5.21) po f
m,
(5.21) po f
где m - знаменатель масштаба съёмки. Таким образом, масштаб съёмки определяется формулой
1 f 1
![]() .
(5.22) m H H f
.
(5.22) m H H f
Т.к. высота фотографирования Н над точками, изобразившимися на снимке, меняется из-за рельефа местности, можно сделать вывод, что масштаб съёмки в пределах снимка величина переменная. Только на горизонтальном снимке, на котором изобразилась плоская горизонтальная местность, масштаб будет одинаковым во всех точках.
С учётом (5.21) формулы (5.20) можно записать в следующем виде:
X ![]() Bo xoл
Bo xoл ![]() Zf
xoл
Zf
xoл ![]() Hf
xoл; p
Hf
xoл; p
Y ![]() pBo yo
pBo yo
![]() Z yoл
Z yoл ![]() Hf yoл;
(5.23) л f
Hf yoл;
(5.23) л f
B Z ![]() f po
f po
Чтобы понять причины появления продольного параллакса, воспользуемся из (5.23) формулой координаты Z для вывода формулы расчёта продольного параллакса с учётом (5.21). В результате будем иметь.
![]() po B f B f B b.
(5.24)
po B f B f B b.
(5.24)
Z H m
Из (5.24) следует, что продольный параллакс является базисом фотографирования в масштабе съёмки. С увеличением (уменьшением) базиса фотографирования В увеличивается (уменьшается) продольный параллакс. С изменением рельефа местности высота фотографирования Н изменяется и, следовательно, изменяется величина продольного параллакса. Когда на стереопаре идеального случая аэросъёмки сфотографирована плоская горизонтальная местность, высоты фотографирования для всех точек будут одинаковы, и продольный параллакс будет постоянным.
Что касается поперечного параллакса q = yЛ - yП, то он возникает из-за различия в величинах элементов внешнего ориентирования левого и правого снимков. BX = XSп - XSл не изменяет координат уП по сравнению с координатами уЛ и, следовательно, не вызывает появления поперечного параллакса. BY = YSп - YSл вызывает изменение ординаты на правом снимке на величину
B fY . BZ = ZSп - ZSл вызывает изменение масштаба правого снимка относитель-
H
но левого. Углы ЛП, ЛП, ЛП вызывают изменения координат на правом снимке относительно левого.
5.7. Формула превышений
Предположим, что на двух точках стереопары идеального случая аэросъёмки измерены продольные параллаксы р01, p02 и по формуле (5.23) для коор-
Bf Bf
динаты Z вычислены их высоты на местности: Z1
= - ![]() po
и Z2 = -
po
и Z2 = - ![]() po2
. Опреде-
po2
. Опреде-
1
лим превышение точки 2 над точкой 1.
Bf(po
![]() h
Z2 Z1 po o2p2po1)
Z (p1 poo22 po1) . (5.25)
h
Z2 Z1 po o2p2po1)
Z (p1 poo22 po1) . (5.25)
1
Введем понятие разность продольных параллаксов: р0 = р02 - р01. Тогда p02 = p01 + p0. Заменим -Z1 на H1. Подставив указанные величины в (5.25), получим формулу расчёта превышений между парой точек на местности.
![]() hpoH p11
op . (5.26) o
hpoH p11
op . (5.26) o
Формула (5.26) является строгой только для снимков идеального случая аэросъёмки. С увеличением значений элементов внешнего ориентирования пары снимков ошибки вычислений по этой формуле будут возрастать. Для расчёта по плановым аэроснимкам небольших превышений между точками равнинно-всхолмленной местности можно использовать приближённую формулу. В знаменателе формулы (5.26) p0 можно опустить по малости по сравнению с величиной р01, которая с учётом формулы (5.24) равна базису фотографирования в масштабе съёмки точки 1. Кроме того, опустим верхний и нижний индексы и в результате получим следующую формулу:
H
h ![]() p. (5.27)
b
p. (5.27)
b
Эту формулу можно использовать при работе со стереоскопом и параллаксометром. Например, наводят марку на вершину дерева и на землю, снимая отсчёты со шкалы параллактического винта. Разность отсчётов даст значение p, которое подставляют в формулу (5.27) и вычисляют высоту дерева.
5.8. Формулы преобразования координат между системами координат наклонного снимка и объекта
В фотограмметрии используют два варианта формул преобразования координат между системами координат наклонного снимка и объекта.
Первый вариант это преобразование координат из системы координат снимка в систему координат объекта. Эти формулы обеспечивают вычисление координат точек на объекте по координатам, измеренным на снимке.
Второй вариант по сравнению с первым вариантом является обратным преобразованием координат из системы координат объекта в систему координат снимка. Эти формулы позволяют по координатам точек объекта и заданным значениям элементов ориентирования снимка рассчитать безошибочные координаты точек снимка. Это делают, например, при определении ошибок снимка, нанесении на снимок контуров будущих зданий, чтобы определить их положение относительно существующих строений, и тому подобное.
Формулы первого варианта можно получить из формул (5.8), опустив индекс "л".
X XS x x o XS c11 12 13c c x x o
YZ YZSSNAy yf oYZSSN cc31 32 3321 22 23cc cc y yf o. (5.28)
Т.к. базис фотографирования и второй снимок отсутствуют, значение N можно определить только, если известны высоты Z точек. Таким образом, следует вывод, что по одному снимку определить три координаты для точек объекта невозможно. Определим масштабный коэффициент N из формул (5.28), используя формулу для координаты Z.
![]() Z-ZS .
(5.29)
Z-ZS .
(5.29)
N=
c31(x x )o c32(y y )o c33f
Подставив (5.29) в (5.28) для координат X и Y, получим формулы вычисления плановых координат точек объекта в его системе координат по координатам точек наклонного снимка.
X XS (Z Z )S cc3111((xx x )x )oo cc1232((yy y )y )oo cc1333ff (5.30)
Y YS (Z Z )S c21(x x )o c22(y y )o c23f c31(x x )o c32(y y )o c33f
Если координаты точек объекта нужно определить в системе координат SXYZ, то в формулах (5.30) приравняем XS = YS = ZS = 0. Кроме того, заменим Z на -H и в результате получим:
X H cc3111((xx x )x )oo cc1232((yy y )y )oo cc1333ff (5.31)
Y H c21(x x )o c22(y y )o c23f c31(x x )o c32(y y )o c33f
Для вывода формул второго варианта преобразуем формулы (5.28) на обратные, т.е. получим формулы, по которым можно рассчитать координаты точек снимка в его системе координат Sxyz по координатам точек объекта.
xy fxyoo N1ATYXZYXSS N1ccc121311 ccc222321 ccc323331YXZYXZSSS. (5.32)
ZS
Из (5.32) выпишем формулу для -f.
f N1[c13(X X )S c23(Y Y )S c33(Z Z )]S .
Из неё получим формулу расчёта масштабного коэффициента
N-1= ![]() f c13(X X )S c23(Y Y )S c33(Z Z )S
f c13(X X )S c23(Y Y )S c33(Z Z )S
и подставим её в два первых уравнения в (5.32). В результате получим формулы расчёта по координатам точек объекта координат точек наклонного снимка в системе координат o'xyz.
x xo f cc1311((XX X )X )SS cc2321((YY Y )Y )SS cc3133((ZZZ )Z )SS (5.33)
y yo f c12(X X )S c22(Y Y )S c32(Z Z )S c13(X X )S c23(Y Y )S c33(Z Z )S
5.9. Преобразование координат из системы координат горизонтального снимка в систему координат объекта
Чтобы получить формулы преобразования координат из системы координат горизонтального снимка в систему координат объекта, подставим = = = 0 в направляющие косинусы в формулах (5.30) и (5.31). Кроме того, при рассмотрении идеального случая аэросъёмки отмечалось, что координаты главной точки на горизонтальном снимке равны нулю. В связи с этим координаты х-x0 и у-y0 заменим соответственно на x0 и y0, у которых верхний индекс указывает, что это координаты на горизонтальном снимке. В результате формулы перехода из системы координат горизонтального снимка в систему координат объекта будут иметь вид: в системе координат OXYZ:
![]()
![]() X = XS - (Z-Z )xS o , Y =
YS - (Z-Z )yS o
(5.34) f f
X = XS - (Z-Z )xS o , Y =
YS - (Z-Z )yS o
(5.34) f f
и в системе координат SХYZ:
Hxo Hyo
X = ![]() ,
Y =
,
Y = ![]() .
(5.35) f f
.
(5.35) f f
5.10. Преобразование координат из системы координат наклонного снимка в систему координат горизонтального снимка,
имеющих общий центр проекции
Если наклонный и горизонтальный снимки получены одной и той же фотокамерой из одного центра проекции, то формулы преобразования координат точек из системы координат Sxyz наклонного снимка в систему координат Sx0y0z0 горизонтального снимка будут следующие. На обоих снимках имеется изображение одного и того же участка местности, координаты X, Y, Z точек которого, рассчитанные по формулам (5.31) и (5.35), должны быть одинаковыми. С учётом этого приравняем правые части формул (5.31) и (5.35).
Hxo H c11(x x )o c12(y y )o c13f
![]()
f c31(x x )o c32(y y )o c33f .
Hyo H c21(x x )o c22(y y )o c23f
![]()
f c31(x x )o c32(y y )o c33f
После преобразований получим
xo f cc3111((xx x )x )oo cc1232((yy y )y )oo cc1333ff . (5.36)
yo f c21(x x )o c22(y y )o c23f c31(x x )o c32(y y )o c33f
Формулы (5.36) позволяют пересчитать координаты точек наклонного снимка на плоскость горизонтального снимка, на котором изображение точек будет получено с сохранением масштаба съёмки и без влияния угла наклона снимка. Формулы (5.36) называют формулами трансформирования.
6. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ МОДЕЛИ ОБЪЕКТА
6.1. Принцип построения геометрической модели объекта
В гл. 5 были приведены формулы преобразования координат из систем координат снимков в систему координат объекта. Эти формулы позволяют решить прямую фотограмметрическую засечку и определить координаты точек объекта. Однако это возможно, если известны элементы внешнего ориентирования снимков. Если элементы внешнего ориентирования неизвестны или точность их определения низка, то задачу решают в два этапа. Вначале по стереопаре строят геометрическую модель объекта, а потом по координатам опорных точек ориентируют её в системе координат объекта и определяют элементы внешнего ориентирования снимков. Этот процесс называют обратной фотограмметрической засечкой. Далее, используя элементы внешнего ориентирования снимков, определяют координаты точек объекта, т.е. решают прямую фотограмметрическую засечку. Весь процесс называют двойной фотограмметрической засечкой.
![]() Принцип построения геометрической модели следующий.
Предположим, что при съёмке из центра проекции SЛ (рис. 6.1) был
получен снимок РЛ. Опти k' m' ческие лучи, идущие от точек объекта М и К, пройдя центр
проекции SЛ, зафиксировали на снимке РЛ их изображения в
точках m и k. После пролёта базиса фотографирования SЛSП
= В из центра проекции SП был получен второй снимок РП.
Оптические лучи, идущие от точек М и К, пройдя центр проекции SП,
зафиксировали на снимке РП их изображения в точках m' и k'. Таким
образом, для каждой точки объекта два соответственных оптических луча (в
описывае-
Принцип построения геометрической модели следующий.
Предположим, что при съёмке из центра проекции SЛ (рис. 6.1) был
получен снимок РЛ. Опти k' m' ческие лучи, идущие от точек объекта М и К, пройдя центр
проекции SЛ, зафиксировали на снимке РЛ их изображения в
точках m и k. После пролёта базиса фотографирования SЛSП
= В из центра проекции SП был получен второй снимок РП.
Оптические лучи, идущие от точек М и К, пройдя центр проекции SП,
зафиксировали на снимке РП их изображения в точках m' и k'. Таким
образом, для каждой точки объекта два соответственных оптических луча (в
описывае-
мом примере MSЛm и MSПm', KSЛk и KSПk'), а также базис фотографирования В составляют треугольник засечки, лежащий в базисной плоскости, проведённой через базис и точку объекта.
Используя принцип обратимости фотографического процесса, восстановим процесс, имевший место при съёмке. При этом соответственные проектирующие лучи пройдут путь оптических лучей в обратном направлении и пересекутся. Однако при фотограмметрической обработке нельзя имитировать съёмочный процесс в натуральном размере. Сместим правую связку проектирующих лучей в сторону левой связки параллельно самой себе, чтобы оптические лучи не выходили из своих базисных плоскостей. При этом правый центр проекции SП должен перемещаться вдоль базиса фотографирования. Установим его в положение S'П. В результате будут сохранены пересечения соответственных проектирующих лучей правой и левой связок (точки M' и K') и будет получена поверхность, соответствующая поверхности объекта, но в уменьшенном виде.
Таким образом, геометрическая модель сфотографированного объекта это поверхность, образованная точками пересечения соответственных проектирующих лучей. Расстояние SЛSП' = b называется базисом проектирования. Его отношение к базису фотографирования определяет масштаб модели.
1 b 1
. (6.1)
![]() M B B
b
M B B
b
Т.к. величину базиса фотографирования изменить нельзя, изменение масштаба модели выполняют изменением базиса проектирования.
Необходимо обратить внимание на следующее. Геометрическая модель, сохраняющая геометрию объекта, не видна оператору, а видна стереоскопическая модель, которая под действием различных источников, описанных в главе 3, представляет искажённое изображение объекта. Обе модели не совпадают друг с другом. Однако стереоскопическая модель обладает пластичностью (см. 1.2), что позволяет измерять геометрическую модель. В момент наведения стереоскопической марки на измеряемую точку стереоскопическая модель совпадает в этой точке с геометрической моделью.
Построение, ориентирование и измерение геометрической модели состоит из следующих процессов: 1) внутреннее ориентирование снимков, 2) взаимное ориентирование снимков, 3) внешнее ориентирование модели, 4) съёмка контуров и рельефа путём измерения точек модели.
6.2. Внутреннее ориентирование снимка
Геометрический смысл внутреннего ориентирования снимка заключается в том, что в результате его выполнения восстанавливается связка проектирующих лучей, которая существовала в момент экспонирования.
Математическое решение процесса заключается в преобразовании координат точек снимка в пространственную систему координат Sxyz снимка с началом в центре проекции.
Для снимков, полученных с помощью цифровой фотокамеры, внутреннее ориентирование выполнять не нужно, т.к. он включён в процесс калибровки фотокамеры. Перед измерением цифровых снимков данные калибровки фотокамеры записывают в файл фотокамеры.
Для фотоснимков, преобразованных в цифровую форму с помощью сканера, а также фотоснимков, измеряемых на аналитических фотограмметрических приборах, внутреннее ориентирование заключается в преобразовании координат из системы координат прибора в пространственную систему координат Sxyz снимка с началом в его центре проекции. Этот процесс был рассмотрен в п. 5.2. Однако он был рассмотрен при условии, что снимок получен в идеальной центральной проекции и измеренные координаты не имеют искажений. На самом деле реальный снимок не соответствует идеальной центральной проекции. Источники ошибок, вызывающих искажение снимка рассмотрены в главе 3. Среди всех источников ошибок наиболее значительные искажения вносят дисторсия объектива фотокамеры и деформация снимка. В связи с этим в ходе выполнения внутреннего ориентирования снимка в измеренные на нём координаты вводят поправки, учитывающие искажения, внесённые этими двумя источниками. Методики введения поправок рассмотрены в пп. 3.3 и 3.4, соответственно. Исправленные координаты подставляют в формулы (5.1). В результате решения этих формул координаты измеренных точек получают в системе координат Sxyz снимка.
6.3. Условие и уравнение взаимного ориентирования пары снимков
Геометрический смысл взаимного ориентирования пары снимков заключается в том, что необходимо установить связки проектирующих лучей обоих снимков относительно друг друга в положения, которые они имели во время их экспонирования. В результате соответственные проектирующие лучи должны расположиться в одной базисной плоскости и пересечься (см. п.
6.1), образуя геометрическую модель объекта.
Следовательно, условием взаимного ориентирования является распо-
![]() ложение трёх
векторов Rл , Rп и b (рис.
6.2) в одной плоскости. Такие век-
ложение трёх
векторов Rл , Rп и b (рис.
6.2) в одной плоскости. Такие век-
![]()
![]() ZM
торы называются компланарными. Призна-
ZM
торы называются компланарными. Призна-
M ком компланарности векторов является обра-
Sл щение в нуль их смешанного произведения, т.е. уравнение взаимного ориентирования в векторном виде будет следующим:
b(RлRп)b(rлrп)0. (6.2)
Чтобы перейти от векторов к координатам, необходимо определить, в какой системе координат должна быть построена геометри-
ческая модель. В п. 4.7 указывалось, что для построения модели используют базисную систему координат или систему координат левого снимка и что для задания положений пары связок проектирующих лучей необходимо знать значения не равных нулю шести элементов ориентирования (4.7) или (4.8). Линейный элемент - базис проектирования - определяет масштаб модели (формула 6.1). Как сказано в 4.7, пять угловых элементов называют элементами взаимного ориентирования, т.к. они задают ориентацию связок проектирующих лучей относительно друг друга в заданной системе координат.
Таким образом, элементы взаимного ориентирования
'Л, 'Л, 'П, 'П, 'П (6.3)
определяют положения обеих связок проектирующих лучей в базисной системе координат SЛXMYMZM, а элементы взаимного ориентирования
', ', 'П, 'П, 'П, (6.4)
определяют положения базиса проектирования и правой связки проектирующих лучей в системе координат левого снимка SЛXMYMZM.
![]()
![]()
Спроектировав векторы b, rл и rп на оси координатной системы SЛXМYМZМ модели, получим их координаты:
![]()
![]()
![]()
b bX, bY, bZ, rл x'Л, y'Л, z'Л, rп x'П, y'П, z'П. Запишем смешанное произведение (6.2) в виде определителя:
![]()
![]() b 0 0
b 0 0
для базисной системы координат x'л y'л z'л0 (6.5)
x'п y'п z'п
и для системы координат левого снимка с учётом формул (4.2)
![]()
![]()
![]() bx by bzbcos 'cos ' bcos
'sin ' bsin
'
bx by bzbcos 'cos ' bcos
'sin ' bsin
'
x'л y'л z'л x'л y'л z'л = 0 (6.6) x'п y'п z'пx'п y'п z'п
Базис проектирования не может равняться нулю, поэтому, разделив (6.5) и (6.6) на b, после раскрытия определителей получим уравнения взаимного ориентирования в базисной системе координат
y'Л z'П - y'П z'Л = 0 (6.7)
и в системе координат левого снимка
(y'Лz'П - y'Пz'Л)cos'cos' + (x'Пz'Л - x'Лz'П)cos'sin' + (x'Лy'П - x'Пy'Л)sin' = 0. (6.8)
Координаты x', y', z' вычисляют по формулам:
в базисной системе координат ('Л = 0)
x' x xo x' x xo
y' A 'л 'л y yo , y'z' A 'п 'п 'п y fyo п , (6.9)
z' л f л п
и в системе координат левого снимка ('Л = 'Л = 'Л = 0)
x' x xo x' x xo
y'z' y fyoл , y'z' п A 'п п п' ' y fyoп ,. (6.10) л
В этих уравнениях матрицы поворота получают путём подстановки элементов взаимного ориентирования (6.3) или (6.4) в направляющие косинусы уравнений (5.16) вместо углов , , .
6.4. Аналитическое решение взаимного ориентирования
В задачу аналитического решения взаимного ориентирования входит, используя координаты точек стереопары:
(x-xo)Л, (y-yo)Л, zЛ = -f, (x-xo)П, (y-yo)П, zП = -f, (6.11)
полученные после выполнения внутреннего ориентирования в системах координат SЛxЛyЛzЛ левого и SПxПyПzП правого снимков, вычислить координаты точек модели в её системе координат SЛXMYMZM.
Решение проводят в два этапа:
1) вычисляют элементы взаимного ориентирования снимков в системе координат модели,
2) используя значения этих элементов, вычисляют координаты точек модели в её системе координат.
Этап 1. Элементы взаимного ориентирования вычисляют, используя уравнение (6.7) или (6.8) в зависимости от того, какая система координат выбрана для построения модели. Однако уравнение взаимного ориентирования является нелинейным относительно неизвестных, т.к. в отдельных членах уравнения содержатся два или три неизвестных. При решении такого уравнения невозможно найти значения неизвестных независимо друг от друга. Поэтому составляют новое уравнение, имеющее в каждом члене только одно неизвестное - поправку к приближённому значению данного элемента взаимного ориентирования. Исходные приближённые значения элементов взаимного ориентирования обычно приравнивают нулю или выбирают исходя из условий съёмки.
Обозначим искомые элементы взаимного ориентирования через i, их приближённые значения через 'i и поправки к последним через i. Эти три величины связаны зависимостью i = 'i + i, где i = 1, 2, 3, 4, 5.
Уравнение взаимного ориентирования запишем в виде функции F(i) = 0. Линеаризацию этого уравнения выполняют путём нахождения частных производных по каждому из элементов взаимного ориентирования и используют их в качестве коэффициентов при неизвестных поправках. Таким образом, линеаризованное уравнение поправок будет иметь вид:
a1 1 + a2 2 + a3 3 + a4 4 + a5 5 + ln = vn, (6.12)
где коэффициенты ai = F(i)/i - частные производные; i - порядковый номер неизвестного, равный от 1 до 5;
ln = F('i) - свободный член, вычисляемый путём подстановки в уравнение
F(i) = 0 приближённых значений 'i;
n - число уравнений или число измеренных точек.
В уравнении (6.12) пять неизвестных. Для их вычисления необходимо составить систему из пяти уравнений. Т.к. одна точка стереопары позволяет составить одно уравнение (6.12), нужно измерить не менее пяти точек. Обычно измеряют шесть точек, расположенных по одной в так называемых шести "стандартных зонах" стереопары: в углах и рядом с главными точками снимков. При измерении шести и более точек решение системы уравнений проводят по методу наименьших квадратов. При измерении 12 точек (по две точки рядом) точность определения элементов взаимного ориентирования повышается на 50. Измерение 18 точек (по три точки рядом) даёт дальнейшее небольшое (1015%) повышение точности. Измерение большего числа точек не целесообразно, т.к. увеличивается время на измерения, вычисления, поиск ошибочно измеренных точек, кроме того, возрастает процент ошибочных измерений. Составляют систему из уравнений поправок (6.12)
|
a11 a12 a13 . a1n |
a21 a22 a23 . a2n |
a31 a32 a33 . a3n |
a41 a42 a43 . a4n |
a511 l1 v1 a522 l2 v2 a533 l3 v3 . (6.13) . 4 . . a5n5 ln vn |
Систему уравнений поправок можно записать в виде AX + L = V. Из уравнений поправок составляют систему нормальных уравнений
Aт AX + Aт L = 0, (6.14)
т
где A - транспонированная матрица A. В результате решения системы уравнений (6.14) находят значения поправок i.
Итак, порядок определения элементов взаимного ориентирования будет следующим. Координаты (6.11) и приближённые значения элементов взаимного ориентирования используют для вычисления коэффициентов ain и свободных членов ln уравнений поправок (6.13). По ним составляют нормальные уравнения (6.14) и в ходе их решения находят значения поправок i, которые прибавляют к приближённым значениям элементов взаимного ориентирования 'i.
В результате будут вычислены новые значения 'i, которые используют для составления новых уравнений поправок. Все описанные операции повторяют до того, когда значения поправок станут меньше установленной величины.
В качестве критерия точности определения элементов взаимного ориентирования используют величины остаточных поперечных параллаксов qост. = y0Л - y0П, которые должны быть меньше предельной ошибки измерения этих параллаксов, где y0Л и y0П - трансформированные ординаты левого и правого снимков с использованием формул (5.36). Например, в базисной системе координат вычисление остаточных поперечных параллаксов производят по формуле
![]()
![]() qост. zлf'zп' yyпл'' zzпл'' f(yл'zzпл''zyпп' 'zл') ,
qост. zлf'zп' yyпл'' zzпл'' f(yл'zzпл''zyпп' 'zл') ,
где координаты yЛ', zЛ', yП', zП' рассчитывают по формулам (6.9).
Отбраковку ошибочных точек проводят разными способами. Простой и распространённый способ заключается в сравнении остаточных поперечных параллаксов с предельной ошибкой их измерения. Точки, у которых остаточные поперечные параллаксы превышают эту величину, либо перемеряют, либо исключают из вычислений. Правда, этот способ не обеспечивает однозначного нахождения ошибочной точки, т.к. при решении по методу наименьших квадратов ошибка на точке, измеренной с превышением предельной ошибки, будет уменьшаться за счёт частичного перемещения её величины на другие точки. В результате на точке, измеренной с ошибкой, меньшей, но близкой к предельной, остаточный поперечный параллакс может превысить эту величину.
Этап 2. Вычислив вероятнейшие значения элементов взаимного ориентирования, приступают к вычислению пространственных координат точек модели в её системе координат SЛXMYMZM. Для этого используют формулы (5.9), в которые подставляют координаты (6.11) и вероятнейшие значения элементов взаимного ориентирования. Значение базиса проектирования выбирают произвольно. Например, его величину можно приравнять величине базиса фотографирования в масштабе снимка.
Необходимо отметить, что рельеф местности и прокладка аэросъёмочного маршрута сказываются на точности решения взаимного ориентирования. Условие взаимного ориентирования - пересечение соответственных проектирующих лучей - не всегда является достаточным. При аэросъёмке горной долины с маршрута, проложенного вдоль неё, точки местности, изображения которых располагаются в стандартных зонах стереопары, и центры проекции снимков могут оказаться на цилиндрических или конических поверхностях. В этом случае можно смещать центр проекции снимка поперек маршрута, но углы между проектирующими лучами не будут изменяться, а будут изменяться углы наклона (в основном поперечные) аэроснимка, т.е. будут изменяться элементы взаимного ориентирования.
При решении системы уравнений (6.13) это проявится в том, что в определителе, составленном из коэффициентов при неизвестных, элементы двух строк или столбцов будут равны или пропорциональны. В результате решение системы становится неопределённым. Поэтому перед решением системы уравнений (6.13) нужно вычислить значение определителя. Если оно равно единице, то решение однозначно. Если оно меньше 0,2, то нужно выбрать для взаимного ориентирования другие точки с большими или меньшими высотами, чтобы они дальше лежали от окружности. Теоретические расчёты и практический опыт рекомендуют выполнять аэросъёмку короткофокусной фотокамерой с большим форматом кадра поперек горных долин.
6.5. Уравнения внешнего ориентирования модели объекта.
Элементы внешнего ориентирования модели
Геометрическая модель объекта, построенная в результате выполнения взаимного ориентирования, имеет произвольные масштаб и пространственную ориентацию. Поэтому в задачу внешнего ориентирования модели входит приведение модели к заданному масштабу и ориентирование её в системе координат объекта. В ходе выполнения внешнего ориентирования модели осуществляют преобразование координат точек из модельной системы координат SЛXMYMZM (рис. 6.3) в систему координат ОХУZ объекта с учётом масшта-
![]() Z ба
модели.
Z ба
модели.
Для выполнения этих преобразований используют уравнения внешнего ориентирования модели:
X XS X
Y YS A M M M Y tM , (6.15)
Z ZSл Z м
где XSл, YSл, ZSл - координаты левого центра
проекции SЛ в системе координат ОХУZ объ-
екта,
M, M, M - углы поворота системы коO Рис. 6.3 X ординат Sсистемы кооЛXрдинат ОХУZ объекта иMYMZM модели относ ительно tМ - масштабный коэффициент являются элементами внешнего ориентирования модели (ЭВОМ).
При наличии на модели опорных точек начало системы координат модели можно перенести в одну из этих точек, например, под номером один. В результате уравнения (6.15) примут вид:
X X1 Xi X1
Y Y1 Aωмαмκм Yi Y1 tм, (6.16)
Z Z1 Zi Z1 м
где X1, Y1, Z1 - координаты опорной точки 1 в системе координат ОХУZ; XM1, YM1, ZM1 - координаты точки 1 на модели в системе координат SЛXMYMZM.
Матрицу Aммм поворота системы координат модели составляют из направляющих косинусов, зависящих от угловых элементов внешнего ориентирования M, M, M модели. Их подставляют в (5.16) вместо углов , и вычисляют значения направляющих косинусов.
Для вычисления семи ЭВОМ необходимо составить систему из семи уравнений (6.15). Одна опорная точка с координатами X, Y, Z позволяет составить три уравнения. Следовательно, для нахождения семи неизвестных нужно иметь три (7:3 = 2,3 3) опорные точки.
6.6. Аналитическое решение внешнего ориентирования модели Внешнее ориентирование модели выполняют в два этапа:
1) используя расхождения известных и вычисленных координат опорных точек, по уравнениям (6.15) или (6.16) определяют ЭВОМ;
2) вычисленные значения ЭВОМ подставляют в уравнения (6.15) или (6.16) и перевычисляют координаты точек модели из её системы координат в систему координат объекта.
Этап 1. Т.к. уравнения (6.15) и (6.16) являются нелинейными относительно неизвестных, то берут частные производные по каждому из ЭВОМ и используют их в качестве коэффициентов при неизвестных. В качестве неизвестных используют не сами элементы, а поправки к их приближённым значениям, величины которых устанавливают в соответствии с условиями съёмки или приравнивают нулю. В результате вместо уравнений (6.15) получают уравнения поправок следующего вида:
![]()
![]()
![]()
![]()
![]() X X X X X XS
M M M tM
X' X
VX
X X X X X XS
M M M tM
X' X
VX
XS M M M tM
Y Y Y Y Y
![]()
![]()
![]()
![]()
![]() YS M M M tM
Y' Y
VY ,
(6.17)
YS M M M tM
Y' Y
VY ,
(6.17)
YS M M M tM
![]()
![]()
![]()
![]()
![]() Z Z Z Z Z ZS
M M M tM
Z' Z
VZ
Z Z Z Z Z ZS
M M M tM
Z' Z
VZ
ZS M M M tM
где X', Y', Z' - координаты опорных точек, вычисленные по приближённым значениям ЭВОМ;
Х, Y, Z - истинные координаты опорных точек.
Если используют уравнения (6.16), то после их линеаризации получают уравнения вида:
X X X X
![]()
![]()
![]()
![]() M M M tM M X' (X X )1 VX
M M M t
M M M tM M X' (X X )1 VX
M M M t
Y Y Y Y
![]()
![]()
![]()
![]() M M M t
M M M t
M M M tM M Y' (Y Y )1 VY , (6.18)
Z Z Z Z
![]()
![]()
![]()
![]() M M M tM M
Z' (Z
Z )1 VZ M M M t
M M M tM M
Z' (Z
Z )1 VZ M M M t
где X', Y', Z' - приращения координат опорных точек относительно первой, вычисленные по приближённым значениям ЭВОМ. При числе опорных точек большем, чем три, число уравнений поправок будет превышать число неизвестных, и задача решается по методу наименьших квадратов. Составив систему уравнений поправок
AX + L = V, (6.19)
составляют нормальные уравнения: Aт AX + Aт L = 0, которые решают под условием [VV] = min, и находят поправки к приближённым значениям ЭВОМ. Прибавив поправки к приближённым значениям неизвестных, находят новые значения ЭВОМ, которые используют для составления новой системы уравнений поправок (6.19). Далее решение повторяют до тех пор, пока величины поправок и свободных членов станут меньше установленных допусков.
Этап 2. Вычисленные значения ЭВОМ подставляют в уравнения (6.15) или (6.16) и перевычисляют координаты точек модели из её системы координат SЛXMYMZM в систему координат ОХУZ объекта.
6.7. Вычисление элементов внешнего ориентирования снимка
Элементы внешнего ориентирования снимка можно вычислить 1) по опорным точкам и 2) с использованием элементов взаимного ориентирования стереопары и элементов внешнего ориентирования модели.
1. При вычислении элементов внешнего ориентирования снимка по опорным точкам используют уравнения (5.30), содержащие также три элемента внутреннего ориентирования, значения которых уточняют одновременно с определением ЭВО. Уравнения приводят к линейному виду и составляют уравнения поправок.
X X X X X X X X
![]()
![]() XS XS
XS XS
![]() ZS ZS
ZS ZS
![]()
![]()
![]()
f
f xo xo
f
f xo xo
![]() yo yo
yo yo
Y Y Y Y Y Y Y X' XY Vx ,
![]()
![]() YS
YS ![]() ZS
ZS ![]()
![]()
![]()
f xo
f xo ![]() yo
yo
YS ZS f xo yo
Y' Y Vy
где XS, YS, ZS, , , , f, xo, yo - поправки к приближённым значениям неизвестных элементов ориентирования снимка; коэффициенты перед поправками - частные производные по соответст-
вующему неизвестному;
X' и Y' - координаты опорных точек, рассчитанные по формулам (5.30) при подстановке в них приближённых значений элементов ориентирования; X и Y - истинные координаты опорных точек.
Изображение одной опорной точки позволяет составить два уравнения (5.30). Следовательно, для определения девяти неизвестных нужно иметь на снимке не менее пяти (9:2 = 4,5 5) опорных точек. Четыре точки располагают в углах рабочей площади снимка (см. 1.4), а пятую точку - в центре снимка.
Если опорных точек больше пяти, то по уравнениям поправок составляют нормальные уравнения и из решения этих уравнений под условием [vv] = min находят значения поправок. Прибавив их к приближённым значениям элементов ориентирования, получают новые приближённые значения этих элементов и, используя их, вычисляют коэффициенты при искомых поправках, а также координаты X' и Y'. Вычисленные значения подставляют в уравнения поправок и повторяют решение. С увеличением числа приближений величины поправок и разности координат X'-X и Y'-Y стремятся к нулю. Вычисления считаются законченными, если на опорных точках среднее значение остаточных расхождений координат X'-X и Y'-Y не превышает 0,15 мм в масштабе карты.
2. Вычисление угловых элементов внешнего ориентирования снимка по угловым элементам взаимного ориентирования и угловым элементам внешнего ориентирования модели основано на том, что элементы взаимного ориентирования определяют угловые положения систем координат каждого снимка в системе координат модели, а её положение в системе координат объекта определяют её угловые элементы внешнего ориентирования. Следовательно, матрицы направляющих косинусов угловых элементов внешнего ориентирования левого и правого снимков можно получить следующим образом
A л л л A м м м A л ' л '
A п п п A м м м A п' п ' п '
Значения соответствующих направляющих косинусов из матриц Aллл и Aппп подставляют в формулы (5.17) и вычисляют угловые элементы внешнего ориентирования левого и правого снимков.
6.8. Точность определения координат точек объекта по измерениям стереопары
Чтобы получить формулы, по которым можно рассчитать точность определения координат точек сфотографированного объекта по измерениям стереопары, воспользуемся формулами (5.23) идеального случая аэросъёмки в системе координат SЛXYZ. Опустив индексы у координат и параллакса, запишем
Bx By Bf
X = ![]() , Y =
, Y = ![]() ,
Z =
,
Z = ![]() .
(6.20) p p p
.
(6.20) p p p
Из формул (6.20) видно, что точность вычисления плановых координат Х и Y зависит от точности измерения координат x, y и продольного параллакса p, а точность вычисления высоты Z - только от точности измерения продольного
параллакса p. С учётом этого, продифференцировав формулы (6.20), получим
![]()
![]()
![]() B Bx B By Bf dX = dx dp,
dY = dy dp,
dZ = dp. p p2 p p2 p2
B Bx B By Bf dX = dx dp,
dY = dy dp,
dZ = dp. p p2 p p2 p2
Перейдем к средним квадратическим ошибкам, учитывая следующее:
B Z H Bf 2 B f2 2
p f f , H = р = b и p = H2 . В результате получим
![]()
![]() mX Hf mx2
xb 2 mp2 , mY Hf my2
by 2 mp2 ,
mZ
mX Hf mx2
xb 2 mp2 , mY Hf my2
by 2 mp2 ,
mZ ![]() Hb
mp,
Hb
mp,
где mX, mY, mZ - средние квадратические ошибки определения координат точек объекта,
mx, my, mp - средние квадратические ошибки измерения координат и продольного параллакса на стереопаре,
b - базис фотографирования в масштабе съёмки.
Если принять, что ошибки измерений примерно равны, т.е. mx my mp, то
Hm
![]()
![]() mX x 1
x /b2 2 , mY Hmy 1
y /b2 2 , mZ Hmp .
mX x 1
x /b2 2 , mY Hmy 1
y /b2 2 , mZ Hmp .
![]()
f f b
Второй член подкоренного выражения будет иметь максимальную величину при максимальных значениях координат х и у, т.е. ошибки mX и mY будут иметь максимальную величину в углах стереопары. В этом случае х у b, и x2 y2
![]() 1.
В результате формулы расчёта точности определения координат
1.
В результате формулы расчёта точности определения координат
b2 b2
точек сфотографированного объекта по измерениям стереопары принимают вид:
![]()
![]() mX Hmx 2 , mY
Hmy 2 , mXY Hmxy 2 , mZ
mX Hmx 2 , mY
Hmy 2 , mXY Hmxy 2 , mZ ![]() Hmp , (6.21) f f f b
Hmp , (6.21) f f f b
где mXY = mX2 mY2 и mxy = mx2 my2 - средние квадратические ошибки планового положения точек на объекте и на стереопаре.
Если предположить, что:
1) снимки получены в идеальной центральной проекции,
2) построенная по ним модель объекта не имеет ошибок, вызванных ошибками взаимного ориентирования,
3) измерительный прибор не вносит своих ошибок, то mx, my и mp в формулах (6.21) будут ошибками наведения измерительной марки на точки стереопары, значения которых mx my mp 5 мкм (см. 1.6). Подставив эту величину в формулы (6.21) и приняв b = 70 мм (для формата
18х18 см и продольного перекрытия 60%), можно рассчитать ожидаемую точность определения координат точек объекта по измерениям стереопары.
H H
mX
= mY = 0,007 ![]() , mZ =
, mZ = ![]() .
(6.22) f 14000
.
(6.22) f 14000
Для формата снимков 23х23 см и продольного перекрытия 60% базис фотографирования в масштабе снимков b = 90 мм, и ожидаемая точность определения
H
высот точек
объекта будет mZ = ![]() .
.
18000
Однако полученные значения ошибок будут завышенными, т.к. не
учитывались влияния источников ошибок, описание которых дано в главе 3. В
результате у реальных снимков указанная точность будет ниже.
7. ТЕХНОЛОГИЧЕСКИЕ ПРОЦЕССЫ ПРИ СОЗДАНИИ И ОБНОВЛЕНИИ КАРТ ПО СНИМКАМ
Технологии создания и обновления топографических карт в масштабах от 1:500 и мельче основаны на использовании стереофототопографической съёмки. На рис. 7.1 приведена технологическая схема укрупнённых процессов (показаны в утолщённых рамках), входящих в этот вид съёмки при создании цифровых топографических карт, а также, какой вид продукции (показаны в тонких рамках) передаётся из одного процесса в другой. Далее даются краткие пояснения каждого процесса.
Точки государственной геодезической сети (ГГС) - пункты триангуляции, нивелирования, полигонометрии - используются как опорные точки при создании съёмочного обоснования и фотограмметрической обработке снимков.
Снимки, полученные при аэро-, наземной или космической съёмке, используются при полевом дешифрировании, создании съёмочного обоснования и при фотограмметрической обработке снимков. Если во время проведения съёмки использовалась спутниковая навигационная система или при выполнении наземной съёмки применялись наземные геодезические измерения, то полученные координаты центров проекции снимков используют при фотограмметрической обработке снимков.
Т.к. пункты ГГС располагаются довольно разреженно, их дополняют точками съёмочного обоснования (плановыми и высотными опознаками) для обеспечения опорными точками последующего фотограмметрического сгущения, выполняемого путём построения сетей фототриангуляции.
Проектирование количества и расположения опознаков производят с учётом масштаба создаваемой карты, установленной высоты сечения рельефа и точности фотограмметрического сгущения. Исходя из этих условий, сеть съёмочного обоснования может быть разреженной и сплошной. При разреженной сети расстояния между опознаками определяют, исходя из допусков, установленных для внешнего ориентирования и уравнивания сети фототриангуляции (см. 8.3 и 8.5). Если же фототриангуляция не может обеспечить требуемую точность определения координат точек сгущения, то сеть съёмочного обоснования делают сплошной, т.е. каждую стереопару обеспечивают, как минимум, четырьмя опорными точками, расположенными в углах её рабочей площади. При выполнении аэросъёмки в двух масштабах опознаками обеспечивают аэроснимки, по которым будут выполнять построение сети фототриангуляции. Определение координат опознаков выполняют после аэросъёмки.
Если технология съёмочного обоснования предполагает маркировку опознаков на местности, то этот процесс выполняют до аэросъёмки, а полевые работы по определению координат маркированных точек производят параллельно с аэросъёмкой, если последняя проводится сразу же по окончании работ по маркировке. Опыт показывает, что точность наведения измерительной марки на точки, маркированные на местности, выше, чем на не маркированные точки
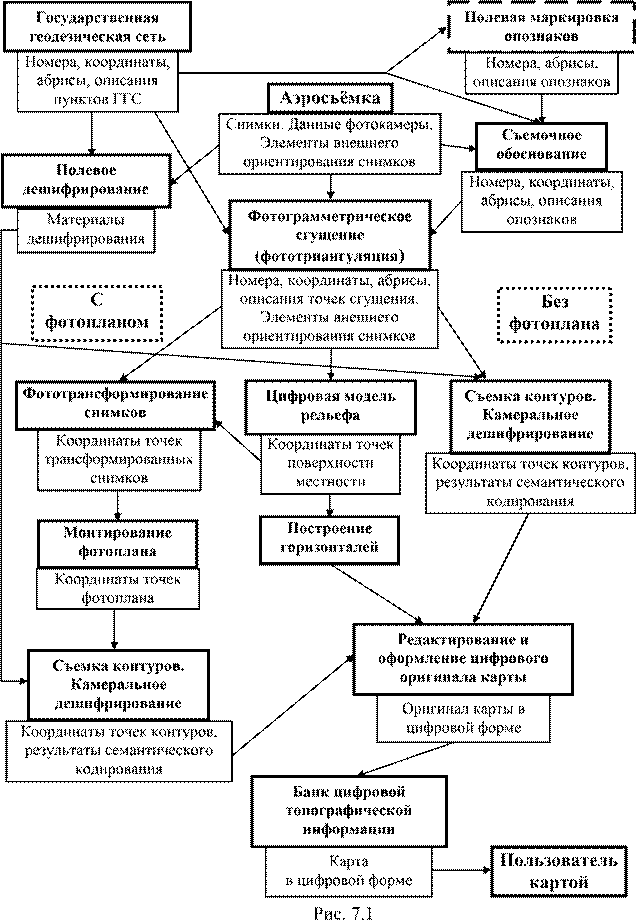
или маркированные на снимках. При этом наилучший эффект будет достигнут, если точки будут покрашены краской, дающей максимальное отражение света в той зоне спектра, для которой аберрации у объектива фотокамеры сведены до минимума. В этом случае изображение замаркированной точки будет наиболее чётким, и наведение на неё измерительной марки будет выполняться с точностью порядка 5-10 мкм.
В результате построения сетей фототриангуляции каждый снимок обеспечивают элементами внешнего ориентирования, а рабочие площади каждого снимка и каждой стереопары - опорными точками. Если во время съёмки с помощью ГЛОНАСС или GPS были определены элементы внешнего ориентирования снимков, то их используют в качестве дополнительных опорных данных.
По стереопарам выполняют построение цифровой модели рельефа, которую используют при фототрансформировании снимков и для построения горизонталей.
Съёмку рельефа выполняют либо с использованием цифровой модели рельефа, по которой в автоматическом режиме строят горизонтали, либо их прочерчивает оператор путём трассирования. Второй способ используют при съёмке равнинной местности, когда в пределах рабочей площади стереопары имеет место небольшой перепад высот и, соответственно, небольшое количество горизонталей. В этом случае прочерчивание горизонталей займёт меньше места, чем через построение ЦМР.
Съёмку контуров выполняют по фотоплану или по стереомодели местности (без фотоплана). Фотопланы изготавливают на равнинные и всхолмленные районы, а также на сельские населённые пункты с малоэтажной застройкой. Стереорисовку контуров выполняют по снимкам горных и высокогорных районов, а также городских населённых пунктов с плотной многоэтажной застройкой.
Съёмка контуров связана с дешифрированием аэроснимков, которое выполняют преимущественно камерально, но дополняют полевым дешифрированием, которое осуществляют с наземных маршрутов. В труднодоступных районах в дополнение к дешифрированию с наземных маршрутов или взамен их выполняют аэровизуальное дешифрирование с вертолёта или самолёта, пролетая над земной поверхностью на высотах 200-300 м. Сплошное полевое дешифрирование производят в крупных населённых пунктах и на участках, где много не дешифрируемых камерально топографических объектов.
После всех указанных операций выполняется редактирование и оформление цифрового оригинала карты, после чего он отправляется в банк цифровой топографической информации (БЦТИ). Цифровая карта хранится на машинном носителе в БЦТИ в масштабе 1:1, т.е. в натуральных размерах, в основном, в метрах. Её точность должна соответствовать точности наиболее крупномасштабной карты в графическом виде, которую можно создать по данным снимкам. В БЦТИ пользователь картой приобретает её в цифровой форме и собственными средствами делает тираж в нужном количестве или заказывает этот тираж.
При создании топографической карты масштаба 1:М с сечением hСЕЧ рельефа горизонталями с помощью стереофототопографической съёмки необходимо правильно рассчитать технические параметры аэросъёмки, т.к. точность создаваемой карты и её контурная нагрузка определяется точностью и дешифровочными возможностями снимков. Для расчёта технических параметров топографической аэросъёмки необходимо установить масштаб аэросъёмки 1:m, высоту фотографирования H и фокусное расстояние f фотокамеры. Значения этих параметров вначале выбирают приближенно, а затем уточняют путём подстановки в равенство H = fm.
Масштаб аэросъёмки выбирают, исходя из масштаба создаваемой топографической карты. При этом необходимо масштаб аэросъёмки выбрать как можно мельче масштаба карты. Это объясняется тем, что уменьшение масштаба аэросъёмки сокращает число снимков и, следовательно, уменьшает затраты на аэросъемочные, геодезические и камеральные фотограмметрические работы. Однако уменьшение масштаба аэросъёмки приводит к снижению точности фотограмметрических измерений и ухудшению дешифровочных возможностей снимков, поэтому в зависимости от масштаба создаваемой карты в таблице 6.1 приведены применяемые в топографической аэросъёмке значения отношений масштабов карты и снимков.
Таблица 6.1
|
1:M |
1:100000 |
1:25000 |
1:10000 |
1:5000 |
1:2000 |
1:1000 |
1:500 |
|
m
M |
0,6-1,0. 0,3 |
1,2-2,5 |
1,2-3,0 |
1,2-4,0 |
1,5-5,0 |
3,0-5,0 |
3,3-6,0 |
m
Из
приведенных величин ![]() видно, что если для
крупномасштабных
видно, что если для
крупномасштабных
M
карт аэросъёмку проводят в более мелких масштабах, то с уменьшением масштаба карты расхождение становится не столь большим, и для масштаба 1:100000 аэросъёмка производится даже в более крупном масштабе. В то же время для того, чтобы камеральное дешифрирование позволяло выявить до 75% топографических объектов, которые должны быть изображены на карте заданного масштаба, масштаб аэросъёмки не должен быть мельче 1:30000. Если при создании крупномасштабных карт эта проблема не возникает, то, например, при создании карты масштаба 1:100000 аэросъёмку выполняют двумя фотокамерами в двух масштабах. Снимки мелкого масштаба используют для фотограмметрической обработки, а снимки крупного масштаба, примерно 1:30000, - для дешифрирования. Однако в настоящее время выполнять аэросъёмку с целью создания карт в масштабах мельче 1:25000 нецелесообразно, т.к. на всю территорию страны имеется карта масштаба 1:25000 и после её обновления могут быть обновлены и созданы карты более мелких масштабов.
![]() Допустимую
высоту фотографирования рассчитывают исходя из требуемой точности измерения
высот точек по снимкам. Для этого из формулы (5.23) для координаты Z
выводят формулу для расчёта высоты съёмки. bmZ ,
(7.1)
Допустимую
высоту фотографирования рассчитывают исходя из требуемой точности измерения
высот точек по снимкам. Для этого из формулы (5.23) для координаты Z
выводят формулу для расчёта высоты съёмки. bmZ ,
(7.1)
H =
mp
где b - базис фотографирования в масштабе аэроснимков, mZ - средняя квадратическая ошибка измерения высот точек, mР - средняя квадратическая ошибка измерения продольного параллакса.
Значение mZ устанавливают исходя из требований к точности построения сети фототриангуляции (см. 8.3), заданной средней ошибкой h в виде доли высоты сечения рельефа горизонталями. При переходе к средним квадратическим ошибкам нужно учесть, что mZ = 1,25 h. После подстановки этого соотношения в (7.1) получим формулу для подсчёта предельной высоты фотографирования, выше которой при заданном значении средней ошибки h аэросъёмку производить нельзя.
![]() 1,25bh .
(7.2) Нпред. =
1,25bh .
(7.2) Нпред. =
mp В топографической аэросъёмке используют фотокамеры с фокусными расстояниями f = 70, 100 (широкоугольные), 140, 200 (нормальноугольные),
350 и 500 (узкоугольные) мм и форматом кадра 18х18 см или 23х23 см.
При выборе фокусного расстояния фотокамеры необходимо иметь в виду, что для повышения точности измерения высот точек местности следует использовать короткофокусные фотокамеры с большим форматом кадра. Однако при использовании таких фотокамер для съёмки рельефной местности разности продольных параллаксов становятся большими, что приводит к сокращению восприятия глубины стереоскопической видимости. Следовательно, короткофокусную фотокамеру нужно использовать для съёмки равнинной местности, а для съёмки рельефной, залесённой местности или городской территории с многоэтажной застройкой применять длиннофокусную фотокамеру. Если предполагается плановую часть карты создавать с использованием фотоплана, то лучше выбирать длиннофокусную или нормальнофокусную фотокамеру.
Рассчитать величину минимально допустимого значения фокусного расстояния можно, используя формулу
![]() fMIN = 1000r(Amax
Amin) .
(7.3)
fMIN = 1000r(Amax
Amin) .
(7.3)
2M r hпред
Если расчётное значение fMIN будет больше всех фокусных расстояний, используемых при топографической аэросъёмке, то фототрансформирование снимков возможно только с использованием цифровой модели местности.
Выбрав примерные значения масштаба съёмки, высоты фотографирования и фокусного расстояния, подставляют их в формулу H = fm, и, изменяя их величины, добиваются выполнения равенства. В результате будут установлены их окончательные значения, по которым выполняют расчёт основных параметров топографической аэросъёмки.
1. Исходя из значения высоты фотографирования H, рассчитывают абсолютную высоту полёта Набс. (рис. 7.2) над уровенной поверхностью по фор-

У р о в е н н а я п о в е р х н о с т ь Рис. 7.2
муле: Набс = Н + Аср,
где Аср = Amax Amin - средняя высота, вычисленная по максимальной и ми2
нимальной отметкам на участке. При этом отдельные вершины не учитывают. Затем рассчитывают высоту полёта относительно аэродрома.
Нотн = Набс - Аа,
где Аа - высота аэродрома.
2. Базис фотографирования (расстояние, которое пролетает самолёт между двумя последовательными открытиями затвора фотокамеры) вычисляют по формуле:
![]() BX = lx 1100Px Hf ,
BX = lx 1100Px Hf ,
где lx - размер стороны снимков, расположенной вдоль полёта, РX - величина продольного перекрытия.
3. Расстояние между соседними маршрутами вычисляют по формуле:
Py H
![]() BY = ly 1100 f ,
BY = ly 1100 f ,
где ly - размер стороны снимков, расположенной поперек полёта, РY - величина поперечного перекрытия.
4. Число снимков в маршруте вычисляют по формуле:
Dx + 1,
n =
Bx
где DX - размер участка вдоль маршрутов.
5. Число маршрутов вычисляют по формуле:
DY + 1,
k =
BY
где DY - размер участка поперек маршрутов.
Отношения Dx и DY округляют до целого в сторону увеличения неза-
Bx BY
висимо от величины дробной части. Один снимок и маршрут добавляют для обеспечения границ съемочного участка. При продольном перекрытии 80% или 90% добавляют 2 или 4 снимка, соответственно.
6. Общее число снимков вычисляют по формуле:
N = nk.
Исходя из этого числа, рассчитывают требуемое количество катушек фотоплёнки, разделив общее число снимков на число кадров на катушке.
7. Интервал фотографирования (временной интервал между двум последовательными открытиями затвора фотокамеры) вычисляют по формуле:
Bx ,
=
V
где BX - базис фотографирования, V - скорость самолёта.
8. Время, затрачиваемое на аэросъёмку всего участка, вычисляют по формуле:
T = N. 9. Сдвиг изображения в плоскости прикладной рамки фотокамеры во время экспонирования рассчитывают по формуле (3.12). Если расчётное значение сдвига изображения превышает 0,05 мм, то используют фотокамеру с компенсацией сдвига.
7.3. Обновление топографических карт по снимкам
С течением времени природные факторы и деятельность человека изменяют внешний вид участков земной поверхности и они перестают соответствовать содержанию топографических карт, созданных ранее на эти участки. В результате возникает необходимость либо создавать карту заново, либо обновлять существующую. Карту создают заново, если 1) земная поверхность изменила свой внешний вид существенно и на значительной площади, что требует создания новой планово-высотной основы карты; 2) изменились требования к точности карты, и ранее выполненная съёмка им не соответствует.
Однако такие изменения происходят редко. Кроме того, из двух составляющих внешнего вида земной поверхности: ситуации и рельефа, последний на больших площадях не изменяется длительное время, а возникающие из-за природных факторов и деятельности человека изменения носят локальный характер. Что касается ситуации, то её изменения носят динамичный характер. Старение карт на районы интенсивного развития государственного хозяйства происходит значительно быстрее, чем на малообжитые районы. В связи с этим обновление карт на обжитые и промышленно развитые районы выполняется через 6-8 лет, а на остальные районы - через 10-15 лет.
Обновление карт через определённые промежутки времени называется периодическим и является основным. В то же время на районы с интенсивным развитием хозяйства, где изменение ситуации происходит очень быстро, применяется непрерывное обновление карт, для чего ведут дежурную карту масштаба 1:25000 или 1:10000, на которую наносят возникающие изменения и на основе этой карты издают обновлённую. Для остальных районов в качестве дежурной карты используют карту масштаба 1:100000. Обновление дежурной карты выполняют путём постоянного дополнения её содержания по материалам исполнительных съёмок. Это достигается на основе внедрения системы картографического учёта, обеспечивающего непрерывное поступление информации об имевших место изменениях на местности. По непрерывному принципу ведут обновление морских навигационных карт.
Топографические карты масштабов от 1:5000 до 1:500 охватывают сравнительно небольшие участки местности, где хозяйственная деятельность человека распространяется на большую их площадь. В связи с этим обновление этих карт экономически невыгодно и целесообразней создавать их заново.
Обновление карт выполняют тремя способами: 1) по снимкам, 2) по картоматериалам более крупного масштаба, 3) полевыми топографическими съёмками. Полевые топографические съёмки применяют для обновления крупномасштабных карт на небольшие участки, когда нет материалов аэросъёмки или она экономически невыгодна. Обновление по картографическим материалам крупного масштаба применяется для карт мельче масштаба
1:25000.
Обновление топографических карт производят, в основном, по снимкам с использованием компьютерной техники. При обновлении используют три способа: 1) по одиночным снимкам, 2) по новому фотоплану, 3) по модели местности.
1. Обновление карты по снимкам выполняют, если объём исправлений меньше 30-40% контурной нагрузки карты, и применяют для плоскоравнинных и равнинных районов.
2. Обновление карты на основе нового фотоплана производят, если объём исправлений превышает 30-40%, и применяют для плоскоравнинных, равнинных и всхолмленных районов.
3. Обновление карты по модели местности выполняют для рельефных, горных районов.
Технологическая схема укрупнённых процессов обновления карт по снимкам приведена на рис. 7.3. Необходимо отметить, что технический проект может составляться после аэросъёмки, если она была проведена ранее. Однако со времени её выполнения не должно пройти более 1 года при обновлении карт экономически развитых районов и 3-4 года для остальных районов. При проектировании новой аэросъёмки необходимо исходить из условий, что обновляется только контурная часть карты. В связи с этим нужно выбирать более мелкий масштаб съёмки, использовать длиннофокусную фотокамеру с большим форматом кадра. Это облегчит создание фотоплана и камеральное дешифрирование.
В подготовительные работы входят: сбор материалов картографического значения, анализ объёма и характера изменений местности, составление рабочего проекта камеральных работ, преобразования топографической карты и снимков в цифровую форму и ввода их в компьютер, построение цифровой модели рельефа по оцифрованным горизонталям.
В фотограмметрическую обработку снимков входят: фотограмметриче-

ское сгущение опорной сети путём построения сетей фототриангуляции, орт офототрансформирование снимков с использованием ЦМР и монтирование фотоплана, съёмка контуров по фотоплану (равнинно-всхолмленные районы) или по стереомодели (горных районов).
После камерального исправления карты производят полевое обследование, в ходе которого уточняют объекты, дешифрированные неуверенно, и производят съёмку объектов, не изобразившихся на снимках или появившихся после проведения аэросъёмки. Кроме того, производят сбор сведений для топографического описания и уточняют названия объектов.
По завершении указанных работ изготавливают издательский оригинал и приступают к обновлению карт всего масштабного ряда вплоть до 1:100000, включительно, что должно быть сделано за период, не превышающий 2-3 года.
В последние годы для обновления карт в масштабах 1:50000 и мельче используют космические снимки. Преимущество этих снимков перед аэроснимками состоит в том, что фотосъёмку из космоса производят в масштабах примерно соответствующих масштабам обновляемых карт. В результате изображения контуров земной поверхности получаются на космических снимках в естественной генерализации. Кроме того, использование космических снимков для создания и обновления карт снижает экономические затраты за счёт снижения числа снимков, поступающих на фотограмметрическую обработку. Для повышения качества дешифрирования космических снимков экономически развитых районов фотосъёмку производят длиннофокусными фотокамерами. Технологическая схема обновления топографических карт по космическим снимкам остается практически такой же, что и при обновлении по аэроснимкам. Отличие заключается в методиках выполнения отдельных процессов фотограмметрической обработки космических снимков по сравнению с обработкой аэроснимков. Необходимо отметить, что по космическим снимкам, прежде всего, обновляют контурную нагрузку карты. Что касается высотной нагрузки, то точность стереоскопических измерений высот точек земной поверхности по космическим снимкам позволяет вычерчивать горизонтали только с большими сечениями, которые используют на мелкомасштабных картах высокогорных районов.
7.4. Фотосхема
В настоящее время в связи с тем, что территория страны покрыта топографическими картами от масштаба 1:25000 и мельче, фотосхема потеряла своё былое значение. Однако в отдельных случаях, когда имеется только фотосъёмочный материал, а карт нет под рукой, она может сыграть свою роль, как и прежде. При фотосъёмке поверхностей других космических тел фотосхема также может сыграть свою роль. Всё это вытекает из её достоинства, заключающегося в скорости изготовления.
Для создания карты по снимкам нужно выполнить достаточно большой объём работ, который требует затрат большого количества времени. После получения снимков готовая карта может появиться через 1,5-2 года. Однако сразу же после получения фотоотпечатков с негативов или же после ввода в компьютер снимков в цифровой форме можно смонтировать фотосхему.
Фотосхема, являясь предварительным картоматериалом, позволяет в короткие сроки получить информацию о сфотографированной местности в единой связности, произвести предварительное топографическое и специальное дешифрирование. Она может быть использована при рекогносцировке и составлении проекта топографо-геодезических и инженерно-технических работ.
Фотосхемы бывают одно- и многомаршрутные в зависимости от того, из какого числа маршрутов они смонтированы. Фотосхемы монтируют из рабочих площадей снимков, соединённых в одно целое по общим контурам. Для монтирования можно использовать два способа: по контурам и по начальным направлениям. Начальным направлением является линия, прочерченная на аэроснимке через контур, расположенный в центре снимка, и контур, расположенный на краю снимка и опознанный в центре соседнего снимка. Способ по начальным направлениям более точный, но требует больших затрат времени. Кроме того, на компьютере его использование затруднено. Способ по контурам позволяет быстрее смонтировать фотосхему. Т.к. преимущество фотосхемы в скорости изготовления и она не относится к измерительным картографическим документам, то способ монтирования по контурам является основным.
На компьютерах для соединения цифровых снимков разработаны программы, которые автоматически выбирают линии разреза.
При монтировании фотосхем из снимков равнинной местности, особенно, если снимки получены при гиростабилизации, больших трудностей в совмещении одинаковых контуров не возникает. Смонтировать фотосхему из снимков рельефной местности гораздо труднее, т.к. из-за влияния рельефа на линии разреза одинаковые контура могут исчезнуть или удвоиться. К этим трудностям добавляются расхождения контуров из-за разномасштабности снимков, вызванной разными высотами фотографирования. С целью равномерного распределения ошибок монтирования по площади фотосхемы работу начинают со среднего аэроснимка среднего маршрута.
Если смонтировать отдельно нечётные и чётные снимки, то будут получены две маршрутные фотосхемы, которые составят вместе стереоскопическую фотосхему. При рассматривании такой фотосхемы под специальным стереоскопом удобно, например, проектировать линейные объекты: дороги, трубопроводы, линии электропередач.
Для определения точности монтирования фотосхемы производят оценку расхождений контуров вдоль разрезов. По полученным расхождениям рассчитывают среднюю квадратическую ошибку монтирования фотосхемы по
2
![]() формуле m = ,
где n - число использованных контуров. На фотосхеме, 2n
формуле m = ,
где n - число использованных контуров. На фотосхеме, 2n
смонтированной из топографических снимков, m 1 мм при предельной величине расхождений контуров, равной 2 мм.
Масштаб фотосхемы определяют разными способами в зависимости от её назначения, характера местности, количества маршрутов. Для фотосхем, изготовленных из снимков плоской или равнинной местности, берут значение масштаба, равного масштабу аэросъёмки. В остальных случаях масштаб фотосхемы определяют по опознанным на ней точкам с известными координатами, или по контурам, опознанным на топографической карте и фотосхеме.
8. ФОТОТРИАНГУЛЯЦИЯ
8.1. Назначение и классификация фототриангуляции
До появления ЦФС фототриангуляция служила для определения координат опорных точек, которые использовались при фотограмметрической обработке каждого снимка и каждой стереопары. После появления ЦФС фототриангуляцию используют для определения элементов внешнего ориентирования каждого снимка, которые задают ориентацию систем координат снимков в системе координат объекта и тем самым обеспечивают выполнение последующих процессов обработки снимков.
В зависимости от числа аэросъёмочных маршрутов, используемых при построении сетей фототриангуляции, она подразделяется на маршрутную (одномаршрутную) и блочную (многомаршрутную). Последняя строится по двум и более маршрутам. Блочная фототриангуляция имеет преимущество перед маршрутной, т.к. для её внешнего ориентирования общее число опорных точек и их густота расположения будут меньше, чем при построении на ту же площадь маршрутных сетей.
Для построения сетей фототриангуляции стандартное продольное перекрытие снимков должно составлять не менее 60%, а поперечное - не менее 30%. В отдельных случаях для повышения точности построения блочных сетей съёмку выполняют при перекрытиях 60% как в продольном, так и в поперечном направлениях. Иногда перпендикулярно к основным маршрутам прокладывают аэросъёмочные каркасные маршруты, накрывая ими начало и конец основных маршрутов. Это позволяет сократить затраты на полевые определения опорных точек. В каркасных маршрутах продольное перекрытие устанавливают 80%, что обеспечивает как бы прокладку двух маршрутов с 60%-м перекрытием, если брать снимки через один. Построение независимо двух маршрутных сетей по одним и тем же точкам обеспечивает повышение точности определения координат точек.
Для построения сетей фототриангуляции используют два способа: независимых моделей и связок. Независимые модели строят по отдельным стереопарам, а затем по связующим точкам их соединяют в общую модель. В результате получают свободную сеть, т.е. сеть в масштабе, близком к заданному, и с примерной ориентировкой в системе координат объекта. Затем выполняют внешнее ориентирование и уравнивание свободной сети по опорным точкам. Способ связок позволяет построить, ориентировать и уравнять сеть одновременно по всем снимкам без построения моделей.
8.2. Точки, включаемые в сеть фототриангуляции
Составление рабочего проекта сети фототриангуляции подразумевает выбор точек, подлежащих включению в сеть. При этом нужно соблюдать следующие условия:
- точки следует выбирать на плоских участках, совмещая их с надёжно отождествляемыми контурами. Нельзя выбирать точки рядом с вертикальными объектами, на крутых скатах, затенённых участках оврагов и лощин;
- точка должна располагаться на большем числе соседних снимков;
- расстояния между соседними точками должно быть более 1 мм;
- точки должны быть удалены от края снимка на 10-15 мм;
- номер точки не должен повторяться у другой точки;
- точки следует выбирать при стереоскопическом рассматривании снимков с увеличением 8-12 крат;
Выбор точек производят либо на контактных отпечатках, либо непосредственно на диапозитивах, либо на экране монитора при работе на ЦФС. Точки сети накалывают на контактных отпечатках чётных снимков. С обратной стороны вокруг накола рисуют абрис и подписывают рядом номер. При работе на ЦФС создают фотоабрисы.
В сеть фототриангуляции включают следующие группы точек.
1. Опорные точки (рис. 8.1), в качестве которых используют пункты
|
|
|
|
|
|
|
|
|
|
![]() Рис. 8.1
Рис. 8.1
триангуляции, полигонометрии, нивелирные реперы, точки съёмочного обоснования - опознаки. Если использовались каркасные маршруты, то опорные точки выбирают из сети фототриангуляции, построенной по этим маршрутам. Опорные точки должны быть определены со средней ошибкой в плане, не превышающей 0,1 мм в масштабе создаваемой карты, а по высоте, не превышающей 0,1 принятой высоты сечения рельефа.
Каждый маршрут должен иметь следующий минимум опорных точек: на первой стереопаре - две планово-высотные точки, а на последней - одну планово-высотную точку. Однако с целью исключения влияния систематических ошибок берут избыточное число опорных точек: на первой и последней стереопарах - по две планово-высотные точки (на рис. 8.1, а обозначены треугольником) и в середине - одну-две высотные точки (обозначены квадратом). Лучше, если опорные точки будут расположены в углах рабочих площадей стереопар (см. рис. 1.4), что позволит заменить ими остальные точки сети и тем самым сократить их общее число. В блочных сетях (на рис. 8.1, б изображен блок из 3-х маршрутов) опорные точки размещают по периметру в межмаршрутных перекрытиях вертикальными рядами с различной частотой, определяемой масштабом создаваемой карты и высотой сечения рельефа.
2. Точки взаимного ориентирования (рис. 8.2, а), предназначенные для построения модели местности, располагают в углах рабочей площади стереопары и в районах главных точек снимков. Это, так называемое, стандартное расположение. Точки намечают по две-три рядом. Таким образом, точек взаимного
|
|
|
|
|
Рис. 8.2
ориентирования бывает 12-18.
|
|
|
|
|
|
3. Межмодельные связующие точки (рис. 8.2, б), используемые для соединения моделей, располагают в зоне тройного перекрытия - перекрытия двух соседних стереопар. Их должно быть не меньше трёх: одна - в районе главной точки среднего снимка и две другие - внизу и вверху зоны на расстоянии 2 см от края снимка. Для повышения точности соединения моделей связующие точки намечают рядом по две-три. При этом их смещают относительно друг друга влево и вправо на ширину зоны тройного перекрытия, что позволяет ослабить "шарнирный эффект" между моделями (их взаимный продольный наклон). 4. Межмаршрутные связующие точки (рис. 8.3), используемые для связи маршрутов, намечают в зоне поперечного перекрытия. В качестве этих точек используются межмодельные связующие точки, расположенные вверху и внизу зоны тройного продольного перекрытия. С каждой стереопары переносят две-три точки, которые расположены на чётких контурах. С целью снижения влияния "шарнирного эффекта" Рис. 8.3 между маршрутами (взаимного попе-
речного наклона) эти точки необходимо располагать по ширине перекрытия. Точки располагают равномерно по ширине и длине поперечного перекрытия.
5. Характерные точки рельефа и точки на урезах воды, отметки которых подписывают на карте, намечают равномерно по площади стереопары. Точки на урезах воды намечают через 10 см в масштабе карты. С целью повышения точности построения профилей водотоков, их намечают в два раза чаще. 6. Контрольные точки намечают не менее трёх на стереопару. Они будут использованы для контроля процессов составления оригинала карты и трансформирования снимков.
С целью сокращения числа точек в сети следует совмещать точки, расположенные в одних местах стереопары. Общее число точек на стереопаре должно быть не более 20-30.
Рабочий проект оформляется в виде схемы, на которую наносят выбранные точки и их номера, а также центры снимков с их номерами.
8.3. Принцип построения сети фототриангуляции способом независимых моделей
Процесс построения сети фототриангуляции способом независимых моделей состоит из построения свободной сети и её ориентирования в геодезической системе координат.
Построение свободной сети заключается в том, что вначале по стереопарам строят не связанные друг с другом модели в их собственных системах координат и масштабах (см. 6.3 и 6.4). Затем построенные модели соединяют в единую модель. Принцип соединения следующий. На рис. 8.4 схематично изо-
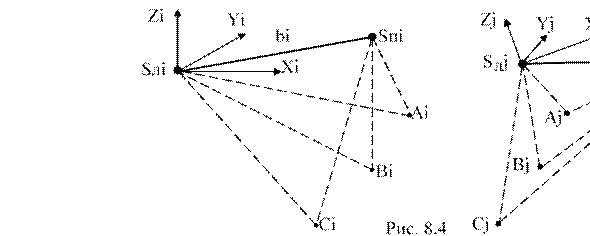
бражены две соседние в маршруте модели: i-я и j-я. Каждая модель построена в своей системе координат: левая - в системе координат SЛiXiYiZi, правая - в системе координат SЛjXjYjZjj. Начала систем координат каждой модели расположены в левом центре проекции. Масштабы моделей заданы величинами базисов проектирования bi и bj.
Чтобы соединить две модели и привести их к единому масштабу используют расположенные в зоне перекрытия моделей (зоне тройного перекрытия снимков) межмодельные связующие точки Ai, Bi, Ci на i-й модели и соответствующие им точки Aj, Bj, Cj на j-й модели. Кроме этих точек используют в качестве связующей точки центр проекции среднего снимка, который на i-й модели обозначен SПi, а на j-й модели - SЛj. Четыре указанные точки позволяют определить взаимную ориентацию моделей и масштабный коэффициент, являющийся отношением масштабов моделей.
Для соединения моделей, расположенных в соседних маршрутах ис-
![]() Xj пользуют
межмаршрутные связующие точки (на рис. 8.5 точки K, M и N). Ни один центр
проекции в этом процессе не участвует. В связи с этим соединение моделей в
поперечном направлении выполняется менее жёстко.
Xj пользуют
межмаршрутные связующие точки (на рис. 8.5 точки K, M и N). Ни один центр
проекции в этом процессе не участвует. В связи с этим соединение моделей в
поперечном направлении выполняется менее жёстко.
Соединение моделей как в продольном, так в поперечном направлениях происходит одновременно. Математическое решение задачи представляет собой преобразование координат из одной пространственной системы координат в другую с одновременным приведением их к единому масштабу. С учётом этого уравнения соединения моделей имеют вид:
X'Y'Z'iii Y'X'Z'SSSпiпiпi A ' ' ' Y'X'Z'jjjt', (8.1)
где X'i, Y'i, Z'i - координаты точек i-й модели в системе координат SЛiXiYiZi,
X'j, Y'j, Z'j - координаты точек j-й модели в системе координат SЛjXjYjZj,
X'SПi, Y'SПi, Z'SПi - координаты правого центра проекции i-й модели в системе координат SiЛXiYiZi,
', ', '- угловые элементы ориентирования системы координат SЛjXjYjZj относительно системы координат SЛiXiYiZi,
t' - масштабный коэффициент.
В уравнениях (8.1) величины X'SПi, Y'SПi, Z'SПi, ', ', ', t' являются элементами взаимного ориентирования моделей. Координаты X'SПi, Y'SПi, Z'SПi вычисляют при построении i-й модели и их значения в следующей модели берут в качестве исходных, а при соединении моделей только уточняют. В качестве исходных значений угловых величин ', ', ' берут нули. Для масштабного коэффициента t' исходную величину рассчитывают по расстояниям между связующими точками.
Соединение моделей выполняется в два этапа. На первом этапе по разностям координат связующих точек в соседних моделях вычисляют вероятнейшие значения элементов взаимного ориентирования моделей. Т.к. уравнения (8.1) являются нелинейными относительно неизвестных, их приводят к линейному виду, беря частные производные по каждому из неизвестных. Неизвестными становятся поправки к приближённым значениям искомых величин.
![]()
![]()
![]() X'i X' X'i X'
X'i X' X'i X'
![]() X'Sпi Sпi '
' 'i 'X''i 'Xt''i t'X'jX'i vx
X'Sпi Sпi '
' 'i 'X''i 'Xt''i t'X'jX'i vx
![]()
![]()
![]()
![]() YY'
'i Y'Sпi Y''i 'Y''i 'Y''i 'Yt''i t'Y'jY'i vy, (8.2) Sпi
YY'
'i Y'Sпi Y''i 'Y''i 'Y''i 'Yt''i t'Y'jY'i vy, (8.2) Sпi
![]()
![]()
![]() Z'i Z' Z'i Z'
Z'i Z' Z'i Z'
![]() Z'Sпi Sпi '
' i' 'Z'i' 'Zt''i t'Z'jZ'i vz
Z'Sпi Sпi '
' i' 'Z'i' 'Zt''i t'Z'jZ'i vz
где X'SПi, Y'SПi, Z'SПi, ', ', ', t' - поправки к приближённым значениям элементов взаимного ориентирования моделей, а коэффициенты, стоящие перед ними, - частные производные; X'j, Y'j, Z'j, X'i, Y'i, Z'i - координаты связующих точек в соседних моделях.
По уравнениям поправок (8.2) составляют нормальные уравнения и решают их под условием [vv] = min. Вычислив величины поправок, рассчитывают новые значения элементов взаимного ориентирования моделей, которые используют для расчёта коэффициентов в уравнениях (8.2). После этого решение системы повторяют. С увеличением числа итераций разности координат Xi-Xj, Yi-Yj, Zi-Zj связующих точек будут уменьшаться. После того как они станут меньше установленного допуска, вычисления прекращают.
На межмодельных связующих точках средние квадратические расхождения плановых координат, измеренных на соседних стереопарах и приведённых в систему координат среднего, общего снимка, не должны превышать 15 мкм. Средние квадратические расхождения высот этих точек не должны превышать 15 мкм, умноженных на отношение фокусного расстояния фотокамеры к базису фотографирования в масштабе снимков.
f
z 15 ![]() .
.
b
Базис фотографирования в масштабе снимка можно рассчитать по формуле b = lX1 Px ,
100
где lX - длина кадра вдоль полёта, РХ - процент продольного перекрытия.
На межмаршрутных связующих точках средние расхождения плановых координат не должны превышать 40 мкм в масштабе сети, а средние расхождения высот этих точек не должны превышать 40 мкм, умноженных на отношение фокусного расстояния фотокамеры к базису фотографирования в масштабе снимков.
На втором этапе, используя вероятнейшие значения элементов взаимного ориентирования моделей, по формулам (8.1) рассчитывают координаты точек j-й модели в системе координат i-й. В результате последовательных соединений моделей получают координаты точек свободной сети в системе координат исходной модели и в её масштабе.
Построенную свободную сеть фототриангуляции ориентируют в геодезической системе координат, используя опорные точки, и одновременно устраняют деформации, возникшие в ходе построения сети. Методику внешнего ориентирования сети фототриангуляции можно разделить на два варианта:
1) сеть строится на небольшую площадь и сферичность Земли можно не учитывать. В этом случае внешнее ориентирование сети выполняют в координатной системе проекции Гаусса-Крюгера, принятой в нашей стране для создания топографических карт;
2) сеть строится на большую площадь и необходимо учитывать сферичность Земли. В этом случае в качестве внешней системы координат берут геоцентрическую систему координат OЦXЦYЦZЦ.
С математической точки зрения внешнее ориентирование сети фототриангуляции представляет собой преобразование координат из пространственной системы координат свободной сети в геодезическую систему координат. В ходе этого преобразования определяется и учитывается масштаб сети и её угловая ориентация. Преобразование координат выполняется с помощью следующих уравнений.
Xг XSг Xc
Yг YSг A c c c Yc tc, (8.3)
Zг ZSг Zc
где XГ, YГ, ZГ - координаты точек сети в геодезической системе координат;
XSГ, YSГ, ZSГ - координаты начала системы координат свободной сети в геодезической системе координат;
C, C, C - угловые элементы ориентирования системы координат сети в геодезической системе координат; tC - масштабный коэффициент.
XSГ, YSГ, ZSГ, C, C, C, tC - элементы внешнего ориентирования свободной сети и для их определения нужно иметь минимум три опорные точки. Наличие большего числа опорных точек позволяет решить задачу по методу наименьших квадратов. Решение уравнений производят так же, как описано соединение моделей. Составляют уравнения поправок, а т.к. уравнения (8.3) являются нелинейными относительно неизвестных, их приводят к линейному виду, беря частные производные по каждому из неизвестных. Неизвестными становятся поправки к приближённым значениям искомых величин.
![]()
![]()
![]()
![]()
![]() XXг XSг Xг с Xг
с Xг с Xt г
tс X'г Xг
vx
XXг XSг Xг с Xг
с Xг с Xt г
tс X'г Xг
vx
Sг с с с с
![]()
![]() Yг Y Y
Yг Y Y
![]()
![]()
![]() YSг Sг гс с Yгс с Yсг с Ytсг
tс Y'г Yг
vy
YSг Sг гс с Yгс с Yсг с Ytсг
tс Y'г Yг
vy
![]()
![]()
![]()
![]() Zг ZS Zг
Zг Z
Zг ZS Zг
Zг Z
![]() ZSг г с с с
с сг с Ztсг
tс Z'г Zг
vz
ZSг г с с с
с сг с Ztсг
tс Z'г Zг
vz
По уравнениям поправок составляют нормальные уравнения, из решения которых находят поправки и рассчитывают новые значения приближённых значений элементов внешнего ориентирования сети. После этого решение системы повторяют. С увеличением числа итераций разности координат X'г-Xг, Y'г-Yг, Z'г-Zг на опорных точках будут уменьшаться. Степень завершения вычислений оценивается по величинам остаточных расхождений координат на опорных и контрольных точках.
Внешнее ориентирование и уравнивание сети считается законченным, если средние остаточные расхождения не превышают:
- на опорных точках и центрах проекции снимков в плане 0,2 мм в масштабе карты, а по высоте 0,15 высоты сечения рельефа;
- на контрольных точках в плане 0,3 мм в масштабе карты, а по высоте значений долей высоты сечения рельефа, указанных в табл. 8.1.
Таблица 8.1
|
Высота сечения, м |
0,5 |
1 |
2 |
2,5 |
5 |
10 |
|
|
Доля сечения |
0,2 масштаб карты 1:500, 1:1000 |
0,25 масштаб карты 1:2000, 1:5000 |
0,2 |
0,25 |
0,25 |
0,35 |
0,35 |
При этом в открытых районах удвоенные средние расхождения должны находиться в пределах 5% от общего количества соответствующих точек, а в залесённых - в пределах 10%.
Вычисленные вероятнейшие значения элементов внешнего ориентирования сети подставляют в уравнения (8.3) и выполняют пересчёт координат точек сети из системы координат сети в геодезическую (геоцентрическую) систему координат.
Если координаты опорных точек имеют пониженную точность, например они были сняты с карты мелкого масштаба, то для распределения остаточных расхождений по полю сети можно использовать полиномы вида:
XГ = X'Г + A1 + A2X' + A3Y' + A4X'Y' + A5X'2 + A6X'3,
YГ = Y'Г + B1 + B2X' + B3Y' + B4X'Y' + B5X'2 + B6X'3,
ZГ = Z'Г + C1 + C2X' + C3Y' + C4X'Y' + C5X'2 + C6X'3,
где X'Г, Y'Г, Z'Г - вычисленные координаты точек сети в геодезической системе координат. Для определения значений коэффициентов А, В и С полиномов составляют уравнения поправок
A1 + A2X' + A3Y' + A4X'Y' + A5X'2 + A6X'3 + X'Г - XГ = Vx, B1 + B2X' + B3Y' + B4X'Y' + B5X'2 + B6X'3 + Y'Г - YГ = Vy, C1 + C2X' + C3Y' + C4X'Y' + C5X'2 + C6X'3 + Z'Г - ZГ = Vz.
Используя в качестве свободных членов остаточные расхождения координат X'Г - XГ, Y'Г - YГ и Z'Г - ZГ на опорных точках, решают систему уравнений и находят значения коэффициентов. После этого перевычисляют координаты точек сети, подставив значения коэффициентов в полиномы. Нужно отметить, что полиномы нарушают (разрывают) фотограмметрические связи и при наличии надёжных опорных точек их нельзя использовать.
По завершении построения, внешнего ориентирования и уравнивания сети фототриангуляции составляют каталог координат точек сети и элементов внешнего ориентирования снимков. Каталог дополняется фотоабрисами точек.
8.4. Построение, внешнее ориентирование и уравнивание сети фототриангуляции способом связок
Особенность построения сети фототриангуляции способом связок состоит в том, что построение моделей по стереопарам не выполняется, а построение, внешнее ориентирование и уравнивание сети фототриангуляции производится одновременно по всем снимкам. При этом учитывается, на каком количестве снимков изобразилась точка местности. Например, точка местности при продольном перекрытии более 50% может изобразиться на двух или трёх снимках одного маршрута. На рис. 8.6, а показаны три последовательных снимка S1, S2, S3 одного маршрута, на которых точка М местности изобразилась в зоне тройного продольного перекрытия (на среднем снимке зона ограничена пунктирными линиями). Следовательно, точке М соответствует три изображения: m1, m2, m3. У точек местности, не попавших в зону тройного перекрытия, будут только два изображения на одной паре снимков S1-S2 или S2-S3.
При двухмаршрутной аэросъёмке с поперечным перекрытием менее 50%
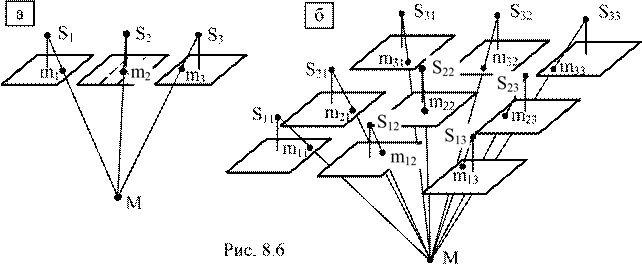
точка местности изобразится либо на четырех снимках двух маршрутов, либо на шести снимках при совпадении зон тройных продольных перекрытий из двух маршрутов. Если выполнить трёхмаршрутную аэросъёмку с продольным и поперечным перекрытиями, равными 60%, то точка местности изобразится либо на шести снимках трёх маршрутов, либо при совпадении зон тройных продольных перекрытий из трёх маршрутов на девяти снимках (рис. 8.6, б).
В основу математического решения задачи положено условие коллинеарности (5.33), определяющее связь между координатами точек местности и их изображений на наклонном снимке. Для каждого изображения точки местности на снимке можно составить два уравнения коллинеарности. Если обозначить номер точки через i, а номер снимка через n, то уравнения будут иметь вид
xin xo f cc1311nn((XXii XXSnSn))cc2321nn((YYii YYSnSn)) cc3133nn((ZZii ZZSnSn)) (8.4)
yin yo f cc1213nn((XXii XXSnSn)) cc2223nn((YYii YYSnSn))cc3332nn((ZZii ZZSnSn))
Следовательно, с учётом вышесказанного для точек, расположенных на разных участках снимка, можно составить четыре, шесть, двенадцать или восемнадцать уравнений (8.4). Минимальное число уравнений (четыре) можно составить для точки местности, изобразившейся только в зоне продольного перекрытия двух снимков. Точка, расположенная в зоне совпадения тройных продольного и поперечного перекрытий трёх маршрутов, позволяет составить максимальное количество (восемнадцать) уравнений.
В уравнениях (8.4) содержится девять неизвестных: шесть элементов внешнего ориентирования снимка XSn, YSn, ZSn, n, n, n и три координаты точки местности Xi, Yi, Zi, в системе координат объекта. При этом предполагается, что элементы внутреннего ориентирования xo, yo, f известны с достаточной точностью. Если уравнения составлены для опорной точки, у которой координаты Xi, Yi, Zi известны, то искомыми величинами будут только шесть элементов внешнего ориентирования снимка.
Однако если составить систему из уравнений (8.4) для всех точек местно-
сти и их изображений на всех снимках, то в ней не будет общих неизвестных для всех уравнений. При переходе от одной точки местности к другой и от одного снимка к другому значения неизвестных будут изменяться.
Систему уравнений (8.4) решают следующим образом. Т.к. эти уравнения нелинейны относительно неизвестных, их преобразуют в уравнения поправок, у которых в каждом члене будет только одно неизвестное.
a1XSn a2YSn a3ZSn a4 n a5 n a6 n
b1XSn ab72XYiSn a8bY3iZSna9Zbi4 x'nin bx5 in n vxb6 n (8.5)
b7 Xi b8Yi b9Zi y'in yin vy
В уравнениях (8.5) коэффициенты ai и bi, являющиеся частными производными уравнений (8.4) по каждому неизвестному, стоят перед искомыми величинами - поправками к приближённым значениям неизвестных в уравнениях (8.4). Приближённые значения задают исходя из условий съёмки и по карте. Числовые значения коэффициентов ai и bi рассчитывают по приближённым значениям неизвестных, которые используют также для вычисления по уравнениям (8.4) координат x'in и y'in. Величины координат xin и yin получают в ходе измерения снимков. Расхождения x'in - xin и y'in - yin являются свободными членами уравнений. Для определения необходимого количества уравнений в зависимости от числа неизвестных используют формулы, приведенные в табл. 8.2.
Таблица 8.2
|
Вариант |
1 |
2 |
3 |
|
Определяемые точки |
n(2r +1) |
n(r + 1) |
n(r + 2) |
|
Неизвестные |
3n(4r + 1) |
3n(3r + 1) |
3n(3r + 2) |
|
Уравнения поправок |
6r(3n - 2) + 2k |
4r(3n - 2) + 2k |
6r(3n - 2) + 2k |
В этих формулах n - число снимков в маршруте, r - число маршрутов, k - число изображений опорных точек. Формулы даны для трёх вариантов построения сети:
1) поперечное перекрытие меньше 50% и на каждой стереопаре измерены 6 стандартно расположенных точек;
2) поперечное перекрытие меньше 50% и на каждой стереопаре измерены
4 точки (по одной в каждом углу стереопары);
3) поперечное перекрытие больше 50% и на каждой стереопаре измерены 6 точек (по точке в районах главных точек 6 снимков 3-х маршрутов).
В третьем варианте количество точек сети примерно в 1,7-1,8 раза меньше, что сокращает затраты времени на измерения и вычисления.
Решение системы уравнений (8.5) проводят по методу наименьших квадратов. От уравнений поправок переходят к нормальным уравнениям, в результате решения которых получают значения поправок к приближённым значениям неизвестных. Прибавив поправки к этим значениям, находят новые значения неизвестных и, используя их в качестве приближённых значений, повторяют решение, начиная с составления уравнений поправок. Процесс повторяется до достижения требуемой точности построения сети.
Построение сети фототриангуляции способом связок позволяет наиболее эффективно использовать значения элементов внешнего ориентирования снимков, полученные в полёте с помощью спутниковых навигационных систем. Если они получены с достаточной точностью, то их используют как точные данные наравне с координатами опорных точек. Если точность их определения недостаточна, то они используются как приближённые значения неизвестных.
8.5. Точность фототриангуляции и расчёт съёмочного обоснования
В ходе построения сети фототриангуляции происходит накопление ошибок измерений от модели к модели. Как известно, ошибки измерений содержат случайную и систематическую части. Случайные ошибки, меняющие свой знак и величину, нельзя исключить из измерений, а только можно ослабить их влияние, повышая точность и число измерений. Большую часть систематических ошибок, имеющих определённую величину и знак, можно исключить, а влияние оставшейся части свести к минимуму при использовании опорных точек.
Накопление ошибок в маршрутной сети фототриангуляции происходит следующим образом. Если на первой модели точка была измерена с ошибкой 1, то она будет передаваться на все последующие модели и вызовет в измерениях точек последней n-й модели ошибку n1. Ошибка 2, допущенная на второй модели, вызовет в измерениях точек n-й модели ошибку (n-1)2. Точно также будут передаваться ошибки, допущенные на последующих моделях. Если предположить, что знаки и величины ошибок на каждой модели носят случайный характер, то ошибка в измерениях точек n-й модели будет представлять собой сумму ошибок, допущенных на предыдущих моделях, т.е.
2 = n212 + (n-1)222 + ... + 22n-12 + n2. Если принять 1 = 2 = ... = n = m1, то формула для расчёта средней квадратической ошибки на n-й модели будет иметь вид:
![]() mn
= m1 n2(n 1)2 ... 22 1.
(8.6)
mn
= m1 n2(n 1)2 ... 22 1.
(8.6)
Под корнем расположен степенной ряд из квадратов последовательных целых чисел. Его сумма может быть рассчитана по формуле
![]() n 2 (n
1)2 ... 22
1]
= 2n3 3n2
n .
n 2 (n
1)2 ... 22
1]
= 2n3 3n2
n .
[n
n1 6
С учётом этого формулу (8.6) можно записать в виде:
mn = m1  .
(8.7)
.
(8.7)
![]()
![]() После внешнего
ориентирования маршрутной сети по опорным точкам, расположенным на первой и
последней моделях, наибольшие ошибки будут на средней модели. Чтобы получить
формулу для их расчёта, в формуле (8.7) заменим n на n/2 и разделим полученное
выражение на 2 . Это объясняется тем, что определение координат точек средней
модели происходит как бы дважды из двух сетей, проложенных к средней модели от
опорных точек, расположенных на первой и последней моделях. Таким образом, вес
координат точек средней модели увеличивается в два раза и их ошибки уменьшаются
в 2 . В результате формула (8.7) примет вид:
После внешнего
ориентирования маршрутной сети по опорным точкам, расположенным на первой и
последней моделях, наибольшие ошибки будут на средней модели. Чтобы получить
формулу для их расчёта, в формуле (8.7) заменим n на n/2 и разделим полученное
выражение на 2 . Это объясняется тем, что определение координат точек средней
модели происходит как бы дважды из двух сетей, проложенных к средней модели от
опорных точек, расположенных на первой и последней моделях. Таким образом, вес
координат точек средней модели увеличивается в два раза и их ошибки уменьшаются
в 2 . В результате формула (8.7) примет вид:
![]()
![]() mС = m1 n3 3n2
2n 3 3n2
2n . (8.8) = 0,144m1 n
mС = m1 n3 3n2
2n 3 3n2
2n . (8.8) = 0,144m1 n
48
Подставим в (8.8) вместо m1 формулы (6.21) средних квадратических ошибок измерения точек одиночной модели. Получим следующие формулы расчёта ошибок в плановых положениях и высотах точек, находящихся в середине сети фототриангуляции:
![]() Hmf xy 3 3nxy2
2nxy .
(8.9) mXY 0,2 nxy
Hmf xy 3 3nxy2
2nxy .
(8.9) mXY 0,2 nxy
mZ 0,14Hmb p nz3 3nz2 2nz
Однако при создании топографических карт, когда конечная точность фототриангуляции определена инструкциями, формулы (8.9) используют на этапе создания съёмочного обоснования, когда необходимо рассчитать расстояния L nbH
между опознаками по формуле L = ![]() ,
где n это nxy или nz. Для расчёта знаf
,
где n это nxy или nz. Для расчёта знаf
чений nxy и nz формулы (8.9) можно упростить, оставив в подкоренном выражении только член третьей степени. Хотя это и приводит к снижению точности работы формул, но при расчёте числа базисов не повлияет существенно на конечный результат, т.к. расчёт nxy и nz выполняют до целых чисел с округлением в сторону увеличения. После упрощения формул (8.9) и преобразования их относительно nxy и nz получим следующие формулы:
2 2
![]()
![]() nxy 3
0,2HmfmXYxy
, nz 3 0,14HmbmZ p
, (8.10)
nxy 3
0,2HmfmXYxy
, nz 3 0,14HmbmZ p
, (8.10)
где mXY и mZ задаются инструкцией (раздел "фотограмметрическое сгущение опорной сети"), mxy и mp - точности измерения планового положения точек на стереопаре и их продольных параллаксов.
9. ПОЛУЧЕНИЕ ЦИФРОВОЙ И ГРАФИЧЕСКОЙ
ИНФОРМАЦИИ ОБ ОБЪЕКТЕ ПО СНИМКАМ
9.1. Технологическая схема фотограмметрической обработки стереопары
Если на ЦФС предусмотрен весь комплекс работ по обработке снимков, то после построения фототриангуляции для каждого снимка получают элементы ориентирования. В этом случае ориентирование стереопар не выполняют, а сразу приступают к съёмке рельефа и контуров (см. рис. 7.1). Если обрабатываются отдельные стереопары, то выполняют полную обработку согласно той программе, которая установлена в компьютере.
На разных ЦФС и АФП программы обработки снимков варьируются и, соответственно, имеются свои особенности построения и ориентирования модели, съёмки рельефа и контуров. Однако, в целом, работа выполняется одинаково, и далее даётся обобщённое описание порядка работы. На рис. 9.1 приведена технологическая схема из укрупнённых процессов фотограмметрической обработки стереопары.
Процессы: подготовительные работы, внутреннее и взаимное ориентирование снимков, внешнее ориентирование модели, оператор-фотограмметрист должен выполнять как можно быстрее, т.к. чем быстрее эти процессы будут выполнены, тем быстрее можно будет приступить к съёмке рельефа и контуров, и тем выше будет производительность труда.
Подготовительные работы включают получение и изучение исходных материалов, а также подготовку прибора к работе.
Исходными материалами являются:
1) материалы наземной, аэро- или космической съёмки, в качестве которых могут быть чёрно-белые, цветные или спектрозональные снимки. Для АФП они должны быть отпечатаны на фотопластинках или малодеформирующихся фотоплёнках. Для ЦФС они должны быть записаны в цифровой форме на машинном носителе с помощью фотограмметрического сканера, имеющего стабильный элемент геометрического разрешения порядка 8-15 мкм и инструментальную погрешность не более 35 мкм. Сканирование снимков выполняют в том порядке, в каком они будут обрабатываться. Снимки устанавливают в снимкодержатель сканера, не допуская их разворота относительно системы координат сканера. Кроме того, нужно соблюдать в пределах каждого маршрута их ориентировку относительно местности;
2) паспортные данные фотокамеры: фокусное расстояние, расстояния между координатными метками или координаты этих меток, данные о дисторсии объектива и другие данные при использовании не кадровых фотокамер;
3) значение высоты фотографирования над средней плоскостью участка местности или значение среднего масштаба снимков;
4) элементы внешнего ориентирования снимков, если они были определены во время съёмки (данные ГЛОНАСС или GPS) или при построении сети фототриангуляции;
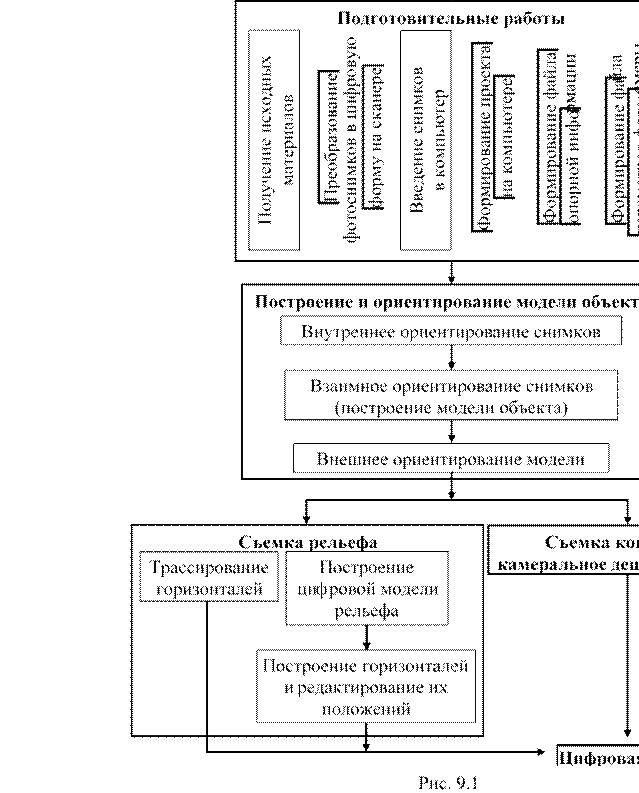
5) материалы планово-высотной подготовки снимков. К ним относятся: каталог координат опорных точек, контактные отпечатки снимков с маркированными опорными точками и описания расположения этих точек;
6) материалы полевого и камерального дешифрирования;
7) редакционные указания и ведомственные материалы картографического назначения;
8) уточнённые фотосхемы или снимки, увеличенные до масштаба составляемой карты с подписанными географическими названиями и характеристиками топографических объектов.
Вместе с исходными материалами используют инструкции, наставления, руководства, условные знаки и другие документы, касающиеся технологии проведения работ. Перед началом работы на компьютере каждый оператор задаёт рабочую директорию, а также директорию для хранения архивных копий файлов, содержащих результаты обработки.
Оператор вводит в память компьютера исходные данные, записывая их в соответствующие файлы. Кроме того, он записывает допустимую величину остаточных поперечных параллаксов, допустимые расхождения координат на опорных и контрольных точках. Последние могут задаваться как на местности, так и в масштабе снимков.
При работе на АФП:
- устанавливают увеличение наблюдательной системы прибора в зависимости от качества фотоизображения,
- проверяют в обеих ветвях наблюдательной системы установку одинаковых форм, размеров и цвета измерительных марок,
- выравнивают освещённость марок и снимков,
- выводят изображения марок на главные оптические оси глаз оператора с помощью оптических клиньев,
- устанавливают на штурвалах X, Y, Z удобных для оператора скоростей и направлений вращения,
- иногда требуется указать формат снимков и значение базиса фотографирования в масштабе снимков для задания диапазонов перемещения снимкодержателей, а также, что будет наблюдаться - диапозитивы или негативы, и как они будут располагаться на приборе - перекрытием внутрь или наружу.
9.2. Построение и ориентирование модели объекта
9.2.1. Внутреннее ориентирование снимков
Закончив подготовку прибора к работе, оператор приступает к выполнению внутреннего ориентирования каждого снимка. Порядок выполнения процесса в общих чертах следующий. Вначале измеряют координаты координатных меток, что позволит определить положения систем координат каждого снимка в системе координат прибора, а затем пересчитать измеренные координаты в системы координат снимков.
Порядок обхода меток задаётся программой. Возможен обход меток одновременно на обоих снимках, а может быть и по каждому снимку отдельно. Оператор точно наводит измерительную марку на соответствующую метку и регистрирует координаты. После этого измерительная марка перемещается на следующую метку, и процесс повторяется столько раз, сколько координатных меток занесено в файле исходных данных. Далее начинается процесс вычислений, в ходе выполнения которого координаты измеренных меток рассчитываются в системе координат снимка с началом в центре проекции. При этом в координаты вводятся поправки, учитывающие дисторсию объектива съёмочной камеры и деформацию снимка. По окончании вычислений на экране дисплея высвечиваются полученные результаты. Если они не удовлетворяют оператора, то он повторяет измерения какой либо метки или всех. Если в качестве исходных использовались паспортные значения координат координатных меток, то внутреннее ориентирование считается законченным при расхождениях измеренных величин от их паспортных значений в пределах размера пиксела, с которым был получен цифровой снимок.
9.2.2. Взаимное ориентирование снимков
(построение модели объекта)
Взаимное ориентирование снимков выполняется с целью построения геометрической модели объекта. Взаимное ориентирование снимков заключается в измерении координат шести, двенадцати (две рядом) или восемнадцати (три рядом) точках, расположенных в углах стереопары и районах главных точек снимков. Для автоматического обхода точек оператор записывает их плановые координаты в системе координат стереопары с учётом формата снимков или указывает, какое число точек будет измеряться. После включения программы взаимного ориентирования снимки автоматически раздвигаются на величину базиса фотографирования, а измерительные марки автоматические перемещаются в район первой точки взаимного ориентирования. Оператор, отключив движения одного из снимков, устраняет поперечный параллакс, наводит стереоскопическую марку на поверхность модели и регистрирует координаты. Далее измерительная марка автоматически перемещается на следующую точку взаимного ориентирования, и все описанные операции повторяются. По завершении измерений всех запланированных точек выполняется процесс вычисления, и на экране дисплея высвечиваются значения элементов взаимного ориентирования снимков, остаточные поперечные параллаксы на каждой точке и средняя квадратическая ошибка их измерения. Если на какой либо точке остаточный поперечный параллакс превышает допустимое значение, то появляется надпись с рекомендацией перенаблюдать эту точку. Взаимное ориентирование считается законченным, если остаточные поперечные параллаксы не превышают 0,015 мм при средней ошибке порядка 7 мкм.
9.2.3. Внешнее ориентирование модели объекта
Закончив взаимное ориентирование, выполняют внешнее ориентирование модели. Построенная в ходе взаимного ориентирования геометрическая модель сфотографированного объекта имеет масштаб, отличный от требуемого, и произвольную угловую ориентацию в координатной системе объекта. Чтобы привести модель к нужному масштабу и правильно сориентировать, необходимо иметь минимум три опорные точки с известными в системе координат объекта координатами. Для контроля берут четвёртую опорную точку. Точки должны располагаться в углах рабочей площади стереопары. Наличие большего числа опорных точек позволяет повысить точность внешнего ориентирования модели и выполнить вычисления с использованием метода наименьших квадратов. Вначале оператор должен измерить две или три опорные точки (в разных программах по-разному), а затем марка будет перемещаться по опорным точкам автоматически. Перемещение может происходить либо в том порядке, как эти точки записаны в файле опорных данных, либо после указания оператором её номера. По окончании измерения опорных и контрольных точек выполняются вычисления. После их завершении на экране дисплея высвечиваются элементы внешнего ориентирования модели или снимков, остаточные расхождения координат на опорных и контрольных точках, средние квадратическим ошибки, характеризующие точность ориентирования модели в системе координат объекта. Если на какой либо опорной точке расхождения координат превышают допустимую величину, то на экране дисплея появляется надпись с рекомендацией перенаблюдать эту точку.
Внешнее ориентирование модели считается законченным, когда:
- на опорных точках остаточные расхождения плановых координат станут меньше 0,2 мм в масштабе карты, а высот меньше 0,2 высоты сечения рельефа;
- на контрольных точках остаточные расхождения плановых координат станут меньше 0,3 мм в масштабе карты, а высот меньше 0,3 высоты сечения рельефа.
После завершения построения и ориентирования модели, все элементы ориентирования записывают в памяти компьютера. На АФП это позволяет после перерыва в обработке стереопары, когда прибор выключался, но снимки не вынимались из снимкодержателей, восстановить построение и ориентирование модели, не повторяя все указанные выше процессы. Если же снимки снимались с прибора, то после их укладки в снимкодержатели достаточно измерить только координатные метки обоих снимков. Вполне понятно, что измерение координатных меток нужно выполнять с особой тщательностью. Иначе не будет совпадения новых положений систем координат снимков в системе координат прибора с их прежними положениями, и новые съёмки контуров не будут состыковаться с уже нарисованными.
После выполнения внешнего ориентирования модели объекта приступают к построению цифровой модели рельефа и к съёмке рельефа и контуров.
9.3. Цифровая модель рельефа местности
Построение цифровой модели рельефа (ЦМР) местности или искусственного объекта основано на том, что положение каждой точки поверхности можно задать тремя координатами X, Y, Z в определённо ориентированной пространственной системе координат. Однако создание поля точек большой густоты очень трудоёмко, требует больших затрат времени как при измерении, так и вычислении и, кроме того, требует наличия компьютера с памятью большого объёма и с большой скоростью счёта. В то же время нет необходимости создавать ЦМР с большой густотой точек, т.к. густота их расположения зависит от рельефа местности. Например, для равнинной местности нужно измерить гораздо меньше точек, чем для горной местности. Наличие оврагов на равнинной местности вынуждает в их районе измерять больше точек. Решение задачи облегчается тем, что достаточно измерить только те точки, которые расположены в местах изменения угла ската. В результате поверхность, расположенная между этими точками, будет представлять плоскость, и можно использовать линейное интерполирование с целью определения координат расположенных между ними дополнительных точек или определения мест прохождения горизонталей с заданными высотами. Таким образом, чтобы построить ЦМР, необходимо набрать на поверхности пикеты.
Набор пикетов выполняют разными способами:
- трассированием горизонталей,
- набором хаотически расположенных точек,
- набором точек в узлах сетки квадратов,
- набором пикетов вдоль экстремальных линий рельефа (водоразделов, тальвегов (водосливов), бровок, урезов воды и т.д.) и в местах плавного изменения углов ската,
- прокладкой параллельных профилей.
Трассирование горизонталей позволяет получить послойное расположение пикетов, которые в каждом слое имеют одну и ту же высоту и похожее изменение их плановых положений. Чтобы выполнить трассирование горизонтали оператор устанавливает измерительную марку на высоту горизонтали и перемещает её вдоль поверхности. После выполнения трассирования всех горизонталей получают пирамидальное расположение слоёв пикетов с равным отстоянием по высоте друг от друга. В результате создаётся цифровая модель рельефа местности, по которой легко получить модель рельефа местности в графической форме. Интерполируя между ближними точками соседних горизонталей можно вычислить высоты точек, расположенных между этими горизонталями. Однако этот способ утомительный, т.к. требует от оператора постоянного внимательного наблюдения за движением марки. В связи с этим трассирование горизонталей целесообразно использовать, когда в пределах стереопары перепад высот такой, что нужно провести 3-5 горизонталей.
Хаотический набор пикетов требует от оператора высокой квалификации в области форм рельефа. С увеличением расчленённости рельефа необходимо набирать всё большее количество пикетов. Поиск их по площади стереопары становится трудоёмким, утомительным процессом, что приводит к пропуску точек и, соответственно, к искажению ЦМР и увеличению времени последующего редактирования. С учётом этого такой набор пикетов для построения ЦМР можно выполнять в равнинной местности при отсутствии изрезанности рельефа.
Для облегчения работы оператора и с учётом возможности автоматизации процесса набор пикетов производят по сетке квадратов. Пикеты намечают в вершинах квадратов, плановые координаты которых задают в системе координат местности или искусственного объекта. Расстояния между вершинами квадратов задают в натуральных единицах на местности. Перемещения измерительной марки по вершинам осуществляется автоматически. Высоты пикетов измеряются либо оператором, либо в автоматическом режиме с использованием коррелятора.
При выполнении измерений оператором ему приходиться вводить поправки в высотное положение измерительной марки, если она попадает на крыши домов, вершины растительности или водные поверхности. Если с крыши дома легко переместить марку на поверхность рядом с домом, то в лесном массиве, чтобы опустить её на поверхность нужно знать высоту деревьев. Если же марка попала на водную поверхность, то её нужно установить на высоте ближайшего участка берега.
При использовании коррелятора следует учитывать, что он даёт хороший результат на открытой местности при отсутствии лесных участков, населённых пунктов и водных пространств. Коррелятор даёт плохие результаты на мало контурной местности, например луг, песок, вода, т.к. в этом случае ему трудно по перемене плотности изображения найти две соответственные (одноимённые) точки. В связи с этим при использовании коррелятора приходится тратить много времени на редактирование полученных измерений, хотя имеются автоматические режимы отфильтровывания грубых измерений.
Недостатком набора пикетов по сетке квадратов является то, что положения пикетов не полностью учитывают характер рельефа местности. Чтобы ослабить этот недостаток, расстояния между вершинами квадратов подбирают с учётом расчленённости рельефа, а также заданного на создаваемой карте сечения рельефа горизонталями. Например, для плоскоравнинной местности со слабой расчленённостью и для больших сечений рельефа размеры квадратов увеличивают, а с усложнением рельефа и уменьшением величины сечения рельефа уменьшают. Однако нет гарантии, что какой либо элемент рельефа, например овраг, окажется между зарегистрированными положениями пикетов.
Следует отметить, что, хотя и задаётся вначале сетка квадратов, но в результате выполнения перечисленных выше действий плановые положения пикетов не совпадают с вершинами квадратов и, следовательно, расположение пикетов носит нерегулярный характер.
Набор пикетов вдоль экстремальных линий рельефа и в местах изменения углов ската, хотя и требует больших затрат времени, но это оправдывается при построении модели рельефной местности. С целью исключения интерполирования между точками, расположенными на противоположных скатах набор пикетов производят проведением полилиний, которые не позволяют компьютеру выполнять интерполирование между пикетами, расположенными по разные стороны от полилиний. В результате проведения полилиний и набора пикетов будет получена густая сеть точек, достаточно точно отражающая формы рельефа местности.
Недостаток набора пикетов с учётом структуры рельефа местности состоит в том, что его невозможно автоматизировать и всё зависит от квалификации оператора, его знаний форм рельефа, грамотного расположения полилиний и пикетов.
Набор пикетов прокладкой параллельных профилей позволяет систематизировать и частично автоматизировать работу оператора. В этом способе измерительная марка перемещается автоматически в заданном направлении. В задачу оператора входит следить, чтобы марка перемещалась по поверхности. Расстояния вдоль линии движения марки между точками автоматической регистрации задают в натуральных единицах на местности, во времени и в изменениях угла ската. В результате частота расположения точек регистрации меняется в зависимости от сложности рельефа местности. Расстояния между соседними линиями задают в натуральных единицах на местности. Скорость движения марки оператор регулирует с учётом изменения форм рельефа, ускоряя на ровных местах и притормаживая при изменении угла ската. При проектировании или реконструкции линейных сооружений (дорог, газопроводов, линий электропередач) ЦМР строят в виде узкой полосы вдоль предполагаемой или существующей трассы. Набор пикетов производят как вдоль трассы, так и на поперечниках, располагающихся друг от друга с интервалом 100 м и длиной плеч у поперечников 50-100 м. Однако способ параллельных профилей является утомительным для оператора, т.к. ему нужно непрерывно следить за движением марки. Из-за его усталости марка не всегда может проходить по поверхности. Кроме того, отдельные формы рельефа могут оказаться между параллельными линиями и в результате будут пропущены.
Перечисленные выше способы набора пикетов создают ЦМР из более или менее хаотически расположенных точек и представляющих собой нерегулярную сетку. Такое неравномерное, нерегулярное расположение пикетов создаёт неудобства при последующих работах. Затрудняется создание алгоритма интерполирования, например, при построении горизонталей, Частично работа облегчается с нерегулярной сеткой из квадратов (английский термин Triangular Irregular Net (TIN)). Эта сетка была предложена в 1936 г. членомкорреспондентом АН СССР, математиком и альпинистом Б.Н.Делоне. Её можно построить по набранным тем или иным способом пикетам. По сравнению с квадратом треугольник имеет преимущество, т.к. через три точки можно провести плоскость. Вершины треугольников должны располагаться на таком расстоянии друг от друга, чтобы соединяющие их стороны лежали на поверхности модели. Оператор просматривает треугольники и, обнаружив не совпадения сторон какого либо треугольника с поверхностью модели, добавляет в этом месте пикет, заменяя большой треугольник треугольниками меньшего размера. Если путём набора пикетов добиться положения, когда не только вершины и стороны треугольников лежат на поверхности, но и внутри треугольников нет выступов или провалов, то будет получена многогранная поверхность, имитирующая реальную поверхность. Эта ЦМР, несмотря на большие затраты времени на её создание, наиболее подходит для рельефных, горных районов. По этой сетке легко проинтерполировать и построить горизонтали.
Однако для поиска дополнительных точек по их плановым координатам и путём интерполирования вычисления их высот лучше всего подходит регулярная сетка, представляющая собой сетку квадратов. Задав с учётом рельефа местности размер стороны квадрата, регулярную сетку накладывают на поле измеренных тем или иным способом пикетов. Высоты точек местности, совпадающих с вершинами квадратов, компьютер рассчитывает путём интерполяции между ближайшими пикетами. Имеется вариант, когда оператор просматривает положения перекрестий сетки на поверхности стереомодели и, если какое либо перекрестие не лежит на поверхности, то измеряет рядом пикет и тем самым поправляет положение перекрестия по высоте. Полученная на основе регулярной сетки ЦМР называется матрицей высот.
Автоматическое построение горизонталей по ЦМР основано на линейном интерполировании между ближайшими точками и определении положения точек с заданной высотой. Картографическое изображение рельефа местности горизонталями предполагает зависимость высоты точки от её плановых координат: Z = F (X, Y). Следовательно, поиск положения горизонтали сводится к поиску плановых координат точек с одинаковой высотой путём интерполирования между ближайшими точками сетки, и поиска точек "входа-выхода" горизонтали из неё. При этом точки "входа-выхода" должны быть согласованы с такими же точками, найденными в соседних ячейках, где данная горизонталь проходит.
ЦМР, представляющая собой систематизированный набор цифр, не видна человеку. Чтобы зрительно воспринимать поверхность, на основе ЦМР создают матрицу, каждый пиксел которой заполняют показателями оптической плотности и цветности, снятыми с соответствующих пикселов снимка. Построенная поверхность позволяет представить рельеф местности в разных проекциях, в том числе и в более привычном для человека пространственном перспективном восприятии форм рельефа.
Для создания ЦМР используют ЦФС или АФП. На ЦФС предусмотрен ручной и автоматический режим перемещения марки. Наведение марки на поверхность выполняется как оператором, так и автоматически коррелятором. На АФП марка перемещается с помощью моторов и скорость движения можно менять. Наведение марки на поверхность выполняет оператор.
9.4. Смысл трансформирования снимков
Трансформирование снимков это преобразование изображения, полученного в одной проекции, в изображение в другой проекции. При выполнении такого преобразования нужно учитывать геометрию построения изображения в съёмочной системе:
- фиксировались ли все точки кадра в один момент времени или же изображение строилось построчно или поточечно,
- на какую поверхность проектировались точки: плоскую, цилиндрическую или сферическую.
Кроме того, нужно учитывать:
- является ли снимок горизонтальным или наклонным,
- был ли сфотографированный объект плоским или рельефным,
- каковы особенности проекции, в которой должно быть получено трансформированное изображение.
Топографическая карта представляет собой изображение земной поверхности на плоскости, полученное при условии ортогональности географической сетки, равенства масштабов и сохранения подобия фигур. При этом на поверхность референц-эллипсоида точки поверхности Земли проектируются отвесными линиями. Участки поверхности референц-эллипсоида, соответствующие трапециям топографических карт, особенно крупномасштабных, практически мало отличаются от плоскости. Таким образом, топографические карты представляют близкое к ортогональной проекции изображение земной поверхности на плоскости, а в крупном масштабе практически соответствуют ортогональной проекции, что подчёркивается названием план, а не карта.
Топографический аэроснимок является изображением точек земной поверхности на плоскости, зафиксированных в один момент времени в перспективной центральной проекции. Однако снимок имеет угол наклона относительно отвесной линии к поверхности референц-эллипсоида, что приводит к смещениям точек на снимке по сравнению с их положениями на горизонтальном снимке (см. 3.5). Правда, эти смещения подчиняются определённому закону и, если известна величина угла наклона снимка, они легко устраняются при использовании формул (5.30) перехода из системы координат снимка в систему координат местности (объекта).
Более трудной задачей при трансформировании топографических снимков является устранение смещений точек на снимке, вызванных рельефом местности (см. 3.6). Входящие в формулы (5.30) элементы внутреннего ориентирования снимка известны из паспорта фотокамеры. Элементы внешнего ориентирования могут быть получены из 1) построения сети фототриангуляции, 2) фотограмметрической обработки стереопары, в которую входит данный снимок, или 3) вычисления элементов внешнего ориентирования снимка по опорным точкам (см. 6.7). Для получения высот Z точек местности необходимо заранее по стереопарам построить цифровую модель рельефа (ЦМР), на участок местности, изображённой на снимках, подлежащих фототрансформированию. Трансформированное изображение получается практически в ортогональной проекции, поэтому такое трансформирование снимков называют ортофототрансформированием. Т.к. ортофототрансформирование выполняется по цифровым снимкам и с использование ЦМР, его называют цифровым ортофототрансформированием снимков.
Цифровое ортофототрансформирование снимков является одной из основных операций обработки цифровых снимков на ЦФС. Исходное цифровое изображение состоит из элементарных участков-пикселов, которые трансформируют каждый в отдельности с использованием значений элементов ориентирования снимка и данных цифровой модели рельефа (ЦМР). В результате ортофототрансформирования топографических снимков, особенно крупных масштабов, получают изображение практически в ортогональной проекции.
На рис. 9.2 приведена укрупнённая технологическая схема цифрового
![]() Ввод
Формирование Формирование Ввод цифровой файла данных файла
опорной
Ввод
Формирование Формирование Ввод цифровой файла данных файла
опорной
снимка информации модели рельефа
фотокамеры
Внутреннее Внешнее Ортофототрансф ориентирование ориентирование ормирование
Рис. 9.2
трансфо рмирования снимков.
Для выполнения цифрового ортофототрансформирования снимка необходимо иметь в компьютере: 1) снимок в цифровой форме, 2) данные фотокамеры, 3) каталог опорных точек, 4) цифровую модель рельефа.
Если после фототриангуляции для трансформируемых снимков были получены элементы ориентирования, то сразу приступают к цифровому ортофототрансформированию снимков. Если же элементы ориентирования снимков не известны, то сначала выполняют внутреннее и внешнее ориентирования снимков, а затем переходят к их цифровому ортофототрансформированию.
Далее поясняется смысл основных процессов при формировании трансформированного изображения в цифровой форме (рис. 9.3).

Рис. 9.3 DX
1. Вначале создают пустую матрицу трансформированного изображения.
1.1. На снимке задают границы участка изображения, подлежащего трансформированию. Обычно этот участок немного больше рабочей площади снимка, чтобы существовало перекрытие с трансформированными участками соседних снимков. Граница задаётся в виде прямоугольника.
1.2. Компьютер, используя координаты x' и y' углов участка в цифровой системе координат c'x'y'z', пересчитывает их в систему координат о'xyz снимка, а затем рассчитывает по формулам (5.30) координаты X и Y этих углов на местности. Т.к. высоты Z на местности не известны, при расчёте используется либо высота фотографирования, либо величина средней высоты, определённая по высотам опорных точек.
1.3. Задаётся размер пиксела матрицы трансформированного изображения на местности. Т.к. трансформированное изображение будет использоваться для векторизации контуров при создании карты определённого масштаба, размер пиксела рассчитывают по формуле = 0,07 M/1000 (м), где 0,07 мм - разрешение графического изображения, М - знаменатель масштаба карты.
1.4. Используя размер пиксела на местности и координаты X и Y углов участка, компьютер создаёт пустую матрицу трансформированного изображения, представляющую собой сетку квадратов. С этой целью координаты левого верхнего угла матрицы компьютер изменяет так, чтобы они стали кратны размеру пиксела, и прибавляет к ним последовательно заданный размер пиксела, тем самым строя построчно слева направо и сверху вниз пустую матрицу трансформированного изображения. В результате каждый пиксел матрицы получает координаты XI и YI.
2. Следующим этапом является заполнение матрицы изображением поверхности местности.
2.1. По координатам XI, YI каждого пиксела матрицы трансформированного изображения компьютер находит на ЦМР соответствующую ему точку и определяет её высоту ZI. ЦМР представляет собой многогранную поверхность, состоящую из четырёхугольников, которые в ортогональной проекции на плоскость представляют собой квадраты. Это позволяет путём билинейного интерполирования между ближайшими точками ЦМР с известными высотами вычислить высоту искомой точки. На рис. 9.3 для точки I такие высоты Z1, Z2, Z3, Z4. По высотам Z1 и Z2 рассчитываются высоту ZK, а по высотам Z3 и Z4 - высоту ZN, используя формулы
![]()
![]() ZK = Z1 (Z2 DZ
)D1 YI , ZN = Z4 (Z3
Z )DD4 YI .
ZK = Z1 (Z2 DZ
)D1 YI , ZN = Z4 (Z3
Z )DD4 YI .
![]() По этим высотам
рассчитываются высоту ZI по формуле ZI ZK (ZN DZK )DXI .
По этим высотам
рассчитываются высоту ZI по формуле ZI ZK (ZN DZK )DXI .
![]() Расстояния DXI,
DYI и D рассчитываются по разностям плановых координат
соответствующих точек: D = X2Y2 .
Расстояния DXI,
DYI и D рассчитываются по разностям плановых координат
соответствующих точек: D = X2Y2 .
2.2. Координаты ХI, YI, ZI компьютер подставляет в формулы (5.33) и вычисляет координаты xi и yi в системе координат о'xyz снимка, а затем в цифровой системе координат c'x'y'z'.
2.3. По вычисленным координатам xi', yi' компьютер находит на снимке пиксел, соответствующий пикселу матрицы трансформированного изображения, и определяет числовое значение оптической плотности (ОП). Если трансформируется цветное изображение, то дополнительно определяется показатель цветности.
2.4. Полученное значение ОП (и показатель цветности) придают пикселу в матрице трансформированного изображения.
2.5. Перемещаясь последовательно по матрице вдоль строк от пиксела к пикселу, компьютер выполняет операции, указанные в пп. 2.1-2.4, и, таким образом, формирует трансформированное изображение в цифровой форме и выводит его на экран дисплея.
При подключении к выходу компьютера фотопечатающего устройства или принтера с высоким разрешением трансформированное изображение можно распечатать в виде фото- или растрового изображения.
9.6. Цифровое фототрансформирование снимков равнинной местности
При трансформировании снимка равнинной местности возможен упрощённый вариант трансформирования, когда можно не использовать ЦМР. Такой вариант возможен, если в пределах рабочей площади снимка смещения rh точек, вызванные рельефом местности, не превышают допустимой величины. Чтобы рассчитать допустимый перепад высот, вызывающий такие смещения, запишем формулу (3.11) в следующем виде:
![]() h = H r
h
fm r
h ,
(9.1) r r
h = H r
h
fm r
h ,
(9.1) r r
где r - радиус-вектор угла рабочей площади снимка.
![]() Из трансформированных снимков монтируют фотоплан,
являющийся основой контурной части карты, на которой смещения точек, вызванные
рельефом местности, не должны превышать rhдоп
= 0,3 мм (рис. 9.4). Фотоплан соз даётся в более крупном масштабе, чем снимок,
поэтому смещения точек на снимке в пределах рабочей площади не должны превышать
Из трансформированных снимков монтируют фотоплан,
являющийся основой контурной части карты, на которой смещения точек, вызванные
рельефом местности, не должны превышать rhдоп
= 0,3 мм (рис. 9.4). Фотоплан соз даётся в более крупном масштабе, чем снимок,
поэтому смещения точек на снимке в пределах рабочей площади не должны превышать
![]() rh rhдоп M r
hдоп ,
(9.2) кт m
rh rhдоп M r
hдоп ,
(9.2) кт m
где кт = m/M- коэффициент трансформирования, М - знаменатель масштаба фотоплана, m - знаменатель масштаба снимка. После подстановки формулы (9.2) в (9.1) получим допустимое предельное превышение на местности.
![]() -h K Рис. 9.4
hпред = fM rrhдоп 0,3fMr . (9.3)
-h K Рис. 9.4
hпред = fM rrhдоп 0,3fMr . (9.3)
На местности превышения отсчи-
тываются от средней плоскости Е (положительные вверх, отрицательные вниз). Поэтому допустимый перепад высот Q (высота зоны) будет равен удвоенному предельному превышению, и его можно рассчитать по формуле
2fM r hпред 0,6fM
![]() Q
= 2hпред = r r . (9.4)
Q
= 2hпред = r r . (9.4)
И так, если в пределах рабочей площади снимка Q AMAX - AMIN, где
AMAX - максимальная и AMIN - минимальная высоты на местности, то в формулы
(5.30) для всех точек
снимка вместо их высот Z можно подставить высоту средней плоскости зоны: ZСР
= ![]() .
.
В результате в описанном в предыдущем параграфе порядке цифрового фототрансформирования снимков исключается этап 2.1 - определение высоты для каждого пиксела. В остальном работа выполняется также, но отличие состоит в том, трансформированное изображение будет получено в центральной проекции, а не в ортогональной. Однако отклонения точек этого изображения от положений, соответствующих условию ортогонального проектирования, не будут превышать 0,3 мм.
В таблице 9.1 приведены допустимые перепады высот Q в метрах, рассчитанные по формуле (9.4) в зависимости от величины фокусного расстояния f для масштаба карты 1:М = 1:500 при значениях rh пред = 0,3 мм, r = 70 мм (формат кадра 18х18 см) и r = 90 мм (формат кадра 23х23 см).
Таблица 9.1
|
f, мм |
70 |
100 |
140 |
200 |
350 |
500 |
1000 |
|
r = 70 мм |
0,3 |
0,4 |
0,6 |
0,8 |
1,5 |
2,1 |
4,3 |
|
r = 90 мм |
0,2 |
0,3 |
0,5 |
0,7 |
1,2 |
1,7 |
3,3 |
Чтобы получить значения Q для более мелких масштабов, надо табличные значения умножить на отношение масштаба 1:500 к масштабу карты. Например, для масштаба карты 1:1000 табличные значения Q нужно умножить на два, а для масштаба карты 1:5000 - на десять.
Для других значений фокусных расстояний табличную величину Q нужно разделить на табличную величину f и умножить на новую величину f.
На основании данных таблицы можно сделать вывод, что этот способ можно использовать при трансформировании снимков равнинной местности.
9.7. Фотоплан
Фотоплан - план местности, составленный из трансформированных снимков, который по точности планового положения контуров соответствует топографической карте.
Фотоплан может использоваться как самостоятельный вид картографического документа, так и в качестве основы для сбора векторной информации о контурной части создаваемой цифровой карты. Фотоплан составляют из рабочих площадей трансформированных снимков. Чтобы соединить соседние снимки, нужно провести на них линию разреза по середине зон продольных и поперечных перекрытий. При проведении линии нужно соблюдать следующие требования:
- линейные объекты нужно разрезать под прямым углом;
- нельзя проводить разрез вдоль линии, разделяющей объекты разного тона
(темные и светлые);
- нельзя проводить разрез через объекты, имеющие хозяйственное назначение или служащие ориентирами;
- населённые пункты нужно обходить. Если этого сделать нельзя, то разрез лучше провести по широкой улице или огородам.
В общем виде принцип соединения двух цифровых снимков состоит в следующем (рис. 9.5). Трансформированные снимки Рл и Рп должны иметь одина-
ковый размер пикселов и кратные этому размеру начала систем координат. Это обеспечивает стыковку строк в соседних снимках. Посредине перекрытия изображений проводят полилинию, которая будет линией их разреза. Пикселы, через которые проходит линия разреза, будут граничными пикселами. С учётом размеров изображений компьютер формирует матрицу фотоплана, которая должна по площади накрывать оба снимка. Там где нет изображения, пикселы матрицы останутся пустыми (белые квадраты). Каждая строка матрицы заполняется вначале соответствующей строкой левого снимка РЛ, включая граничные пикселы. Далее строка заполняется строкой правого снимка РП. Принцип соединения снимков в поперечном перекрытии остаётся таким же. Только берутся строки из верхнего и нижнего снимков и соединяются на линии разреза.
В результате компьютер формирует фотоплан.
Оценку точности монтирования фотоплана производят по трем категориям: 1) по опорным и контрольным точкам, 2) на линиях разреза соседних снимков, 3) вдоль общих рамок с соседними фотопланами или картами.
1. Остаточные расхождения плановых координат:
- на опорных точках не должна превышать 0,5 мм для равнинных и всхолмленных районов и 0,7 мм для горных районов,
- на контрольных точках, специально определённых при сгущении опорной сети с помощью фототриангуляции и не используемых при трансформировании, не должны превышать 0,7 мм в масштабе фотоплана для равнинных и всхолмленных районов и 1,0 мм для горных районов. На каждом фотоплане должно быть не менее 5 контрольных точек, расположенных равномерно по площади и имеющих разные высоты.
2. Средняя величина не совмещения одинаковых контуров на линиях разреза соседних снимков не должна превышать 0,7 мм для равнинных и всхолмленных районов и 1,0 мм для горных районов.
3. Несовмещения одинаковых контуров на рамке фотоплана при сводке с соседним фотопланом (картой) не должны превышать 1,0 мм для равнинных и всхолмленных районов и 1,5 мм для горных районов.
9.8. Съёмка рельефа и контуров по модели объекта
Съёмку рельефа выполняют только в стереоскопическом режиме. Съёмку контуров выполняют в стереоскопическом режиме или монокулярном по фотоплану. Стереосъёмка контуров выполняется при создании топографических карт на всхолмленные, горные и высокогорные районы, а также на территории с многоэтажной застройкой. Монокулярная съёмка контуров по ортофотоплану используется при создании топографических карт на равнинные и всхолмленные районы, незастроенные территории или с малоэтажной застройкой.
Стереосъёмку рельефа и контуров производят в пределах рабочих площадей стереопар. На их границах производят сводку контуров и горизонталей. Нестыковка контуров не должна быть больше 0,6 мм в масштабе карты, а одноимённых горизонталей - не больше одной трети высоты сечения рельефа. При величине заложения горизонталей менее 2 мм, нестыковка одноимённых горизонталей не должна быть больше 0,7 мм в масштабе карты.
9.8.1. Съёмка рельефа
Для съёмки рельефа в зависимости от того, на каком приборе (аналитическом или цифровом) выполняется работа, горизонтали трассируют вручную или строят цифровую модель рельефа. Трассировку горизонталей вручную целесообразно применять для равнинной, открытой, мало пересечённой местности. Для плоской местности можно использовать автоматическое построение ЦМР. В рельефной местности лучше использовать полуавтоматическое построение ЦМР, при котором оператор вычерчивает структурные линии рельефа (скелет местности), набирает пикеты на характерных точках рельефа, а затем выполняется автоматическое построение горизонталей.
При трассировке горизонталей оператор устанавливает высоту наименьшей горизонтали и находит место, где марка касается поверхности модели. Обычно эта горизонталь проходит вдоль берега реки или в низких местах, положение которых по площади модели примерно определяют по опорным точкам и материалам топографического дешифрирования. Рисовка горизонталей выполняется путём перемещения марки вдоль поверхности модели, следя за тем, чтобы она не отрывалась от неё и не повисала "в воздухе" или же не уходила "под землю". Чтобы не терять стереоскопического восприятия перемещения марки, лучше держать её чуть на отрыве от поверхности модели, оценивая её положение по высоте относительно низких мест. В этом случае ошибка в плане будет практически мала, но будет отсутствовать вероятность ухода марки "под землю". Закончив рисовку горизонтали, устанавливают отметку следующей горизонтали и рисуют её так же, как и предыдущую.
Высоту сечения рельефа не разрешается менять в пределах листа карты. Только в случае, когда соседние горизонтали расходятся на большое расстояние, на этом участке карты проводят полугоризонталь при высоте сечения рельефа, равной половине основной. Каждая пятая горизонталь, высота которой кратна 10 или 5, а при высоте сечения рельефа 2,5 м каждая четвёртая горизонталь должны быть утолщены. На крутых склонах, когда расстояние между соседними утолщёнными горизонталями становится меньше 3 мм, разрешается на этом участке карты расположенные между ними горизонтали не проводить.
При рисовке горизонталей на участках, покрытых лесом или высокой растительностью, высоту марки над поверхностью модели следует увеличить на их высоту. Последнюю можно получить по данным таксации леса и промеров, выполненных на местности. Однако большей частью высота растительности определяется фотограмметрическим способом. Для этого при подходе марки к границе лесного массива её поднимают на высоту растительности и далее ведут по вершинам. Дойдя до конца залесённого участка, марку опускают на высоту горизонтали и выводят на касание с поверхностью. Одновременно подправляют выход горизонтали из залесённого участка. Если имеются поляны, то необходимо по ним проконтролировать прохождение горизонтали. Для этого при установленной высоте горизонтали марку выводят в район поляны и проверяют её положение по высоте на всей площади поляны. При съёмке с высотой сечения 5 м нужно учитывать высоту древесной и кустарниковой растительности. При съёмке с высотой сечения 2,5 и 2,0 м необходимо учитывать высоту таких посевных культур, как кукуруза, подсолнечник, а при высоте сечения 1,0 и 0,5 м - всех остальных посевных культур, травы и т.п. Данные об их высоте на дату аэросъёмки должны содержаться в материалах высотной полевой подготовки и в редакционных указаниях.
На плоских участках местности бывает трудно определить направление ската и куда нужно вести марку. В этом случае набирают пикеты и путём интерполирования между ними определяют положения горизонталей.
Завершив съёмку рельефа, точность положения горизонталей проверяют по контрольным точкам, высоты которых были получены либо при построении сети фототриангуляции, либо в ходе полевых геодезических измерений или же набором пикетов другим оператором. Средние величины расхождений не должны превышать допусков, приведённых в таблице 9.2.
При съёмках в масштабах 1:2000 и 1:5000 с сечением рельефа 0,5 м допуск 1/4 высоты сечения, помеченный звездочкой, меняют на 1/3 высоты сечения. На лесных участках местности эти допуски увеличиваются в 1,5 раза. Количество предельных ошибок, равных удвоенной средней ошибке, не должно превышать 10% от общего числа контрольных измерений.
Таблица 9.2
|
Знаменатель масштаба карты |
500 |
1000 |
2000 |
5000 |
10000 |
25000 |
|
Плоскоравнинная местность (уклоны < 1о) |
1/4 |
1/4 |
1/4* |
1/4* |
1/4 |
1/3 |
|
Равнинная местность (уклоны 1-2о) |
1/4 |
1/4 |
1/4 |
1/4* |
1/3 |
1/3 |
|
Всхолмленная местность (уклоны 2-6о) |
1/3 |
1/3 |
1/3 |
1/3 |
1/3 |
1/3 |
|
Горная местность (уклоны 6-25о) |
1/3 |
1/3 |
1/3 |
1/3 |
1/2 |
1/2 |
|
Высокогорная местность (уклоны > 25о) |
1/2 |
1/2 |
1/2 |
1/2 |
1/1 |
1/1 |
Проведя горизонтали, измеряют характерные точки рельефа: вершины скал, холмов и курганов, бровки обрывов, мысы, насыпи, валы, выемки, отметки которых должны быть подписаны на карте. При создании карт масштабов 1:2000, 1:1000 и 1:500 измеряют также отметки полотна автомобильных и железных дорог, тротуаров и проезжей части улиц, люков подземных коммуникаций и т. п. согласно содержанию данной топографической карты. Количество таких отметок, например, на карте плоскоравнинных районов должно быть не менее 10-15 на 1 дм2.
9.8.2. Съёмка контуров
Съёмку контуров выполняют по слоям с одновременным дешифрированием и кодированием объектов. В каждом слое зарисовывают однотипные объекты: гидрография, растительность, авто- и железные дороги, сельхозугодия, населённые пункты и т. д. При этом методика, содержание и точность зависит от характера картографируемой территории: отсутствие или наличие большого числа контуров, наличие объектов, связанных с трудовой деятельностью человека. Если последние отсутствуют, то работа сводится, прежде всего, к нанесению границ природных объектов, отдельных точечных объектов, а также условных знаков, характеризующих эти объекты. Наличие населённых пунктов и промышленных объектов осложняет работу. В этом случае необходимо применять коды, с помощью которых объекты будут относиться к определённым видам. Контуры отбираются согласно требуемой нагрузке топографической карты данного масштаба. Рисовка контуров сопровождается указанием семантической информации, для чего используется классификатор топографических объектов на соответствующий масштабный ряд топографических планов и карт. Объекты, не дешифрируемые по стереомодели, отмечают в задании на полевое дешифрирование и досъёмку.
При съёмке контуров предусматривается автоматическое проведение прямой линии через две точки, окружности через три точки, замкнутые контуры можно заштриховать или заполнить условным рисунком. Если в памяти компьютера имеется библиотека условных знаков, то при наведении марки на отдельные объекты (дерево, труба, церковь и т.п.) можно подать команду на вычерчивание соответствующего условного знака. Размеры условных знаков и надписей можно изменить. Предусматриваются и другие операции. Однако все равно полностью автоматизировать решение задачи не удаётся и в ходе редактирования приходиться решать вопросы, связанные с размещением условных знаков, пояснительных надписей и т.д.
Рисовку контуров, представляющих собой извилистую линию (реки, ручьи, дороги, границы растительности и сельскохозяйственных угодий и т. п.) выполняют, проводя марку вдоль контура и удерживая её на поверхности модели. У контуров, представляющих собой ломанные линии, фиксируют положения точек поворота, которые автоматически соединяются прямыми. Объекты рисуют, последовательно переходя от контура к контуру и заполняя, таким образом, рабочую площадь стереопары. Линейные контуры следует рисовать по всей рабочей площади без разрывов. При съёмке гидрографической сети измерение урезов вод производят не реже, чем через 1 дм в масштабе карты.
При фиксировании положения высотных объектов стереоскопическую марку следует наводить на их верх (верх столба или мачты, крест колокольни и т.п.), если их основания не просматриваются стереоскопически. При рисовке зданий марку нужно наводить на углы крыши, но при этом следует учитывать свесы крыш и карнизов, если их величины в масштабе карты превышают 0,1 мм. Для этого используют данные полевых промеров или производят измерения по стереомодели при наличии стереоскопической видимости вдоль одной стороны здания. Для этого марку наводят на землю у основания здания и на край карниза. Одновременно записывают плановые координаты. По их разностям рассчитывают размер свеса карниза.
Точность съёмки контуров: средняя ошибка положения контуров местности с чёткими очертаниями относительно ближайших точек съёмочного обоснования не должна превышать 0,5 мм в равнинных и всхолмленных районах и 0,7 мм в горных и высокогорных районах. На планах территорий с капитальной и многоэтажной застройкой средние ошибки во взаимном положении точек ближайших контуров не должны превышать 0,4 мм. При этом количество предельных ошибок, равных удвоенной средней, не должно превышать 10% от общего количества контрольных измерений.
9.8.3. Сводка с соседними трапециями
После того как вся трапеция карты будет зарисована, должна быть проведена сводка по рамкам с соседними трапециями. Расхождения в положении контуров не должны превышать 1 мм на картах равнинных и всхолмленных районах и 1,5 мм на картах горных и высокогорных районах. Допустимые расхождения устраняют на половину их величины смещением контуров и горизонталей на каждом из смежных фотопланов. Если сводка производится с уже изданной картой, то исправление делается на оригинале новой съёмки.
10. СОЗДАНИЕ ТОПОГРАФИЧЕСКИХ КАРТ ПО МАТЕРИАЛАМ НАЗЕМНОЙ СТЕРЕОФОТОТОПОГРАФИЧЕСКОЙ СЪЁМКИ
10.1. Особенности выполнения наземной стереофототопографической съёмки
Наземную стереофототопографическую съёмку применяют в предгорной, горной и высокогорной открытой местности для создания топографических карт и специальных планов в масштабах 1:5000 и крупнее, когда экономически невыгодно проводить аэросъёмку и наземные методы съёмки. Её можно также применять в отдалённых, малообжитых всхолмленных районах с коротким полевым сезоном, т.к. её объём полевых работ намного меньше, чем у других видов наземных съёмок. Данный вид съёмки можно использовать для создания планов населённых пунктов, расположенных в долинах, котловинах между возвышенностями, с которых можно произвести стереофотосъёмку. Наземную стереофототопографическую съёмку можно проводить в сочетании с аэросъёмкой для создания топографических карт в масштабах 1:10000 и мельче. В этом случае по наземным снимкам можно выполнить привязку аэроснимков. Кроме того, при аэросъёмке глубокие ущелья могут стереоскопически не просматриваться, т.к. контура, расположенные в ущелье, могут изобразиться только на одном аэроснимке. Также часть территории может быть закрыта небольшим облаком. Такие "мертвые зоны" доснимают наземной стереофотосъёмкой. Однако нужно отметить, что при наземной стереофотосъёмке процент наличия "мертвых зон" выше из-за того, что возвышенность или выступ на склоне могут закрыть территории, расположенные за ними, и приходится проводить дополнительные фотосъёмочные и геодезические работы.
При выполнении стереофототопографической съёмки используют фотокамеры, в конструкцию которых входит угломерное устройство, называемое ориентирующим устройством. Оно обеспечивает установку главной оптической оси фотокамеры в заданном направлении относительно базиса фотографирования. Фотосъёмка ведется, в основном, на фотопластинки, хотя имеются фотокамер, у которых предусмотрена съёмка и на фотопластинки, и на фотоплёнки. Не у каждой фотокамеры имеется затвор, т.к. при фотографировании неподвижных объектов он необязателен. Формат кадра, в основном, прямоугольный. Длинная сторона кадра ориентируется в горизонтальном направлении. В нашей стране, в основном, использовались фотокамеры фирмы К.Цейсс: Photheo 19/1318, UMK и SMK. Фототеодолитный комплект Photheo 19/1318 был создан для использования при топографической съёмке и состоит из фотокамеры, теодолита, базисной рейки, трёх штативов. Универсальная фотограмметрическая камера UMK была создана для выполнения фотосъёмок, в основном, прикладного характера. Стереофотограмметрическая камера SMK предназначена для фотосъёмки с близких расстояний и динамических процессов. Она состоит из двух фотокамер, жестко укреплённых на штанге. Штанга с фотокамерами крепится на вертикальной стойке, позволяющей с помощью ручки менять высоту фотокамер.
В настоящее время всё большее распространение получают цифровые фотокамеры, а также лазерные сканирующие съёмочные системы. Последние позволяют получить не только изображение объекта, но и координаты его точек в заданной системе координат, что ускоряет процесс фотограмметрической обработки снимков.
10.2. Полевые и камеральные работы
Наземная стереофототопографическая съёмка какого-либо объекта выполняется с одной или нескольких фотостанций, состоящих из двух или трёх точек фотографирования. На этих точках устанавливают штативы, в трегеры которых по очереди вставляют фотокамеру, теодолит, дальномерную рейку или марку. Весь объём работ при наземной стереофототопографической съёмки делится на две части: полевую и камеральную.
В полевые работы при наземной стереофототопографической съёмке входят: рекогносцировка местности, геодезические измерения, фотографирование, фотолабораторные работы, дешифрирование. В ходе рекогносцировки местности уточняют границы съёмочного участка, устанавливают расположение пунктов геодезической сети, выбирают места расположения фотостанций, опорных и контрольных точек, намечают способы привязки станций к геодезической сети и определения координат опорных и контрольных точек. При выборе мест расположения фотостанций исходят из условия, что фотографирование всего участка должно быть произведено с наименьшего их числа. При этом число "мертвых" пространств на стереоскопическом изображении должно быть сведено к минимуму, чтобы сократить затраты на их досъёмку.
Наметив положение фотостанции и определив расстояние до ближней и дальней границы съёмочного участка, рассчитывают длину базиса фотографирования. Расчёт выполняют с учётом точности создаваемой карты. При определении по наземным снимкам трёх координат точек местности с наименьшей точностью получают отстояния, которые обозначаются координатой Y. Для повышения точности их определения нужно увеличить базис фотографирования.
Его минимально допустимую длину рассчитывают по формуле
Ymax2 mp
Bmin = ,
mY
где mY - точность определения отстояний точек, которая зависит от точности создаваемой карты, mР - точность измерения продольного параллакса.
Максимальное значение базиса фотографирования зависит от минимального отстояния Ymin точек и длины lХ стороны кадра вдоль базиса фотографирования, т.е. Bmax = Ymin xl . Следовательно, при выборе фотостанции точки f
фотографирования нужно располагать на расстоянии В, значение которого не должно выходить за пределы: Bmin B Bmax. Выбранные на местности точки фотографирования закрепляют.
После выбора положения фотостанции устанавливают границы рабочих площадей каждой стереопары, которые будут получены на этой фотостанции, и в пределах этих площадей намечают контрольные точки. Если нужно, их маркируют. В ходе выполнения на фотостанции геодезических работ измеряют геодезические координаты точек фотографирования и контрольных точек, длину базиса фотографирования. Длину базиса фотографирования измеряют как неприступное расстояние параллактическим методом с помощью теодолита и дальномерной базисной рейки. Координаты точек фотографирования определяют с помощью обратных засечек, прокладкой ходов полигонометрии и тригонометрического нивелирования. Координаты контрольных точек определяют прямыми засечками. В связи с развитием спутниковых навигационных систем их стали использовать для привязки фотостанции. Средние ошибки положения точек фотографирования, опорных и контрольных точек не должны превышать 0,2 мм в масштабе создаваемой карты, а по высоте 0,2 от высоты сечения рельефа, выбранной для создаваемой карты.
Фотографирование местности производят во время её наилучшей освещённости. Фотокамеру устанавливают на точку фотографирования, по уровням приводят вертикальную ось вращения в отвесное положение, с помощью ориентирующего устройства главную оптическую ось разворачивают в заданном направлении. Фотосъёмку с обоих концов базиса проводят в минимально короткий промежуток времени, чтобы оба снимка стереопары были получены при одинаковых условиях освещённости. Экспонированные фотопластинки проявляют на фотостанции, чтобы избежать возможного брака при определении выдержки или по другим причинам. С полученных негативов изготавливают контактные отпечатки, на которых отмечают контрольные точки и наносят результаты полевого топографического дешифрирования.
Полученные на станции снимки обладают перед аэроснимками тем преимуществом, что их элементы внешнего ориентирования определяются геодезическими измерениями с большой точностью, и, следовательно, их обработка проходит гораздо быстрее и проще, чем обработка аэроснимков. При выполнении камеральной обработки наземных снимков на стереофотограмметрических приборах собирают цифровую и графическую информацию об объекте так же, как это делается по аэроснимкам.
11. СОЗДАНИЕ КАРТ ПО КОСМИЧЕСКИМ СНИМКАМ
11.1. Особенности космической съёмки
Если грамотное выполнение аэро- и наземной съёмки обеспечивают успешное выполнение фотограмметрической обработки снимков, то объём картографической информации о поверхности планеты, получаемой по космическим снимкам, и методика фотограмметрической обработки этих снимков определяются условиями проведения съёмочного сеанса. Среди этих условий основными являются:
- вид траектории, по которой перемещался носитель съёмочной системы,
- ориентация оптической оси съёмочной системы в пространстве,
- принцип построения изображения, положенный в основу работы съёмочной системы.
Космическая съёмка производится с гораздо больших высот, чем аэросъёмка. Высоты фотографирования равны сотням и тысячам километров, поэтому по сравнению с аэроснимками космические снимки имеют более мелкий масштаб. Для того чтобы укрупнить масштаб снимков, приходится увеличивать фокусное расстояние фотокамеры, т.е. брать более длиннофокусные фотокамеры, чем используются при топографической аэросъёмке. Кроме того, высоты фотографирования во время съёмочного сеанса изменяются в больших пределах как за счёт взаимного расположения траектории и небесного тела, так и за счёт кривизны траектории и сферичности поверхности небесного тела, а это приводит к значительной разномасштабности снимков.
В связи с изменением высот фотографирования в больших пределах возрастают требования к выдерживанию продольного перекрытия снимков. При съёмке с постоянным интервалом фотографирования процент продольного перекрытия на больших высотах фотографирования будет близок к максимальному значению и начнет уменьшаться по мере приближения носителя фотокамеры к планете, достигнув наименьшего значения на минимальной высоте, а затем с удалением носителя от планеты снова будет увеличиваться. Выдерживание постоянного продольного перекрытия снимков обеспечивает электронный командный прибор, который в соответствии с показаниями доплеровского измерителя скорости и радио- или лазерного высотомера изменяет интервал фотографирования.
При космической съёмке поперечное перекрытие снимков возможно при фотографировании с орбиты спутника, когда за счёт вращения планеты при полёте носителя на следующем витке будет фотографироваться соседняя полоса поверхности. При этом в районе экватора поперечное перекрытие будет минимальным, а в районах, близких к полюсам, максимальным.
Влияние вращения планеты на выдерживание продольного и поперечного перекрытий снимков определяется углом наклонения i плоскости орбиты носителя к плоскости экватора. Например, при съёмке с экваториальной орбиты (i = 0) вращение планеты изменяет процент продольного перекрытия между снимками в маршруте. При этом поперечное перекрытие между маршрутами отсутствует. При съёмке с полярной орбиты (i = 900) вращение планеты не изменяет продольное перекрытие между снимками, но вызывает поперечный сдвиг одного снимка относительно другого, что аналогично "елочке" при аэросъёмке и может быть компенсировано разворотом фотокамеры на соответствующий угол. На промежуточных орбитах (0 i 900) факторы, указанные для крайних орбит, имеют место в той или иной степени. Правда, из-за большой скорости движения носителя съёмочной системы эти изменения практически малы.
Еще одна особенность космической съёмки состоит в том, что нужно учитывать изменение освещённости по трассе полёта из-за изменения высоты Солнца над горизонтом. В связи с этим съёмочная система должна иметь автомат регулирования экспозиции. Отсутствие его приводит к ухудшению качества снимков, потере мелких и малоконтрастных контуров и в результате к снижению измерительных и дешифровочных характеристик снимков.
Т.к. фотокамера установлена в герметичном отсеке носителя, где поддерживаются заданные температура и давление, на геометрию построения изображения оказывают влияние иллюминатор, через который производится фотографирование, и внутренняя фотограмметрическая рефракция, возникающая из-за прохождения оптическими лучами резко различных сред по обе стороны иллюминатора. В то же время при фотографировании планет, не имеющих атмосферы, отсутствует влияние атмосферной рефракции.
11.2. Виды космических траекторий
![]() При планировании каждого космического полёта выбирают
оптимальную траекторию, которая позволила бы при пролёте небесного тела, его
облёте или выходе на орбиту его спутника получить максимальную информацию при
решении разнообразных научно-технических задач. Движение космического аппарата
(КА) при условии, что на него действует притяжение только одного небесного
тела, происходит по так называемым кеплеровским орбитам, соответствующим
математическим линиям: прямой, окружности, эллипсу, параболе, гиперболе. Движение
по прямой возможно либо с бесконечно большой скоростью, либо при условии,
что вектор скорости проходит через центр притяжения. Эллиптические
траектории (рис. 11.1) являются орбитами спутников планеты, которая
располагается в одном из фокусов эллипса. Точка орби-
При планировании каждого космического полёта выбирают
оптимальную траекторию, которая позволила бы при пролёте небесного тела, его
облёте или выходе на орбиту его спутника получить максимальную информацию при
решении разнообразных научно-технических задач. Движение космического аппарата
(КА) при условии, что на него действует притяжение только одного небесного
тела, происходит по так называемым кеплеровским орбитам, соответствующим
математическим линиям: прямой, окружности, эллипсу, параболе, гиперболе. Движение
по прямой возможно либо с бесконечно большой скоростью, либо при условии,
что вектор скорости проходит через центр притяжения. Эллиптические
траектории (рис. 11.1) являются орбитами спутников планеты, которая
располагается в одном из фокусов эллипса. Точка орби-
A ты, ближайшая к центру планеты, на-
зывается перицентром , а наиболее удалённая - апоцентром А. С целью указания вокруг какой планеты летает Рис. 11.1 КА вместо слова "центр" ставят назва-
ние планеты. Например, для Земли - перигей, апогей; для Луны - периселений, апоселений и т.д. Частным случаем эллиптической орбиты является круговая орбита. Из-за постоянства значения радиуса-вектора КА, а, следовательно, высоты фотографирования круговая орбита представляет интерес для выполнения с неё космической съёмки в картографических целях. Частным случаем круговых орбит является орбита стационарного спутника, которая расположена в плоскости экватора планеты. Угловая скорость движения спутника на этой орбите совпадает с угловой скоростью вращения планеты. В результате спутник все время "висит" над одной и той же точкой планеты. Для Земли высота полёта стационарного спутника равна 35786 км. Существуют также синхронные орбиты, при полёте по которым спутник периодически появляется над заданными районами поверхности планеты вдоль трассы полёта. На этих орбитах находятся метеоспутники, телевизионные спутники, спутники связи и спутники с аппаратурой, предназначенной для исследования природных ресурсов планеты, экологической обстановки на её поверхности и т.п.
С увеличением скорости КА эллиптическая орбита начинает вытягиваться. При этом апоцентр удаляется значительно быстрее, чем перицентр. Сильно вытянутую эллиптическую орбиту можно использовать для полётов к другим планетам с возвращением. В конце концов эллипс разрывается и переходит в разомкнутую кривую, вначале в параболу, а затем в гиперболу. Параболические и гиперболические траектории используют для полётов к другим планетам в качестве пролётных или облётных, а также для доставки спутников планеты с переводом их на эллиптическую орбиту.
При полёте на КА действуют силы притяжения не только ближайшего небесного тела. В связи с этим реальные траектории имеют более сложную форму, чем указанные математические линии, и только отдельные их участки разной степени протяжённости в зависимости от заданной точности можно аппроксимировать одной из указанных траекторий. Для фотограмметристов и картографов представляет интерес форма траектории только на сравнительно небольших её участках, на которых проводятся съёмочные сеансы.
11.3. Ориентация оптической оси съёмочной системы в пространстве
В течение сеанса космической съёмки применяют два варианта расположения оптической оси съёмочной системы в пространстве. Эти варианты соответствуют двум известным случаям съёмки: параллельному и конвергентному, но при космической съёмке частным случаем последнего является отслеживание оптической осью съёмочной системы местной вертикали на поверхности планеты.
При параллельном случае съёмки (рис. 11.2) оптическая ось съёмочной системы перемещается поступательно, не изменяя в пространстве своего исходного положения. Выбор направления оптической оси в каждом случае осуществляется заранее по расчётной траектории на определённый момент времени. Например, оптическая ось съёмочной системы должна быть направлена на центр планеты либо в начале (конце) сеанса (сеансы 1 и 3), либо при прохождении перицентра траектории (сеанс 2). В выбранном направлении оптическая ось устанавливается перед началом каждого сеанса съёмки путём разворота носителя с помощью системы ориентации. Затем с помощью системы стабилизации это направление удерживается неизменным до конца сеанса. С точки
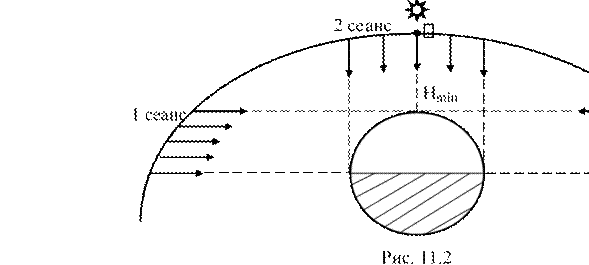
зре ния управления полётом носителя параллельное расположение оптической оси съёмочной системы является наиболее простым и применяется при съёмках с автоматических КА.
При параллельном случае съёмки взаимные углы наклона снимков близки к нулю и их величины определяются точностью работы системы стабилизации. В то же время абсолютные углы наклона снимков по отношению к вертикалям на поверхности планеты из-за её сферичности могут изменяться в течение съёмочного сеанса в пределах от 0 до 900, что вызывает большие перспективные искажения изображения, затрудняющие его дешифрирование и фотограмметрическую обработку. Поэтому для картографирования значительных по протяжённости участков поверхности планеты параллельный случай съёмки менее выгоден. Чтобы частично компенсировать этот недостаток необходимо проводить несколько сеансов съёмки, каждый из которых имеет свое направление оптической оси, как показано на рис. 11.2. Однако это усложняет управление полётом носителя съёмочной системы.
Съёмка с конвергентным расположением оптической оси съёмочной системы осуществляется путём поочередного отклонения оптической оси вперед-назад на заданный угол. Это обеспечивает повышение точности фотограмметрических измерений за счёт увеличения углов засечки на определяемые точки. Однако это усложняет управление полётом и вызывает большой расход горючего и до настоящего времени на автоматических КА не использовался.
Частным случаем конвергентной съёмки является съёмка с отслеживанием оптической осью направления местной вертикали на поверхности планеты (рис. 11.3). С точки зрения её картографирования этот вариант съёмки является предпочтительным видом съёмки, т.к. абсолютные углы наклона снимков близки к нулю и их величины определяются точностью системы, отслеживающей направление местной вертикали в подспутниковой точке. В результате перспективные искажения на снимках будут минимальными, что облегчает как дешифрирование, так и фотограмметрическую обработку. Однако съёмка с отслеживанием оптической осью местной вертикали осложняет управление полётом носителя, и при съёмках других планет с автоматических
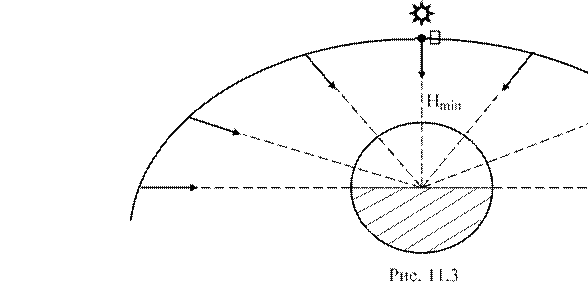
станций не применялась.
11.4. Выбор расположения съёмочных сеансов на траектории полёта
После выбора оптимальной траектории полёта космического носителя съёмочной системы на ней намечают в зависимости от задач, которые должны решаться по космическим снимкам, отдельные участки, где предполагается проведение съёмочных сеансов. Возможны следующие варианты выбора таких участков на траектории полёта при съёмке планеты: 1) при подлёте к ней или отлёте от неё; 2) в районе прохождения станцией перицентра траектории; 3) на различных участках орбиты искусственного спутника планеты. Если программой полёта предусмотрена посадка космического аппарата на поверхность планеты, то съёмка производится по аналогии с наземной фотосъёмкой, и полученные снимки используют для создания крупномасштабных карт и планов на небольшие участки.
Съёмка при подлёте к планете или отлёте от неё производится на относительно большом расстоянии с целью получения на одном кадре мелкомасштабного изображения всего полушария или его освещённой части. Такие снимки, позволяют составить общее представление об изучаемой территории, выполнить глобальное дешифрирование её поверхности, произвести измерения по лимбу планеты с целью получения цифровых характеристик её формы и размеров.
Подобные же снимки можно получить и при съёмке с пролётной траектории в районе перицентра орбиты, но в этом случае траектория должна располагаться на достаточно большом расстоянии от планеты. В этом случае получаются стереоскопические пары снимков, позволяющие создать цифровую модель сфотографированного полушария планеты и по ней подобрать референцэллипсоид, наиболее соответствующий форме и размерам планеты, а также создать опорную сеть в единой системе координат.
![]() Однако стереопару диска планеты можно получить и во
время подлёта к планете (отлёта от планеты), используя её вращение (рис.
11.4). Правда, в этом случае базис фотографирования В близок к вертикали по
отношению к её поверхности, что при съёмке вызывает, прежде всего,
разномасштабность снимков, а величины продольных параллаксов остаются малыми.
Однако за время смещения съёмочной системы из точки S1 в точку S2,
планета поворачивается на некоторый угол .
Точка М, на которую была направлена главная оптическая ось снимка, полученного
из точки S1, переместится в точку М'. В это время главная оптическая
ось снимка, полученного из точки S2, будет направлена на точку К.
Если привести положение первого снимка к моменту экспонирования второго снимка,
то нужно центр проек-
Однако стереопару диска планеты можно получить и во
время подлёта к планете (отлёта от планеты), используя её вращение (рис.
11.4). Правда, в этом случае базис фотографирования В близок к вертикали по
отношению к её поверхности, что при съёмке вызывает, прежде всего,
разномасштабность снимков, а величины продольных параллаксов остаются малыми.
Однако за время смещения съёмочной системы из точки S1 в точку S2,
планета поворачивается на некоторый угол .
Точка М, на которую была направлена главная оптическая ось снимка, полученного
из точки S1, переместится в точку М'. В это время главная оптическая
ось снимка, полученного из точки S2, будет направлена на точку К.
Если привести положение первого снимка к моменту экспонирования второго снимка,
то нужно центр проек-
ции S1 совместно со связкой проектирующих лучей переместить в точку S1'. При этом связка проектирующих лучей должна повернуться так, чтобы главный оптический луч был направлен на точку М'. В результате базис фотографирования будет равен расстоянию В' между точками S1' и S2. Этот базис будет не только в несколько раз больше В, но и расположен примерно вдоль поверхности планеты, что будет способствовать появлению продольных параллаксов и, соответственно, стереоэффекта. Правда, такой вариант съёмки можно осуществлять для планет с достаточно большой скоростью вращения, например, как у Земли. Стереоскопическую съёмку полушарий Луны можно выполнить только с пролётной траектории.
Кроме того, как видно из приведённого примера, вращение планеты искажает элементы внешнего ориентирования снимков. Снимки Р1 и Р2 получены при параллельном расположении оптических осей с вертикального базиса S1S2, т.е. их взаимный угол наклона равен нулю. В то же время из фотограмметрических определений они будут иметь взаимный продольный угол наклона, равный углу поворота планеты, и базис фотографирования S1'S2, не равный по величине и пространственному расположению реальному базису S1S2. Однако при движении носителя съёмочной системы по пролётной орбите или орбите спутника его скорость будет больше, чем скорость вращения планеты, и искажения элементов внешнего ориентирования соседних снимков будут практически малы. В то же время эти искажения будут накапливаться при маршрутной съёмке и траектория движения носителя съёмочной системы, определённая в ходе фотограмметрической обработки в планетоцентрической системе координат, будет отличаться от реальной траектории.
Съёмка из точек траектории, расположенных в районе перицентра, позволяет получить маршрут снимков в максимально крупном для данной траектории масштабе съёмки. По этим снимкам можно сгустить опорную сеть с помощью фототриангуляции и составить карту на заснятую полосу поверхности планеты.
Пролётные и облётные траектории позволяют произвести съёмку освещённого диска планеты в мелком масштабе с большого расстояния или маршрутную съёмку полосы поверхности планеты. Для картографирования поверхности планеты наиболее предпочтительными являются спутниковые орбиты. Это объясняется тем, что с них за счёт вращения планеты и увеличения угла наклона i плоскости орбиты к плоскости экватора планеты можно сфотографировать всю её поверхность. В зависимости от угла наклона орбиты делятся на экваториальные (i = 0), наклонные (0 i 900) и полярные (i = 900). С экваториальной орбиты снимают приэкваториальную полосу, ширина которой определяется углом поля зрения съёмочной аппаратуры, высотой орбиты и углом отклонения главной оптической оси от плоскости орбиты. С наклонных орбит снимают поверхность планеты, ограниченную примерно широтами С = +i и Ю = -i. Частично ширину полосы можно расширить наклонами съёмочной аппаратуры в сторону полюсов. С полярной орбиты можно отснять всю поверхность планеты, т.к. на каждом витке носитель съёмочной аппаратуры, пролетая от полюса до полюса, будет снимать новые участки поверхности планеты за счёт её вращения. В результате за полный оборот планеты можно отснять всю её поверхность.
Выбор расположения съёмочных сеансов на траектории зависит от угла между направлениями фотокамера-планета и Солнце-планета, который при съёмке освещённой поверхности планеты может изменяться от 0 до 900. Если этот угол равен 900, т.е. съёмка производится в районе терминатора - границы дня и ночи, то наличие глубоких теней, особенно на планетах, не имеющих атмосферы, затрудняет дешифрирование и фотограмметрические измерения. В то же время, если угол равен нулю, то отсутствие теней также затрудняет дешифрирование, особенно на цветных снимках. Кроме того, этот фактор ограничивает длину съёмочного отрезка траектории. Его максимальная длина примерно равна диаметру планеты (см. рис. 12.2, а, сеанс 2), если направление оптической оси совпадает с направлением линии Солнце-центр планеты. В противном случае, чем больше угол Солнце-планета-фотокамера, тем короче длина съёмочного маршрута. Например, длины первого и третьего съёмочных маршрутов короче, чем второго. В этом отношении съёмка с орбиты спутника является благоприятной, т.к. позволяет выбрать такие моменты для съёмки, когда освещённость поверхности планеты наилучшая.
11.5. Особенности фотограмметрической обработки космических снимков
Использование космических снимков для создания карт в масштабах мельче 1:100000 даёт возможность отказаться от технологии составления от крупного масштаба к мелкому. Т.к. на космических снимках имеет место естественная генерализация контуров, сокращается влияние субъективных факторов при генерализации изображения на создаваемой карте. В результате общегеографические и тематические карты создаются быстрее, и их качество повышается, т.к. картограф-составитель, меньше занимаясь вопросами, касающимися генерализации, больше уделяет внимания вопросам содержания карты.
Космические снимки получают с высот, которые на много превышают максимально допустимые высоты фотографирования, рассчитываемые по формуле (3.17),что вынуждает при фотограмметрической обработке учитывать сферичность планеты. Космические снимки охватывают большие площади плане-ты, в пределах которых сферическую поверхность планеты нельзя аппроксимировать плоскостью. Её разворот на плоскость осуществляется по формулам ма-тематической картографии. Однако каждая картографическая проекция сохра-няет точность на ограниченную территорию. Например, для топографических карт в нашей стране используется проекция Гаусса-Крюгера, в которой при фо-тограмметрической обработке аэроснимков задают координаты опорных точек, и на этапе внешнего ориентирования проблем не возникает. Но система коор-динат проекции Гаусса-Крюгера привязана к узкой полосе шириной в 60. Сле-довательно, таких систем координат на поверхности Земли будет 60, и в пределах стереопары космических снимков или одного снимка будет не одна такая система координат. При фотограмметрической обработке на этапе внешнего ориентирования снимков система координат планеты должна быть одна. В качестве такой системы координат нужно взять планетоцентрическую систе-му координат, которая является единой для всей поверхности планеты и исходной при расчёте картографической проекции.
Таким образом, обработка космических снимков должна быть произведена с учётом фотограмметрических преобразований и формул выбранной картографической проекции. В этом случае влияние сферичности планеты будет находиться в пределах, устанавливаемых для данной проекции и масштаба карты.
Строгая методика обработки космических снимков должна быть следующей.
Вначале фотограмметрическая обработка космических снимков выполняется по тем же математическим зависимостям, которые применяют при обработке аэроснимков. Вначале координаты точек поверхности планеты получают в фотограмметрической системе координат SXYZ (рис. 11.5). Например, поло-
![]()
![]() Z
Z жение точки М поверхности планеты в
Z
Z жение точки М поверхности планеты в
этой системе координат определяется
вектором RM . Далее в ходе выполнения внешнего ориентирования координаты точек поверхности планеты нужно преобразовать в систему координат, закреплённую в теле планеты. В этом процессе имеет место отличие от обработки аэроснимков. При внешнем ориентировании космических снимков нужно использовать планетоцентрическую систему координат OЦXЦYЦZЦ. Её начало OЦ совмещено с центром масс планеты. Ось ZЦ направлена в сто-
рону северного полюса и совмещена со средней осью вращения планеты. Ось ХЦ совмещена с линией пересечения плоскости экватора и плоскости нулевого меридиана. Ось УЦ дополняет систему до правой. В этой системе координат положение любой точки М поверхности планеты определяется вектором R, а положение начала фотограмметрической системы координат SXYZ - вектором
![]()
![]() RS . Три вектора связаны
уравнением внешнего ориентирования R = RS +
RS . Три вектора связаны
уравнением внешнего ориентирования R = RS +
![]()
RM = RS + NArm , где N - масштабный коэффициент, матрица A определяет
![]()
разворот системы координат Sxyz относительно системы SXYZ, а rm - вектор, определяющий положение изображения точки М на космическом снимке в его системе координат. Решение этого уравнения аналогично решению, описанному для внешнего ориентирования аэроснимков.
Если опорные точки неизвестны, то нужно использовать элементы внешнего ориентирования космических снимков в планетоцентрической системе координат OЦXЦYЦZЦ, которые определяют по орбитальным данным, полученным радиотехническими средствами, а при наличии на борту носителя звездной фотокамеры - по снимкам звездного неба. На этом завершается этап фотограмметрического определения положения точек на поверхности планеты.
Далее приступают к изображению поверхности планеты на плоскости. Для этого по формулам математической картографии рассчитывают положения
![]()
точек поверхности (вектор KM = R - RK ) в картографической системе координат OКXКYКZК, расположение которой на поверхности планеты определяется выбранной картографической проекцией.
Т.к. космическая съёмка выполняется с больших высот и длиннофокусными съёмочными системами, базис фотографирования по сравнению с высотой съёмки очень мал. В связи с этим точность измерения по стереомодели высот точек поверхности планеты не высокая, что не соответствует требованиям к измерению высот при создании топографических карт. Поэтому по космическим снимкам выполняется съёмка контуров. При этом съёмку контуров можно вести по одиночным снимкам, т.к. при съёмке с больших высот длиннофокусными съёмочными системами влияние рельефа поверхности планеты на положения точек на снимке очень мало. Правда, при внешнем ориентировании космического снимка нужно использовать не 5 опорных точек, как для аэроснимка, а желательно расположив их равномерно по площади снимка. При съёмке земной поверхности координаты опорных точек можно определить по топографическим картам крупного масштаба.
Обработка космических снимков должна производиться на цифровых фотограмметрических системах.
11.6. Особенность обработки панорамных снимков
При космической съёмке используются панорамные фотокамеры, которые позволяют за один орбитальный пролёт сфотографировать с учётом возможностей съёмочной системы практически всю освещённую поверхность планеты от горизонта до горизонта поперёк маршрута и от утреннего до вечернего терминатора вдоль маршрута. Панорамные фотокамеры относятся к сканерным съёмочным системам, выполняющим регистрацию изображения построчно (см. п. В.4). Как отмечалось, основным недостатком таких панорамных снимков является неодновремённость построения кадра, что приводит к искажению геометрии построения изображения при движении съёмочной системы относительно снимаемой поверхности.
Если фотокамера и объект съёмки неподвижны, то полученное изображе-
ние будет представлять собой центральную проекцию на цилиндрическую по-
верхность. Предположим, что из одного центра проекции S (рис. 11.6) с одним и тем же фокусным расстоянием f получены панорамный РП и кадровый Р фотоснимки. Т.к. панорамная фотосъёмка производится перпендикулярно к направлению полёта, то центральную образующую цилиндрической поверхности совместим с координатной осью х кадрового фотоснимка и будем считать её осью хП для панорамного фотоснимка. След на панорамном фотоснимке вертикальной плоскости, проведенной через главную оптическую ось So и координатную ось у кадрового фотоснимка, является центральной линией и координатной осью уП панорамного фотоснимка.
Точка местности изобразилась на фотоснимке Р в точке m', а на фотоснимке РП в точке m. Точка m' в координатной системе оху имеет координаты x = k'm', у = ok', а точка m в координатной системе oxПyП - координаты хП, уП. Причем координата уП измеряется вдоль дуги оk, радиус которой равен f, а координата хП расположена вдоль образующей цилиндрической поверхности, проведенной через точку m до точки k. Обозначим отклонение луча Sm от главной оптической оси So двумя углами и . Угол лежит в координатной плоскости Sоу. Связь между этими углами и координатами хП, уП следующая: yп , tg = xп .
=
f f
С учётом этих зависимостей найдем связь между координатами точек панорамного и кадрового фотоснимков.
![]() x
ftg
xп , y
ftg ftg yп .
(11.1) cos cos
yп f
x
ftg
xп , y
ftg ftg yп .
(11.1) cos cos
yп f
f
Таким образом, измерив в координатной системе панорамного снимка координаты точек xП, yП, преобразовывают их с помощью формул (11.1) в координатную систему кадрового фотоснимка и дальнейшую аналитическую обработку выполняют по формулам, описанным в главе 5.
Однако такая методика обработки является строгой при условии, что съёмка была произведена неподвижной фотокамерой. В этом случае изображение сетчатого поля на панорамном снимке будет иметь вид, показанный на рис. 11.7, а. Сетчатое поле хорошо иллюстрирует, как уменьшается масштаб
изображения влево и вправо от центра, что приводит к искривлению продольных линий, а также к сжатию и уплотнению поперечных.
Если фотокамера смещается относительно объекта фотографирования, то происходит перекос изображения (рис. 11.7, б). Т.к. кадр формируется, например, от левого края снимка к правому и перпендикулярно к направлению полёта, то происходит постепенный сдвиг по направлению полёта одной строки относительно другой. Исходя из технических параметров панорамной фотокамеры и условий фотосъёмки, величину смещения изображения можно вычислить и ввести в измеренные координаты поправки. При этом нужно учитывать, была ли на фотокамере установлена система компенсации сдвига изображения, которая устраняет в целом деформацию изображения, вызванную смещением фотокамеры, но из-за нестрогости работы усложняет геометрию его построения.
11.7. Принцип радиолокационной съёмки
Особенностью радиолокационной съёмки является то, что её можно проводить независимо от времени суток, погодных условий, наличия облачного покрова. Сдерживающими факторами широкого применения этой съёмки для целей картографирования поверхностей планет была низкая разрешающая способность по сравнению с фотосъёмкой и сложность обработки полученных радиолокационных изображений. Однако эти недостатки устраняются совершенствованием радиолокационной техники, записью изображений в цифровом форме, электронно-оптическими методами преобразования изображений, компьютерными методами обработки получаемой информации. Примером применения радиолокационной съёмки для целей картографирования небесных тел являются съёмки поверхности планеты Венера с АМС, т.к. из-за густого облачного покрова, окружающего её, использование съёмки в оптическом диапазоне не представляется возможным.
Радиолокаторы бывают кругового обзора (РЛКО) и бокового обзора (РЛБО). РЛКО используются для наблюдения за обстановкой вокруг точки стояния радиолокатора или вокруг его носителя. В этом случае на экране монитора окружающая обстановка изображается в азимутальной проекции. Для целей картографирования используются РЛБО с синтезированной антенной, позволяющие получать изображение с высоким разрешением. На носителе устанавливается либо одна антенна, производящая излучение радиоимпульсов вбок от линии направления съёмки (Л.Н.С.) (рис. 11.8, а), либо две антенны, произ-
водящие излучение влево и вправо. Для выполнения стереоскопической съёмки на носителе устанавливают рядом две антенны: одна производит излучение радиоимпульсов вперед, а вторая - назад. РЛБО производят излучения в миллиметровом, сантиметровом и дециметровом диапазонах радиоволн. Уменьшение длины волны приводит к повышению разрешающей способности радиолокационных изображений, но вызывают сложности в проведении съёмки. Кроме радиолокатора на борту носителя имеется радиовысотомер (РВ), измеряющий высоту полёта Н.
Принцип радиолокационной съёмки с помощью радиолокатора бокового обзора состоит в следующем. Передатчик РЛБО производит облучение радиоимпульсами (рис. 11.8, б) узкой полосы местности поперек Л.Н.С. Радиоимпульсы малой длительности следуют с определённым периодом повторения. Перерыв между импульсами служит для приема отраженных сигналов. Фронт радиоволны имеет форму дуги. В результате первыми точками местности, которых он коснется, будут точки, расположенные ближе к антенне, т.е. имеющие минимальную дальность. На рисунке это точка A и её дальность DA. Последней точкой, от которой придет отраженный радиоимпульс будет точка В, расположенная на максимальной дальности DB. Отраженные от точек местности радиоимпульсы после их приема записывает запоминающее устройство и формирует радиолокационную панораму (РЛ-панораму). Т.к. диаграмма направленности РЛБО обеспечивает радиооблучение узкой полосы местности, РЛ-панорама состоит из последовательных полос-строк, которые в свою очередь состоят из точек-радиояркостей элементарных участков местности, от которых отразился радиоимпульс. РЛ-панорама отличается от фотографического изображения, т.к. участки местности по-разному отражают электромагнитные волны радио- и оптического диапазонов. Например, участок местности может полностью отразить оптические волны и полностью поглотить радиоволны. В результате на фотоизображении будет белая точка, а на РЛ-панораме - чёрная точка.
Положение точек-радиояркостей в строке РЛ-панорамы определяется величинами наклонных дальностей, которые вычисляются согласно зависимости D = 0,5сt, где с - скорость распространения электромагнитных волн, а t - время прохождения сигнала от антенны до точки местности и обратно. На РЛпанораме прочерчивается прямая линия, соответствующая начальной дальности Do. Измерив от этой линии до определяемой точки М координату уМ, можно вычислить дальность DМ = Do + kуМ, где k - масштабный коэффициент. Последовательное соединение строк осуществляется под условием, что элементы радиояркости, имеющие одинаковые дальности, должны лежать на одной прямой.
Необходимо отметить, что рельеф местности вызывает изменение положения точки на РЛ-панораме. Например, до точки М, расположенной на возвышенности h, и до точки А, расположенной на равнине, дальности будут одинаковые: DM = DА. Следовательно, импульсы, отраженные от этих точек, придут в одно время, и на РЛ-панораме обе эти точки изобразятся в одной точке А+М'. Однако точка М должна находиться в точке М0. Таким образом, на РЛпанораме рельеф местности вызывает смещение точек (М0М') в сторону отвесной линии SN, т.е. в противоположном направлении по сравнению с тем, как это происходит на фотоизображении, получаемом в центральной проекции. Для учёта рельефа местности либо применяют стереоскопическую съёмку, либо при съёмке параллельными маршрутами используют показания радиовысотомера, который выполняет профилирование местности.
12. КАДАСТРОВЫЕ КАРТОГРАФИЧЕСКИЕ ДОКУМЕНТЫ
12.1. Краткая историческая справка о кадастре
Кадастр имеет многовековую историю. В долинах рек Тигр, Евфрат и
Нил археологи находили глиняные таблички, имеющие возраст около 5000 лет. В них описывались границы земельных участков, их площади и размеры налогообложения доходов с этих участков. Эти таблички являлись документами зарождающегося земельного кадастра.
Термин кадастр имеет двухтысячелетнюю историю. При римском императоре Августе, правившем на рубеже старой и новой эр, единицу учёта налогового сбора с участка земли назвали caputigum. Перепись людей, владеющих этими участками и живущими на них, называли caputim registrum. В последующие годы эти термины трансформировались сначала в capitastrum, а потом в catastrum. Во французском языке этот термин пишется как cadastre (лист, реестр) и означает систематизированный свод сведений, составляемый периодически или путём непрерывных наблюдений за заданным объектом. На основе этого слова появился русский термин кадастр.
Развитие и совершенствование кадастра в западноевропейских странах проходило путём обмена новыми разработками, поэтому кадастры этих стран имеют общие признаки. В целом они опираются на принципы кадастра, введённого Наполеоном во Франции в начале XIX века, основой которого являлось деление документации на две группы: текстовое описание и карты, на которых указывалось местоположение и границы земельных участков.
В нашей стране термин кадастр стал широко использоваться только с конца 70-х годов ХХ столетия, а до 1917 г. говорилось о размежевании земель, их землемерении. Планомерные работы в этой области начались после подписания 19 сентября 1765 г. Екатериной II Манифеста о Генеральном межевании земель Российской империи. На следующий год была издана "Инструкция землемерам к Генеральному всей Империи земель размежеванию". Организацией и производством работ занималась созданная в Санкт-Петербурге при Правительствующем Сенате на правах департамента Межевая экспедиция. В Москве этим занималась Межевая канцелярия, а в губерниях - межевые конторы. Было учреждено звание землемер. Указом Правительствующего Сената от 23 апреля 1779 г. Межевой канцелярии было предписано организовать подготовку специалистов-землемеров. Во исполнение этого указа 14 (27) мая 1779 г. было открыто Константиновское землемерное училище, которое в 1835 г. было переименовано в институт. В 1930 г. - институт был разделён на институт землеустройства (МИИЗ) и геодезический институт (МИИГАиК). В 1992 г. МИИЗ стал Московским государственным университетом по землеустройству, а в 1994 г. МИИГАиК - Московским государственным университетом геодезии и картографии. В обоих университетах идет подготовка специалистов по кадастру. Их также подготавливают в ряде вузов страны.
После создания землемерной службы все записи велись в писцовых книгах, которые имели финансовое и юридическое значение. В них были даны количественные и качественные описания земель, населённых мест, урожайности, а также подтверждалось дворянское происхождение владельцев земли и населённых мест, их право собственности на землю и крестьян, а также права собственности наследников. Эти записи учитывались при налогообложении.
После 1917 г. частная собственность была ликвидирована и введена коллективная собственность. Однако планомерное ведение хозяйства страны требовало кадастровой информации, и в 1977 г. Совет Министров СССР принимает постановление "О порядке ведения государственного земельного кадастра". Развал СССР, ликвидация существовавших органов управления, введение рыночной экономики и частной собственности наряду с общественной потребовало организации новой системы ведения кадастра. В 1996 г. Правительство РФ утвердило федеральную программу "Создание автоматизированной системы ведения государственного земельного кадастра Российской Федерации". В 2000 г. был принят Федеральный закон "О государственном земельном кадастре", где указано, что государственный земельный кадастр (ГЗК) это систематизированный свод документированных сведений о местоположении, целевом назначении и правовом положении земель Российской Федерации и сведений о территориальных зонах и наличии расположенных на земельных участках и прочно связанных с этими земельными участками объектов.
Использование компьютерных технологий при обработке кадастровых документов требует существования единой государственной системы классификации и кодирования кадастровой информации, чтобы её можно было передавать во все административные органы, начиная с поселка и кончая администрацией президента. Наличие такой государственной информационной системы позволяет автоматизировать весь комплекс задач кадастровой съёмки, установить оперативный контроль за состоянием и степенью использования конкретного объекта.
12.2. Виды кадастра. Кадастровые документы
В связи с тем, что в ГЗК поместить всю собираемую информацию о разных объектах нельзя, стали различать разные виды кадастра, в названиях которых слово "земельный" отсутствует. Их различают 1) по территориальному признаку, 2) по объектам учёта и видам природных ресурсов, 3) по назначению.
1. По территориальному признаку кадастры подразделяются на государственный и региональный.
2. По объектам учёта и видам природных ресурсов, помимо земельного, различают кадастры: городской, водный, лесной, месторождений и др. В каждом из них ведутся свои кадастры. Например, в городском кадастре - кадастры зданий и сооружений, подземных коммуникаций, транспорта, сферы обслуживания и т.д.
3. По назначению кадастры подразделяются на:
1) налоговый (фискальный), который ведется для характеристики земель и недвижимого имущества с целью определения порядка и размеров налогообложения;
2) правовой (юридический), который ведется для защиты прав владения собственностью;
3) многоцелевой, который содержит сведения об объектах разного типа: природных ресурсах, инфраструктуре, социально-экономических явлениях и т.д., а также обеспечивает их географической основой для решения правовых, экономических, экологических, градостроительных задач, а также проблем управления и планирования развитием территории. Таким образом, многоцелевой кадастр, обеспечивая привязку информации об объекте к его топографическому положению, включает:
- геодезическую сеть,
- топографическую базу, включающую топографические планы в масштабах 1:500 - 1:2000 для городских территорий, в масштабах 1:2000 - 1:10000 (с большой плотностью населения) и в масштабе 1:25000 с малой плотностью населения для сельской местности,
- кадастровые планы, составленные по результатам кадастровой съёмки и в соответствии с требованиями многоцелевого кадастра,
- коды недвижимости и кадастровые номера участков,
- правовые, налоговые, административные, общественно-экономические данные,
- данные о природных ресурсах и использовании земель.
В технологическом отношении ведение земельного кадастра делится на два процесса работы с информацией.
1. Проведение съёмки, включающей сбор и обработку кадастровых данных о земельных участках и об объектах, расположенных на них, а также формирование информационных моделей учётных единиц.
2. Создание банка данных, включающий учёт, систематизацию и хранение кадастровых данных, формирование информационных моделей кадастра по отдельным объектам, анализ состояния данных во времени, выдачу материалов кадастра потребителям по их запросам. С учётом многоцелевого характера кадастра банк данных должен обеспечивать полноту содержания, достоверность, актуальность, точность, единые форматы, наглядность и удобство восприятия информации.
Государственным комитетом РФ по земельной политике в 1999 г. разработана единая система технологической документации, обеспечивающая ведение государственного земельного кадастра (ЕСТД ГЗК). Документы ГЗК подразделяются следующим образом.
1. Основные документы:
- единый государственный реестр земель,
- кадастровые дела,
- дежурные кадастровые карты (планы), воспроизводящие в графической и текстовой формах сведения о местоположении земельных участков и территориальных зон.
2. Вспомогательные документы:
- книги учёта документов,
- книги учёта выданных сведений,
- каталоги координат пунктов опорной межевой сети.
3. Производные документы:
- документы, содержащие перечни земель, находящихся в собственности Российской Федерации, собственности субъектов РФ, собственности муниципальных образований;
- доклады о состоянии и использовании земельных ресурсов;
- статистические отчёты;
- аналитические обзоры;
- производные кадастровые карты (планы), воспроизводящие в графической и текстовой формах обобщённые сведения о земельном фонде, экономических, социальных, природных и иных связанных с землей процессах; - справочные и аналитические документы.
Таким образом, кадастровые документы по форме их заполнения можно разделить на текстовые и картографические. Если первые заполняют и обновляют служащие разных специальностей, то вторые создают и обновляют геодезисты, фотограмметристы, картографы.
12.3. Кадастровые картографические документы, их создание и обновление
В качестве кадастровых картографических документов используются контактные или увеличенные снимки, простые или уточнённые фотосхемы, стереофотосхемы, фотопланы (ортофотопланы), фотокарты, карты и планы.
Одиночные снимки используют при составлении земельно-кадастровых планов на равнинную сельскую местность, для контроля окружающей среды, контроля транспортных потоков в городе и др. Контура переносят с контактного отпечатка на основу плана с помощью проекционной системы или снимок увеличивают до нужного масштаба и на нём вычерчивают и записывают кадастровую информацию.
Инфракрасные (тепловые) снимки применяют для контроля теплотрасс и теплоизоляции.
Основные области применения космических снимков:
- обновление карт масштаба 1:10000 и мельче,
- контроль использования земель (загрязнение, незаконные постройки и т.д.),
- ряд задач мониторинга земель.
Фотосхемы монтируют из нетрансформированных снимков и используют при дешифрировании. Уточнённые фотосхемы монтируют из снимков, увеличенных до заданного масштаба, и наносят на неё координатную сетку. В равнинной местности они могут быть картографическим материалом первого приближения для нанесения кадастровой информации. Стереофотосхемы представляют собой две маршрутные фотосхемы, смонтированные из чётных и нечётных снимков. Их можно использовать для дешифрирования контуров равнинной и всхолмленной местности.
Фотопланы (ортофотопланы) монтируют из снимков, трансформированных и приведённых к одному масштабу. Фотоплан несет большую контурную нагрузку, поэтому он весьма перспективен для решения широкого круга задач кадастра и мониторинга городских земель.
Фотокарты получаются на основе фотопланов нанесением на них результатов дешифрирования и кадастровой информации.
Технологии создания перечисленных кадастровых картографических документов такие же, как и при создании аналогичных топографических материалов. Особенность состоит в том, что для кадастровых планов и карт пониженные требования к изображению рельефа местности. На них горизонтали либо не изображаются, либо изображаются с пониженной точностью. В связи с этим можно не проводить съёмку рельефа, а горизонтали перенести с карты более мелкого масштаба.
На земельно-кадастровой карте (плане) отражают границы административного района и границы первичных землепользований. Не изображаемые в масштабе земельные участки показывают условным знаком. Каждому землепользованию присваивают номер, под которым его учитывают в остальных земельно-кадастровых документах. Изображаются дороги, реки, здания и другие контура местности. Рекомендуются следующие масштабы для планов (карт) земельных угодий:
1:500-1:5000 - на сельские населённые пункты, города, поселки городского типа для учёта приусадебных земель, промышленных и социально-культурных объектов, а также на районы интенсивного мелиоративного земледелия;
1:10000 - на основную земледельческую зону страны;
1:25000 - на остальную земледельческую зону и степные районы с крупными массивами угодий;
1:50000 и 1:100000 - на районы отгонного животноводства, оленеводства, охотничьих промыслов и земли, не используемые в сельском хозяйстве; 1:500000 - на районы Крайнего Севера и Дальнего Востока.
Для городского кадастра с целью полноты и достоверности отображения ситуации используют планы и карты в масштабах 1:200 - 1:10000, а для крупных городов, таких как Москва, и в более мелких масштабах 1:25000 и 1:50000. На них изображают границы административного деления, улицы и площади, капитальные застройки, наземные и подземные коммуникации, гидрографию, зелёные насаждения. В дополнение приводят нумерацию кварталов и участков землепользования в общей городской системе нумерации, указывают землепользователя. В масштабах 1:500 - 1:2000 создают кадастровые планы улиц и дорог, зданий и сооружений, инженерных коммуникаций, зелёных насаждений, медицины, экологии и др.
Кадастровые планы масштаба 1:500 создают по объектам городского хозяйства на территорию учётных единиц кадастра: кадастрового участка, отрезка улицы и перекрестка. Например, эти планы создают для инженерных сетей - раздельно по каждому виду инженерных коммуникаций (водопровод, канализация, электроснабжение, связь и т. д.).
Кадастровые планы зданий и сооружений составляют в виде поэтажных планов в масштабе 1:100, на которых отображают внутренние размеры и части помещений, а также информацию о материале стен, инвентарный номер или просто номер.
Кадастровые планы и карты масштабов 1:10000 - 1:50000 издают в единой системе кодирования с отображением названий, кодов, границ города, районов, улиц, смежных землепользовании, элементов гидрографии, железных дорог, специальные обобщённые данные об объектах и явлениях городской среды. В некоторых случаях кадастровые планы этих масштабов создаются как обзорно-справочные, а масштаб определяется территорией города или района.
Кроме того, создаются отдельно:
- адресный план города;
- дежурный план красных линий и линий застройки;
- специальные планы землепользования, зелёных насаждений, жилищного фонда, транспорта и другие в масштабе, предоставляющем возможность изобразить наиболее полно требуемую информацию.
Юридическое состояние объекта (размеры, форма границы, количество строений, количество и вид ремонтов, владелец и т.д.) с течением времени изменяется, поэтому документы кадастра стареют, а они должны соответствовать фактическому состоянию объекта на момент выдачи потребителю. Следовательно, кадастровую съёмку необходимо вести непрерывно, чтобы достоверность кадастровых документов обеспечивать путём постоянного их обновления. Для этого используют материалы съёмок, проводимые организациями и службами различной ведомственной подчинённости. Полученную информацию наносят на дежурную кадастровую карту (план), с которой потом переносят её на обновляемую карту (план).
Периодичность обновления картографических документов зависит от назначения этих документов и степени их старения.
1. Если изменения контуров коснулись более 30% контурной нагрузки кадастровой карты (плана), то её создают заново.
2. Если же изменения контуров не превышают 30%, то производят обновление карты (плана).
Технологические схемы обновления кадастровых карт (планов) аналогичны применяемым схемам при обновлении топографических карт. Для этого используют материалы как новой аэро- или наземной стереофототопографической съёмки, так и наземной геодезической съёмки. Перенесение новой ситуации со снимков на план выполняют на ЦФС (АФП). Координаты опорных точек могут быть взяты из материалов прежних съёмок, если эти точки надёжно опознаются на снимках новой съёмки. Если на кадастровой карте нужно обновить рельефную часть, то горизонтали переносят на неё с обновлённой топографической карты.
13. КАРТОГРАФИРОВАНИЕ ДНА ВОДНЫХ ПРОСТРАНСТВ И СЪЁМКА ВОДНОЙ ПОВЕРХНОСТИ
13.1. Требования к технологии создания топографических карт поверхности дна водных пространств
Если картографирование суши в той или иной степени выполнено достаточно подробно, то планомерное изучение и картографирование районов земной поверхности, покрытых водой, находится в начальной стадии. Для освоения прибрежной полосы (шельфа) и подводного пространства, кроме наличия карт на эти территории и их систематического обновления, требуются также знания характеристик течений и волнения водной поверхности в заданном районе. Это необходимо для правильной застройки береговой полосы и размещения портовых сооружений, а также для разработки надёжных конструкций судов, плотин, нефтяных буровых установок. Таким образом, съёмка на водных пространствах проводится с целью: 1) картографирования поверхности дна и определения глубин, 2) определения характеристик волнения водной поверхности, 3) изучения и нанесения на карту направления и скорости течений.
Топографические карты земной поверхности, покрытой океанами, морями и внутренними водоёмами являются разновидностью и продолжением топографических карт суши. В связи с этим они должны изготавливаться по единым требованиям к содержанию и оформлению, т.е. они должны иметь единые системы координат и высот, единую разграфку, номенклатуру, масштабный ряд и унифицированные условные знаки. Хотя топографические карты земной поверхности, покрытой водой, не являются навигационными картами, однако они должны по содержанию и оформлению согласовываться с ними и могут использоваться при создании таких карт. Помимо, основных топографических карт возможно создание фотокарт, сочетающих полутоновое и графическое изображения ситуации.
Топографические карты шельфа и дна внутренних водоёмов создаются на основе материалов комплекса съемочных топографо-геодезических работ, который состоит из подготовительных работ; обеспечения съемок плановой и высотной основами; топографической съёмки побережья; съёмки рельефа дна, надводной и подводной ситуации; обработки результатов работ и составления съемочных оригиналов карт. В районах с глубинами менее 200 м съемочные работы выполняют в масштабах 1:2000-1:50000, а в отдалённых районах и с глубинами свыше 200 м - в масштабах 1:100000. Из всего комплекса работ основным определяющим процессом является съёмка рельефа дна и подводной ситуации. Съёмку рельефа дна при глубинах менее 200 м выполняют с использованием эхолота и гидролокатора бокового обзора, а при больших глубинах только эхолотом. Расстояния между галсами не должны превышать 2 см в масштабе создаваемой карты. В сочетании с методом промера используют и другие виды съёмки. Аэросъёмку морского дна применяют в прибрежной полосе. Используют также подводную съёмку. Космические снимки применяют для создания плановой части карт (фотокарт) масштабов 1:100000 и мельче.
При создании топографических карт дна должны соблюдаться следующие требования к точности планового и высотного положения нанесенных на карту объектов. Плановое положение опорных пунктов должно быть определено с точностью, не превышающей 0,2 мм в масштабе карты. Средние квадратические ошибки в положении твердых контуров и ориентиров относительно ближайших опорных пунктов не должны превышать 0,7 мм для объектов, расположенных на островах и искусственных сооружениях, связанных с государственной геодезической сетью, и 1,5 мм для остальных объектов.
Средние квадратические ошибки съёмки рельефа дна с учётом приведения к Балтийской системе высот не должны превышать 0,3 м при глубинах менеё 30 м, а при больших глубинах 1% от измеренной глубины. Подпись отметок дна должна производится до 0,1 м для глубин менее 200 м и до 1 м при больших глубинах. Средние ошибки в положении горизонталей относительно высотной основы не должны превышать 2/3 высоты сечения рельефа дна при углах наклона его элементов до 60 и целой высоты сечения при больших углах наклона. Высоту сечения выбирают в зависимости от характера рельефа дна и глубины, масштаба карты, а также с учётом величины сечения рельефа прибрежной суши, изображаемой на карте (таблица 13.1).
Таблица 13.1
|
Глубина, м |
менее 50 |
от 50 до 200 |
от 200 до 1000 |
|
Сечение, м |
от 0,5 до 10 |
от 1 до 50 |
от 10 до 100 |
Для плановой привязки положения судна во время гидролокационной съёмке используют спутниковые навигационные системы ГЛОНАСС или GPS, а также радиогеодезические дальномерные системы. Средняя квадратическая ошибка определения места судна на съемочном галсе не должна превышать 1,5 мм в масштабе съёмки относительно пунктов съемочного обоснования. С целью учёта колебаний уровня водной поверхности и привязки его к Балтийской системе высот используют наблюдения на ближайших постоянных (дополнительных) уровенных постах. Расстояния между постами устанавливают с учётом максимальной разности мгновенных уровней в любой точке участка, которую принимают равной 0,2 м для берегового уровенного поста и 0,5 м для поста в открытом море. На участках с глубинами свыше 200 м учитывают только отклонения среднего многолетнего уровня от нуля Балтийской системы высот.
13.2. Виды съёмок поверхности дна и водной поверхности
Для картографирования дна водных пространств и изучения водной среды применяют съёмки из космоса, с самолёта, с борта надводного или подводного судна, а также съёмки, проводимые аквалангистами и водолазами. В соответствии с этим выделяют космическую, аэро-, надводную и подводную съёмки. Съёмочная аппаратура используется в зависимости от того, в каком диапазоне волн будет проводиться съёмка: в оптическом диапазоне электромагнитных волн или с использованием акустических излучений.
Фотосъёмка в оптическом диапазоне электромагнитных волн может быть использована в первую очередь для съёмки водной поверхности с целью определения характеристик волнения, ледовой обстановки, степени загрязнения промышленными отходами и во время кораблекрушения. Съёмки же поверхности дна встречают препятствия, связанные со степенью прозрачности воды, а также волнением водной поверхности. Наибольшая прозрачность для световых волн незамутнённой воды приходится на волны длиной 0,460-0,540 мкм, что соответствует сине-зелёной области оптического диапазона (см. таблицу В.1). С учётом этого выбирают приёмник оптических лучей в фотокамере (фотоплёнку или матрицу ПЗС), светофильтр и искусственные источники подсветки. Волнение водной поверхности в 1-2 балла практически исключает фотосъёмку поверхности дна с самолёта или борта судна. Кроме того, волнение, поднимая донные наносы, уменьшает прозрачность воды. После шторма фотосъёмка возможна через 2-3 дня, когда восстановится прозрачность воды. С учётом сказанного фотосъёмка с самолёта позволяет картографировать поверхность дна морей и океанов до глубин порядка 15-20 м.
Аэросъёмку водной поверхности нельзя выполнять по методике, применяемой для съёмки суши, т.к. в каждый последующий момент времени её форма меняется. Если аэросъёмку водной поверхности выполнять одной фотокамерой с одного самолёта, то изображение на каждом последующем снимке будет отличаться от изображения на предшествующем, и чем больше интервал фотографирования, тем больше это отличие. В результате получить стереопару снимков не представляется возможным, и при фотосъёмке с самолёта одной фотокамерой получают одиночные аэроснимки.
Для стереоскопической аэросъёмки используют две фотокамеры с одинаковыми элементами внутреннего ориентирования и один или два самолёта. Если используется один самолёт, то фотокамеры устанавливают в специальных гондолах, укреплённых под крыльями. В этом случае базис фотографирования будет определяться размахом крыльев. Срабатывание затворов фотокамер синхронизируют с точностью 10 мкс. В результате получают одиночные стереопары волнения водной поверхности или рельефа дна. Для определения характеристик волнения фотосъёмку выполняют в масштабах 1:1000-1:3000, а для измерения рельефа дна в масштабах 1:5000-1:7000 при высоте солнца от 10-150 до 500, но не более, иначе изображение будет покрыто солнечными бликами.
При аэросъёмке с целью определения высотных отметок контуров дна используют два лазерных высотомера. Один высотомер, работающий в зелёной зоне оптического диапазона, измеряет высоту фотографирования до дна, а другой, работающий в красной зоне, до водной поверхности. Разность показаний будет глубиной, точность определения которой таким способом составляет 0,20,5 м при глубинах до 50-60 м. Высотные отметки можно определять также с помощью эхолота, установленного на судне, но в этом случае первостепенное значение приобретает взаимная привязка моментов времени получения снимков и проведения промеров.
С целью охвата большей площади водной поверхности аэросъёмку производят с двух самолётов, летящих параллельными курсами или друг за другом на расстоянии, определяющим базис фотографирования. Величину последнего рассчитывают исходя из заданной величины перекрытия снимков и высоты фотографирования. Чтобы уменьшить площадь стереопары, подсвеченной бликом от солнца, кроме указанных выше условий, базис фотографирования выбирают больше 0,05Н - 0,1Н и располагают перпендикулярно к направлению на солнце. По результатам стереоизмерений длины волн определяют с точностью 3-5%, их высоты - 20-30 см.
Специфика аэросъёмки водной поверхности и рельефа дна накладывает ряд требований на фотокамеру и самолёт. Фотографирование водной поверхности проводится при пониженной освещенности из-за малых высот солнца. К этому нужно добавить слабую контрастность водной поверхности и рельефа дна. С целью снижения влияния дымки используют жёлтый светофильтр ЖС12, что уменьшает силу светового потока. Более плотные светофильтры при фотосъёмке рельефа дна применять нельзя. Все это требует, чтобы фотокамера имела светосильный объектив. Для исключения подсветов боковыми лучами используют бленду. Для аэросъёмки рельефа дна нецелесообразно применять как короткофокусные, так и длиннофокусные фотокамеры. У короткофокусных фотокамер с увеличением углов пересечения оптических лучей с водной поверхностью на краях кадра происходит падение резкости изображения. У длиннофокусных фотокамер резкость уменьшается из-за смаза изображения. Что касается самолёта, то для аэросъёмки в районах, удалённых от берега, наиболее подходят самолёты с большой дальностью полёта или гидросамолёты. Для аэросъёмки районов шельфа и прибрежной полосы лучше использовать самолёты со средней дальностью полёта. Прибрежные морские и океанские пространства, а также озёра и реки лучше фотографировать с лёгких самолётов.
Фотосъёмку волнения водной поверхности производят также с берега и борта судна. Фотосъёмку двумя фотокамерами с борта судна можно сравнить со съёмкой двумя фотокамерами с самолёта. Недостатком фотосъёмки как с борта судна, так и берега является то, что фотографируется только передний склон волны и её вершина. Чтобы частично ослабить этот недостаток, фотокамеры устанавливают по возможности на максимальную высоту. Т.к. фотосъёмка проводится с небольших по сравнению с аэросъёмкой отстояний, полученные фотоснимки представляют крупномасштабные изображения волн, по которым можно получить с высокой точностью полную количественную характеристику всех их элементов. Кроме того, с борта судна фотографируют обрывистые берега с целью определения взаимодействия суши и воды.
При производстве подводной съёмки отстояния съемочной аппаратуры от дна зависят от глубины погружения, степени замутнённости воды и мощности искусственных осветителей. Подводное фотографирование, производимое аквалангистами и водолазами, выполняют выборочно для повышения достоверности дешифрирования объектов дна. Большая замутнённость воды в реках и озёрах не позволяет использовать фотосъёмку для картографирования поверхности дна. Специфика подводной фотосъёмки состоит в том, что фотокамера устанавливается перед иллюминатором подводного аппарата, управляемого человеком непосредственно или дистанционно. При большом удалении фотографируемых объектов, когда отстояния больше 100f, плоскопараллельный иллюминатор не вызывает смещения точек на фотоснимке и формулы связи координат точек дна и фотоснимка выводят с учётом двухсредности: вода-воздух. Если отстояния соизмеримы с фокусным расстоянием, то проектирующие лучи не будут параллельны, и иллюминатор будет оказывать влияние на геометрию построения изображения. Формулы связи координат в этом случае должны учитывать трёхсредность: вода-стекло-воздух.
Особенность фотосъёмки поверхности дна из космоса состоит в том, что на космических снимках рельеф дна виден на гораздо больших глубинах, чем на аэроснимках. Однако при этом фиксируются только крупные формы рельефа, имеющие размеры в сотни и тысячи метров, т.к. происходит естественная генерализация контуров. Это объясняется тем, что при фотосъёмке с больших высот волнение водной поверхности не искажает изображения поверхности дна, т.к. смещения точек изображения, возникающие из-за этого фактора, меньше разрешающей способности фотоизображения. Кроме того, оптические лучи, отразившиеся от дна и несущие изображение его точек, при прохождении водной среды к её поверхности сильно ослабевают за счёт поглощения и рассеивания. В результате до объектива фотокамеры, расположенной на самолёте, доходят ослабленные лучи, которые и формируют в фокальной плоскости фотокамеры изображение деталей поверхности дна, расположенных на небольших глубинах. В то же время рассеянные лучи также формируют изображение, однако оно получается увеличенным за счёт расплывчатости, размытости. Степень размытости зависит от свойства водной среды и её глубины: чем больше глубина, тем больше размытость контуров. При расположении фотокамеры на небольших высотах над водной поверхностью размытое изображение не фиксируется на фотоплёнке. Когда же фотокамеру поднимают на большую высоту, линейные размеры размытых изображений контуров поверхности дна уменьшаются в фокальной плоскости фотокамеры до точечных размеров, что позволяет фиксировать чёткое изображение. Полученные фотоснимки позволяют создавать нетопографические карты, на которых будут отображены формы рельефа дна морей и океанов размерами от сотен до тысяч метров при глубинах в несколько сотен метров. Поверхность дна озёр, водохранилищ, рек также просматриваются из космоса, но на небольшие глубины из-за замутнённости воды. Исходя из опыта выполнения космической фотосъёмки, наилучшие условия для её проведения с целью съёмки дна водных пространств будут следующие: углы отклонения главной оптической оси фотокамеры от отвесной линии не должны превышать 30-400, высота Солнца над горизонтом должна быть 30-600, а направление от Солнца 90-1300.
Принцип лазерной съёмки поверхности дна с подводных и надводных судов заключается в том, что лазерным лучом, сканируют поверхность дна и изображение формируется поточечно. Для того чтобы луч света проникал в толщу воды, он должен иметь длину волны, соответствующую сине-зелёной области оптического диапазона электромагнитного спектра. Дальность действия данной системы зависит от замутнённости воды и мощности лазера.
Для гидроакустической съёмки непрозрачность воды не является препятствием, т.к. акустические волны могут распространяться в толще воды на большие расстояния без значительных потерь силы сигнала и даже проникать на некоторую глубину в осадочные породы. Скорость распространения звуковых волн в воде равна в среднем 1,5 км/с, что в 2.105 раза меньше, чем скорость радиоволн в воздушной среде, но в воде радиоволны быстро затухают. Гидроакустическая съемочная аппаратура позволяет проводить съёмку поверхности дна как на шельфе, так и на больших глубинах. С её помощью можно выявить площади распространения различных грунтов и покрывающей их растительности, обнаружить подводные кабели и трубопроводы, затонувшие суда.
В качестве гидроакустической съемочной аппаратуры используют эхолоты, звуковизионные и голографические системы, гидролокаторы. Аппаратура может устанавливаться как на надводных, так и подводных судах. Принцип работы эхолота основан на непрерывном промере глубин вдоль направления движения судна. При съёмке площади судно двигается параллельными курсами-галсами. Общую картину поверхности дна составляют путём совместной обработки параллельных профилей. Такой вид съёмки имеет многолетнюю историю, в течение которой конструкция эхолотов непрерывно совершенствовалась. Недостатком эхолотных измерений является большая частота промерных галсов. Уменьшение их частоты приводит к пропускам форм рельефа и ситуации в промежутках между галсами. Кроме того, с увеличением глубины происходят пропуски мелких контуров и форм рельефа, и выписываемый эхолотом профиль является генерализованным. В связи с этим, если нужно регистрировать мелкие контура и формы рельефа дна, антенну эхолота устанавливают на носителе, погруженном на глубину и буксируемом судном.
Звуковизионные системы позволяют получить изображение дна путём преобразования акустических волн в оптические и демонстрации на экране монитора, а также регистрации их на электронном или магнитном носителе. Такие системы рассчитаны на применение на мелководье (глубины до 50 м) при сильно замутнённой воде.
Для получения изображений поверхности дна используют голографические акустические системы. Акустические волны, созданные когерентным излучателем, отражаются от дна и после приема поступают в блок обработки, где они совмещаются с опорным сигналом. В результате полученная акустическая голограмма с помощью цифровой или оптической техники преобразуется в оптическое изображение объекта. Особенность состоит в том, что при освещении голограммы опорным лучом происходит искажение изображения по глубине, т.к. длины волн, создаваемых оптическим лазером при восстановлении изображения, не соответствуют длинам звуковых волн.
Гидролокаторы бокового обзора позволяют решить задачу картографирования поверхности дна рек, озёр и морей на глубинах до 200 м, а в дальнейшем, по мере их совершенствования, всей земной поверхности, покрытой водой. Особенности гидролокационной съёмки описаны в 13.5.
По аэроснимку глубины или характеристики волн можно определить фотометрическим, фотограмметрическим или дифракционным способом.
Фотометрический способ применяют для определения глубин прибрежной полосы, где глубины не превышают 10 м. В этом случае аэросъёмку проводят так, чтобы на аэроснимке изобразился участок суши. Масштаб фотографирования выбирают в пределах 1:3000-1:10000 и используют фотокамеру с f = 200 мм. Съёмку производят в зелёной зоне оптического диапазона. При этом вода должна быть прозрачной, а отражательная способность грунтов дна одинаковой. Глубины рассчитывают по фотометрическим измерениям перемены плотности изображения, начиная от береговой линии. Измерения выполняют на регистрирующем микрофотометре. Точность определения глубины 10%.
![]() При фотограмметрическом
способе длины волн вычисляют по формуле L = lm, где m - знаменатель масштаба
аэроснимка; l - расстояние между гребнями волн, измеренное на аэроснимке.
Точность определения 8-12%. Зная длину волны при достаточно больших глубинах
можно вычислить её скорость по gL 2.
При фотограмметрическом
способе длины волн вычисляют по формуле L = lm, где m - знаменатель масштаба
аэроснимка; l - расстояние между гребнями волн, измеренное на аэроснимке.
Точность определения 8-12%. Зная длину волны при достаточно больших глубинах
можно вычислить её скорость по gL 2.
формуле V = , где g = 9,81 м/с
2
Для определения скорости волн проводят аэросъёмку с заданным продольным перекрытием так, чтобы на соседних снимках изобразились неподвижные объекты (острова, искусственные сооружения). Измерив на перекрывающихся снимках смещение одной и той же волны относительно неподвижm
ного
объекта, вычисляют её скорость по формуле V = ![]() , где - интервал фо-
, где - интервал фо-
тографирования. Точность определения составляет 20%.
Для определения направления и скорости течения производят прокладку двух аэросъемочных маршрутов через заданный интервал времени между неподвижными объектами, предварительно разбросав поплавки. Определив положения поплавков относительно неподвижных объектов на каждом маршруте, а затем их взаимное смещение, происшедшее за время между прокладкой маршрутов, находят направление и скорость течения. Точность определения 20%.
Дифракционный способ применяют для определения по аэроснимкам длин волн. Он основан на том, что взволнованная водная поверхность имеет периодический характер и её изображение на аэроснимке можно рассматривать как несовершенную дифракционную решётку. Измерения производят на специальной дифракционной установке. Точность определения длины волны 3-5%.
При фотосъёмке рельефа дна оптические лучи, идущие от точек дна к фотокамере, проходят последовательно две среды: водную и воздушную (рис. 13.1). На границе этих сред из-за различия значений их коэффициентов преломления nвд и nвз оптические лучи преломляются, т.е. подойдя к поверхности воды под углом уходят от неё под углом . Согласно закону преломления
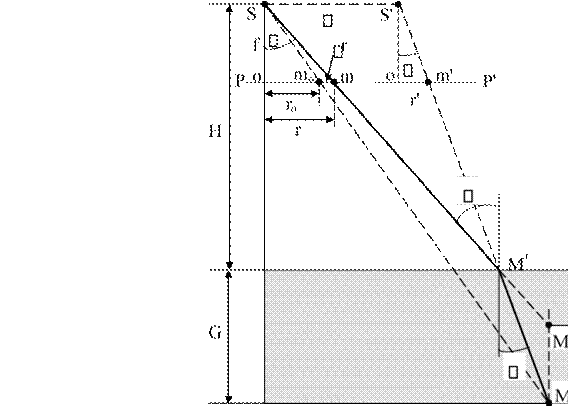
связь между углами и определяется соотношением
nвд sin = nвз sin. (13.1)
Оптический луч, идущий от точки М дна, пройдя путь MM'S, зафиксирует её изображение на горизонтальном снимке Р, расположенном над поверхностью воды на высоте Н, в точке m с радиусом-вектором om = r. Если бы водной среды не было, то точка M изобразилась бы на фотоснимке в точке mo с радиусомвектором ro. Величина r - ro = r является смещением точки на снимке под влиянием глубины G водной среды. Из геометрических соотношений запишем (H G)(r r) Hr
![]() Gtg f f
Gtg f f
и после преобразований получим
r
= ![]() G(r
ftg )
. (13.2)
G(r
ftg )
. (13.2)
H G
На основании формулы (13.1) запишем
1 tg = . (13.3)
![]() n2 вдsin2 2 1
nвз
n2 вдsin2 2 1
nвз
Величину угла можно выразить через значения r и f:
sin2 = ![]() 2r2 r2
, tg
=
2r2 r2
, tg
= ![]() fr .
(13.4) f
fr .
(13.4) f
Подставим формулу (13.4) в формулу (13.3). При этом учтем, что значение коэффициента преломления воздуха мало отличается от единицы (nвз = 1,00027), и в земных условиях значение коэффициента преломления воды берут относительно воздуха (n = 1,33299). После преобразований и замены nвд на n формула (13.3) примет вид
Подставив формулу (13.5) в формулу (13.2), получим формулу расчёта смещения точки на горизонтальном снимке под влиянием глубины
![]() 1 1
1 1
r = Gr. (13.6)
H G
![]()
![]() На основании формулы (13.6) можно сделать вывод, что на
фотоснимке только одна точка, расположенная на отвесной линии (r = 0), не
смещается под влиянием глубины водной среды, а также, что смещения точек на
короткофокусных фотоснимках будут больше, чем на длиннофокусных. По формуле
(13.6) можно получить формулы смещения x
и y точки
вдоль координатных осей горизонтального фотоснимка. Для этого подставим в неё r2
= х2 + у2 и учтем, что х
= х r и у = у r . В результате получим
На основании формулы (13.6) можно сделать вывод, что на
фотоснимке только одна точка, расположенная на отвесной линии (r = 0), не
смещается под влиянием глубины водной среды, а также, что смещения точек на
короткофокусных фотоснимках будут больше, чем на длиннофокусных. По формуле
(13.6) можно получить формулы смещения x
и y точки
вдоль координатных осей горизонтального фотоснимка. Для этого подставим в неё r2
= х2 + у2 и учтем, что х
= х r и у = у r . В результате получим
r r 1
![]() 1
1
x Gx
H G (13.7)
1
![]() 1
1
y Gy
H G
Из анализа формул (13.7) можно сделать вывод, что на стереопаре одноименные точки, имеющие на левом и правом снимках разные координаты, смещаются на разные величины, что осложняет обработку и искажает конечные результаты.
Поперечные параллаксы не искажаются на линии базиса, т.к. для точек на этой линии у = 0, и на перпендикуляре к базису, проведенном через его середину, т.к. для точек, расположенных на нём, хл = хп, ул = уп и, следовательно, ул = уп. В углах же стереопары одноименные точки из-за неравенства абсцисс будут иметь разные смещения y. В результате происходит нарушение компланарности одноименных проектирующих лучей. Хотя неравенство смещений точек частично можно компенсировать изменением угловых элементов ориентирования фотоснимков, их взаимное ориентирование практически выполнить нельзя, и по площади стереопары остаются поперечные параллаксы.
Продольные параллаксы искажаются для всех точек стереопары: меньше на линии базиса и максимально в углах стереопары. Причем для всех точек значения продольных параллаксов изменяются в сторону увеличения, а это приводит к тому, что измеренные по стереопаре фотоснимков глубины G' (см. рис. 13.1) не соответствуют истинным значениям G. Связь между ними определяется равенством Gtg = G'tg, а с учётом формул (13.4) и (13.5) формулой
1
G G'. (13.8)

Таким образом, аналитическая фотограмметрическая обработка фотоснимков поверхности дна состоит из двух этапов. На первом этапе вычисляют координаты точек дна, используя методику обработки, принятую для аэроснимков. Затем по формуле (13.8) вычисляют реальные глубины и, используя их значения, по формулам (13.7) определяют поправки в измеренные на фотоснимках координаты. На втором этапе, используя исправленные координаты, повторяют вычисление координат точек поверхности дна.
Возможна и несколько иная методика обработки подводных снимков. Если предположить, что в точке М' (см. рис. 13.1) не произойдет преломления оптического луча, и он пойдет по линии M'S', то в плоскости снимка P' получим точку m', имеющую радиус-вектор r'. Связь между радиусами-векторами r и r' можно определить из равенства
Hr Hr'
![]() ,
f f
,
f f
после преобразования которого получим формулу f
r' = r - ![]() ,
(13.9)
,
(13.9)
H
где = Н(tg - tg) - смещение центра проекции вдоль линии базиса фотографирования из точки S в точку S'. Учитывая формулы (13.4) и (13.5), получим
1 1
Hr . (13.10)
. (13.10)
f
Подставив формулу (13.10) в формулу (13.9), получим связь между радиусами-векторами r' и r, что согласуется с формулой (13.5), т.к. r' = f tg. r r' = . (13.11)

![]() Формулы
(13.11) и (13.10) можно записать через проекции на координатные оси
радиус-векторов и через смещения
с учётом равенства отношений x' y' r' x
y
. Полученные выражения
подставляют в формулы
Формулы
(13.11) и (13.10) можно записать через проекции на координатные оси
радиус-векторов и через смещения
с учётом равенства отношений x' y' r' x
y
. Полученные выражения
подставляют в формулы
и
x y r x y r
связи координат точек пары снимков и местности. Например, для идеального случая фотосъёмки формулы будут иметь вид
1
1
|
p' л Z f |
f |
л 0 |
![]() X x'л x'л
X x'л x'л
Y ![]() B'y' H y' ,
B'y' H y' ,
где В' = В - ![]() H(p
p') .
f
H(p
p') .
f
Описанная методика обработки больше подходит для подводных снимков, полученных спаренными фотокамерами. В этом случае Н будет расстоянием от передней узловой точки объектива до границы раздела воздушной и водной сред.
Обработка снимков поверхности дна на стереофотограмметрических приборах имеет ряд особенностей. Из-за искажений поперечных параллаксов происходят деформации продольных и поперечных угловых элементов ориентирования снимков. После выполнения взаимного ориентирования имеются остаточные поперечные параллаксы, которые нужно устранять на каждой точке смещением правого снимка относительно левого по оси у. Горизонтирование модели выполняют либо по точкам водной поверхности, считая её горизонтальной, либо по высотным отметкам контуров дна, введя в показания счётчика высот поправки согласно формуле (13.8). При рисовке горизонталей модель нужно разделить на зоны, в пределах которых согласно заданной точности можно считать значение подкоренного выражения в формуле (13.8) постоянным, и выполнять рисовку горизонталей, вводя поправки в показания счётчика высот. Стереофотограмметрический способ позволяет определять глубины с ошибкой примерно 30-40 см.
Приведенные выше выводы формул сделаны при условии, что волнение водной поверхности отсутствует, и течение водных слоев носит ламинарный характер с плавной переменой температур и давления по мере увеличения глубины. Если же поверхность взволнована, а также имеет место турбулентное течение водяных слоев, то картина дна искажается: соседние контуры сближаются или расходятся, возможно, пропадание контуров. Точность измерений по снимкам снижается также из-за нерезкости изображения контуров дна, появляющейся под влиянием следующих факторов: увеличения глубины и угла поля зрения фотокамеры, укрупнения масштаба фотосъёмки. Под действием этих факторов увеличивается кружок нерезкости, возникающий из-за разделения водной средой оптического луча на отдельные монохроматические лучи. Добавив к этому указанные выше ограничения из-за непрозрачности воды и быстрой поглощаемости ею световой энергии, можно отметить, что фотосъёмка не является производительным методом при топографическом картографировании поверхности дна, поэтому предпочтение отдаётся гидролокаторной съёмке, прежде всего, с помощью гидролокатора бокового обзора с синтезированной апертурой.
Специфика использования космических снимков при картографировании поверхности дна состоит в том, что из них можно составить фотопланы, а нанесение на них горизонталей выполнять после гидроакустической съёмки эхолотом или гидролокатором бокового обзора. Это объясняется тем, что точность измерения глубин по космическим снимкам из-за большой высоты фотографирования будет соизмерима с глубинами.
13.5. Гидролокационная съёмка поверхности дна
Принцип действия гидролокатора бокового обзора (ГЛБО) аналогичен принципу действия радиолокатора бокового обзора (РЛБО), рассмотренного в
п. 11.7. При съёмке на мелководье антенны устанавливают по левому и правому бортам судна, а при съёмке глубоководного района - на носителе, буксируемом на тросе и погружённом на заданную глубину с целью снижения влияния волнового колебания и рефракции акустических волн в поверхностном слое.
ГЛБО производит съёмку поверхности дна полосами слева и справа от движения судна, регистрируя наклонные дальности D аналогично РЛБО (см. рис. 11.8). Величины наклонных дальностей D вычисляют согласно формуле D = 0,5ct, где с - скорость распространения звуковых волн под водой; t - время прохождения звуковой волны от антенны до точки на дне и обратно. Т.к. скорость звуковой волны может изменяться в зависимости от характеристик водной среды, то её необходимо измерять во время съёмки, для чего используют специальные измерители скорости звука.
Снимок, полученный с помощью ГЛБО, так же как и у РЛБО, представляет собой длинную полосу, составленную из строк профилирования дна перпендикулярно направлению движения судна. В каждой строке регистрация изображения начинается от нулевой отметки, затем строится изображение контуров поверхности дна, начиная с наиболее близкой точки и кончая наиболее удалённой, расположенной на пределе дальности действия ГЛБО. Изображение выводят на экран монитора и записывают на электронный носитель, фотоплёнку и бумажную ленту.
Чтобы плановые координаты точек дна привязать к береговой системе координат, во время гидролокаторной съёмки выполняют привязку положения судна по видимым береговым ориентирам или радиотехническими и навигационными системами. Для привязки глубин к Балтийской системе высот регистрируют уровень водной поверхности во время съёмки. Если антенна располагается не на судне, а на носителе, транспортируемом на тросе, в координаты Х, У, Z нужно вводить поправки за несовпадение антенны с судном.
Для целей картографирования поверхности дна водных пространств используют гидролокаторы с дальностью действия до 400-600 м. Увеличить дальность действия можно путём уменьшения частоты излучаемых звуковых волн, но это приводит к уменьшению разрешающей способности получаемого изображения. Увеличение же частоты акустических колебаний приводит к их быстрому затуханию в водной среде. Увеличить дальность действия при сохранении разрешающей способности позволяют гидролокаторы бокового обзора с синтезированной апертурой ГЛБОСА, в работе которых применён принцип акустической голографии. У ГЛБОСА по мере движения антенны амплитуда и фаза принимаемых сигналов записываются запоминающим устройством и когерентно суммируются с ранее принятыми сигналами. Вычислительное устройство обрабатывает информацию, представленную в цифровом виде, и формирует изображение элементарных участков поверхности дна. Разрешающая способность у ГЛБОСА составляет примерно 1 м при дальностях до 1 км.
Особенность гидролокационной съёмки состоит в том, что полученное изображение не является основным и единственным носителем информации. Оно является более дешифровочным, чем измерительным. Основной поток информации уже в ходе съёмки проходит предварительную обработку с учётом принципа работы съемочной аппаратуры и формул связи координат. Дальнейшая обработка информации в компьютерах позволяет определить в заданной системе координат координаты каждой точки изображения и построить цифровую модель сфотографированного объекта, преобразовать исходное изображение в картографическую проекцию с одновременным повышением его качества, вычислить необходимые характеристики объекта: профили, площади и тому подобное. Такой принцип получения исходной информации позволяет передавать её по каналам радиосвязи и приступать к обработке, не дожидаясь возвращения носителя съемочной аппаратуры на базу. Использование компьютера облегчает обработку материалов гидролокационной съёмки, а при сочетании её с фото- или лазерной съёмкой и создания на этой основе банка эталонов дешифрирования будет облегчено опознавание подводных объектов.
1. Инструкция по фотограмметрическим работам при создании цифровых топографических карт и планов. - М.: ЦНИИГАиК, 2002. - 100 с.
2. Лобанов А.Н., Буров М.И., Краснопевцев Б.В. Фотограмметрия.
- М.: Недра, 1987. - 309 с.
3. Максудова Л.Г. Основы городского и земельного кадастра.
Учебное пособие. - М.: УПП "Репрография" МИИГАиК, 2003. - 178 с.
Сокращения, принятые в топографо-геодезическом производстве
|
АГП |
Аэрогеодезическое предприятие |
|
АГС |
Астрономо-геодезическая сеть |
|
АФА |
Аэрофотоаппарат |
|
АФП |
Аналитический фотограмметрический прибор |
|
ВГС |
Высокоточная геодезическая сеть |
|
ВТУ |
Военно-топографическое управление Генштаба |
|
ГВО |
Главная высотная основа |
|
ГГС |
Государственная геодезическая сеть |
|
ГИС |
Геоинформационная система |
|
ГЛОНАСС |
Глобальная навигационная спутниковая система |
|
ГСС |
Геодезические сети сгущения |
|
ГДП |
Геодинамический полигон |
|
ГФГС |
Государственная фундаментальная гравиметрическая сеть |
|
ИВЦ |
Информационно-вычислительный центр |
|
ИПС |
Информационно-поисковая система |
|
ИСЗ |
Искусственный спутник Земли |
|
КА |
Космический аппарат |
|
КС |
Космическая съёмка |
|
МАГП |
Московское аэрогеодезическое предприятие |
|
НЛ |
Номенклатурный лист |
|
НТА |
Нормативно-технический акт |
|
ПО |
Программное обеспечение |
|
РТМ |
Руководящий технический материал |
|
СГС |
Спутниковая геодезическая сеть |
|
СИФ |
Справочно-информационный фонд |
|
ТГП |
Техногенный геодезический полигон |
|
ТИГГН |
Территориальная инспекция государственного геодезического надзора |
|
ФАГС |
Фундаментальная астрономо-геодезическая сеть |
|
ЦКГФ |
Центральный картографо-геодезический фонд |
|
ЦММ |
Цифровая модель местности |
|
ЦМР |
Цифровая модель рельефа. |
|
ЦТИ |
Цифровая топографическая информация |
|
ЦТК |
Цифровая топографическая карта |
|
ЦТП |
Цифровой топографический план |
|
ЦФС |
Цифровая фотограмметрическая система |
|
GPS |
Глобальная навигационная система США (Global Positioning System) |
Предметный указатель
Аналитический фотограмметрический прибор 10, 27 Аэрофотоаппарат 8, 9
Базис глазной 18
- проектирования 53
- фотографирования 52, 85
Высота фотографирования 16
Главная вертикаль 16
Главный оптический луч 15
Деформация иллюминатора 34
- систематическая 38
- случайная 38
Дисторсия абсолютная 36
- радиальная 35
- тангенциальная 36
- фотограмметрическая 36
Идеальный случай аэросъёмки 62
Интервал фотографирования 85
Интерпретоскоп 27
Клинообразность светофильтра 32
Координатные метки 8
Линия неискажённых масштабов 16
- отвесная 16
Маркировка точек на снимке 30
- опознаков 81
Масштаб модели 69 - съёмки 63, 83
Модель геометрическая 69
- стереоскопическая 20
Направляющие косинусы 59
Ортоскопия 35
Острота бинокулярного зрения 19
- монокулярного - 17 Ошибки
- методические 30
- опознавания точек 30
- опорных точек 30
- прибора 30
- снимка 30
- неплоскостности 32
Параллакс поперечный 50,64
- продольный 50,64
- физиологический 18
Параллаксометр 27
Плоскость базисная 68
- главная вертикальная 16, 40
- главная базисная 53
Рабочая площадь снимка 23
- - стереопары 24 Рефракция атмосферная 33
- внутренняя фотограмметрическая 34
Связка проектирующих лучей 10, 49, 69
Сдвиг изображения 43, 86
Система координат объекта 46, 50
- - базисная 53
- - геодезическая 49
- - левого снимка 54
- - планетоцентрическая 51, 132
- - прибора 46
- - сканера 46 - - снимка аналогового 46, 48
- - - цифрового 46
- - полярная 40 Смаз изображения 43
Спектр акустический 12
- электромагнитный 11
Способ измерения мнимой марки 8, 24
- - реальной марки 25
Способ наблюдения стереоэффекта
- - - анаглифический 22
- - - оптический 22
- - - поляроидный 22 - - - растровый 23
- - - чередования снимков 23
Стереокомпаратор 9, 27 Стереопара 20 Стереоскоп 27
Стереоочки 27
Стереоэффект 21
Сферичность планеты 43 Съёмка
аэро- 10, 11 - гидролокационная 12
- кадастровая 138
- космическая 11
- наземная стереофототопографическая 11
- подводная 11
- радиолокационная 12
- рентгеновская 12
- стереофототопографическая 80
Точка
- взаимного ориентирования 92
- главная 16
- контрольная 93
- надира 16
- нулевых искажений 16
- опорная 92
- связующая 93
Точки соответственные 20
Угол наклона аэроснимка 16
- - - поперечный 51 - - - продольный 51
- разворота аэроснимка 51
Фокусное расстояние глаза 17 - - снимка 17
- - фотокамеры 36
Фотограмметрическая засечка
- - двойная 68
- - обратная 68
- - прямая 68
Фототриангуляция блочная 91
- маршрутная 91
Фотосхема многомаршрутная 89
- одномаршрутная 89
- стереоскопическая 90 Фототеодолит 8, 122
Центр проекции 15
Цифровая карта 15
Цифровая модель местности 11 Цифровая фотограмметрическая система 11,
Элементы взаимного ориентирования пары снимков 54
- - - моделей 95
Элементы внешнего ориентирования
- - - модели 74 - - - снимка 51
- - - стереопары 52 Элементы внутреннего ориентирования снимка 49
m'PSf
Краснопевцев Борис Викторович
ФОТОГРАММЕТРИЯ
Учебное пособие по фотограмметрии для студентов 3 курса
специальности "картография"
Оригинал-макет и оформление подготовлены в УПП "Репрография" МИИГАиК
Иллюстрации автора.
Подписано в печать 2008 Гарнитура Таймс.
Формат . Бумага . Печать . Печ. л. . Уч.-изд. л.
Тираж экз. Заказ
УПП "Репрография" МИИГАиК. 105064, Москва, Гороховский пер., 4.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.