Учебные занимательные задания

Марфунина Т.А.

«Занимательные и развивающие задания в начальной школе»

 

   Учебные занимательные задания – задания, непосредственно связанные с программным материалом и способствующие усвоению и закреплению его учащимися.

Учебные задания занимательного характера ценны тем, что они наряду с привитием школьникам интереса к учению способствуют определенному накоплению учебных знаний и навыков, также развивают мышление.

Виды занимательных заданий.

Виды занимательных заданий

Заслуженный учитель России М.Ю.Шуба выделяет следующие виды занимательных заданий:

 

 

 

 

 

 

 

 

 

1.     Занимательные вопросы, задачи, упражнения.

Все компоненты учебной задачи (ее подача, решение, анализ, ответ, выводы) могут быть иногда необычными для учащихся..Поэтому считаем занимательной такую задачу, в которой содержатся элементы занимательности либо в форме подачи задачи, либо в сюжете задачи, либо в способе решения, либо в иллюстративном материале к задаче. Иногда занимательность для учащихся заключается в неожиданности ответа задачи или в выделении элементов игры при решении и т. п..

Занимательные вопросы и задачи.

1.На лугу паслись 16 коров. Их было на 4 меньше, чем овец. Сколько овец паслись на лугу?

2.Таня купила 17 тетрадей в клетку. Это на 9 тетрадей больше, чем в линейку. Сколько тетрадей в линейку купила Таня?

3.Юре подарили столько наклеек, сколько у него уже было. Он пересчитал все наклейки, их оказалось 16. Сколько наклеек было у Юры сначала?

4.В прошлом году Кате было 6 лет. Сколько лет ей будет через 3 года?

5.У Жени, Вики и Насти красный, жёлтый и синий мячи . У Жени не синий и не красный мяч , а у Вики красный мяч. Какого цвета мяч у Насти ? (Синего.)

6.Вова тяжелее Максима, но легче Лёши. Серёжа тяжелее Димы, но легче Вовы. Кто из мальчиков самый тяжёлый?(Лёша.)

7.Два мальчика играли на гитаре , а один –на балалайке. Кто на чём играл , если Артур с Борисом и Борис с Виктором играли на разных инструментах?(Артур и Виктор играли на гитаре , Борис - на балалайке.)

 

2.     Практические работы занимательного характера.

Под практической работой занимательного характера понимаем такую работу, при выполнении которой ученик попадает в необычную ситуацию, где необходимо проявить смекалку, чтобы выполнить поставленное задание. В основном выполнить эту работу надо необычным инструментом или даже вообще без инструментов.

3. Дидактическая игра.

 В игре всегда содержится элемент неожиданности необычности, решается какая-либо задача, проблема, т.е. игра выполняет на занятии (уроке) те же функции, что и занимательная задача. Составляя сценарий какой-либо игры рекомендуется учитывать следующие требования:

- дидактическая игра - это прежде всего урок

- учителю важно хорошо владеть методикой проведения игровых упражнений и игр

- игра должна иметь конкретную тему, цель и задачи;

- при построении игры важно соблюдать цепочку: завязка, развитие действия, кульминация, развязка - финал;

- предоставьте детям относительно большую самостоятельность в игре, если это возможно;

- в основе игры должна лежать деятельность зрителей;

- содержание игры, подбор загадок, конкурсов должны соответствовать возрасту младших школьников;

- следует помнить о времени;

- продумывание оформления игры;

- использование в ходе урока кукол оживляет учебный процесс, снижает у ребят напряжение;

- собирать как особую ценность любимые игры детей;

- новая хорошая игра - лучший подарок детям.

Составим поезд.

Учитель вызывает к доске поочередно учеников. Каждый из них, исполняя роль вагона, называет свой номер. Например, первый вызванный ученик говорит: «Я – первый вагон». Второй ученик, исполняя роль второго вагона, цепляется к первому вагону (кладет левую руку на плече ученика, стоящего впереди), называет свой порядковый номер, остальные составляют пример: «Один да один, получится два». Затем цепляется третий вагон, и все дети по сигналу учителя составляют пример на сложение: «Два да один – это три». И так далее. Потом вагоны (ученики отцепляются по одному, а класс составляет примеры вида: «Три без одного – два. Два без одного – один»). И так далее.

На основе этой игры я предлагаю учащимся сосчитать число вагонов слева направо и справа налево и подвожу их к выводу: считать можно в любом направлении, не пропуская и не считая дважды один предмет.

При изучении нумерации в пределах десяти необходимо довести до понимания детей, что последнее названное при счете число обозначает общее количество всей группы предметов. С этой целью я провожу игры «Хлопки» (хлопать столько раз, сколько выставлено картинок, и показать нужную цифру), «Лучший счетчик», «Посчитаем лепестки у цветка».

При знакомстве с цифрами мы с ребятами обязательно фантазируем, на что похожа изучаемая цифра. И приятно видеть, с какой радостью и увлечением дети работают, и нет границ их фантазий, как горят глаза, и светятся улыбкой лица буквально у всех до одного. А далее дома или в группе продленного дня дети по желанию зарисовывают, на что похожа та или иная цифра.

Характеристика приемов занимательности.

В учебной литературе встречается множество приемов учебной занимательности. Также встречается разбиение их на группы, классы, уровни. Воспользуемся делением, которое предлагает Маслова Г.Г.

Все приемы занимательности  можно разбить на 3 группы:

1.     Приемы занимательности, связанные с подачей задания.

2.     Приемы занимательности, связанные со структурой задания.

3.     Приемы занимательности, связанные с организацией и процессом решения.

Это деление в определенной степени условно. Оно прежде всего нужно для того, чтобы легче было ориентироваться при составлении (подборе) занимательных заданий.

       Занимательные задания способствуют формированию гибкости ума, освобождению мышления от шаблонов.

    « Задания занимательного характера могут служить мостиком от стандартных задач к нестандартным».

     Известно, что учащиеся с трудом решают нестандартные задачи. Причин этому много. Одна из них – резкий переход от стандартных задач к нестандартным. Необходимы переходные задания. Довольно часто ими являются занимательные задачи благодаря их важной особенности: трудности этих задач можно варьировать. Задания, составленные с помощью приемов занимательности («Зашифрованные примеры», «Выбор», «Задумай» и т.д.), освобождены той жесткости, фиксированности, запрограммированности, которая присуща многим учебным заданиям.

          Действительно, учебное задание обычно заранее определяет весь основной ход решения. Для дидактических задач это важно. Однако наряду с ними в обучении надо использовать и задания, которые дают учащимся определенную свободу при их решении. Ведь это же есть не что иное, как творческий подход. Некоторые приемы занимательности («Выбор», «Соответствие», «Задумай» ) прекрасно этому способствуют.

    Таким образом, приемы занимательности часто связаны с общими проблемами обучения: развитием приемов мышления, общеучебных умений и навыков и т.д.

    Значит, кроме прироста математических знаний, умений и навыков, занимательные задания часто выполняют и другие, не менее важные цели: развитие мышления и способностей ученика.

    Возможности использования занимательных заданий на уроках математики.

  Основная задача констатирующего эксперимента заключается в исследовании видов мыслительной деятельности учащихся младшего школьного возраста и умении решать задания с элементами занимательности на уроках математики. В ходе наблюдения за деятельностью учеников, работающих по традиционной системе обучения, было выяснено, что многие из них уже с 1 класса знакомы с занимательными заданиями. Этот факт был учтен авторами новых учебников по математике традиционной системы, которые были изданы в 1998 году. Однако, сделав соотношение учебных заданий с элементами занимательности среди всех учебных заданий в учебниках математики для начальной школы таких авторов, как М.И.Моро, Н.Б.Истоминой, Л.Г.Петерсон, видно, что занимательных заданий в традиционной системе обучения гораздо меньше. Сравнительная характеристика представлена в приложении.

          Для предварительной проверки видов мышления были проведены два теста с целью оценить наглядно-действенное ( «Обведи контур» ) и образно-логическое («Раздели на группы», «Лишний предмет») мышление.

 

Тест «Обведи контур»

Цель: оценить наглядно-действенное мышление.

 Предложить ребенку соединить прямыми линиями фигуры в нижней части рисунка так, как это сделано в верхней части.

   Задача заключается в том, чтобы делать это как можно быстрее и точнее.

Все линии необходимо стараться делать прямыми и точно соединять углы фигур. Желательно также, чтобы контуры фигуры были воспроизведены в тех же самых местах, где они изображены на рисунках-образцах.

   Оцениваются в итоге выполнения задания аккуратность, точность и скорость.

   Если ребенок затратил на выполнение всего задания меньше, чем 100 секунд, если все линии следуют точно по заданным контурам, они прямые и точно соединяют углы - значит, задание выполнено очень хорошо и ребенок имеет высокий уровень развития наглядно-действенного мышления.

 Тест «Раздели на группы»

Цель: оценить образно-логическое мышление.

На рисунке представлены различные геометрические фигуры

   Попросить ребенка внимательно посмотреть на картинку и разделить представленные на ней фигуры на как можно большее число групп. В каждую такую группу могут входить фигуры, выделяемые по одному общему для них признаку. Ребенок называет все фигуры, входящие в каждую из выделенных групп, и тот признак, по которому они выделены.

   На выполнение всего задания отводится 3 минуты.

   Если за это или меньшее время ребенок выделил все группы фигур: треугольники, круги, квадраты, ромбы, фигуры черного цвета, заштрихованные, незаштрихованные, большие фигуры, малые фигуры, - это хороший уровень образно-логического мышления.

Тест «Нелепицы»

Цель: оценить образно-логическое мышление.

  Покажите ребенку картинку, на которой изображены разные нелепицы, и попросите его внимательно рассмотреть эту картинку и сказать, что нарисовано неправильно. Когда ребенок будет называть эти нелепые ситуации, попросите его объяснить, почему это не так и как должно быть на самом деле.

   На все задание отводится не более 2 минут. Если ребенок обнаружит более 8 нелепиц – это хороший результат развития образно-логического мышления.

 

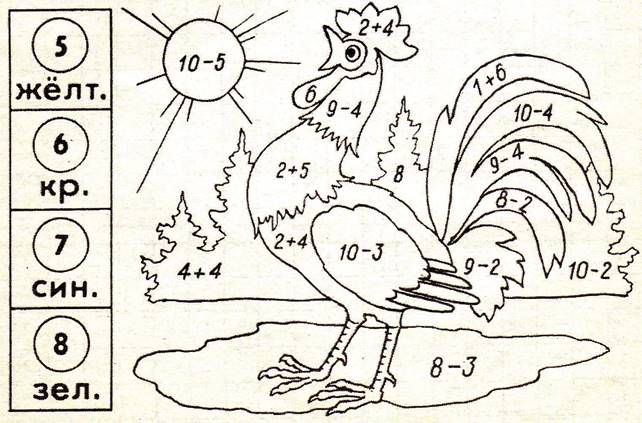
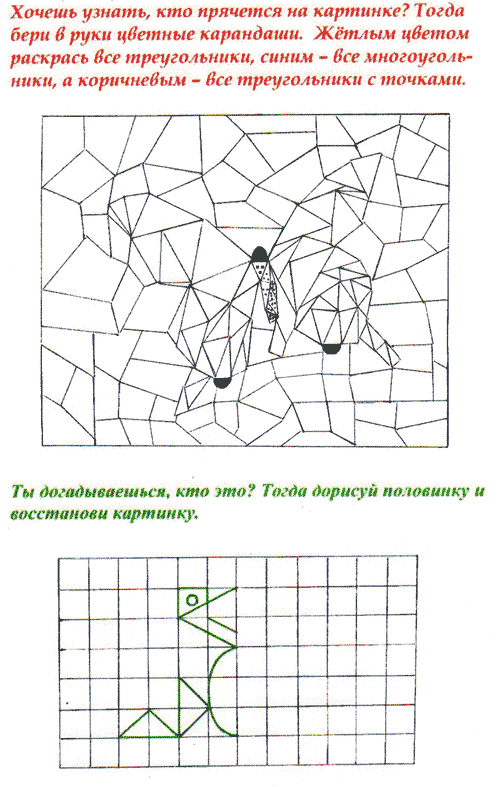
Упражнения на развитие мыслительных операций.

1. Найдите закономерности и продолжите числовой ряд:

·         6, 9, 12, 15, ...

·         2, 7, 3, 8, 4, 9, ...

·         3, 4, 6, 9, 13, ...

·         3, 4, 6, 6, 9, 8, ...

·         1, 1, 2, 3, 5, 8, ...

·         1, 4, 7, 2, 4, 8, 3, 4,...

·         10, 12, 9, 11, 8, 10, ...

·         1, 2, 5, 10, 17, ...

2. Назовите какие-нибудь три признака квадрата, треугольника, прямоугольника.
3. Выделите два слова, наиболее важных для слова перед скобками:

куб (фанера, углы, чертеж, сторона, дерево).

4. Чем схожи и чем отличаются квадрат и равносторонний треугольник?
5. Расположите последовательно в порядке возрастания слова:

месяц, секунда, век, день, минута, сутки, неделя, час, год.

6. Исключите лишнее слово:

квадрат, круг, длина, прямоугольник.

7. Назовите группу слов:

килограмм, сантиметр, градус, минута.

8. Расположите последовательно, следуя образцу

(детская меховая шапка, меховая шапка, шапка, зимний головной убор, головной убор, вещь), слова и словосочетания:

треугольник, фигура, прямоугольный треугольник, геометрическая фигура,  прямоугольный треугольник со стороной 10 см, плоская геометрическая фигура.

9. Даны три слова. Между первым и вторым имеется логическая связь. Подберите четвертое слово, которое связано по смыслу с третьим так же, как первое со вторым, например: береза – дерево; квадрат – ? (четырехугольник).

·         Слагаемые – сумма; множители – ?

·         Прямоугольник – плоскость; куб – ?

·         Слагаемые – сложение; множители – ?

10. Найдите задуманное число, если после того, как к нему прибавили 1, отняли 2, умножили на 3 и разделили на 4, получилось 6.

 

Логические задачки.

Жираф, крокодил и бегемот
жили в разных домиках.
Жираф жил не в красном
и не в синем домике.
Крокодил жил не в красном
и не в оранжевом домике.
Догадайся, в каких домиках жили звери?

2) Три рыбки плавали в разных аквариумах.
Красная рыбка плавала не в круглом
и не в прямоугольном аквариуме.
Золотая рыбка - не в квадратном и не в круглом.
В каком аквариуме плавала зеленая рыбка?

3) Жили-были три девочки:
Таня, Лена и Даша.
Таня выше Лены, Лена выше Даши.
Кто из девочек самая высокая,
а кто самая низкая?
Кого из них как зовут?

 

4)У Миши три тележки разного цвета:
Красная, желтая и синяя.
Еще у Миши три игрушки: неваляшка, пирамидка и юла.
В красной тележке он повезет не юлу и не пирамидку.
В желтой - не юлу и не неваляшку. 
Что повезет Мишка в каждой из тележек?

5) Мышка едет не в первом и не в последнем вагоне. 
Цыпленок не в среднем и не в последнем вагоне. 
В каких вагонах  едут мышка и цыпленок?

Эти простые правила, могут вам помочь:
- наблюдать за ребенком, не вторгаясь в его жизнь и не ограничивая свободу;

- думать, анализировать, рассуждать, ставить, цели, планировать вместе с ребенком;

- прислушиваться к его мнению, советоваться по разным житейским вопросам;

- провоцировать ребенка на мыслительный процесс, постановку осмысленных кратких вопросов, решение проблемных ситуаций;

- устраивать ребенку соревнования с самим собой (его успехи и неудачи сравнивать только с его же успехами и неудачами);

- преодолевать трудности, в том числе учебные, постепенно, начиная с наиболее трудных для ребенка (беспокоит скорость чтения, выразительность);

- хвалить и поощрять ребенка, оценивать и в случае необходимости критиковать только его поступки, а не личность;

- ставить перед ребенком посильные задачи, не оберегать от повседневных дел, не решать за него его проблемы;

- стараться быть для него примером, постоянно анализируя собственные поступки и совершенствуясь как личность;

- стимулировать у ребенка желание и потребность в саморазвитии;

- ребёнок должен выступать в роли деятеля, а не пассивного слушателя.

Желаю вам, проводя развивающие занятия с ребенком, сделать их полезными и приятными.

Список литературы:

1.        Фридман Л.М. Психолого-педагогические основы обучения математики в школе. М.,1983.

2.     Шуба М.Ю. Занимательные задания в обучении математике. М.: Просвещение, 1995.

3.     Тихомирова Л.Ф. Развитие познавательных способностей детей : Популярное пособие для родителей и педагогов. – Ярославль: Академия развития, 1996.

4.     Математика: комплект учебников для 1 – 4 классов /М.И.Моро, М.А.Бантова, Г.В.Бельтюкова и др. – М.: Просвещение, 2000.

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru